頂蓋驅動空腔是計算流體力學（CFD）領域用于驗證計算方法的常用問題之一。雖然涉及的邊界條件相對簡單，但是流動特性卻相當復雜有趣。在本文中，我們將展示如何在 COMSOL Multiphysics? 軟件中定義這一基準問題，并演示映射網格劃分和非線性遞增等適用于多種 CFD 模型的技巧。

在 COMSOL Multiphysics? 中模擬頂蓋驅動空腔

頂蓋驅動空腔包含一個充滿液體的方形空腔。在頂部邊界處，切向速度被用來驅動空腔內的流體流動。剩余的三個壁被定義為無滑移邊界條件，即速度為零。

為了確定基準模型，我們選擇求解那些采用不同方法都能輕松解決的通用性問題。那么，該如何使用描述問題的最通用公式來比較不同的計算方法呢？一種方法是將方程式無量綱化，這意味著問題將不依賴于具體的材料、長度尺度或工作條件。對于頂蓋驅動空腔內流體流動，我們可以求解無量綱納維-斯托克斯方程。

在不包含體積力的情況下，不可壓縮的穩態納維-斯托克斯方程的形式為：

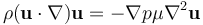
將速度（）、壓力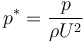（）和長度尺度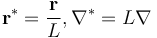（）無量綱化后，可將方程修改為下列形式：

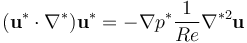
雷諾數的定義是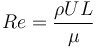。此無量綱參數描述了流體的慣性力相對于粘性力的比重大小。

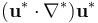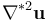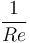通過比較這兩種方程形式，我們可以確定在求解無量綱化方程之前需要在COMSOL Multiphysics 模型中輸入哪些參數。具體來講，既然慣性項前面的系數為 1，因此我們在材料特性中設密度為 1。粘性項的系數是，因此將它作為粘度輸入。

應用非線性遞增

隨著雷諾數增大，與慣性項相比，粘性項在方程中的比重越來越低。由于粘性項在方程中是線性的，而慣性項是非線性的，因此雷諾數的增大使得問題越來越接近非線性。當求解非線性問題時，我們通常選擇利用非線性遞增方法為求解器提供良好的初始條件。下列文章詳細討論了非線性遞增。

黏度遞增方法提高 CFD 模型的收斂性

通過遞增非線性改進非線性問題的收斂

在此模型中，我們在研究中對多個雷諾數進行輔助掃描。這樣做有兩個目的：

將不同雷諾數的解與文獻結果進行比較

演示如何通過采用非線性遞增方法來幫助求解

為了方便收斂，此例中的問題不需要非線性遞增。不過如果處理高度非線性的問題，非線性遞增是改進收斂性的一個重要技巧。

設置邊界條件和約束

至于邊界條件，頂壁朝 x 方向以 U = 1 的速度移動。其他三個壁被施加了無滑移條件（U = 0）。

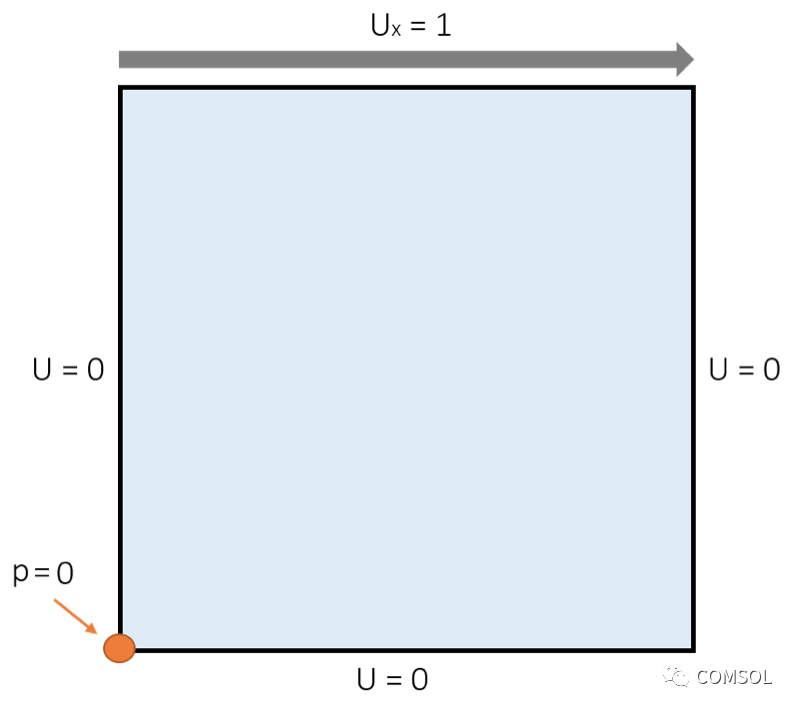
頂蓋驅動空腔模型的邊界條件。

盡管以上邊界條件充分描述了待求解的物理問題，我們還需要對密閉的空腔施加另外一個必要條件：壓力點約束。處于穩態的密閉系統中不存在具有明確壓力水平的入口或出口。缺少了參考壓力，納維-斯托克斯方程對于穩態問題有無數個解，因為它們只能求解隨壓力梯度而變化的問題。因此，壓力點約束規定了流體的絕對壓力水平。當施加 p = 0 的壓力點約束時，這相當于 1 atm 的絕對壓力，介紹如何指定流體壓力的文章就這一點給出了解釋。

只要求解密閉空腔內的穩態流，不管是攪拌釜式反應器還是自然對流問題，一定要在流體內遠離流場關心區域施加壓力點約束。使用壓力點約束的示例模型有水杯中的自然對流和模塊化攪拌器教程。

通過映射網格劃分將域離散化

既然定義好了邊界條件，接下來思考如何將求解域離散化。頂蓋驅動空腔問題是演示如何借助映射網格高效且有效地對四邊形幾何進行離散化的完美示例。映射網格使用矩形單元進行域離散化。我們無需均勻分割這些單元。事實上，我們可以利用網格序列中的映射 節點下的分布 子節點沿邊界定義單元之間的距離。在頂蓋驅動腔體中，我們希望在流動梯度更高的地方，也就是無滑移壁附近堆疊更多單元，這樣就可以在所有邊上施加對稱分布特征。

頂蓋驅動空腔模型的映射網格。

此例中，我們對正方形劃分了映射網格，事實上該技術可應用于任何四邊幾何結構。我們甚至可以將不規則的幾何結構分割成多個四邊實體，從而更方便地劃分映射網格。一些情況下，映射網格比自由三角形網格的計算效率更高，而且更容易控制單元間距。與映射網格相關的案例，請參考平板上方的非等溫湍流和管式反應器中的分解反應教程。

CFD 仿真結果與文獻數據對比

現在我們一起查看結果。首先是采用彩虹色表繪制的空腔內的速度大小，以及利用向量圖指示的流動方向。可以看到，空腔頂部的速度接近于 U = 1，此處的流體流動是由移動壁驅動的。流體被推向右側的壁后，先向下流動，再回到腔體左側。運動在空腔中心產生了一個大型渦流。圖片顯示，當雷諾數較低，例如等于 100 時（左圖），由于粘性項較大而造成的能量損耗，空腔中心的速度較小。雷諾數增加到 10000 后（右圖），空腔內的速度加快，渦流明顯擴展到了空腔底部。

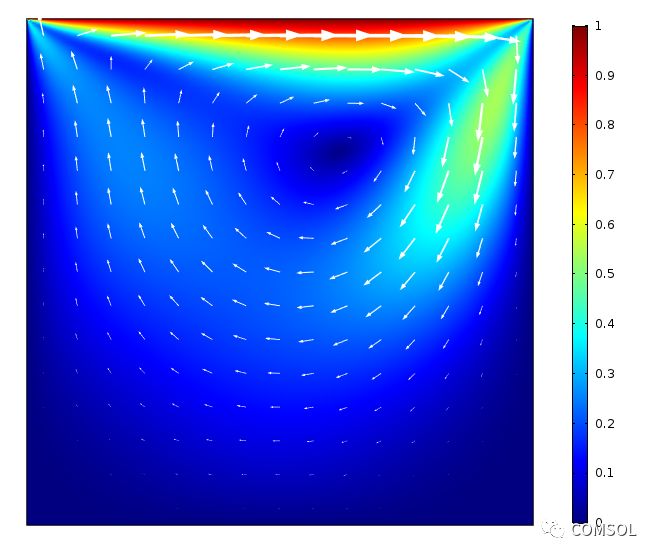
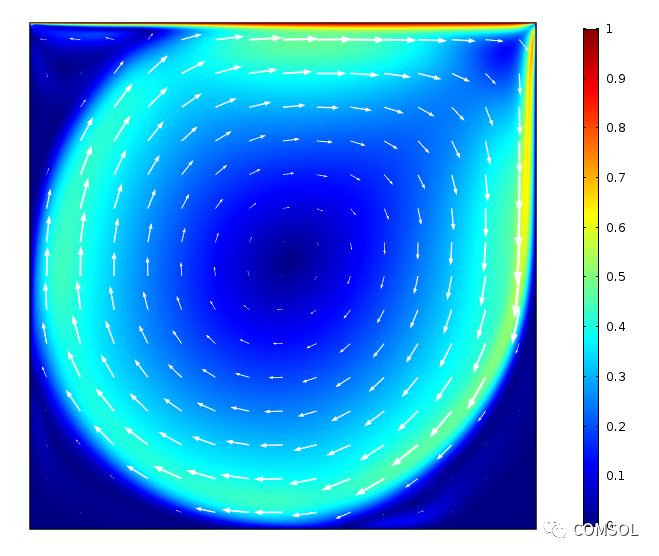
當雷諾數等于 100（左圖）和 1000（右圖）時，空腔內的流體速度和流動方向。

頂蓋驅動腔是一個基準問題，因此我們需要參考現有文獻（Ref. 1）進行比較。首先查看空腔中心線上的速度。下方左圖沿垂直中心線繪制了速度（u）的 x 軸分量，右圖為沿水平中心線的速度（v）的 y 軸分量。在這個雷諾數范圍內，仿真結果與文獻極為一致。

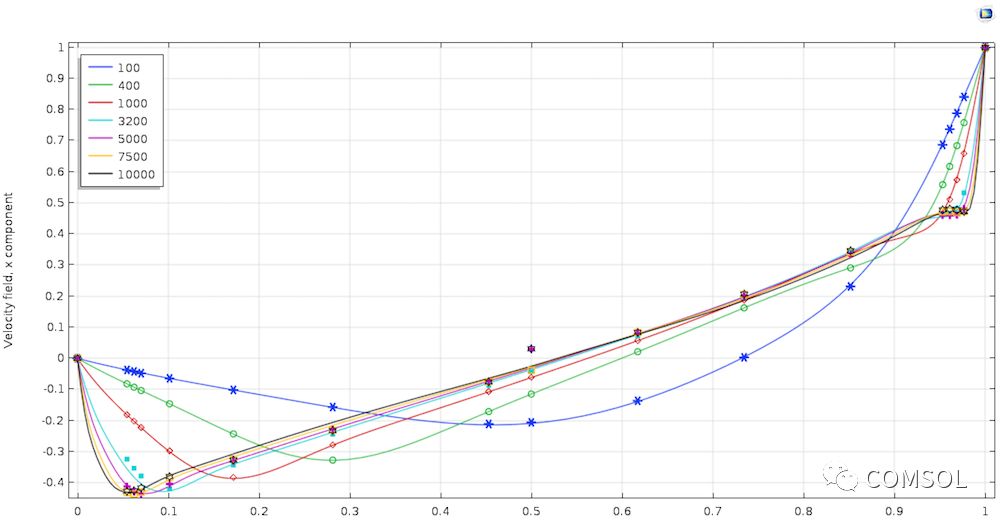
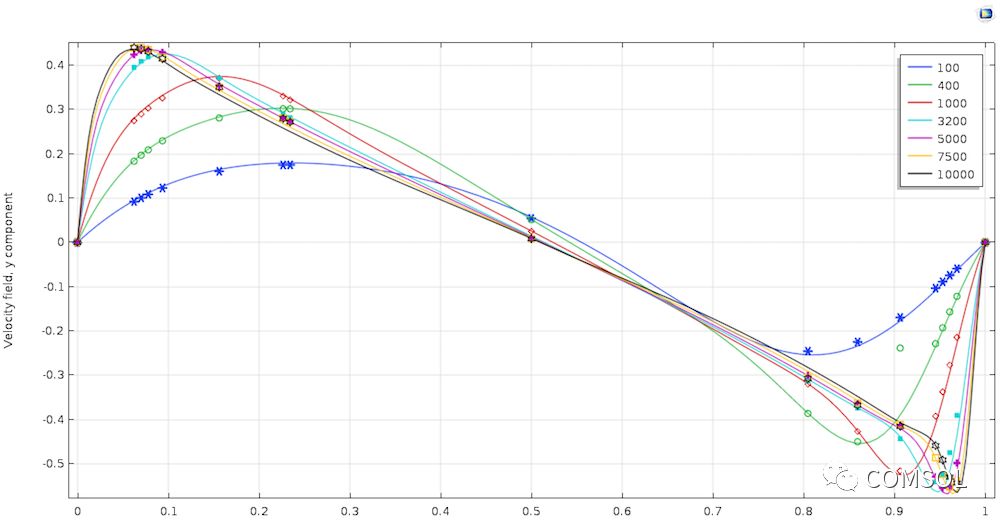
比較仿真結果與文獻中，不同雷諾數下速度的 x 軸分量（左圖）和 y 軸分量（右圖）。

下方的速度繪圖表明大型渦流形成于空腔的中心，但是空腔角落的流動情況又如何呢？我們利用流線繪制了空腔內各個區域的流動結構。由于仿真沒有入口，我們將流線定位 設為均勻密度（而不是在所選邊界上）。

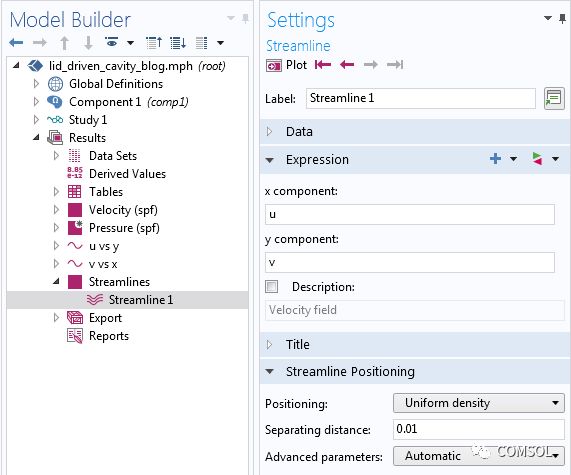
將流線定位設置為均勻密度的設置窗口。

我們可以看到，對于較低的雷諾數，流體在左下角和右下角附近分離，并形成了兩個渦流。隨著雷諾數增大，流體的慣性增強，導致流動更早地與壁分離，并產生了更大的角速度。雷諾數進一步增大后，左上角形成了第三個渦流。對于最大的雷諾數（10000），除了左上角的渦流外，底部兩個角落又產生了兩個渦流。

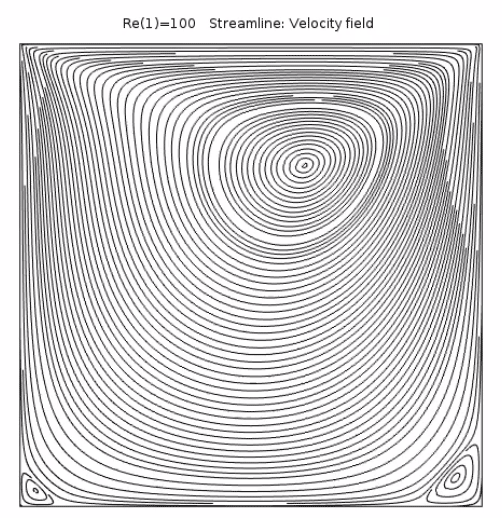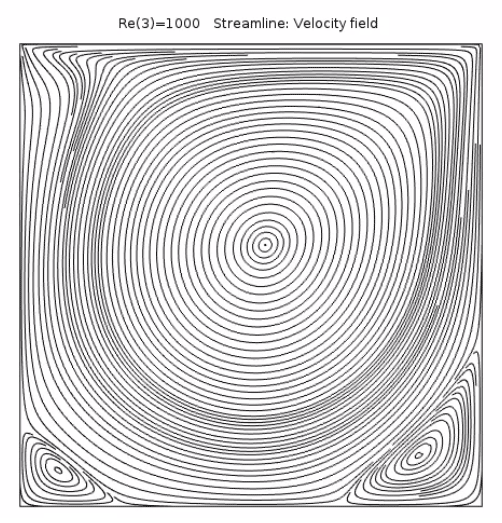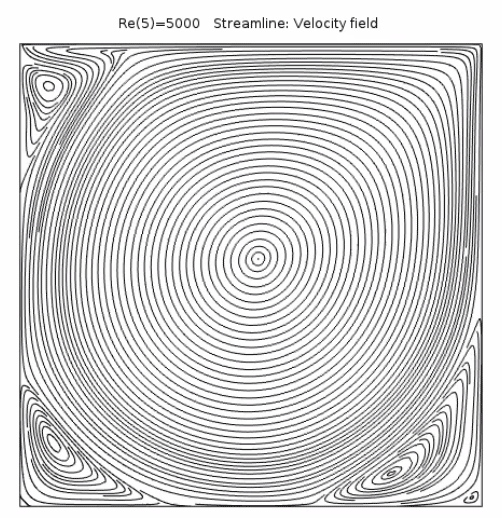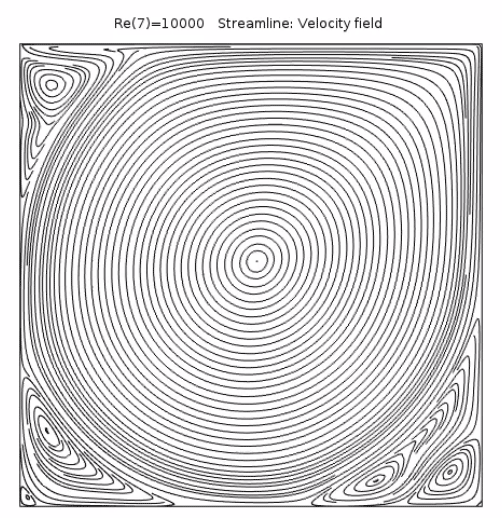
不同雷諾數對應的空腔流動。

頂蓋驅動空腔問題的結語

我們在本文中展示了如何定義經典的 CFD 問題——頂蓋驅動空腔問題。輔助掃描改進了仿真的收斂性，使我們能夠求解多個雷諾數。我們還演示了如何借助映射網格劃分高效地對四邊形幾何離散化，并更好地對壁附近的流體的高梯度進行解析。此外，通過比較仿真結果與現有文獻，我們確定了二者基本相同。