一
簡介
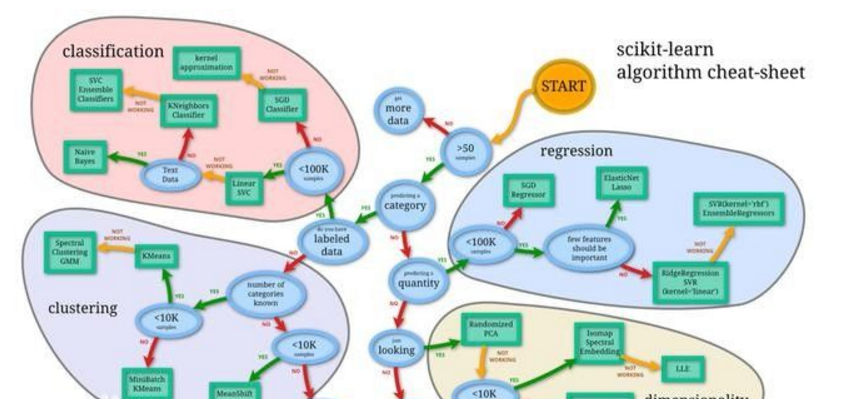
機器學習的知識樹,來源GitHub:

簡單的翻譯一下這個樹:

二
監(jiān)督學習
監(jiān)督學習可以看作是原先的預測模型,有基礎的訓練數(shù)據(jù),再將需要預測的數(shù)據(jù)進行輸入,得到預測的結(jié)果(不管是連續(xù)的還是離散的)
1、決策樹(Decision Tree,DT)
決策樹是一種樹形結(jié)構,為人們提供決策依據(jù),決策樹可以用來回答yes和no問題,它通過樹形結(jié)構將各種情況組合都表示出來,每個分支表示一次選擇(選擇yes還是no),直到所有選擇都進行完畢,最終給出正確答案。
決策樹(decision tree)是一個樹結(jié)構(可以是二叉樹或非二叉樹)。在實際構造決策樹時,通常要進行剪枝,這時為了處理由于數(shù)據(jù)中的噪聲和離群點導致的過分擬合問題。剪枝有兩種:
先剪枝——在構造過程中,當某個節(jié)點滿足剪枝條件,則直接停止此分支的構造。
后剪枝——先構造完成完整的決策樹,再通過某些條件遍歷樹進行剪枝。

2、樸素貝葉斯分類器(Naive Bayesian Model,NBM)
樸素貝葉斯分類器基于貝葉斯定理及其假設(即特征之間是獨立的,是不相互影響的),主要用來解決分類和回歸問題。
具體應用有:
標記一個電子郵件為垃圾郵件或非垃圾郵件;
將新聞文章分為技術類、政治類或體育類;
檢查一段文字表達積極的情緒,或消極的情緒;
用于人臉識別軟件。
學過概率的同學一定都知道貝葉斯定理,這個在250多年前發(fā)明的算法,在信息領域內(nèi)有著無與倫比的地位。貝葉斯分類是一系列分類算法的總稱,這類算法均以貝葉斯定理為基礎,故統(tǒng)稱為貝葉斯分類。樸素貝葉斯算法(Naive Bayesian) 是其中應用最為廣泛的分類算法之一。樸素貝葉斯分類器基于一個簡單的假定:給定目標值時屬性之間相互條件獨立。
3、最小二乘法(Least squares)
你可能聽說過線性回歸。最小均方就是用來求線性回歸的。如下圖所示,平面內(nèi)會有一系列點,然后我們求取一條線,使得這條線盡可能擬合這些點分布,這就是線性回歸。這條線有多種找法,最小二乘法就是其中一種。最小二乘法其原理如下,找到一條線使得平面內(nèi)的所有點到這條線的歐式距離和最小。這條線就是我們要求取得線。

4、邏輯回歸(Logistic Regression)
邏輯回歸模型是一個二分類模型,它選取不同的特征與權重來對樣本進行概率分類,用一個log函數(shù)計算樣本屬于某一類的概率。即一個樣本會有一定的概率屬于一個類,會有一定的概率屬于另一類,概率大的類即為樣本所屬類。用于估計某種事物的可能性。

5、支持向量機(SVM)
支持向量機(support vector machine)是一個二分類算法,它可以在N維空間找到一個(N-1)維的超平面,這個超平面可以將這些點分為兩類。也就是說,平面內(nèi)如果存在線性可分的兩類點,SVM可以找到一條最優(yōu)的直線將這些點分開。SVM應用范圍很廣。

要將兩類分開,想要得到一個超平面,最優(yōu)的超平面是到兩類的margin達到最大,margin就是超平面與離它最近一點的距離,如下圖,Z2>Z1,所以綠色的超平面比較好。

6、K最近鄰算法(KNN,K-NearestNeighbor)
鄰近算法,或者說K最近鄰(KNN,K-NearestNeighbor)分類算法是數(shù)據(jù)挖掘分類技術中最簡單的方法之一。KNN算法的核心思想是如果一個樣本在特征空間中的k個最相鄰的樣本中的大多數(shù)屬于某一個類別,則該樣本也屬于這個類別,并具有這個類別上樣本的特性。該方法在確定分類決策上只依據(jù)最鄰近的一個或者幾個樣本的類別來決定待分樣本所屬的類別。 KNN方法在類別決策時,只與極少量的相鄰樣本有關。由于KNN方法主要靠周圍有限的鄰近的樣本,而不是靠判別類域的方法來確定所屬類別的,因此對于類域的交叉或重疊較多的待分樣本集來說,KNN方法較其他方法更為適合。

主要應用領域是對未知事物的識別,即判斷未知事物屬于哪一類,判斷思想是,基于歐幾里得定理,判斷未知事物的特征和哪一類已知事物的的特征最接近。如上圖,綠色圓要被決定賦予哪個類,是紅色三角形還是藍色四方形?如果K=3,由于紅色三角形所占比例為2/3,綠色圓將被賦予紅色三角形那個類,如果K=5,由于藍色四方形比例為3/5,因此綠色圓被賦予藍色四方形類。由此也說明了KNN算法的結(jié)果很大程度取決于K的選擇。
7、集成學習(Ensemble Learning)
集成學習就是將很多分類器集成在一起,每個分類器有不同的權重,將這些分類器的分類結(jié)果合并在一起,作為最終的分類結(jié)果。最初集成方法為貝葉斯決策。

集成算法用一些相對較弱的學習模型獨立地就同樣的樣本進行訓練,然后把結(jié)果整合起來進行整體預測。集成算法的主要難點在于究竟集成哪些獨立的較弱的學習模型以及如何把學習結(jié)果整合起來。這是一類非常強大的算法,同時也非常流行。
常見的算法包括:
Boosting, Bootstrapped Aggregation(Bagging),
AdaBoost,堆疊泛化(Stacked Generalization, Blending),
梯度推進機(Gradient Boosting Machine, GBM),隨機森林(Random Forest)。
那么集成方法是怎樣工作的,為什么他們會優(yōu)于單個的模型?
他們拉平了輸出偏差:如果你將具有民主黨傾向的民意調(diào)查和具有共和黨傾向的民意調(diào)查取平均,你將得到一個中和的沒有傾向一方的結(jié)果。
它們減小了方差:一堆模型的聚合結(jié)果和單一模型的結(jié)果相比具有更少的噪聲。在金融領域,這被稱為多元化——多只股票的混合投資要比一只股票變化更小。這就是為什么數(shù)據(jù)點越多你的模型會越好,而不是數(shù)據(jù)點越少越好。
它們不太可能產(chǎn)生過擬合:如果你有一個單獨的沒有過擬合的模型,你是用一種簡單的方式(平均,加權平均,邏輯回歸)將這些預測結(jié)果結(jié)合起來,然后就沒有產(chǎn)生過擬合的空間了。
三
無監(jiān)督學習
1、聚類算法
聚類算法就是將一堆數(shù)據(jù)進行處理,根據(jù)它們的相似性對數(shù)據(jù)進行聚類。
聚類,就像回歸一樣,有時候人們描述的是一類問題,有時候描述的是一類算法。聚類算法通常按照中心點或者分層的方式對輸入數(shù)據(jù)進行歸并。所以的聚類算法都試圖找到數(shù)據(jù)的內(nèi)在結(jié)構,以便按照最大的共同點將數(shù)據(jù)進行歸類。常見的聚類算法包括 k-Means算法以及期望最大化算法(Expectation Maximization, EM)。
聚類算法有很多種,具體如下:中心聚類、關聯(lián)聚類、密度聚類、概率聚類、降維、神經(jīng)網(wǎng)絡/深度學習。


2、K-均值算法(K-Means)
K-means算法是硬聚類算法,是典型的基于原型的目標函數(shù)聚類方法的代表,它是數(shù)據(jù)點到原型的某種距離作為優(yōu)化的目標函數(shù),利用函數(shù)求極值的方法得到迭代運算的調(diào)整規(guī)則。K-means算法以歐式距離作為相似度測度,它是求對應某一初始聚類中心向量V最優(yōu)分類,使得評價指標J最小。算法采用誤差平方和準則函數(shù)作為聚類準則函數(shù)。K-means算法是很典型的基于距離的聚類算法,采用距離作為相似性的評價指標,即認為兩個對象的距離越近,其相似度就越大。該算法認為簇是由距離靠近的對象組成的,因此把得到緊湊且獨立的簇作為最終目標。

通常,人們根據(jù)樣本間的某種距離或者相似性來定義聚類,即把相似的(或距離近的)樣本聚為同一類,而把不相似的(或距離遠的)樣本歸在其他類。
3、主成分分析(Principal Component Analysis,PCA)
主成分分析是利用正交變換將一些列可能相關數(shù)據(jù)轉(zhuǎn)換為線性無關數(shù)據(jù),從而找到主成分。PCA方法最著名的應用應該是在人臉識別中特征提取及數(shù)據(jù)降維。

PCA主要用于簡單學習與可視化中數(shù)據(jù)壓縮、簡化。但是PCA有一定的局限性,它需要你擁有特定領域的相關知識。對噪音比較多的數(shù)據(jù)并不適用。
4、SVD矩陣分解(Singular Value Decomposition)
也叫奇異值分解(Singular Value Decomposition),是線性代數(shù)中一種重要的矩陣分解,是矩陣分析中正規(guī)矩陣酉對角化的推廣。在信號處理、統(tǒng)計學等領域有重要應用。SVD矩陣是一個復雜的實復負數(shù)矩陣,給定一個m行、n列的矩陣M,那么M矩陣可以分解為M = UΣV。U和V是酉矩陣,Σ為對角陣。

PCA實際上就是一個簡化版本的SVD分解。在計算機視覺領域,第一個臉部識別算法就是基于PCA與SVD的,用特征對臉部進行特征表示,然后降維、最后進行面部匹配。盡管現(xiàn)在面部識別方法復雜,但是基本原理還是類似的。
5、獨立成分分析(ICA)
獨立成分分析(Independent Component Analysis,ICA)是一門統(tǒng)計技術,用于發(fā)現(xiàn)存在于隨機變量下的隱性因素。ICA為給觀測數(shù)據(jù)定義了一個生成模型。在這個模型中,其認為數(shù)據(jù)變量是由隱性變量,經(jīng)一個混合系統(tǒng)線性混合而成,這個混合系統(tǒng)未知。并且假設潛在因素屬于非高斯分布、并且相互獨立,稱之為可觀測數(shù)據(jù)的獨立成分。

ICA與PCA相關,但它在發(fā)現(xiàn)潛在因素方面效果良好。它可以應用在數(shù)字圖像、檔文數(shù)據(jù)庫、經(jīng)濟指標、心里測量等。

上圖為基于ICA的人臉識別模型。實際上這些機器學習算法并不是全都像想象中一樣復雜,有些還和高中數(shù)學緊密相關。
四
強化學習
1、Q-Learning算法
Q-learning要解決的是這樣的問題:一個能感知環(huán)境的自治agent,怎樣通過學習選擇能達到其目標的最優(yōu)動作。
強化學習目的是構造一個控制策略,使得Agent行為性能達到最大。Agent從復雜的環(huán)境中感知信息,對信息進行處理。Agent通過學習改進自身的性能并選擇行為,從而產(chǎn)生群體行為的選擇,個體行為選擇和群體行為選擇使得Agent作出決策選擇某一動作,進而影響環(huán)境。增強學習是指從動物學習、隨機逼近和優(yōu)化控制等理論發(fā)展而來,是一種無導師在線學習技術,從環(huán)境狀態(tài)到動作映射學習,使得Agent根據(jù)最大獎勵值采取最優(yōu)的策略;Agent感知環(huán)境中的狀態(tài)信息,搜索策略(哪種策略可以產(chǎn)生最有效的學習)選擇最優(yōu)的動作,從而引起狀態(tài)的改變并得到一個延遲回報值,更新評估函數(shù),完成一次學習過程后,進入下一輪的學習訓練,重復循環(huán)迭代,直到滿足整個學習的條件,終止學習。
Q-Learning是一種無模型的強化學習技術。具體來說,可以使用Q學習來為任何給定的(有限的)馬爾可夫決策過程(MDP)找到最優(yōu)的動作選擇策略。它通過學習一個動作價值函數(shù),最終給出在給定狀態(tài)下采取給定動作的預期效用,然后遵循最優(yōu)策略。一個策略是代理在選擇動作后遵循的規(guī)則。當這種動作值函數(shù)被學習時,可以通過簡單地選擇每個狀態(tài)中具有最高值的動作來構建最優(yōu)策略。 Q-learning的優(yōu)點之一是能夠比較可用操作的預期效用,而不需要環(huán)境模型。此外,Q學習可以處理隨機過渡和獎勵的問題,而不需要任何適應。已經(jīng)證明,對于任何有限的MDP,Q學習最終找到一個最優(yōu)策略,從總體獎勵的預期值返回到從當前狀態(tài)開始的所有連續(xù)步驟是最大可實現(xiàn)的意義。
-
人工智能
+關注
關注
1793文章
47539瀏覽量
239392 -
機器學習
+關注
關注
66文章
8434瀏覽量
132866
原文標題:機器學習常用算法總結(jié)
文章出處:【微信號:gh_c472c2199c88,微信公眾號:嵌入式微處理器】歡迎添加關注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關推薦




 淺析機器學習常用的算法
淺析機器學習常用的算法











評論