COMSOL Multiphysics? 軟件“聲學模塊”中的基于邊界元方法(boundary element method,簡稱 BEM)建模物理場接口可以和基于有限元方法(finite element method,簡稱 FEM)的接口無縫耦合,從而對聲-結構相互作用等問題進行建模。本文介紹了邊界元法的功能、案例與相關的后處理技巧。
基于邊界元方法進行聲學建模優勢
“聲學模塊”的壓力聲學,邊界元 接口提供了 BEM 功能。該接口適用于求解每個域內的材料屬性均為恒定值的二維和三維聲學問題。通過采用復值材料屬性,用戶可以在流體模型中引入損耗。此外,邊界元接口還可以進行散射場仿真,也就是說它能夠處理散射問題(見下圖)。借助新的邊界元法,用戶能夠求解以前不支持的問題類型,下文將進行詳述。
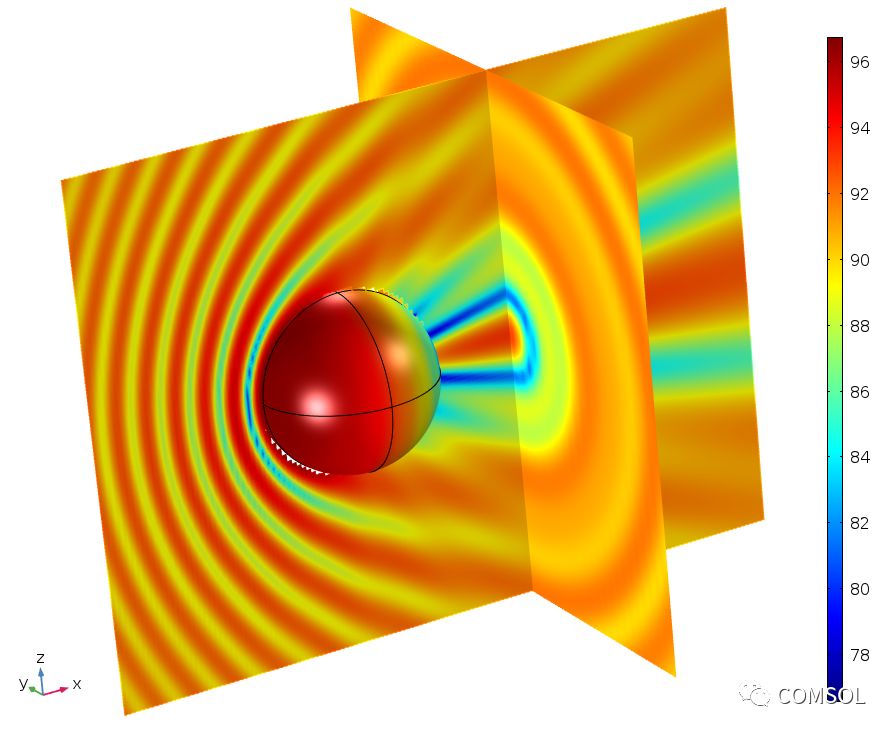
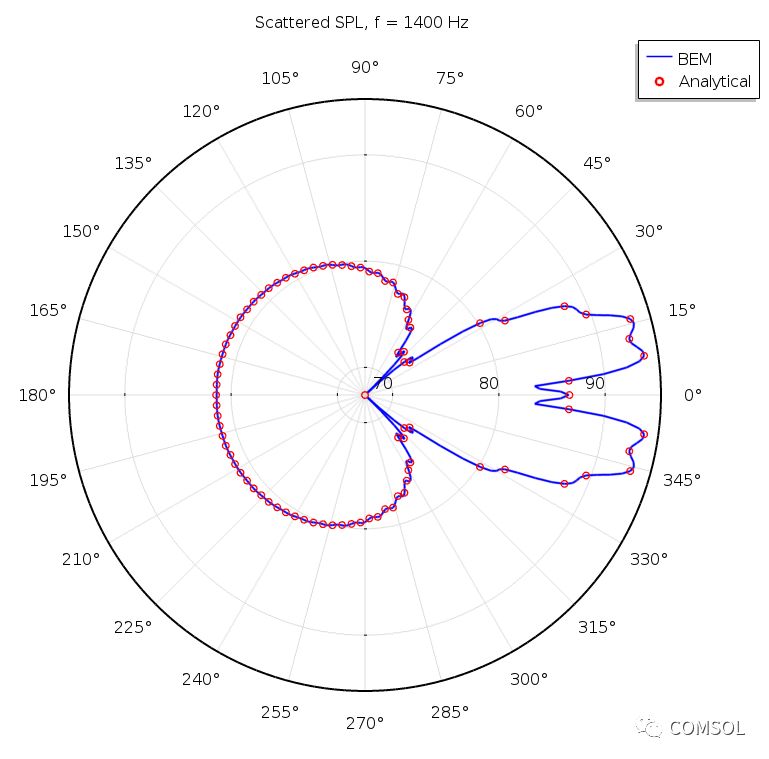
球形散射體的經典 BEM 基準模型,圖片比較了模型結果與解析解。上圖顯示 500 Hz 頻率下兩個截面的聲壓級,下方的對比圖顯示了 1400 Hz 頻率下的散射場。圖片來自球形散射體:BEM 基準教學模型。
將基于 BEM 和 FEM 的接口相互耦合是軟件的一項重要功能。例如,利用聲-結構邊界 多物理場耦合將聲學 BEM 接口與基于 FEM 的振動結構相互耦合;通過聲學 BEM-FEM 邊界 多物理場耦合使 BEM 和 FEM 聲學域相結合。
出色的靈活性使得用戶可將 BEM 和 FEM 應用到最合適的場景中,而且與 COMSOL Multiphysics 的所有其他物理場耦合一樣,所有操作均在一個用戶界面中完成。舉例來說,FEM 可以添加更通用的材料屬性,因此適合模擬振動結構的內部域,比如封閉的空氣域;外部域則使用 BEM,因為它更適合對大型域和無限域建模。下圖中的揚聲器模型采用了兩種方法。
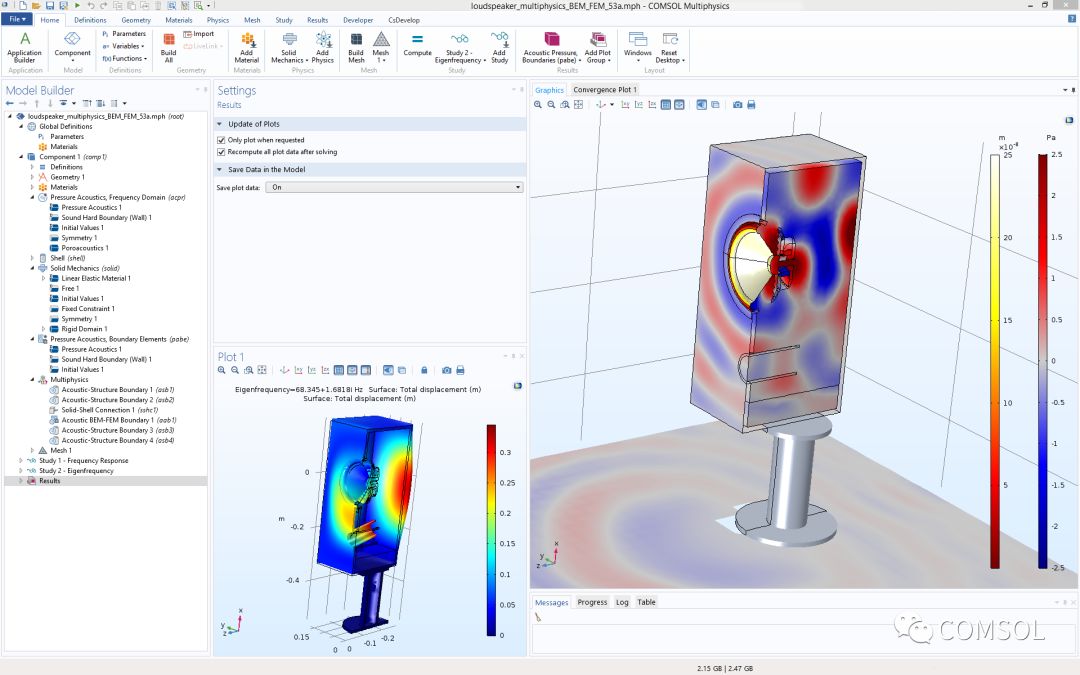
揚聲器多物理場模型的 COMSOL Multiphysics 用戶界面,模型包含 BEM 和 FEM 聲學以及 固體力學和 殼接口。物理場被耦合到內置的多物理場耦合中。圖片來自振動聲學揚聲器仿真:基于混合 BEM-FEM 法的多物理場教學模型。
利用邊界元法,我們只需對鄰近建模域的表面劃分網格。這意味著不需要對大型體積進行網格劃分(有限元法則不然),因此基于 BEM 的接口尤其適用于涉及輻射和散射,且擁有詳細 CAD 幾何的模型。該接口還提供了內置條件,供用戶設置無限硬聲場邊界(壁)或無限軟聲場邊界。這些邊界條件對建模十分有利,例如在水下聲學問題中,無限軟聲場邊界可用于模擬海洋表面。
對于包含大型流體域的問題,基于 BEM 的接口通常更具優勢,若使用 FEM,就必須創建對大型體積進行網格劃分,而較大的三維網格會導致內存溢出。針對類似情況,邊界元法甚至能夠拓寬 COMSOL Multiphysics 可處理的問題類型。這些問題的一些相關示例包括:
無限壁或無限軟聲場邊界與輻射對象相距很遠(就波長而言)的模型
散射對象和輻射對象相距很遠且發生相互作用的模型
復雜非緊湊幾何的輻射問題,對此類問題使用 FEM 時,很難施加合適的輻射條件或完美匹配層(perfectly matched layer,簡稱 PML)
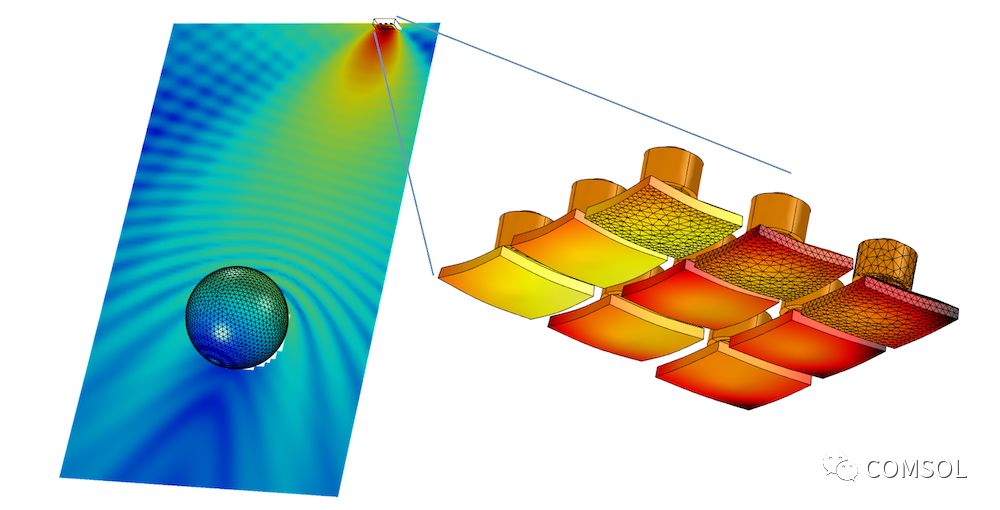
與散射對象相距很遠的換能器陣列的示例圖。由于內存需求很大,這種問題很難或者不可能單純利用有限元法來求解。邊界元法適用于求解此類模型(將球體移動到遠處不會增加計算量)。圖片來自聲納系統的蘑菇形換能器陣列教學模型。
針對相同數量的自由度(degrees of freedom,簡稱 DOF),邊界元法對計算能力的要求比有限元法更高,但另一方面,要獲得相同的精度,邊界元法要求的自由度一般比有限元法少得多。BEM 可生成完全填充且密集的系統矩陣,因此它需要使用與 FEM 不同的專用數值方法。在求解小型和中型聲學模型時,基于 FEM 的接口——例如壓力聲學,頻域 接口——的速度通常比 BEM 更快。
根據“聲學模塊”的用戶指南,壓力聲學,邊界元 接口的邊界元法是基于一種利用 Costabel 對稱耦合的直接方法。為了對所得的線性系統進行求解,我們利用了自適應交叉近似(ACA)快速求和算法。該方法使用了部分裝配矩陣,該處矩陣與向量相乘的效果得以計算。缺省迭代求解器為 GMRES。內置的多物理場耦合降低了無縫創建混合 FEM 和 BEM 物理場問題的難度。在求解耦合模型時,對 BEM 問題采用默認的 ACA 混合算法,對 FEM 使用合適的預條件器(直接或多重網格)。
兩全其美的方法:混合 FEM-BEM 法
如上文所述,壓力聲學,邊界元 接口可與基于有限元的接口中無縫耦合,比如壓力聲學,頻域 接口和固體力學 接口。借助耦合,創建混合 FEM-BEM 模型變得很輕松,而且模型能夠在最需要和最合適的地方充分利用方程各自的優勢。
BEM 不等于替代聲場中的有限元,而應該看作一種補充。按照經驗,由于基于 FEM 的模型在求解時需要非常細化的網格,所以大型流體域應該選擇 BEM,或者將基于 BEM 與 FEM 的物理場耦合到一起。下面是一些應用和示例:
模擬具有復雜幾何的換能器和輻射問題
利用 FEM 模擬(壓電式或電磁式)換能器,與此同時利用 BEM 模擬外聲場
耦合內部和外部問題
對狹窄區域和共振體使用 FEM,對輻射區域使用 BEM
請牢記:聲學 BEM-FEM邊界 多物理場耦合可以幫助用戶輕松耦合基于 BEM 和 FEM 的聲學模型
對于內存足夠的較小模型,有限元法通常更快。利用輻射條件或 PML的傳統方法適合模擬開放的輻射域。
壓力聲學,邊界元 接口可用于替代基于 FEM 的輻射條件/PML 以及遠場計算特征。參見下圖中的模型示例。
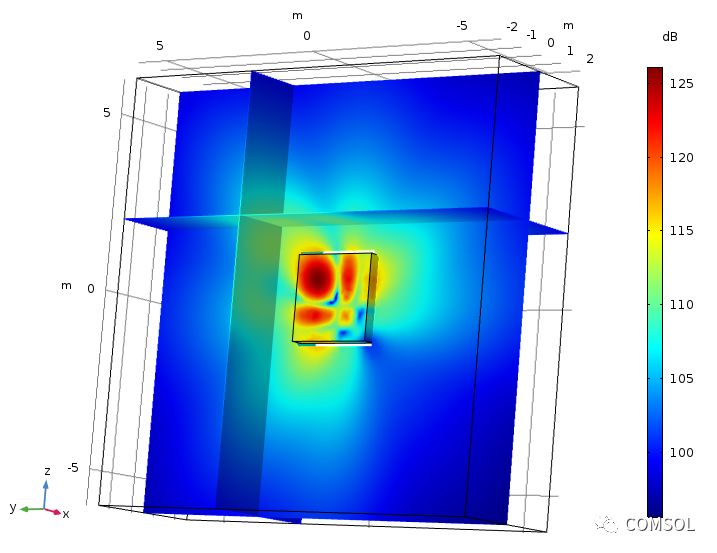
在貝塞爾面板教學模型中,壓力聲學,邊界元口被用來模擬開放空間。邊界元接口可以有效地替代原本需要的輻射條件(或 PML)和遠場計算特征。圖片展示了 FEM 域(多個點源位于該域內)內的表面聲壓級,以及外部 BEM 域在特定范圍內的三個截面的聲壓級。
BEM 模型的后處理
當使用 BEM 接口求解問題時,所得的解由邊界上的因變量——相當于未知場變量——組成,其中包括壓力 p 及其法向導數;也就是法向通量變量 pabe.pbam1.bemflux。域內的解是以計算積分內核為基礎的,這是 BEM 的核心。
邊界上定義了專用的邊界變量。該變量在外部和內部邊界上擁有不同定義;在外部邊界上,它等于因變量。在內部邊界上,則被定義為向上和向下壓力相關變量(pabe.p_up 和 pabe.p_down),因為此處壓力是不連續的;比如內部硬聲場壁 邊界。此外,所有邊界上都有預定義后處理變量,必要時,這些變量能夠將邊界變量與基于內核計算的變量的屬性組合在一起。
如下圖所示,我們可以在繪圖的替換表達式 列表中找到上述變量以及所有其他后處理變量。
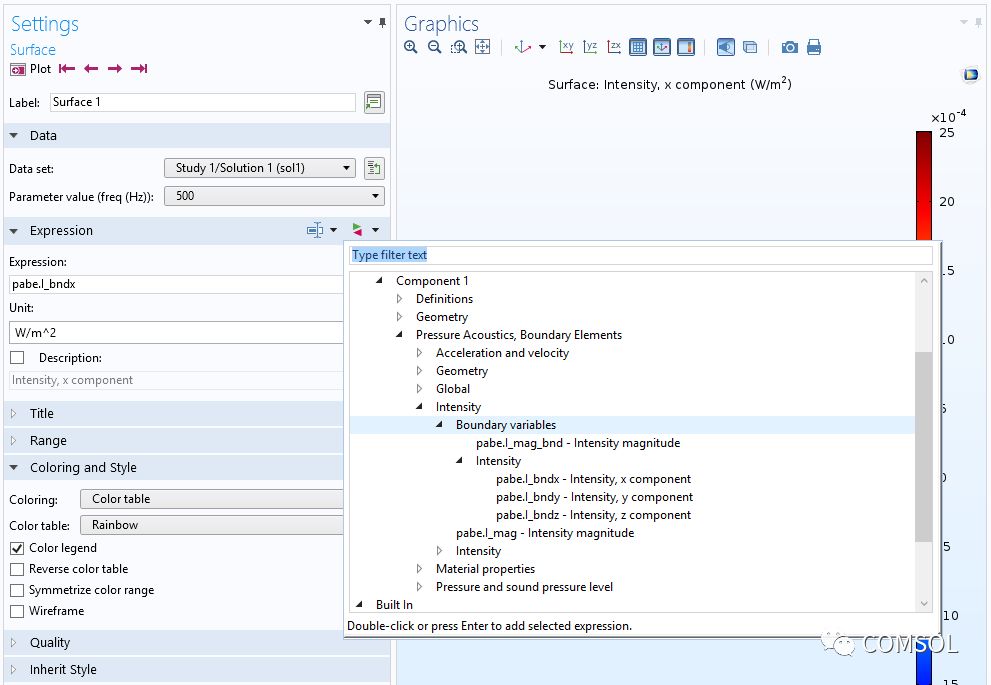
用戶界面截圖顯示了一部分預定義后處理變量的列表。
在域內對 BEM 解進行后處理時,必須使用上文提到的 BEM 積分內核計算來重構壓力場。為了使 BEM 解更易于可視化,我們可以在柵格上自動執行內核計算,從而生成專用的數據集。下面幾段討論了可用于繪制聲學結果的數據集。
三維柵格 和二維柵格 數據集專門求解沒有網格的域。這些數據集在待求解的區域建立了由點組成的規則柵格。柵格的尺寸和邊界以及解析度(柵格間距)均可修改。對波動問題進行可視化時,充足的空間解析度非常重要。然而,解析度不應過大,否則會增加渲染時間。
柵格數據集還有其他用途,例如用作切面圖或表面圖的輸入數據集。在求解 BEM 模型時,系統會自動生成柵格數據集和多切面圖,并將其應用到默認的繪圖中。柵格數據集還能用作截面、截線或者截點的輸入。
只要勾選僅計算全局定義的表達式 選項,就可以直接利用參數化曲線和表面計算 BEM 的解。
BEM 變量被用作輸入時,我們可以直接使用專門的聲學繪圖。相關示例包括用于繪制空間響應的遠場 圖(不一定是遠場,實際上可以是任何距離)以及方向性 圖。舉例來說,聲壓級變量 pabe.Lp 可以用作表達式。
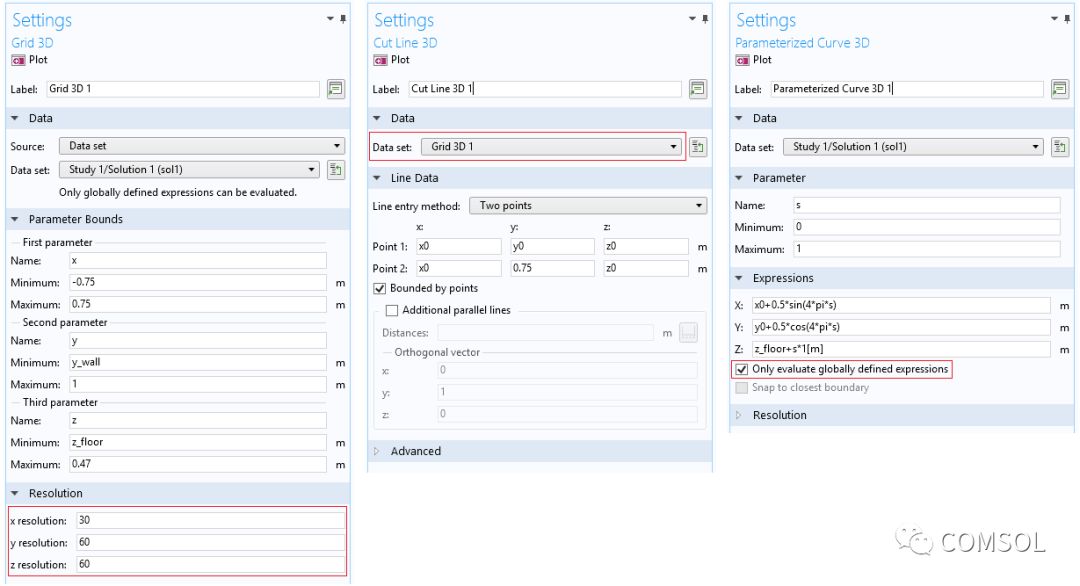
用戶界面截圖顯示了上文提及的一些不同的數據集。重要設置已突出顯示。
上方截圖摘自揚聲器輻射:BEM 聲學教學模型。該模型求解輻射問題,并且創建了多數常見繪圖和結果可視化效果。
下圖顯示了利用揚聲器表面的柵格繪制在三個切面上的聲壓級。為了表現后處理與可視化工具的通用性,圖片還沿著使用參數化曲線 三維數據集創建的參數化螺旋曲線繪制了聲壓級結果。
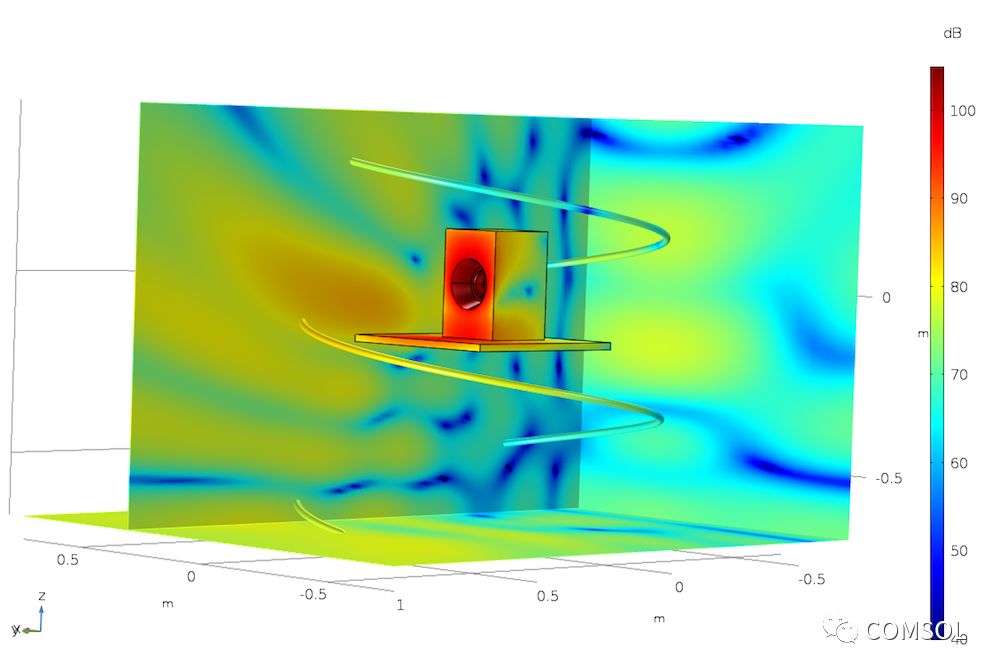
“揚聲器輻射:BEM 聲學”教學模型以多種方式顯示聲壓級結果。
使用邊界元法的兩種特殊情況
接下來,我們將討論使用邊界元法時兩種需要特別考慮的情況。
第 1 種情況:半空間輻射問題
很多聲學應用都涉及了一種情況:換能器位于一個無限擋板內,并朝向半空間輻射。大多數情況下,此類裝置不能使用 BEM,至少在包含無限擋板的情況下絕對不行。非無限擋板可以使用內部硬聲場壁 等邊界條件來創建。
我們通常習慣使用無限硬聲場邊界 特征。該邊界條件不能用于像揚聲器驅動器立著的擋板那樣“中間有一個洞”的邊界。因為 BEM 方程基于全空間格林函數,所以無限對稱平面或無限壁條件意味著平面或壁必須無限延伸,而且不能有開口。基本上,如果邊界在物理場接口中擁有對應的選擇,且選擇處于活動狀態,那么這些邊界必須位于無限邊界條件的同一側或者位于無限邊界條件上。否則將產生非物理結果。
針對如何設置無限擋板,我的一般建議是將基于 FEM 的物理場接口同遠場計算特征及 PML 或輻射條件結合使用。揚聲器驅動器的集總模型就是一個例子。這種設置通常快得多!
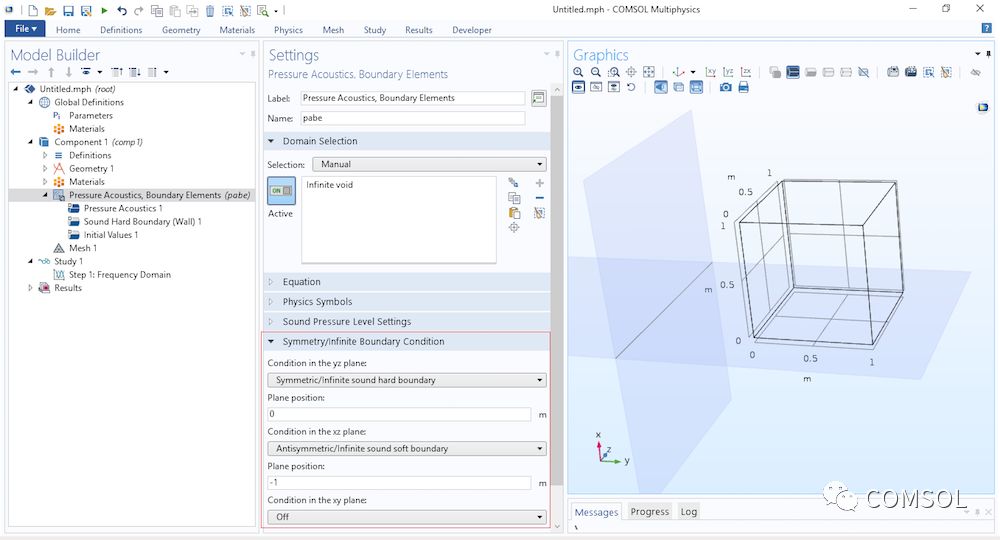
壓力聲學,邊界元接口的用戶界面。物理場頂層設置了無限邊界條件(突出顯示)。選定任意條件后,生成的平面將顯示在“圖形窗口”中。
第 2 種情況:內邊值問題
內邊值問題——特別是沒有或產生很少損耗的銳共振問題——很難使用 BEM進行求解。問題的原因不在于方法本身,而是因為使用了迭代求解器來高效求解底層矩陣系統。基于 FEM 的模型使用迭代求解器時也會出現相同的問題。
在靠近銳共振的地方,任何細微的變化都會導致壓力變化,但是我們很難捕捉這種變化來確保收斂。如果可能的話,遇到這些情況時,建議結合使用 FEM 和直接求解器,或者添加真實的帶損耗的邊界條件,例如阻抗條件。
關于 BEM 的結語
在 COMSOL Multiphysics 軟件環境中,BEM 是對 FEM 的實用補充。眾多從事聲學建模的工程師都期望著增加這項功能。我們希望你會喜歡“聲學模塊”的這項新增功能。
下一步操作
點擊下方按鈕,探索附加的“聲學模塊”產品提供的專業聲學建模功能還可以實現哪些應用。
親自動手操作:下載本文中的教學模型。訪問“案例下載”頁面,登錄 COMSOL Access 賬號后即可下載 MPH 文件。
球形散射體:BEM 基準
聲吶系統的蘑菇形換能器陣列
振動聲學揚聲器仿真:基于混合 BEM-FEM 法的多物理場
貝塞爾面板
揚聲器輻射:BEM 聲學教程
-
揚聲器
+關注
關注
29文章
1307瀏覽量
63080 -
網格
+關注
關注
0文章
139瀏覽量
16024 -
邊界元法
+關注
關注
1文章
2瀏覽量
1386
原文標題:如何利用邊界元方法進行聲學建模
文章出處:【微信號:COMSOL-China,微信公眾號:COMSOL】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
在Multisim的仿真分析中后處理器應該如何使用?
具有專利的運動精確圖像視頻后處理器
有限元法的原理
基于邊界元的非連續(塊體系統)形變反分析法
解析PCB電鍍后處理的12類處理方法工藝
使用Python的焊接后處理的詳細說明

為大家帶來后處理尿素泵針腳定義總結
康明斯后處理1柴油機排氣處理液噴射溫度傳感器
出保的車后處理有問題該怎么辦?
OFDR傳感解調過程和OSI后處理功能的介紹
Mastercam后處理機器定義說明
OFDR傳感解調過程和OSI后處理功能的介紹





 邊界元法的功能、案例與相關的后處理技巧
邊界元法的功能、案例與相關的后處理技巧












評論