公歷 3 月 12 日是一年一度的植樹節。旨在宣傳保護森林,并動員群眾參加植樹造林活動。說到樹,程序猿們肯定不陌生,趁著這個植樹節,普及一下程序猿們經常遇見的樹。
二叉搜索樹
定義
二叉搜索樹又稱二叉查找樹,亦稱為二叉排序樹。設 x 為二叉查找樹中的一個節點,x 節點包含關鍵字 key,節點x 的 key 值記為 key[x] 。如果 y 是 x 的左子樹中的一個節點,則 key[y] <= key[x] ;如果 y 是 x 的右子樹的一個節點,則 key[y] >= key[x] 。
查找性能
當數據數目為 N,樹高度保持 logN 附近。則平均查找長度與 logN 成正比,查找平均時間復雜度為 O(logN) 。 當先后插入的關鍵字有序時,二叉搜索樹退化成單支樹結構。此時樹高 N 。平均查找長度為 (N+1)/2 ,查找的平均時間復雜度為 O(N) 。
插入性能
插入效率與查找效率一致。??
刪除性能
刪除節點時,若節點為葉子節點,或者節點只有單一子樹,則時間復雜度為 O(1) 。若節點既有左子樹又有右子樹,則需要執行遞歸過程,對應時間復雜度為 O(logN) 。
應用場景
二叉排序樹就既有鏈表的好處,也有數組的好處,因此在處理大批量的動態的數據是比較有用。
種樹
平衡二叉樹
定義
平衡二叉樹是一種特殊的二叉搜索樹。平衡二叉樹保證節點平衡因子的絕對值不超過1,保證了樹的平衡。
查找性能
平衡二叉樹是嚴格平衡的,那么查找過程與二叉搜索樹一樣,只是平衡二叉樹不會出現最差的單支樹情形。因此查找效率最好,最壞情況時間復雜度為 O(logN) 。
插入性能
插入數據之前需要進行查找操作,查找到插入位置。插入數據后需要進行旋轉操作,旋轉操作復雜度為常量級。因此插入數據的時間復雜度與查找相同為 O(logN)。
刪除性能
刪除數據同樣需要查找數據,在刪除數據后需要進行調整。一次刪除最多需要需要O(logN)次旋轉,因此刪除數據的時間復雜度為O(logN)+O(logN)=O(2logN)。
應用場景
SGI/STL的 set/map 底層都是用紅黑樹(平衡二叉樹的一種)實現的。
種樹
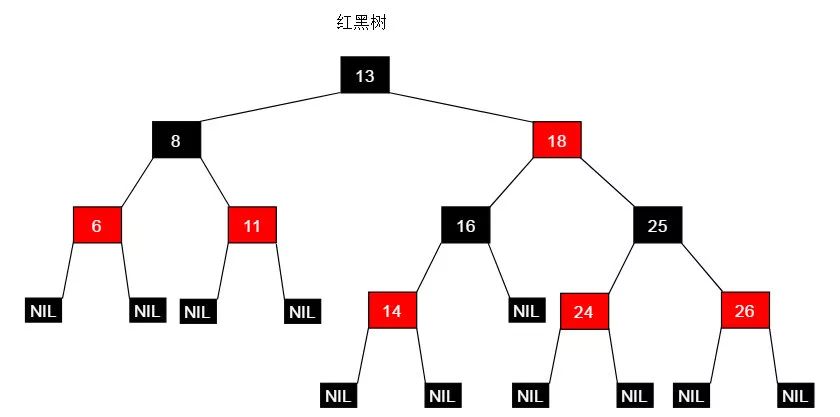
紅黑樹
定義
平衡二叉樹的嚴格平衡策略以犧牲建立查找結構(插入,刪除操作)的代價,換來了穩定的O(logN) 的查找時間復雜度。紅黑樹采用了折中策略,即不犧牲太大的建立查找結構的代價,同時又能保證穩定高效的查找效率。
查找性能
由于紅黑樹的性質(最長路徑長度不超過最短路徑長度的 2 倍),可以說明紅黑樹雖然不像平衡二叉樹一樣是嚴格平衡的,但平衡性能還是要比二叉搜索樹要好。其查找代價基本維持在 O(logN) 左右,但在最差情況下(最長路徑是最短路徑的 2 倍少 1),比平衡二叉樹效率低一些。
插入性能
紅黑樹插入結點時,需要旋轉操作和變色操作。但由于只需要保證紅黑樹基本平衡就可以了。因此插入結點最多只需要2次旋轉,這一點和平衡二叉樹的插入操作一樣,但是變色操作的時間復雜度為O(logN)。
刪除性能
紅黑樹的刪除操作代價要比平衡二叉樹要好的多,刪除一個結點最多只需要 3 次旋轉操作,保證了刪除時間復雜度維持在常量級。
應用場景
應用場景有很多。
Java 中的 TreeSet ,TreeMap,HashMap
C++ 的 STL中的 map 和 set 都是用紅黑樹實現的
epoll 在內核中的實現,用紅黑樹管理事件塊
nginx 中,用紅黑樹管理 timer 等
linux 進程調度 Completely Fair Schedule r,用紅黑樹管理進程控制塊
種樹
B 樹
定義
B樹是一種多路平衡查找樹,在相同數據數目情形下,B樹的高度更小,這樣就減少了磁盤的IO次數,在文件系統以及數據庫索引等場景下提升了查找效率。
查找性能
B樹的查找分成兩種:一種是從一個結點查找另一結點的地址的時候,需要定位磁盤地址(查找地址),查找代價極高。另一種是將結點中的有序關鍵字序列放入內存,進行優化查找(可以用折半),相比查找代價極低。而B樹的高度很小,因此在這一背景下,B樹比任何二叉結構查找樹的效率都要高很多。
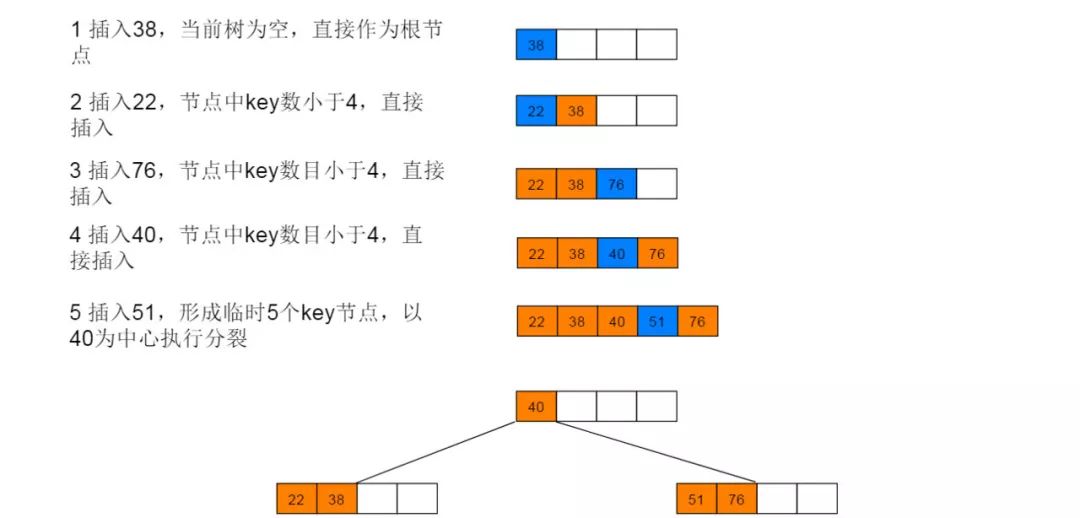
插入性能
B樹的插入會發生結點的分裂操作。當插入操作引起了 s 個節點的分裂時,磁盤訪問的次數為 h (讀取搜索路徑上的節點) +2s (回寫兩個分裂出的新節點) +1(回寫新的根節點或插入后沒有導致分裂的節點)。因此,所需要的磁盤訪問次數是 h+2s+1,最多可達到 3h+1。因此插入的代價較大。
刪除性能
B樹的刪除會發生結點合并操作。最壞情況下磁盤訪問次數是 3h=(找到包含被刪除元素需要h次讀訪問)+(獲取第2至h層的最相鄰兄弟需要h-1次讀訪問)+(在第3至h層的合并需要h-2次寫訪問)+(對修改過的根節點和第2層的兩個節點進行3次寫訪問)。
應用場景
B樹/B+樹主要用于磁盤文件組織 數據索引和數據庫索引等場景。
種樹
B+ 樹
定義
B+樹是B-樹的一種變體,B+樹相比B-樹的特點:
(1)索引節點的key值均會出現在葉子節點中。(2)索引節點中的key值在葉子節點中或者為最大值或者為最小值。(3)葉子節點使用單鏈表的形式鏈接起來。
查找性能
(1)在相同數量的待查數據下,B+樹查找過程中需要調用的磁盤IO操作要少于普通B-樹。由于B+樹所在的磁盤存儲背景下,因此B+樹的查找性能要好于B-樹。
(2)B+樹的查找效率更加穩定,因為所有葉子結點都處于同一層中,而且查找所有關鍵字都必須走完從根結點到葉子結點的全部歷程。因此同一顆B+樹中,任何關鍵字的查找比較次數都是一樣的。而B樹的查找是不穩定的。
插入性能
B+樹的插入過程與B樹類似,性能也基本一致。
刪除性能
刪除性能與B樹也基本一致。
應用場景
B樹/B+樹主要用于磁盤文件組織 數據索引和數據庫索引等場景。
種樹

霍夫曼樹
定義
給定 n 個權值作為 n 個葉子結點,構造一棵二叉樹,若該樹的帶權路徑長度達到最小,稱這樣的二叉樹為最優二叉樹,也稱為霍夫曼樹(Huffman Tree)。
霍夫曼樹是帶權路徑長度最短的樹,權值較大的結點離根較近。
應用場景
霍夫曼樹主要用于霍夫曼編碼,進行數據壓縮領域。
霍夫曼編碼
-
磁盤
+關注
關注
1文章
379瀏覽量
25209 -
C++
+關注
關注
22文章
2108瀏覽量
73651 -
二叉樹
+關注
關注
0文章
74瀏覽量
12325
原文標題:植樹節,程序員要爬哪些“樹”?
文章出處:【微信號:rgznai100,微信公眾號:rgznai100】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
不會單片機,今天被一程序猿羞辱了....
總結一下429時鐘樹的一些知識
普及一下MSP430的中斷系統
帶你了解一下人工智能中的決策樹(DT)
行走在崩潰邊緣,程序猿“自救”指南!
一種基于程序向量樹的代碼克隆檢測方法

小猿推薦MCUXpresso 軟件和工具





 普及一下程序猿們經常遇見的樹
普及一下程序猿們經常遇見的樹











評論