摘要
本文介紹了我們使用模擬設備的慣性測量單元(IMU)傳感器ADIS16470和PNI的地磁傳感器RM3100構建的捷聯慣性導航系統(SINS)。實現了基于磁力,角速率和重力(MARG)的SINS的一些基本過程,包括電磁羅盤校準,使用擴展卡爾曼濾波器(EKF)的姿態和航向參考系統(AHRS)以及跟蹤跟蹤。還實現了使用最小平方誤差(MSE)方法松散耦合傳感器融合。顯示了每個過程步驟中的算法和實驗設置。本文最后討論了結果分析和提高精度的方法。
簡介
隨著服務機器人市場和技術的發展,導航成為一項熱門研究和應用點。與車輛,船舶或飛機相比,服務機器人體積小,成本低,因此它們的導航系統應該是捷聯和低成本的。傳統的穩定平臺導航系統通常涉及單獨的加速器和光纖或基于激光的陀螺儀,所有部件都機械且剛性地安裝在與移動車輛隔離的穩定平臺上。這導致尺寸大,可靠性差和成本高的缺點。相反,在捷聯導航系統中,慣性傳感器直接固定在車輛的車身上,這意味著傳感器與車輛一起旋轉。這種捆綁方法消除了穩定平臺導航的缺點。但是,平臺導航的準確性通常高于SINS。平臺導航通常可以達到戰略等級(0.0001°/小時陀螺儀偏差,1μ g 加速器偏壓)或軍用級(0.005°/ hr陀螺儀偏差,30μ g 加速器偏差),而大多數SINS只能達到導航等級(0.01°/ hr陀螺儀偏差,50μ g 加速器偏壓)或戰術等級(10°/ hr陀螺儀偏差,1 m g < / em>加速器偏差)。對于大多數服務機器人或AGV導航應用來說,這已足夠。
有多種導航方法,包括機器視覺,GPS,UWB,帶SLAM的激光雷達等。慣性導航始終是導航的重要組成部分,使用IMU的地方。然而,由于這種傳感器的限制 - 例如偏置誤差,橫軸誤差,噪聲,特別是偏置不穩定性 - 慣性導航通常需要伙伴傳感器定期給它一個參考或校準,這稱為傳感器融合這里。有許多傳感器可以與IMU融合,例如攝像機和里程表,但在這些傳感器中,地磁傳感器是與IMU一起獲得態度的低成本方式。
在本文中,我們使用ADI的IMU,ADIS16470和地磁傳感器,用于開發平臺和算法,以實現捷聯慣性導航系統。但是,傳感器只能提供姿態信息。對于航位推算或距離測量,我們只能使用IMU中的加速度傳感器。
ADIS16470 IMU簡介
ADI公司的ADIS16470是一款集成了3軸陀螺儀的微型MEMS IMU和一個3軸加速度計。它為陀螺儀提供8°/ hr的偏置穩定性,為加速度計提供13μ g 偏置穩定性,同時其關鍵參數經過工廠校準。此外,ADIS16470的低成本價格在同級產品中具有吸引力,并被許多客戶廣泛使用。在本文中,我們使用微控制器與ADIS16470通過SPI接口進行通信。
地磁傳感器介紹
地磁傳感器是一種用于測量羅盤體內地磁場的傳感器坐標(即框架),它為標題提供絕對參考。其x,y和z分量值從本地地磁場投射。這種傳感器有兩個主要缺點 - 一個是它的精度和分辨率不高 - 例如,霍尼韋爾常用的羅盤傳感器HMC5883L只有12位分辨率。另一個缺點是傳感器容易受到周圍環境的干擾,因為地磁場非常弱,從毫高斯到8高斯。
盡管有這些缺點,它仍然可以在許多情況下使用,例如開放場,低EMI環境等。通過將地磁傳感器松散地耦合到IMU,我們可以在大多數環境中使用它。
< p>在本文中,我們使用高性能羅盤傳感器,PNI傳感器公司的RM3100,提供24位分辨率。 PNI使用主動激勵方法來提高抗噪聲能力。
羅盤傳感器的校準
在使用羅盤傳感器之前,需要對其進行校準以消除兩個主要誤差。一個是偏移誤差,這最初是由傳感器和電路的偏移誤差引起的。另一個是比例誤差。這兩種誤差都容易受到周圍磁環境的干擾。例如,如果向傳感器施加x軸方向外部磁場,則會發出外部x軸偏移誤差。同時,x軸刻度也將與y軸和z軸不同。
通常用于校準磁傳感器的方法是將傳感器旋轉為xy平面中的圓,然后提取數據。一個地方的地磁場強度是一個常數值,因此繪制的數據應該是一個圓;然而,事實上,我們將看到一個橢圓形,這意味著我們需要將橢圓移動并重新縮放到以零為中心的圓。
上面提到的2D校準方法有一些缺點,需要一個加速器衡量它的傾向。我們使用3D球面擬合方法來校準羅盤傳感器。首先,我們需要將傳感器旋轉到x-y-z空間中的每個方向,并在3D坐標中繪制其值。然后我們需要使用最小平方誤差(MSE)方法將數據擬合為橢圓體。
橢球方程可以表示為
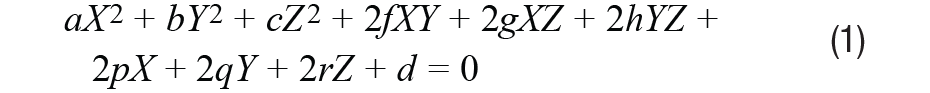
其中X,Y和Z是羅盤輸出三個方向的地磁分量。將這些值擬合為橢圓體意味著我們需要獲得系數的最佳值集。我們將系數定義為:
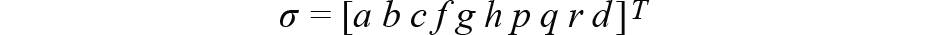
在擬合時,我們將向量定義為:
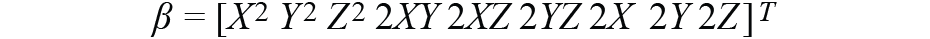
所以我們需要計算最佳σ,并使用公式2來找到最小值:

這樣我們就可以得到如圖1所示的擬合結果。
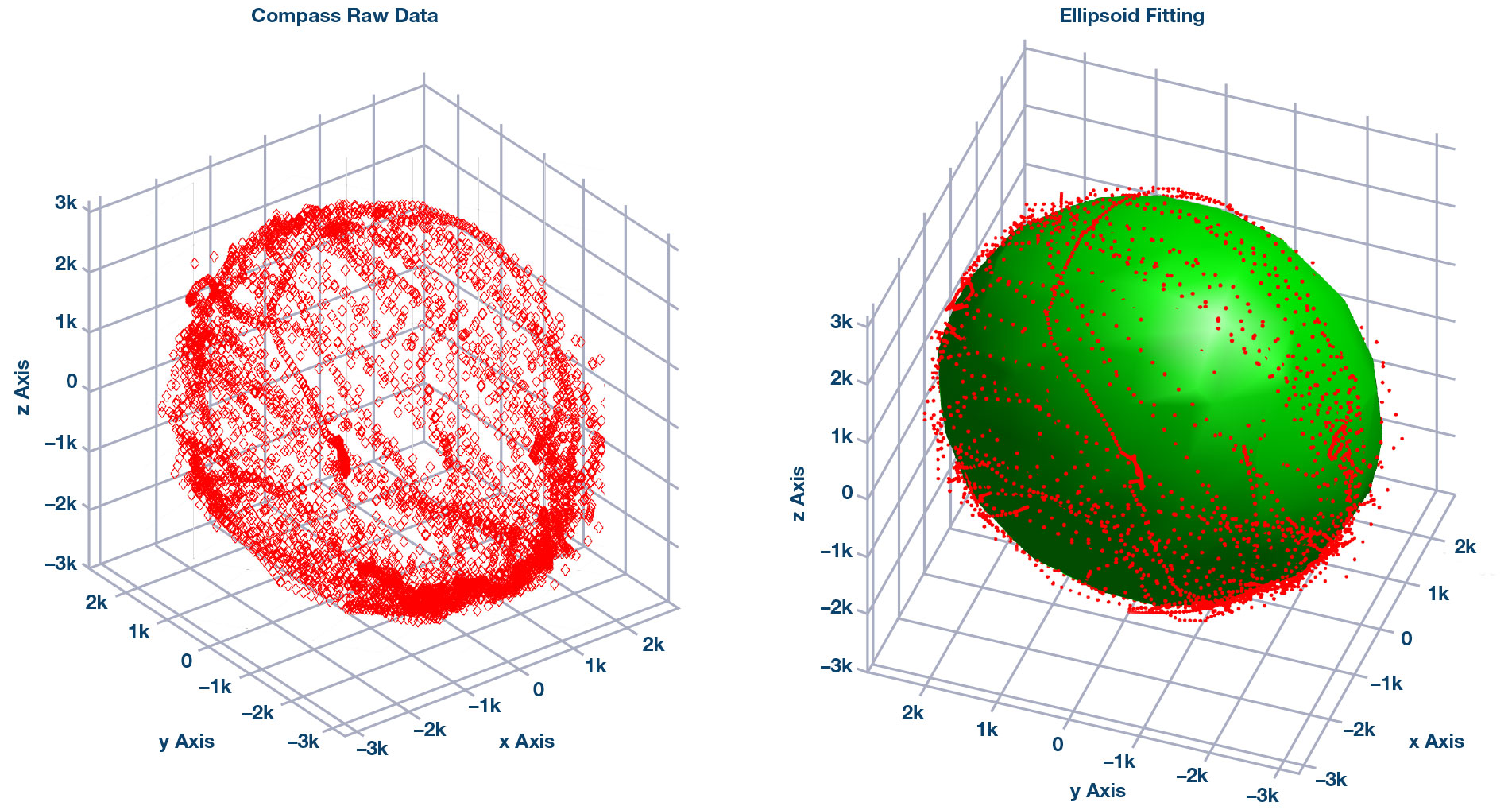
要校準傳感器,我們需要拉伸和將擬合的橢球移動到以零為中心的球體。我們使用矩陣奇異值分解(SVD)方法進行校準。后校準球如圖2所示。 1,2
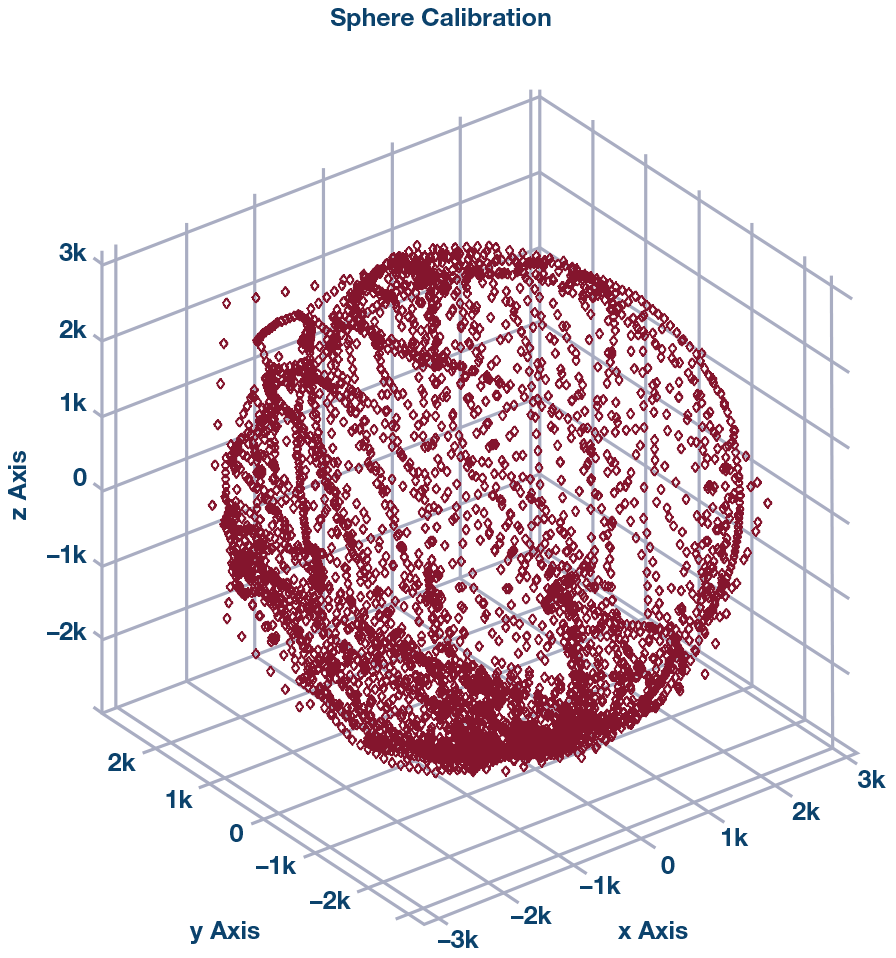
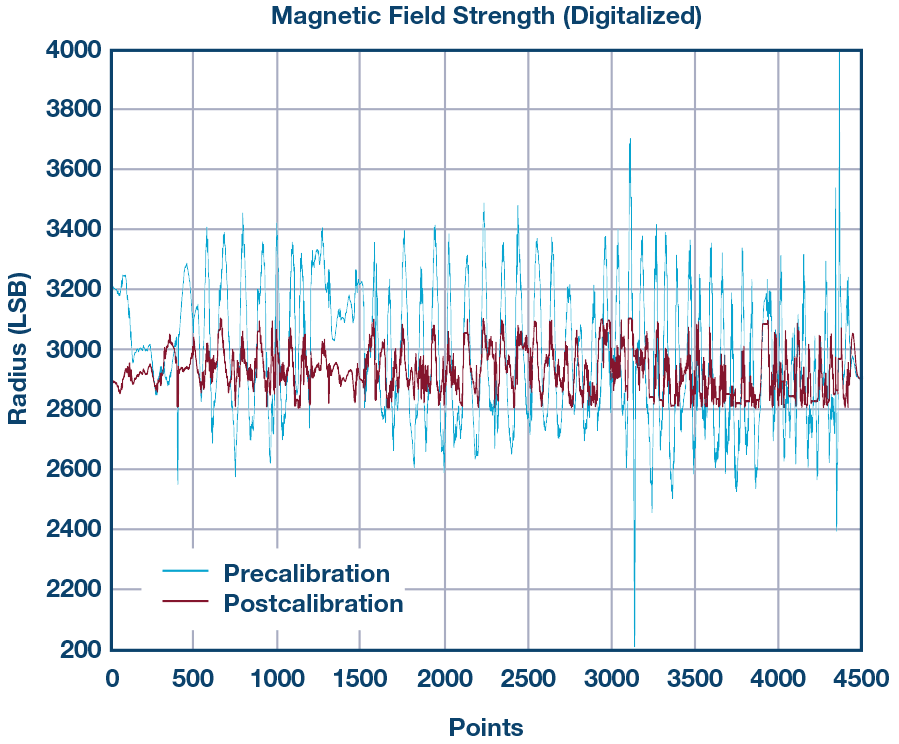
校準后,我們可以看出測得的磁場強度(球半徑)將保持幾乎恒定的值,如圖3所示。
使用ADIS16470和指南針的姿態和航向參考系統
AHRS由三個軸上的傳感器組成,提供姿態信息,包括滾轉,俯仰和偏航。 AHRS是飛機導航的概念。我們用它來描述方向;也就是說,態度。
在介紹我們的方法之前,有必要首先解釋融合的原因。實際上,我們現在的系統中有三種傳感器:陀螺儀,加速器和羅盤。
陀螺儀給出了圍繞每個軸的旋轉角速度。通過積分角速率,我們可以找到旋轉角度。如果我們知道最初的標題,我們將始終獲得標題態度。由于積分,陀螺儀的不穩定偏差將被累積,這將導致角度誤差。此外,來自陀螺儀的高斯分布噪聲將被整合到布朗運動過程中并導致隨機行走誤差。因此,我們很難長時間使用陀螺儀,并且陀螺儀需要定期校準。
加速器提供每個軸方向的加速度。在靜態狀態下,我們可以得到每個軸與重力加速度之間的角度。由于重力加速度在方向和值上是恒定的,我們可以獲得相對于重力方向的航向姿態。然而,這種方法使用重力加速度作為參考,因此無法解決圍繞重力加速度旋轉的角度。
羅盤提供從地磁場投射的每個軸的值。我們可以從每個軸與地磁場方向之間的關系推導出角度值,地磁場方向也是一個常數向量。如前一節所述,由于對外部磁場的抗擾性較差,羅盤需要一個低干擾環境。
從這個解釋中,我們可以看到很難依靠只有一個傳感器來尋找態度,我們需要結合使用兩個或三個傳感器并融合信息。本文涉及加速器,陀螺儀和地磁羅盤以找到態度。這種融合稱為磁,角速率和重力(MARG)系統。
擴展卡爾曼濾波器設計和傳感器融合
將IMU和羅盤數據融合在一起有多種方法,例如互補濾波器,統計ARMA濾波器,卡爾曼濾波器等。我們在本文中使用擴展卡爾曼濾波器。
首先,我們需要介紹本文中使用的一些定義。
坐標定義
標題或方向是兩個坐標之間的關系(是,框架)。一個坐標總是在變化,另一個坐標保持不變。對于坐標定義方法,我們使用導航坐標和身體坐標。與東北向下(NED)或地理方法相反,我們將測量的初始身體坐標值定義為導航坐標,之后是恒定坐標。從主體坐標到導航坐標的映射(投影)矩陣定義為
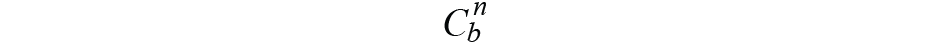
姿態定義
與歐拉角或方向余弦矩陣(DCM)矩陣不同,我們在這里使用四元數,定義為
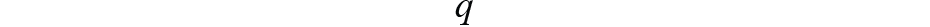
,它通常用于導航以避免參數。 3
使用卡爾曼濾波器更新姿態< / h3>
運動學方程,即狀態轉移方程,我們在本文中使用的是偏差格式,它不是線性的,因此我們需要使用EKF和偏差方程的一階線性逼近。對于EKF設計,我們定義
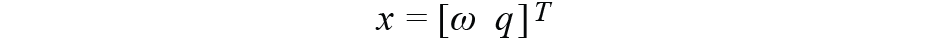
1×7向量作為狀態變量,其中
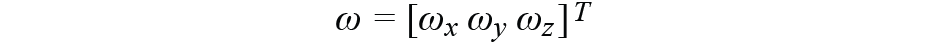
是角速率,
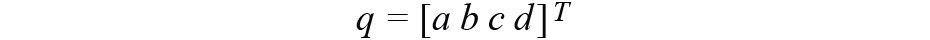
是態度四元數。
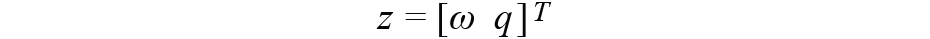
一個1×7向量,是觀察變量,它與狀態變量具有相同的成分。
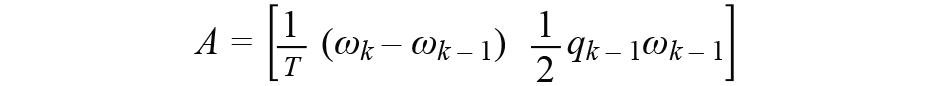
一個7×7矩陣,是狀態轉移矩陣,其中 A 中的第一部分是角速率的數字化微分方程,第二部分是數字化四元數更新方程,它是從運動學方程導出的。
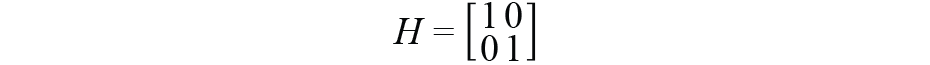
7×7矩陣,是觀察矩陣。
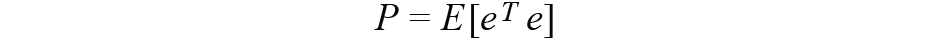
是誤差協方差矩陣,一個7×7矩陣,其中
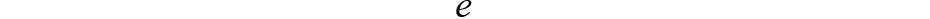
是估計的誤差向量, x ,來自真實, X 。我們在測試中將初始誤差設置為相對較小的值。它將自動收斂到一個小值。
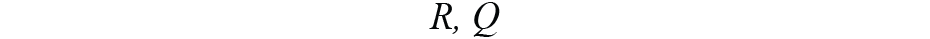
被設置為狀態轉換噪聲和觀察噪聲的噪聲協方差。我們通過測量陀螺儀和加速器的交流有效值的平方來得到它們的初始值,
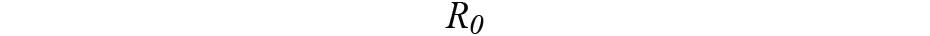
和
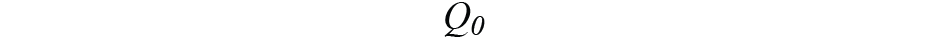
。在保持IMU和羅盤處于靜止狀態的同時,我們設置
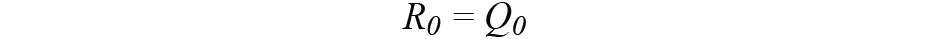
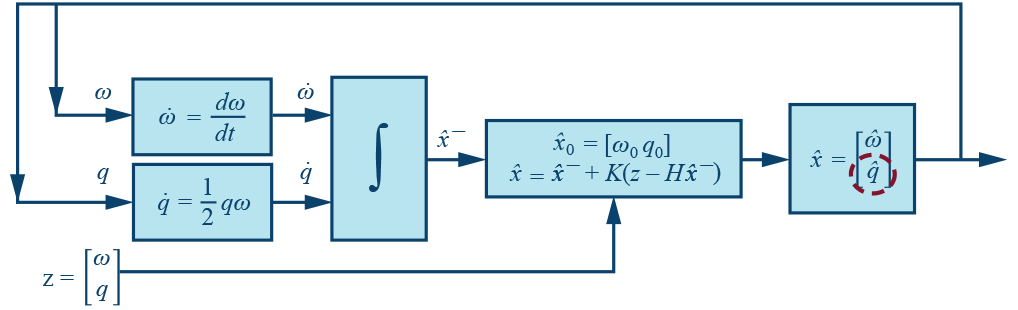
根據這個定義,我們的卡爾曼濾波器將通過以下五個步驟完成:
步驟1:使用公式3計算卡爾曼增益 K :
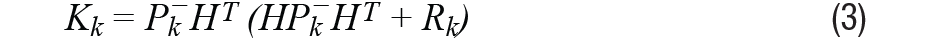
步驟2:計算誤差協方差矩陣, P :

步驟3:輸出估計狀態, x :

步驟4:預測狀態,< em> x - :

步驟5:投影誤差協方差矩陣 P - :

該過程可以簡單地描述為圖4中的框圖。
基于MSE的傳感器融合
在上一節中,觀察變量是
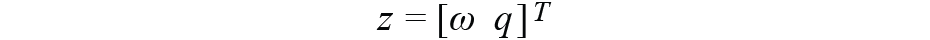
,其中沒有來自指南針的信息。由于ω是角速率,我們只能使用四元數來導入羅盤數據 q 。我們使用MSE方法得到 q ,即觀察變量中的組件。
我們將變量定義如下:
m b 和 a b :車身框架中的羅盤磁性值和加速度值。
m n 和 a n :導航框中的羅盤磁性值和加速度值。
m n0 和 a n0 :導航框架中的初始靜態羅盤磁性值和加速度值。
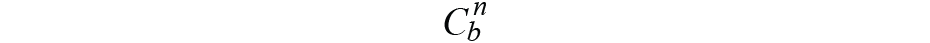
是從身體框架到導航框架的姿態轉換矩陣,用四元數表示,可以寫成
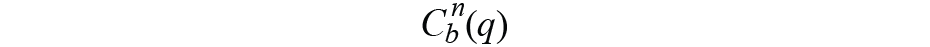
,它給出了錯誤ε,導航框架中的初始值和實時從主體框架映射到導航框架的值。
根據之前的定義,MSE方法可用于獲得最佳
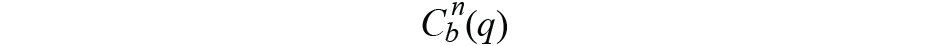
通過最小化公式8:
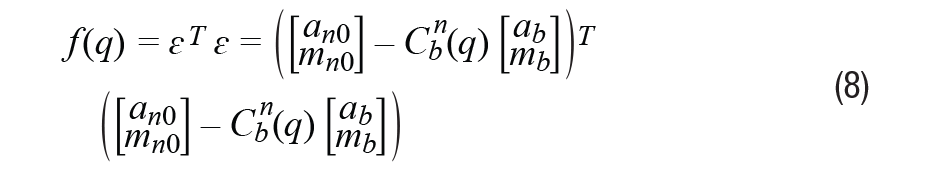
通過推導 f(q)并使其等于零,
< img src>
我們將獲得方差意義上的最佳 q 。我們使用Gauss-Newton方法用一階梯度收斂來求解上面的非線性方程。
通過組合角速率,我們將得到觀測變量

,它將羅盤數據和IMU數據融合在卡爾曼濾波器中。
過程可以是簡單地用圖5中的方框圖描述。
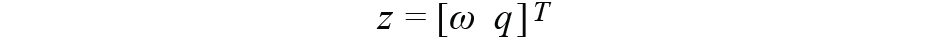
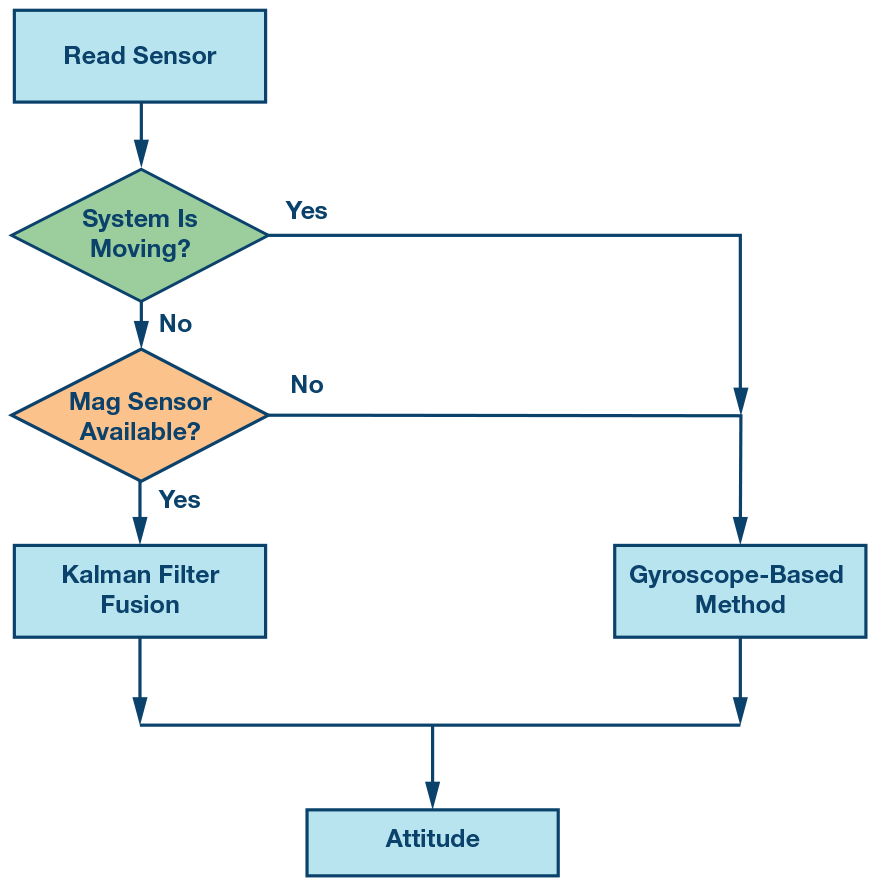
松散耦合
如前所述,我們經常遇到無法使用羅盤傳感器的情況。如果磁數據受到干擾,則解決的姿態精度將比僅使用IMU時更差。因此,我們使用松耦合,判斷磁性傳感器是否可用。當磁力傳感器不可用時,我們將僅使用IMU來找到姿態,當磁力傳感器可用時,我們將使用融合算法找到姿態,如圖6所示。

在獲得新數據或新的姿態求解周期后(在某些系統中,采樣周期與姿態解析周期不同,但我們在此處進行單個采樣周期解析),我們計算加速度的大小。如果它不等于1 g ,我們將不會使用加速器的輸出進行姿態計算。然后我們計算羅盤輸出的大小并將其與初始值進行比較。如果它們彼此不相等,我們將不會在此周期中使用地磁傳感器的數據。當兩個條件都滿足時,我們將使用卡爾曼濾波器并執行MSE融合。
航位推算(DR)使用ADIS16470
在導航中,航位推算是計算當前電流的過程通過使用先前確定的位置來定位,并基于解析周期內的已知或估計的速度或加速度推進該位置。這里將使用ADIS16470加速器。基于上一節中解決的態度,我們得到捷聯系統的移動方向,然后我們需要計算方向上的距離,最終確定位置。
航位推算方法簡介
捷聯航位推算需要使用特定的力方程來跟蹤INS的位置,該方程基于加速度測量。比力方程可以簡單地描述為方程10,方程11和方程12:

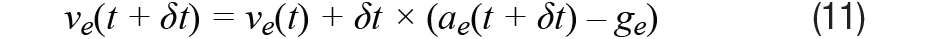
其中 a e 是地球框架中的加速度, a b 是車身框架中的加速度, v e 是地球框架中的速度, s e 是地球框架中的距離, g e 是地球框架中的重力加速度,以 g 為單位為[0 0 1]。我們需要強調的是,地球框架與導航框架不同 - 地球框架是面向NED的。這個δ t 是解析周期。
第一個等式找到從IMU體框到地球框的加速度投影,如格式所示。
第二個方程將加速度積分或累加到速度中;然而,由于測量的加速度涉及重力分量,因此需要減去重力。
與等式11類似,等式12將速度積分到距離中。
傳統方法存在一些問題。
加速器輸出總是有偏差,與重力相結合,使其難以在公式10中減去,因此更準確的表達應該是:
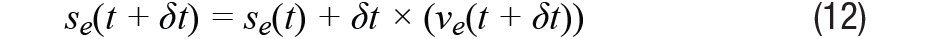 除非使用一些專業設備,例如作為分割頭。
除非使用一些專業設備,例如作為分割頭。
數值積分方法,傳統方法,通常使用零階持有者方法(前一個值)進行積分。但是,對于連續移動,這將引入重大錯誤。例如,讓我們比較以下方法:
方法1:
(Zeroth-order holder)
方法2:
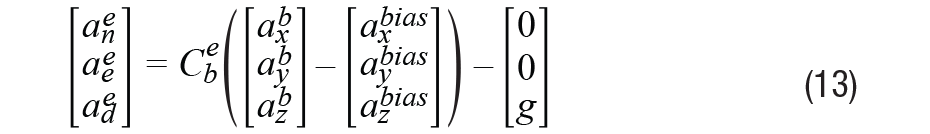
(線性插值)
在5秒內加速度為0.5 m / s 2 時,位移將相差4 m 。仿真結果如圖7所示。
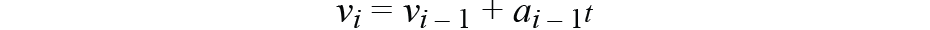
基于前面的討論,我們修改了傳統特定力方程的兩個點用于我們的應用:
我們不要將地球坐標用作導航框架。相反,正如我們在尋找先前態度時所做的那樣,我們使用初始態度
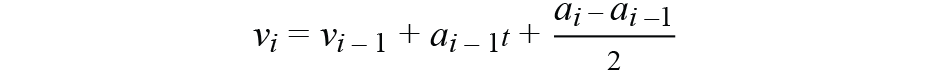
作為導航框架。通過這種方式,偏差和重力都可以輕松取消,如公式14所示:
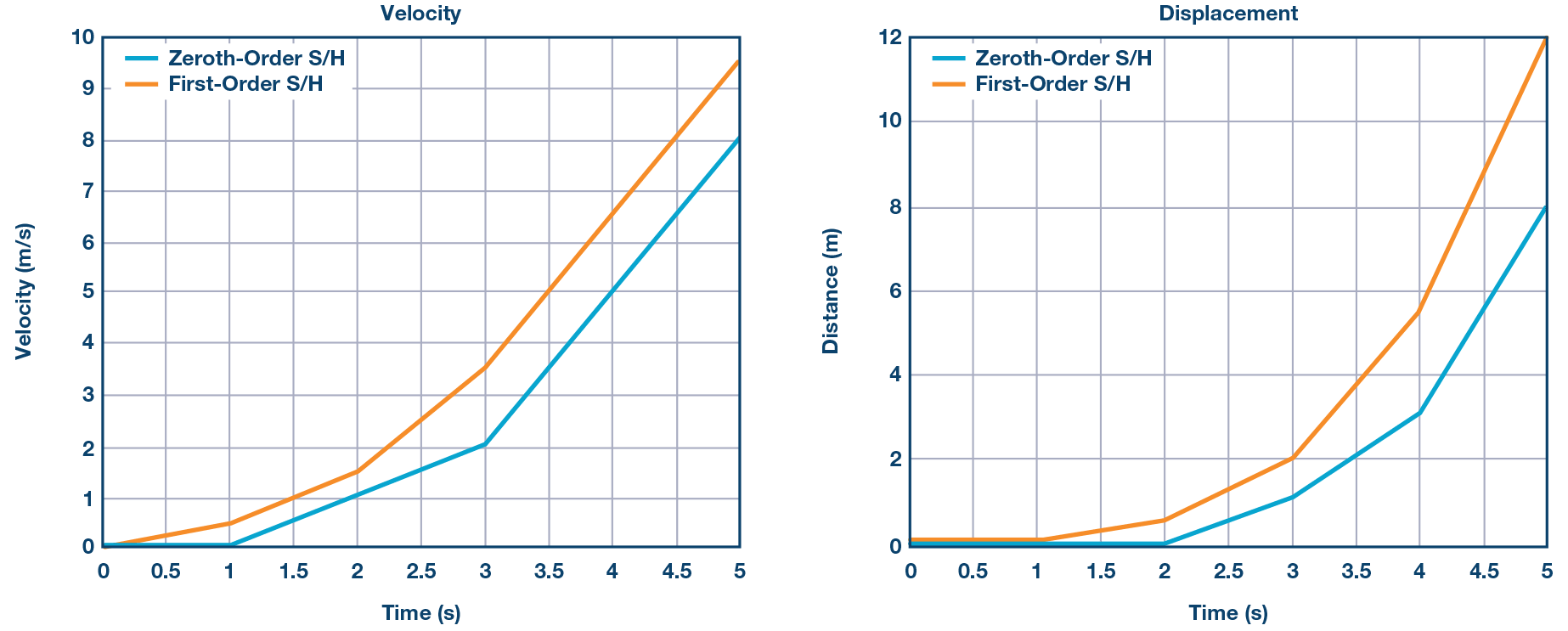
雖然偏差和重力分量包含在初始姿態中,但我們這樣做不需要將它們分開來獲取每個組件,而是我們可以直接減去它們。
比較零階保持器和一階插值,我們使用一階來獲得更準確的積分結果。
運動學模式和零速度更新技術(ZUPT)
通過使用IMU的初始值作為導航框架,我們可以部分取消加速器的初始偏差影響。然而,即使我們在使用設備之前使用分割頭可以準確地測量偏差,仍然很難取消,除非我們使用另一個精確的傳感器來定期校準它。這主要是由兩部分引起的:一部分是偏差不穩定,這意味著我們之前測量的偏差現在不是實際偏差。另一種是速度隨機游走,它是加速度的組成部分。前面提到的不希望的特性將使我們計算的距離顯著漂移。即使我們停止移動并保持靜止,加速度積分的速度仍然存在,距離仍然會增加。
要解決這個問題,我們需要找到一種方法來使用ZUPT重置速度技術。 ZUPT技術緊密依賴于應用,因此我們需要獲得系統和應用的運動學特征,然后給出我們算法的一些規則。我們找到的運動學模式越多,我們的結果就越準確。
我們通過移動帶有SINS系統的轉椅來應用我們的實驗。由于我們的研究不僅限于特定應用,我們使用以下運動學假設:
對于航位推算,導航框架中沒有z軸移動。此限制僅適用于航位推算,不用于態度解決。顯然,我們正在2D空間中移動系統。這有助于消除z軸誤差。
停止后發生所有轉彎。如果在移動時發生轉彎,則會影響姿態分辨,因為將涉及額外的加速度。
如果系統正在移動,加速度不能保持不變超過500毫秒。速度不能保持不變超過2秒。由于我們正在推動或拉動轉椅,因此難以手動地將力精確地保持不變超過500毫秒,并且人們難以以均勻的速度持續推動轉椅超過2秒。事實上,我們正在使用此規則來執行ZUPT。
加速度不能大于±1 m / s 2 。這個規則用于一些噪音過濾,這是基于我們在椅子上的拉力或推力,它不會很大。
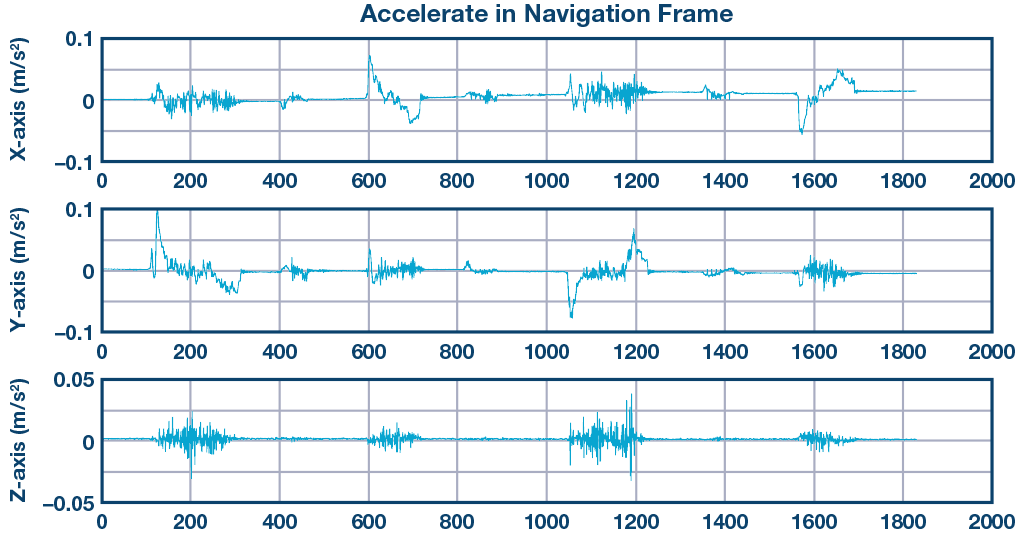
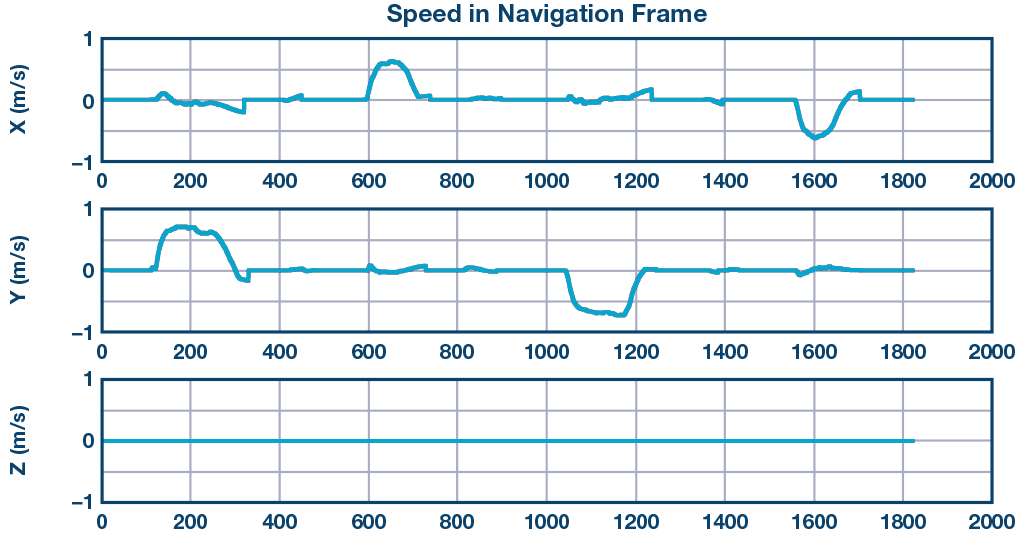
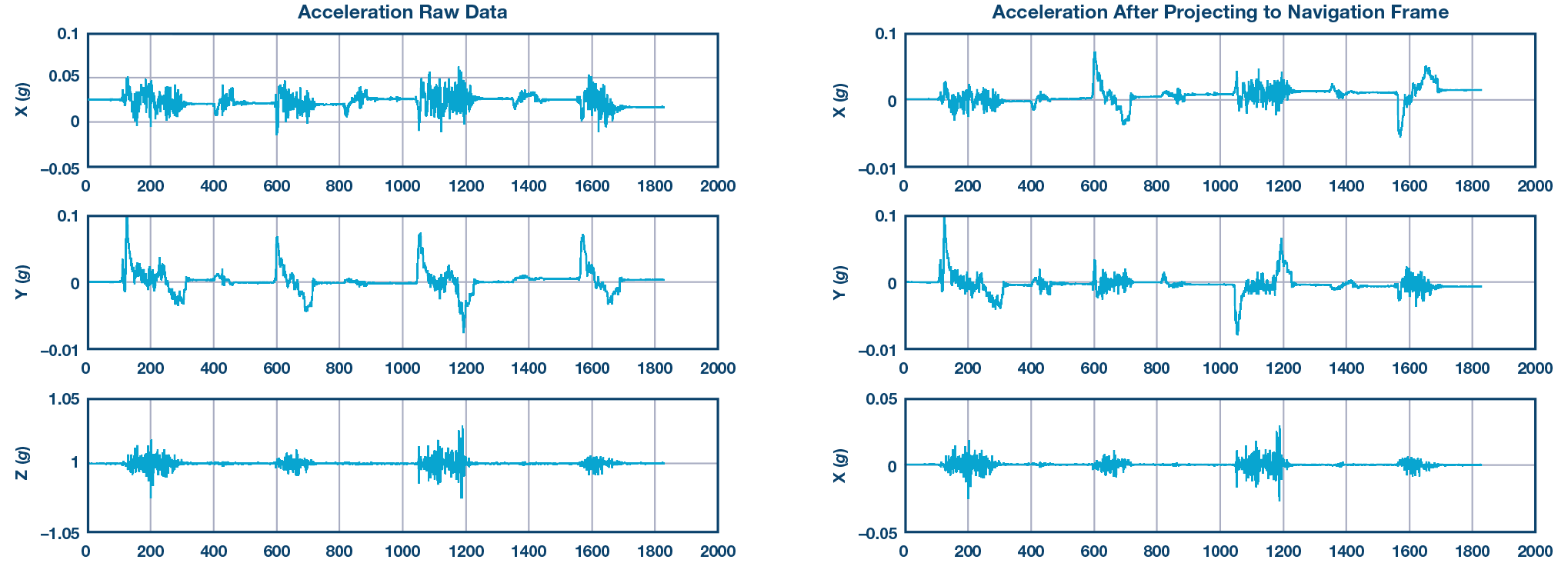
如圖8所示,當系統在X方向上移動時(投影到導航框后),Y方向也會產生加速度,在積分后,Y方向速度不會為零,這意味著即使我們只是在X方向上移動,航位推算系統仍會給我們Y分量。
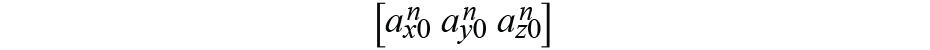
基于第三個運動學假設,我們可以使用ZUPT來取消此錯誤。 ZUPT之后的積分速度如圖9所示。
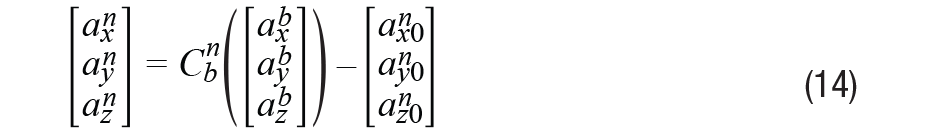
雖然我們使用了第三個假設,如前所示,但錯誤仍然無法完全取消。誤差消除取決于設定的零加速度和零速度的閾值。但是,大多數錯誤已得到糾正。
基線移位取消
雖然使用了ZUPT,但零加速有時仍可能無法到達。這導致兩個因素:
我們不能完全取消使用ZUPT的偏差不穩定性誤差和速度隨機游走。
我們解決的態度有一些誤差,將導致投影(從車身框架到導航框架)加速度誤差。
以圖10為例。圖10中的左圖是ADIS16470的原始數據(主體框架),圖10中的右圖是導航框架中投影的加速度。可以看出,當它停止移動時,預計的加速度不為零。由于它總是在變化,我們稱之為基線變化。
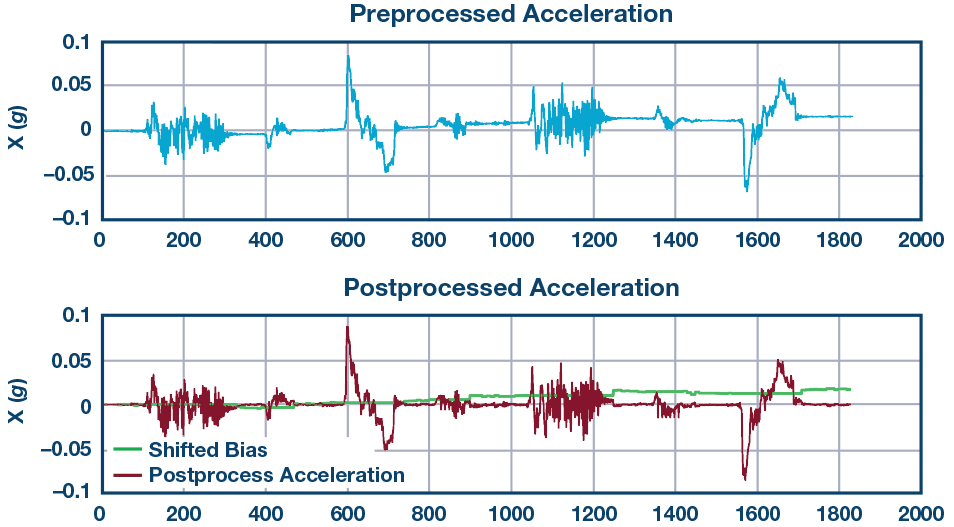
為了取消基線偏移,我們需要實時連續獲得偏移偏差并從投影加速度中減去偏差。結果如圖11所示。
上圖是基線偏移取消前的加速度,下圖中的綠色跡線是我們計算的基線偏移,紅色跡線是基線偏移消除后的加速度。
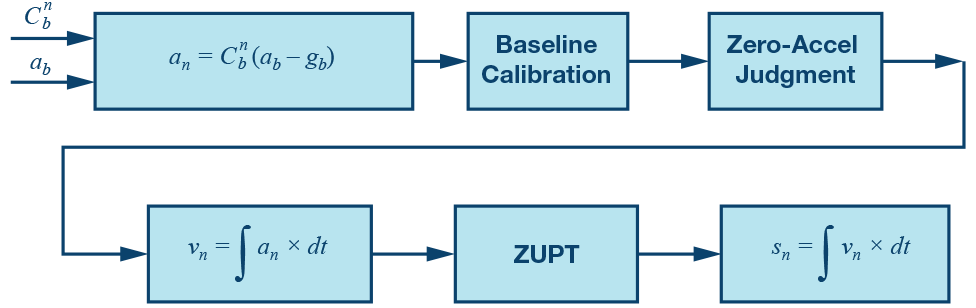
可以使用圖12中的框圖簡要描述航位推算過程。我們輸入車身框架加速度 a b 和姿態轉換矩陣(來自AHRS)
到DR系統。完成后,我們將獲得導航框架中的位置。
實驗結果和結論
實驗結果
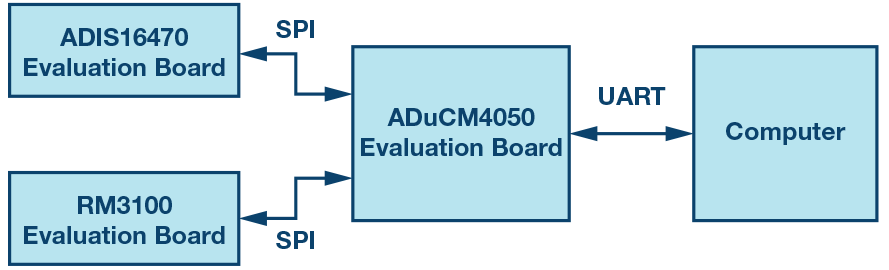
我們構建系統,如圖13所示,使用SPI端口將ADIS16470評估板和RM3100羅盤評估板連接到ADI公司的ADuCM4050電路板。 ADuCM4050調整數據格式并進行時間同步(因為IMU和指南針的數據速率不同)。然后使用UART將捕獲的數據傳輸到計算機。所有計算,包括校準,AHRS和DR,都在MATLAB ?中進行。
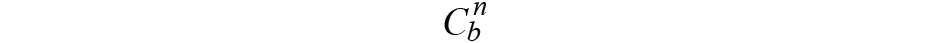
通過將電路板和計算機放在轉椅上實現實驗在我們的實驗室里把轉椅推到一個圓圈里。
AHRS輸出:態度以四元數格式和DCM格式顯示,如圖14所示。
DR輸出:航位推測結果XYZ位置和3D繪圖如圖15所示。
結論
本文介紹了使用ADI的IMU構建導航系統的基本過程ADIS16470和地磁傳感器RM3100引入了我們使用的校準,AHRS和DR方法。在平臺和實驗環境等條件有限的情況下,我們很難進一步測試平臺和算法。
有很多方法可用于改善結果,例如:
使用里程表或UWB距離測量將加速器與IMU融合,以在DR中獲得更好的距離。
使用更復雜的運動學模型,該模型涉及更多特征。 AHRS和DR中的傳感器級別和系統級別,例如系統的振動,加速度和減速度模型,地面平整度等。這意味著為計算提供更多的邊界條件,以獲得更準確的結果。
使用更精確的數值計算方法,例如使用Simpson規則或三次樣條插值在DR中進行積分,或者使用牛頓法代替Gauss-Newton方法來求解非線性MSE方程等。
最后,但最重要的是,我們f在實驗中,INS與應用或運動學模式密切相關。例如,我們在兩個地方進行了實驗:一個沒有鋪地毯的實驗室和一個鋪有地毯的辦公室。如果我們使用相同的參數集,DR結果會顯示出巨大的差異。因此,無論哪種應用,例如患者跟蹤,AGV導航或停車定位,或同一應用中的不同條件,我們都需要全面了解其運動學模型。
-
傳感器
+關注
關注
2551文章
51104瀏覽量
753610 -
IMU
+關注
關注
6文章
312瀏覽量
45753
發布評論請先 登錄
相關推薦
從IMU與地磁傳感看融合導航
【STM32G431試用申請】低成本捷聯慣導
捷聯慣導_航位推算組合導航算法研究
基于TMS320C5410和ADuC834微處理器實現壓電捷聯慣導系統的設計
IMU內有什么傳感器-慣導專題
使用ADIS16470和PNI地磁傳感器RM3100構建的捷聯慣性導航系統





 基于IMU和地磁傳感器的捷聯慣導系統
基于IMU和地磁傳感器的捷聯慣導系統
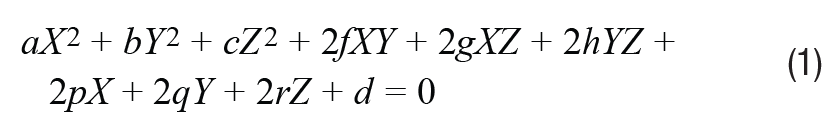










評論