可能很多人在大一的時候，就已經接觸了遞歸了，不過，我敢保證很多人初學者剛開始接觸遞歸的時候，是一臉懵逼的，我當初也是，給我的感覺就是，遞歸太神奇了！

可能也有一大部分人知道遞歸，也能看的懂遞歸，但在實際做題過程中，卻不知道怎么使用，有時候還容易被遞歸給搞暈。也有好幾個人來問我有沒有快速掌握遞歸的捷徑啊。說實話，哪來那么多捷徑啊，不過，我還是想寫一篇文章，談談我的一些經驗，或許，能夠給你帶來一些幫助。

為了兼顧初學者，我會從最簡單的題講起！

遞歸的三大要素

第一要素：明確你這個函數想要干什么

對于遞歸，我覺得很重要的一個事就是，這個函數的功能是什么，他要完成什么樣的一件事，而這個，是完全由你自己來定義的。也就是說，我們先不管函數里面的代碼什么，而是要先明白，你這個函數是要用來干什么。

例如，我定義了一個函數

1//算n的階乘(假設n不為0)2intf(intn){34}

這個函數的功能是算 n 的階乘。好了，我們已經定義了一個函數，并且定義了它的功能是什么，接下來我們看第二要素。

第二要素：尋找遞歸結束條件

所謂遞歸，就是會在函數內部代碼中，調用這個函數本身，所以，我們必須要找出遞歸的結束條件，不然的話，會一直調用自己，進入無底洞。也就是說，我們需要找出當參數為啥時，遞歸結束，之后直接把結果返回，請注意，這個時候我們必須能根據這個參數的值，能夠直接知道函數的結果是什么。

例如，上面那個例子，當 n = 1 時，那你應該能夠直接知道 f(n) 是啥吧？此時，f(1) = 1。完善我們函數內部的代碼，把第二要素加進代碼里面，如下

1//算n的階乘(假設n不為0)2intf(intn){3if(n==1){4return1;5}6}

有人可能會說，當 n = 2 時，那我們可以直接知道 f(n) 等于多少啊，那我可以把 n = 2 作為遞歸的結束條件嗎？

當然可以，只要你覺得參數是什么時，你能夠直接知道函數的結果，那么你就可以把這個參數作為結束的條件，所以下面這段代碼也是可以的。

1//算n的階乘(假設n>=2)2intf(intn){3if(n==2){4return2;5}6}

注意我代碼里面寫的注釋，假設 n >= 2，因為如果 n = 1時，會被漏掉，當 n <= 2時，f(n) = n，所以為了更加嚴謹，我們可以寫成這樣：

1//算n的階乘(假設n不為0)2intf(intn){3if(n<=?2){4????????return?n;5????}6}

第三要素：找出函數的等價關系式

第三要素就是，我們要不斷縮小參數的范圍，縮小之后，我們可以通過一些輔助的變量或者操作，使原函數的結果不變。

例如，f(n) 這個范圍比較大，我們可以讓 f(n) = n * f(n-1)。這樣，范圍就由 n 變成了 n-1 了，范圍變小了，并且為了原函數f(n) 不變，我們需要讓 f(n-1) 乘以 n。

說白了，就是要找到原函數的一個等價關系式，f(n) 的等價關系式為 n * f(n-1)，即

f(n) = n * f(n-1)。

這個等價關系式的尋找，可以說是最難的一步了，如果你不大懂也沒關系，因為你不是天才，你還需要多接觸幾道題，我會在接下來的文章中，找 10 道遞歸題，讓你慢慢熟悉起來。

找出了這個等價，繼續完善我們的代碼，我們把這個等價式寫進函數里。如下：

1//算n的階乘(假設n不為0)2intf(intn){3if(n<=?2){4????????return?n;5????}6????//?把?f(n)?的等價操作寫進去7????return?f(n-1)?*?n;8}

至此，遞歸三要素已經都寫進代碼里了，所以這個 f(n) 功能的內部代碼我們已經寫好了。

這就是遞歸最重要的三要素，每次做遞歸的時候，你就強迫自己試著去尋找這三個要素。

還是不懂？沒關系，我再按照這個模式講一些題。

有些有點小基礎的可能覺得我寫的太簡單了，沒耐心看？少俠，請繼續看，我下面還會講如何優化遞歸。當然，大佬請隨意，可以直接拉動最下面留言給我一些建議，萬分感謝！

案例1：斐波那契數列

斐波那契數列的是這樣一個數列：1、1、2、3、5、8、13、21、34….，即第一項 f(1) = 1,第二項 f(2) = 1…..,第 n 項目為 f(n) = f(n-1) + f(n-2)。求第 n 項的值是多少。

1、第一遞歸函數功能

假設 f(n) 的功能是求第 n 項的值，代碼如下：

1intf(intn){23}

2、找出遞歸結束的條件

顯然，當 n = 1 或者 n = 2 ,我們可以輕易著知道結果 f(1) = f(2) = 1。所以遞歸結束條件可以為 n <= 2。代碼如下：

1intf(intn){2if(n<=?2){3????????return?1;4????}5}

第三要素：找出函數的等價關系式

題目已經把等價關系式給我們了，所以我們很容易就能夠知道 f(n) = f(n-1) + f(n-2)。我說過，等價關系式是最難找的一個，而這個題目卻把關系式給我們了，這也太容易，好吧，我這是為了兼顧幾乎零基礎的讀者。

所以最終代碼如下：

1intf(intn){2//1.先寫遞歸結束條件3if(n<=?2){4????????return?1;5????}6????//?2.接著寫等價關系式7????return?f(n-1)?+?f(n?-?2);8}

搞定，是不是很簡單？

零基礎的可能還是不大懂，沒關系，之后慢慢按照這個模式練習！好吧，有大佬可能在吐槽太簡單了。

案例2：小青蛙跳臺階

一只青蛙一次可以跳上1級臺階，也可以跳上2級。求該青蛙跳上一個n級的臺階總共有多少種跳法。

1、第一遞歸函數功能

假設 f(n) 的功能是求青蛙跳上一個n級的臺階總共有多少種跳法，代碼如下：

1intf(intn){23}

2、找出遞歸結束的條件

我說了，求遞歸結束的條件，你直接把 n 壓縮到很小很小就行了，因為 n 越小，我們就越容易直觀著算出 f(n) 的多少，所以當 n = 1時，你知道 f(1) 為多少吧？夠直觀吧？即 f(1) = 1。代碼如下：

1intf(intn){2if(n==1){3return1;4}5}

第三要素：找出函數的等價關系式

每次跳的時候，小青蛙可以跳一個臺階，也可以跳兩個臺階，也就是說，每次跳的時候，小青蛙有兩種跳法。

第一種跳法：第一次我跳了一個臺階，那么還剩下n-1個臺階還沒跳，剩下的n-1個臺階的跳法有f(n-1)種。

第二種跳法：第一次跳了兩個臺階，那么還剩下n-2個臺階還沒，剩下的n-2個臺階的跳法有f(n-2)種。

所以，小青蛙的全部跳法就是這兩種跳法之和了，即 f(n) = f(n-1) + f(n-2)。至此，等價關系式就求出來了。于是寫出代碼：

1intf(intn){2if(n==1){3return1;4}5ruturnf(n-1)+f(n-2);6}

大家覺得上面的代碼對不對？

答是不大對，當 n = 2 時，顯然會有 f(2) = f(1) + f(0)。我們知道，f(0) = 0，按道理是遞歸結束，不用繼續往下調用的，但我們上面的代碼邏輯中，會繼續調用 f(0) = f(-1) + f(-2)。這會導致無限調用，進入死循環。

這也是我要和你們說的，關于遞歸結束條件是否夠嚴謹問題，有很多人在使用遞歸的時候，由于結束條件不夠嚴謹，導致出現死循環。也就是說，當我們在第二步找出了一個遞歸結束條件的時候，可以把結束條件寫進代碼，然后進行第三步，但是請注意，當我們第三步找出等價函數之后，還得再返回去第二步，根據第三步函數的調用關系，會不會出現一些漏掉的結束條件。就像上面，f(n-2)這個函數的調用，有可能出現 f(0) 的情況，導致死循環，所以我們把它補上。代碼如下：

1intf(intn){2//f(0)=0,f(1)=1，等價于n<=1時，f(n)?=?n。3????if(n?<=?1){4????????return?n;5????}6????ruturn?f(n-1)?+?f(n-2);7}

有人可能會說，我不知道我的結束條件有沒有漏掉怎么辦？別怕，多練幾道就知道怎么辦了。

看到這里有人可能要吐槽了，這兩道題也太容易了吧？？能不能被這么敷衍。少俠，別走啊，下面出道難一點的。

下面其實也不難了，就比上面的題目難一點點而已，特別是第三步等價的尋找。

案例3：反轉單鏈表。

反轉單鏈表。例如鏈表為：1->2->3->4。反轉后為 4->3->2->1

鏈表的節點定義如下：

1classNode{2intdate;3Nodenext;4}

雖然是 Java語言，但就算你沒學過 Java，我覺得也是影響不大，能看懂。

還是老套路，三要素一步一步來。

1、定義遞歸函數功能

假設函數 reverseList(head) 的功能是反轉但鏈表，其中 head 表示鏈表的頭節點。代碼如下：

1NodereverseList(Nodehead){23}

2. 尋找結束條件

當鏈表只有一個節點，或者如果是空表的話，你應該知道結果吧？直接啥也不用干，直接把 head 返回唄。代碼如下：

1NodereverseList(Nodehead){2if(head==null||head.next==null){3returnhead;4}5}

3. 尋找等價關系

這個的等價關系不像 n 是個數值那樣，比較容易尋找。但是我告訴你，它的等價條件中，一定是范圍不斷在縮小，對于鏈表來說，就是鏈表的節點個數不斷在變小，所以，如果你實在找不出，你就先對 reverseList(head.next) 遞歸走一遍，看看結果是咋樣的。例如鏈表節點如下

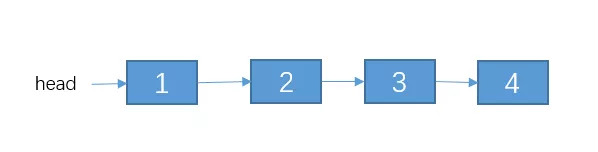
我們就縮小范圍，先對 2->3->4遞歸下試試，即代碼如下

1NodereverseList(Nodehead){2if(head==null||head.next==null){3returnhead;4}5//我們先把遞歸的結果保存起來，先不返回，因為我們還不清楚這樣遞歸是對還是錯。，6NodenewList=reverseList(head.next);7}

我們在第一步的時候，就已經定義了 reverseLis t函數的功能可以把一個單鏈表反轉，所以，我們對 2->3->4反轉之后的結果應該是這樣：

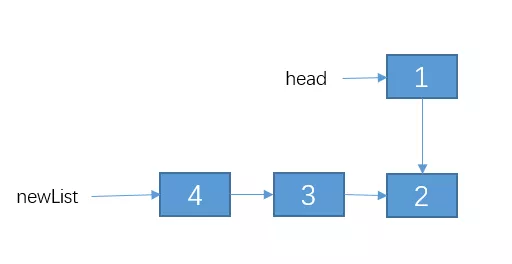
我們把 2->3->4 遞歸成 4->3->2。不過，1 這個節點我們并沒有去碰它，所以 1 的 next 節點仍然是連接這 2。

接下來呢？該怎么辦？

其實，接下來就簡單了，我們接下來只需要把節點 2 的 next 指向 1，然后把 1 的 next 指向 null,不就行了？，即通過改變 newList 鏈表之后的結果如下：

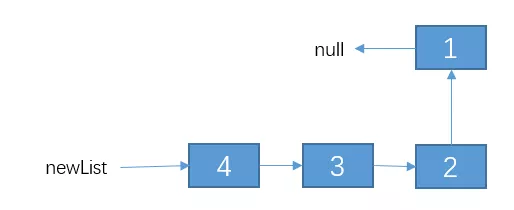
也就是說，reverseList(head) 等價于 ** reverseList(head.next)** +改變一下1，2兩個節點的指向。好了，等價關系找出來了，代碼如下(有詳細的解釋)：

1//用遞歸的方法反轉鏈表 2publicstaticNodereverseList2(Nodehead){ 3//1.遞歸結束條件 4if(head==null||head.next==null){ 5returnhead; 6} 7//遞歸反轉子鏈表 8NodenewList=reverseList2(head.next); 9//改變1，2節點的指向。10//通過head.next獲取節點211Nodet1=head.next;12//讓2的next指向213t1.next=head;14//1的next指向null.15head.next=null;16//把調整之后的鏈表返回。17returnnewList;18}

這道題的第三步看的很懵？正常，因為你做的太少了，可能沒有想到還可以這樣，多練幾道就可以了。但是，我希望通過這三道題，給了你以后用遞歸做題時的一些思路，你以后做題可以按照我這個模式去想。通過一篇文章是不可能掌握遞歸的，還得多練，我相信，只要你認真看我的這篇文章，多看幾次，一定能找到一些思路！！

我已經強調了好多次，多練幾道了，所以呢，后面我也會找大概 10 道遞歸的練習題供大家學習，不過，我找的可能會有一定的難度。不會像今天這樣，比較簡單，所以呢，初學者還得自己多去找題練練，相信我，掌握了遞歸，你的思維抽象能力會更強！

接下來我講講有關遞歸的一些優化。

有關遞歸的一些優化思路

1. 考慮是否重復計算

告訴你吧，如果你使用遞歸的時候不進行優化，是有非常非常非常多的子問題被重復計算的。

啥是子問題？ f(n-1),f(n-2)….就是 f(n) 的子問題了。

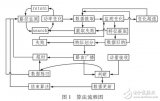
例如對于案例2那道題，f(n) = f(n-1) + f(n-2)。遞歸調用的狀態圖如下：

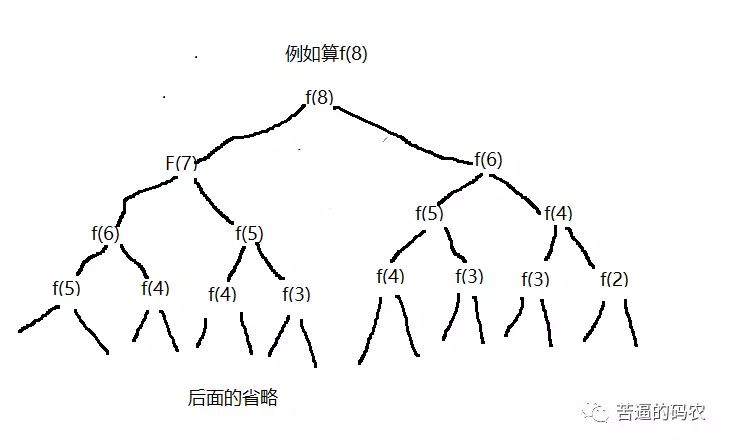
看到沒有，遞歸計算的時候，重復計算了兩次 f(5)，五次 f(4)。。。。這是非常恐怖的，n 越大，重復計算的就越多，所以我們必須進行優化。

如何優化？一般我們可以把我們計算的結果保證起來，例如把 f(4) 的計算結果保證起來，當再次要計算 f(4) 的時候，我們先判斷一下，之前是否計算過，如果計算過，直接把 f(4) 的結果取出來就可以了，沒有計算過的話，再遞歸計算。

用什么保存呢？可以用數組或者 HashMap 保存，我們用數組來保存把，把 n 作為我們的數組下標，f(n) 作為值，例如 arr[n] = f(n)。f(n) 還沒有計算過的時候，我們讓 arr[n] 等于一個特殊值，例如 arr[n] = -1。

當我們要判斷的時候，如果 arr[n] = -1，則證明 f(n) 沒有計算過，否則， f(n) 就已經計算過了，且 f(n) = arr[n]。直接把值取出來就行了。代碼如下：

1//我們實現假定arr數組已經初始化好的了。 2intf(intn){ 3if(n<=?1){ 4????????return?n; 5????} 6????//先判斷有沒計算過 7????if(arr[n]?!=?-1){ 8????????//計算過，直接返回 9????????return?arr[n];10????}else{11????????//?沒有計算過，遞歸計算,并且把結果保存到?arr數組里12????????arr[n]?=?f(n-1)?+?f(n-1);13????????reutrn?arr[n];14????}15}

也就是說，使用遞歸的時候，必要須要考慮有沒有重復計算，如果重復計算了，一定要把計算過的狀態保存起來。

2. 考慮是否可以自底向上

對于遞歸的問題，我們一般都是從上往下遞歸的，直到遞歸到最底，再一層一層著把值返回。

不過，有時候當 n 比較大的時候，例如當 n = 10000 時，那么必須要往下遞歸10000層直到 n <=1 才將結果慢慢返回，如果n太大的話，可能棧空間會不夠用。

對于這種情況，其實我們是可以考慮自底向上的做法的。例如我知道

f(1) = 1;

f(2) = 2;

那么我們就可以推出 f(3) = f(2) + f(1) = 3。從而可以推出f(4),f(5)等直到f(n)。因此，我們可以考慮使用自底向上的方法來取代遞歸，代碼如下：

1publicintf(intn){ 2if(n<=?2) 3???????????return?n; 4???????int?f1?=?1; 5???????int?f2?=?2; 6???????int?sum?=?0; 7 8???????for?(int?i?=?3;?i?<=?n;?i++)?{ 9???????????sum?=?f1?+?f2;10???????????f1?=?f2;11???????????f2?=?sum;12???????}13???????return?sum;14???}

這種方法，其實也被稱之為遞推。

最后總結

其實，遞歸不一定總是從上往下，也是有很多是從下往上的，例如 n = 1 開始，一直遞歸到 n = 1000，例如一些排序組合。對于這種從下往上的，也是有對應的優化技巧，不過，我就先不寫了，后面再慢慢寫。這篇文章寫了很久了，脖子有點受不了了，，，，頸椎病？害怕。。。。

說實話，對于遞歸這種比較抽象的思想，要把他講明白，特別是講給初學者聽，還是挺難的，這也是我這篇文章用了很長時間的原因，不過，只要能讓你們看完，有所收獲，我覺得值得！有些人可能覺得講的有點簡單，沒事，我后面會找一些不怎么簡單的題。