條件概率是機(jī)器學(xué)習(xí)模型的一種表現(xiàn)形式,應(yīng)用這一模型,對于給定的輸入X,得到各輸出類的概率,選擇最大概率的類為輸出類,如下圖:

本文介紹基于條件概率分類的兩種模型算法:邏輯斯蒂(logistic)回歸與最大熵模型,其中,logistic回歸模型和最大熵模型分別是基于最大似然函數(shù)和熵來估計模型P(y|x)。公眾號已有l(wèi)ogistic回歸模型的文章介紹,本文重點(diǎn)分析最大熵模型算法。
目錄
1. 最大熵模型算法
2. 最大熵模型例子
4. logsitic回歸模型算法
5. 總結(jié)
1.最大熵模型算法
熵是衡量隨機(jī)變量不確定性的指標(biāo),熵越大,隨機(jī)變量的不確定性亦越大。假設(shè)X是一個離散型隨機(jī)變量,其概率分布為:
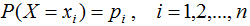
隨機(jī)變量X的熵定義為:
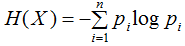
熵滿足下列不等式:

式中,|X|是x的取值個數(shù),當(dāng)且僅當(dāng)X的分布是均勻分布時,右邊的等號成立,也就是說,當(dāng)X服從均勻分布時,熵最大。
1.1 最大熵模型的定義
最大熵原理是概率模型學(xué)習(xí)的一個準(zhǔn)則,最大熵原理認(rèn)為,學(xué)習(xí)概率模型時,在所有可能的概率模型(分布)中,熵最大的模型是最好的模型。條件概率是機(jī)器學(xué)習(xí)模型的一種表現(xiàn)形式,學(xué)習(xí)該模型的一種方法是最大化該條件概率的熵,即最大化下式:

其中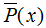 表示變量X的經(jīng)驗(yàn)分布:
表示變量X的經(jīng)驗(yàn)分布:
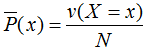
其中v(X=x)表示訓(xùn)練數(shù)據(jù)中輸入x出現(xiàn)的頻數(shù),N表示樣本容量。
(1)式的未知變量 就是需要學(xué)習(xí)的模型。
就是需要學(xué)習(xí)的模型。
我們在構(gòu)建分類模型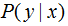 的過程中假設(shè)訓(xùn)練數(shù)據(jù)集的聯(lián)合概率分布與真實(shí)模型的聯(lián)合概率分布相等,這一假設(shè)用特征函數(shù)f(x,y)的期望來描述,特征函數(shù)的定義:
的過程中假設(shè)訓(xùn)練數(shù)據(jù)集的聯(lián)合概率分布與真實(shí)模型的聯(lián)合概率分布相等,這一假設(shè)用特征函數(shù)f(x,y)的期望來描述,特征函數(shù)的定義:

特征函數(shù)f(x,y)關(guān)于訓(xùn)練數(shù)據(jù)集的聯(lián)合概率分布的期望值,用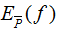 表示:
表示:
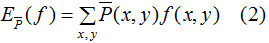
其中,
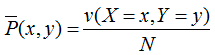
,v(X=x,Y=y)表示訓(xùn)練數(shù)據(jù)中樣本(x,y)出現(xiàn)的頻數(shù)。
特征函數(shù)f(x,y)關(guān)于模型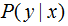 與經(jīng)驗(yàn)分布
與經(jīng)驗(yàn)分布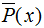 的期望值,用
的期望值,用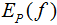 表示:
表示:

假設(shè)兩者期望相等,即:

或

結(jié)合(1)(4)式,得到最大熵模型:
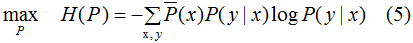
約束條件:
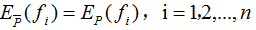
1.2 最大熵模型的學(xué)習(xí)
我們求解(5)式在約束條件下的最大值,其對應(yīng)的模型P(Y|X)就是所學(xué)習(xí)的最優(yōu)模型。
對于給定的訓(xùn)練數(shù)據(jù)集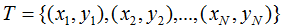 以及特征函數(shù)
以及特征函數(shù) ,i=1,2,...,n,最大熵模型的學(xué)習(xí)等價于約束最優(yōu)化問題:
,i=1,2,...,n,最大熵模型的學(xué)習(xí)等價于約束最優(yōu)化問題:

將最大值問題轉(zhuǎn)化為等價的求最小值問題:
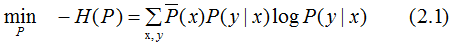
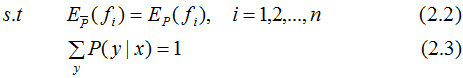
引入拉格朗日乘子 將約束的最優(yōu)化問題轉(zhuǎn)換為無約束最優(yōu)化的對偶問題,通過求解對偶問題求解原始問題。
將約束的最優(yōu)化問題轉(zhuǎn)換為無約束最優(yōu)化的對偶問題,通過求解對偶問題求解原始問題。
定義拉格朗日函數(shù)L(P,w):
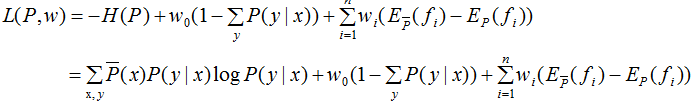
最優(yōu)化的原始問題:
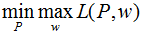
對偶問題:

令

得:
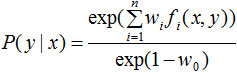
由于 ,對上式進(jìn)行歸一化得:
,對上式進(jìn)行歸一化得:
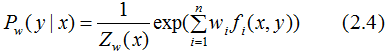
其中,
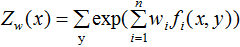
令
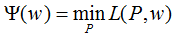
易知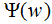 對偶問題外部的極大化問題:
對偶問題外部的極大化問題:
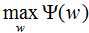
根據(jù)上式求解的 代入(2.4)式,得到最終的學(xué)習(xí)模型P(y|x)。
代入(2.4)式,得到最終的學(xué)習(xí)模型P(y|x)。
2. 最大熵模型例子
假設(shè)隨機(jī)變量Y有5個取值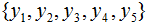 ,假設(shè)隨機(jī)變量Y的條件概率分布滿足如下條件:
,假設(shè)隨機(jī)變量Y的條件概率分布滿足如下條件:
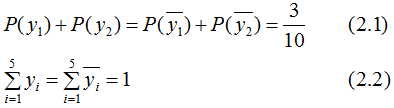
求最大熵模型對應(yīng)的概率分布P(Y)。
最大熵模型的目標(biāo)函數(shù):
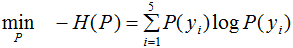
引進(jìn)拉格朗日乘子 ,定義拉格朗日函數(shù):
,定義拉格朗日函數(shù):
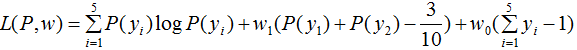
令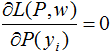 ,得:
,得:
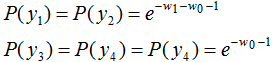
將上式代入函數(shù)L(P,w)得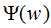 ,令
,令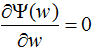 ,得:
,得:
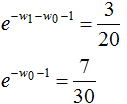
于是最大熵模型對應(yīng)的概率分布:
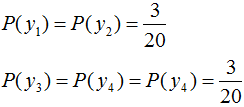
3. 熵模型在信號檢測的應(yīng)用
由第一節(jié)我們知道,熵是描述事物不確定性的指標(biāo)。我們將熵的這一性質(zhì)應(yīng)用在信號檢測領(lǐng)域,當(dāng)信號包含了較強(qiáng)的隨機(jī)噪聲時或被噪聲完全掩蓋時,信號的隨機(jī)性大大的增加了,其對應(yīng)的熵也較大,根據(jù)這一原理對信號的質(zhì)量進(jìn)行檢測,下圖是用熵檢測心電信號質(zhì)量的效果圖:

黑色表示較好的心電信號質(zhì)量,紅色表示較差的心電信號質(zhì)量。
4. logistic回歸算法
logistic回歸是一種概率分類模型,對于二分類任務(wù)來說,其條件概率分布:

我們用最小化損失函數(shù)去估計上式的模型參數(shù)。對于給定的訓(xùn)練數(shù)據(jù)集 ,其中,
,其中,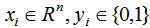 。
。
設(shè):
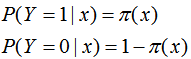
似然函數(shù)為:

對數(shù)似然函數(shù)為:
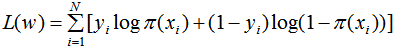
損失函數(shù)為:
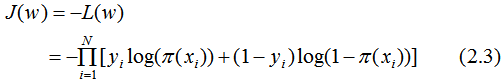
用梯度下降法求解w的估計值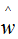 :
:

代入(2.1)(2.2)式,得到邏輯斯蒂回歸模型P(y|x),其中向量包含了b值。
5. 小結(jié)
本文介紹基于條件概率分類的兩種模型算法:logistic回歸模型與最大熵模型,其中,logistic回歸模型是基于最大似然函數(shù)估計模型P(y|x),最大熵模型是基于熵這一指標(biāo)估計模型P(y|x)。
-
模型
+關(guān)注
關(guān)注
1文章
3243瀏覽量
48836 -
機(jī)器學(xué)習(xí)
+關(guān)注
關(guān)注
66文章
8418瀏覽量
132628 -
Logistic
+關(guān)注
關(guān)注
0文章
11瀏覽量
8853
原文標(biāo)題:最大熵模型算法總結(jié)
文章出處:【微信號:AI_shequ,微信公眾號:人工智能愛好者社區(qū)】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
機(jī)器學(xué)習(xí)之偏差、方差,生成模型,判別模型,先驗(yàn)概率,后驗(yàn)概率
回歸算法有哪些,常用回歸算法(3種)詳解
Edge Impulse的回歸模型
使用KNN進(jìn)行分類和回歸
基于概率粗糙集模型的信息檢索
LTL概率模型檢驗(yàn)工具的實(shí)現(xiàn)與優(yōu)化
基于Wasserstein距離概率分布模型的非線性降維算法
基于概率主題模型的景點(diǎn)主題模型
掌握logistic regression模型,有必要先了解線性回歸模型和梯度下降法
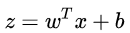
如何使用概率模型進(jìn)行非均勻數(shù)據(jù)聚類算法的設(shè)計介紹
基于交叉熵算法的跟馳模型標(biāo)定





 基于條件概率分類的兩種模型算法:logistic回歸模型與最大熵模型。
基于條件概率分類的兩種模型算法:logistic回歸模型與最大熵模型。










評論