作為數據結構的基礎，樹分很多種，像AVL樹、紅黑樹、二叉搜索樹....今天我想分享的是關于二叉樹，一種基礎的數據結構類型。

01

什么是樹

在《數據結構》[注1]中樹有如下定義：

樹是 n(n≥0) 個結點的有限集

在此我對上述定義做出如下解釋：

當n=0n=0時，為空樹，樹的深度與高度均為00，是樹的一種特例；當n>0n>0時，為非空樹，樹的第一個結點，即深度為11的結點，我們稱其為根結點，由根結點可以引出若干子樹分支，同時子樹分支可依此向下延伸，此時樹的深度與高度也在變化，即樹狀圖。

這里我們需要厘清樹的深度與樹的高度與其他樹的術語：

樹的深度：樹中結點的最大層次

樹的高度：從葉子結點開始定義，葉子結點為第一層，往上依次遞增，直至根結點。

結點：樹的結點包含一個數據元素以及若干指向其子樹的分支

度：結點所擁有的子樹數量

終端節點：度為0的結點稱為葉子結點或終端結點

樹的度：樹中各結點度的最大值

層次：從根開始定義，根為第一層，依次遞增

有序樹：樹中結點的各子樹從左往右是有次序的，不可相互交換；反之則是無序樹

森林：一棵非空樹刪掉根結點，即是森林

02

二叉樹的概念引入

二叉樹是由樹演化而來的一種數據結構，上面所有術語均適用于二叉樹。二叉樹與樹不同之處在于，樹的每一個結點（除終端結點外）允許有若干子樹分支；而二叉樹只允許有左右兩個子樹分支，即不存在度大于2結點。

C語言示例:

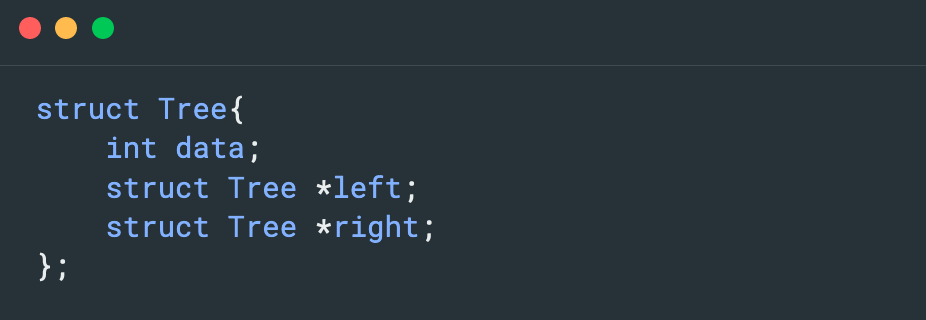
上面的示例清晰地闡明了二叉樹的結點是由一個數據元素和兩個子樹分支構成，需要明確的是，雖然終端結點沒有指向任何子樹，但它仍舊有往下繁衍的能力。

除此之外，二叉樹還是一棵有序樹，它的各個結點從左到右是依次有序可循的，且不可交換；它具有以下五種形態：

空樹

僅有根結點

左子樹為空

右子樹為空

左右子樹均非空

當二叉樹處于第五種狀態，且設樹的深度為n，總結點數為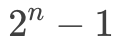?時，我們稱其為滿二叉樹。

??事實上還有另外一種也處于第五狀態的樹——完全二叉樹。由于完全二叉樹的定義在每個版本的教科書中均不相同，而筆者只接觸過《數據結構·嚴蔚敏版》，因此摘錄此書中對完全二叉樹的定義：

深度為k的，有n個結點的二叉樹，當且僅當其每一個結點都與深度為k的滿二叉樹中編號從1至n的結點一一對應時，稱之為完全二叉樹。

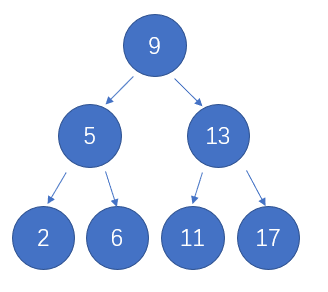
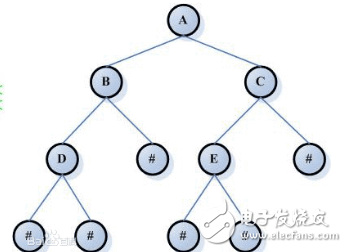
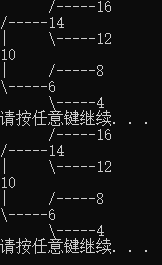
這段描述我讀了兩遍，方才理解其中的深刻含義，我們把深度為3的滿二叉樹的每個結點從上往下，從左往右進行編號：??

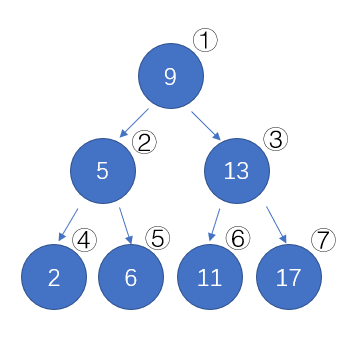
然后我們再定義一棵深度也為3的二叉樹，該二叉樹的n 個結點（n≤7），當從1到n的每個結點都與上圖中的編號結點一一對應時，這二叉樹就稱為完全二叉樹。

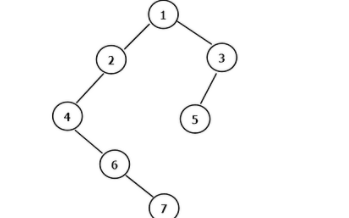
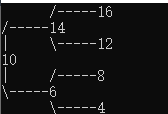
舉個例子，當n=5時：

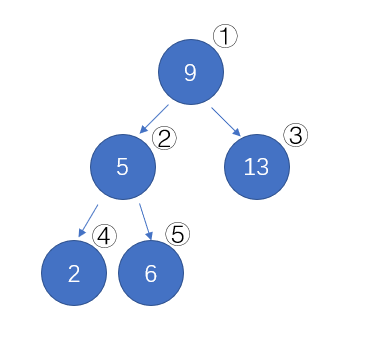
這便是完全二叉樹。

因此我們還可以得到一個推論：滿二叉樹是完全二叉樹，但完全二叉樹不一定是滿二叉樹。

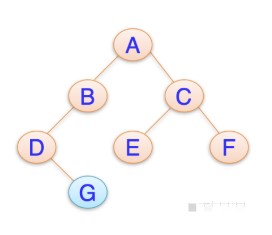
當二叉樹處于第三種狀態時，稱其為右斜樹。

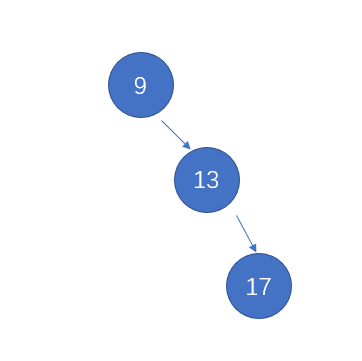
同理，處于第四狀態為左斜樹。

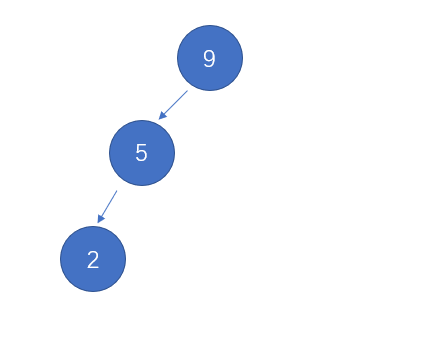
????03

二叉樹的性質總結

二叉樹的第i 層上最多有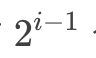個結點。此性質可通過上面滿二叉樹的圖示推得

深度為n 的二叉樹，最多擁有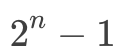?個結點。此性質可以通過數列求和得出：

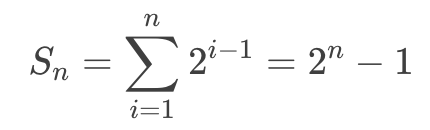
設滿二叉樹深度為 n，葉子結點數必為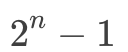

設任意一棵二叉樹的葉子結點數為n0，度為1的結點數為n1，度為2的結點數為n2；總結點數為n。則有：

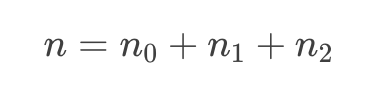
設分支的總邊數為x，則有：

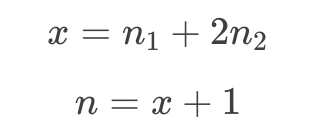
聯立上述三式可得：

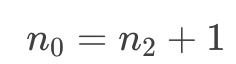
即任意二叉樹的葉子結點數為該樹中度為2的結點數的總和加一。

設一完全二叉樹具有n個結點，則其深度必為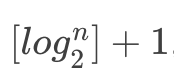，[x]?表示不大于?x?的最大整數，即向下取整。

04

手把手建立二叉樹

C語言示例：

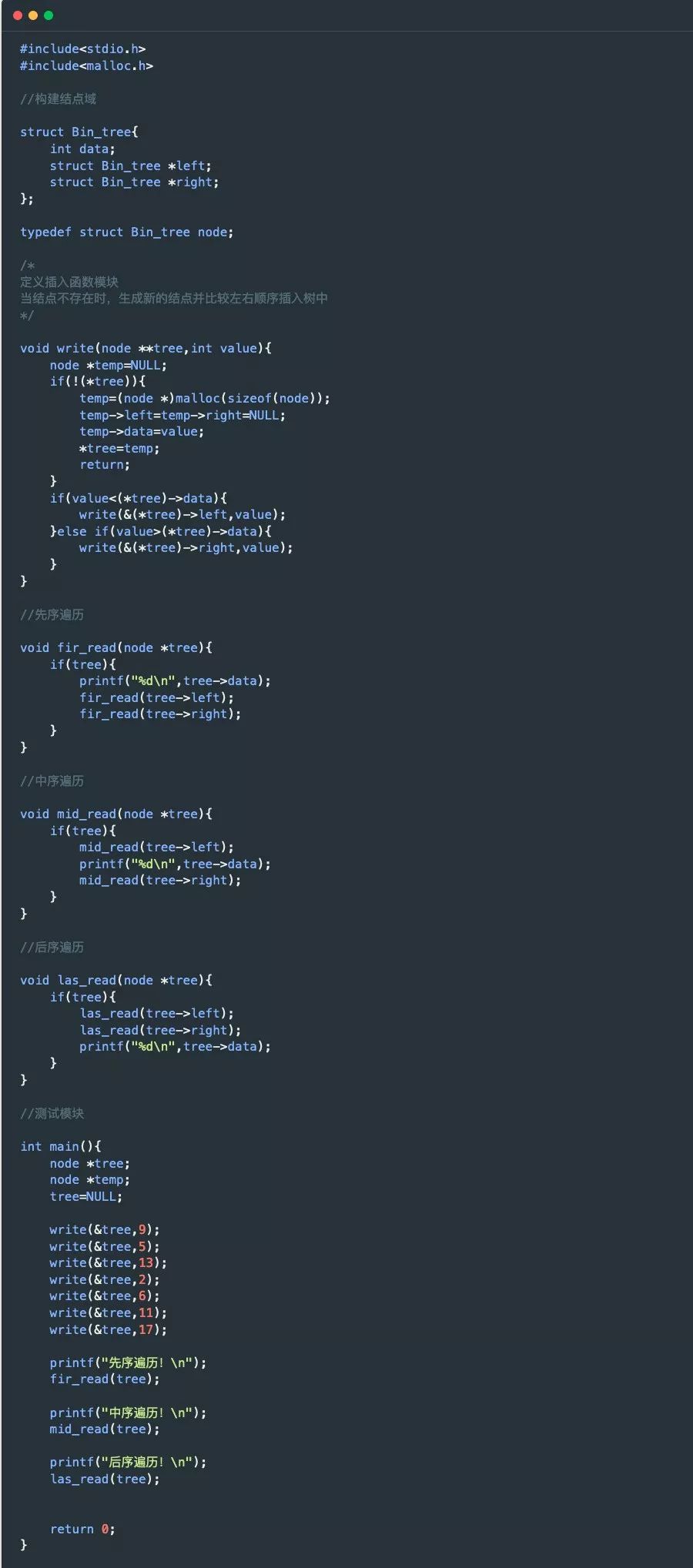
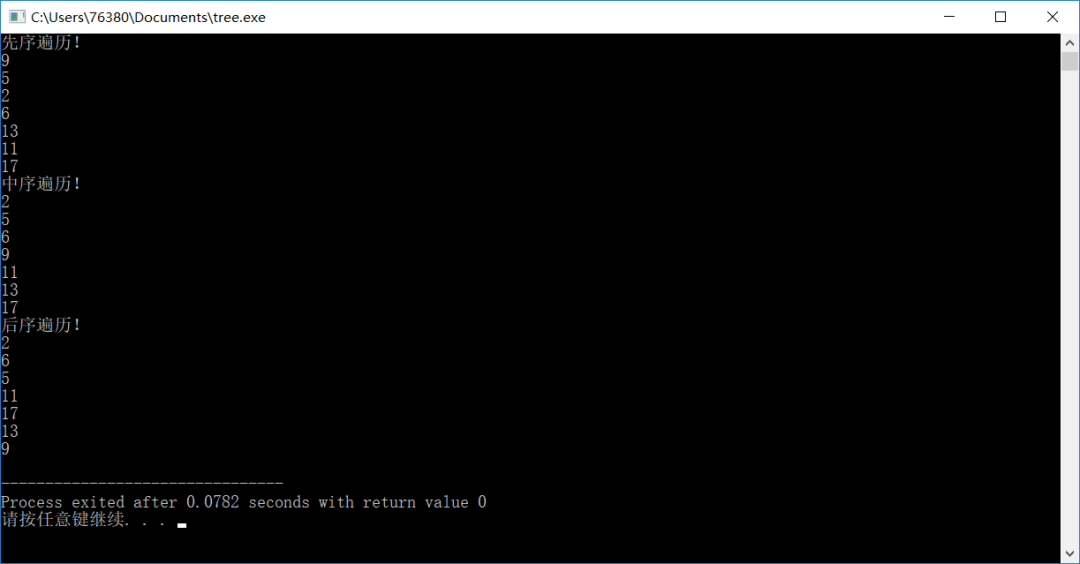
其中需要指明的是二叉樹的三種遍歷方法：先序遍歷、中序遍歷、后序遍歷。

先序遍歷

即遍歷順序為“根—>左->右”。

中序遍歷

即遍歷順序為“左—>根—>右”，由于二叉樹為有序樹，因此中序遍歷輸出的值由小到大的。

后序遍歷

即遍歷順序為“左—>右—>根”。

還有一種遍歷法，稱為層序遍歷，有興趣的讀者可以嘗試著寫一下。