之前分享過創新工場人工智能工程院執行院長王詠剛的《AI時代,提高孩子創造未來的能力,陪孩子玩什么游戲?》一文。很多家長看了文章后,想知道玩這些游戲到底有什么用?
詠剛的這篇文章在解答這個問題的同時,再介紹了幾個最近陪孩子玩過的游戲,算是上一篇文章的續篇。在此分享給大家,希望可以幫助到AI時代焦慮的父母們。
玩這些游戲有什么用?
如此發問的,大概有兩類人:一類是對孩子教育有些焦慮的家長,覺得文章內提到的游戲和孩子的日常學習關系不大,或者說,與孩子學習成績關系不大;另一類是線上線下兒童教育平臺、知識分享平臺的從業者,他們的疑問更專業些——你這些游戲教學法背后的設計思想和方法論是什么?這些游戲所訓練的思維邏輯與現實的關聯在哪里?比如,孩子玩漢諾塔游戲時建立的思維方法,未來在什么地方可以用到?
這些都是特別好的問題。但我的回答呢,也特別簡單:
我陪我們家小朋友非非玩的游戲,其實就是一個既愛玩也有好奇心的爸爸,陪一個同樣愛玩也同樣有好奇心的兒子體驗世界的過程。我想把它記錄下來,寫成文章。
這些游戲和孩子的日常學習關系不大,和孩子的學習成績也基本無關。
這些游戲背后沒有什么設計精妙、條理清晰、層次分明的教育學理念或方法論。畢竟我只是一個工程師兼業余寫作愛好者,而不是教育學家。
這些游戲與現實的最大關聯就是——我希望孩子能從小學會用正確的視角和正確的邏輯去理解這個神奇的世界,理解這個浩瀚宇宙中最有趣的事兒、最有趣的人。
正確的視角和正確的邏輯,這就是我上一篇文章所強調的“稀缺性技能體系”的核心基礎。千萬不要用功利主義或實用主義的方式去理解這種“稀缺性技能體系”,那只會讓我們逐漸遠離這些游戲的“初心”。
比如上一篇文章重點談到的漢諾塔游戲——孩子在玩游戲時,大致可以建立模糊的、初步的“分而治之”的思想,體驗一個整體任務及其嵌套或循環執行的子任務之間的關系。你知道游戲有趣、孩子喜歡就行了。如果你非要問“分治法”“迭代法”“遞歸法”到底有什么現實關聯,那不就好比學了微積分卻被老媽追問“這玩意兒能用來買菜還是能用來算賬”?
實際上,“分治”“迭代”“遞歸”都是重要的思維邏輯,你學高數會用得上,你編程序會用得上,你設計生物學實驗會用得上,你組織安排一個大型會議的運營細節會用得上,你設計一幢現代建筑會用得上,你創作一部草蛇灰線、伏延千里的小說會用得上,你為一個微信小程序做交互和視覺設計時也會用得上……可這種“用得上”或者說“現實關聯”,肯定不是“學會用電動螺絲批就能在裝配流水線上崗”那種意義上的現實關聯。
我所看重的現實關聯,更多指的是 “認知能力”“創造能力”以及“解決問題的能力”。
這個道理,懂的人自然懂。
AI時代正在到來。簡單、重復性勞動必將被機器取代。等到你我的孩子漸漸長大,你會希望他們怎么融入全新的世界?你會希望他們怎么感受人生的價值和意義?作為宇宙中最“孤獨”的智慧生物,你們,我們,你們的孩子,我們的孩子……如果大家能享受哪怕一丁點兒理解這個宇宙運行規律的快樂,或者在太陽系的尺度內創新、創造的快樂,或者在相互欣賞、喜歡的人之間分享思想與情感的快樂,這些還不夠有價值、有意義嗎?
所以,開心地陪孩子玩游戲就好;想那么多有的沒的,豈不徒增煩惱?趕快進入正題——再介紹幾個最近我陪非非玩過的游戲,算是上一篇文章的續篇。
培養理性認知:從積木游戲里看世界
人類對這個世界最直接的主觀感受,經常與現象背后的科學邏輯大相徑庭。每個人從小長大,也總會有一個不斷用理性思維去反對主觀印象的過程。
兩千多年前的人類看到大地是平的,絕大多數人會自然而然地相信“天圓地方”或“天圓地平”,但古希臘思想家和科學家卻可以通過更精妙的觀察和實驗證明地球是圓的,甚至測量地球這個球體的大小。
小朋友非非喜歡一邊玩地球儀,一邊聽我講埃拉托斯特尼測量地球周長的故事。盡管他現在還完全不懂平行線、內錯角等幾何知識,但他還是能從下面這張維基百科的示意圖中,體會到埃拉托斯特尼在設計這個測量方法時的大膽假設和縝密構思。
非非沒必要記住埃拉托斯特尼具體的實驗設計和計算方法,他只要知道,人類的主觀經驗——例如地球是平的還是圓的——必須用科學方法、科學邏輯來證實或證偽就可以了。事實上,我經常通過玩游戲的方法,來幫助非非強化“經驗不等于科學”的基本常識。
例如,我和非非玩過一個用立方體小積木來造火箭和宇宙飛船的游戲。這游戲用任何接近立方體形狀的小積木都可以玩,玩法也特別簡單,關鍵在于引導孩子做出自己的預測,然后再動手來證實或證偽。
我和非非先從最簡單的造火箭開始。我用5塊積木拼出一個概念意義上的小“火箭”,然后讓非非把火箭長度增加一倍。這極其簡單,非非不用動手就知道,要拼出一個有原火箭兩倍長的新火箭,就需要用10塊積木,因為5x2或者5+5都等于10。
建立了簡單的概念,我開始給非非“出難題”了。現在,我打算造的是一艘金字塔形狀的“宇宙飛船”——因為不考慮空氣阻力,宇宙飛船當然可以打造成任意形狀。金字塔形狀的宇宙飛船,可以參考電影《星球大戰》中的帝國級殲星艦。我先用立方體積木搭出了一個三層高的宇宙飛船,就像下圖這樣:
然后我讓非非數一下,這個三層高的宇宙飛船,一共需要幾塊積木。答案是14塊。那么,現在問題來了:我問非非,如果照這個樣子,搭建六層高的宇宙飛船,大概需要幾塊積木?如果搭建九層高的宇宙飛船呢?
非非很積極地搶答:六層高的宇宙飛船比剛才的宇宙飛船高了一倍,剛才需要14塊,那現在大概需要20多塊積木吧;九層高的宇宙飛船又增高了三層,肯定會需要30多塊吧(非非似乎是想計算14x3,但他的乘法還不過關)。
我提醒非非仔細想想,看這樣的估計有什么問題沒有。非非歪頭想了一會兒,好像發現了什么。他說,六層的金字塔形積木,需要更大的底座來支撐整個高度,雖然高度上增加了三層,但用到的積木,可能比20多塊多吧?我問他,那你猜會需要幾塊呢?他說,也許六層的需要40多塊,九層的需要90多塊吧。
到底非非的猜測靠不靠譜呢?動手驗證一下就好呀。
六層的金字塔形宇宙飛船,非非花了好一陣功夫才搭完。他反復數了兩遍,驚訝地發現,這個看上去不太大的家伙,居然花掉了91塊積木——和他猜測的40多塊積木相差甚遠。九層宇宙飛船的建造難度和用料數量,就更加超出非非的預期。我們在客廳地板上搭了很久,直到耗盡了家里所有的立方體積木,也沒能最終完成,因為九層飛船總共需要285塊積木。
大人們可能對這種數字小把戲不以為然——這不就是乘方運算在起作用嗎?一年級的小孩子又沒學過乘方,當然搞不清其中的規律了。其實,這件事真的與我們所處的年齡段無關,因為很多人終其一生,還總是會在類似的地方犯錯誤,或總是選擇性地相信主觀經驗、拒絕科學邏輯。
古代世界七大奇觀之一的羅得島太陽神銅像,是由當時的著名雕塑家林多斯的查爾斯(https://en.wikipedia.org/wiki/Chares_of_Lindos)設計的。據傳,當時羅德島人曾問查爾斯,如果雕像高50英尺,需要多少建造經費。查爾斯回答了一個數字。羅德島人追問道,如果我們把雕像造得更大,高度達到100英尺,需要多少錢呢?查爾斯非常自信地說,高度增加了一倍,經費也增加一倍就行了。
查爾斯對建造經費的預估,與六層的金字塔形飛船需要多少積木,難道不是一模一樣的問題嗎?很不幸,擅長雕塑的查爾斯并不擅長科學思維,或者說,他和非非一樣更習慣從表象出發而不是從科學規律出發想問題。在傳說中,林多斯的查爾斯的結局是悲劇性的——他在實際建造過程中發現工程花費遠超預算,他無法面對羅德島人,更無法面對自己作為最好雕塑家的名譽,在雕像完工前就自殺身亡。
有一次我們在天津港玩的時候,正好遇到兩艘豪華郵輪就近停靠,一艘是歌詩達郵輪大西洋號,另一艘是皇家加勒比郵輪海洋量子號。朋友中有人事先從官網查到了兩艘郵輪的信息——大西洋號排水量86000噸,海洋量子號排水量167800噸。也就是說,海洋量子號的重量大約是大西洋號的兩倍。抵達天津港前,朋友們紛紛猜測,港口中停靠的兩條大船在視野中的尺度一定相差懸殊。哪料到,真到港口一看,兩條船的大小其實也差不了多少嘛。視野中,兩條船的比例關系大致如下圖所示:
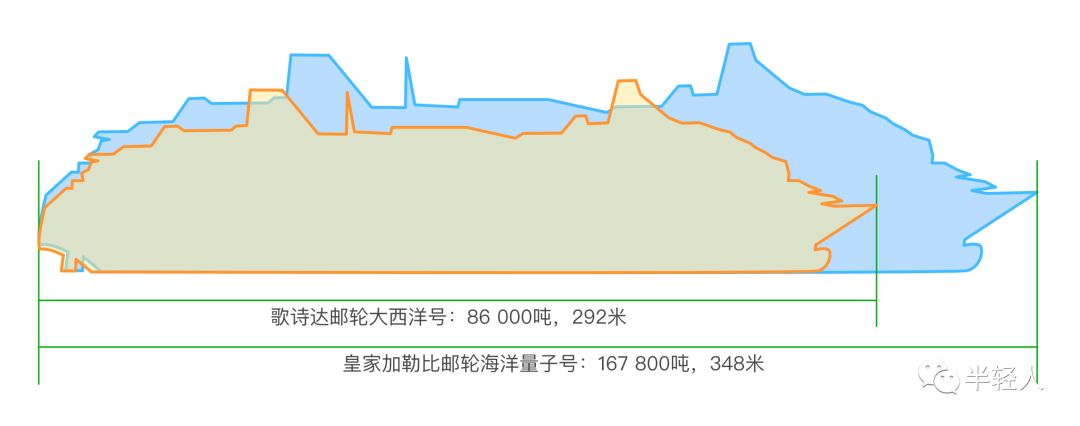
為什么體重相差懸殊的兩條船在尺寸上的差距并不明顯?這件事在原理上與我和非非建造三層、六層或九層的積木飛船也是一模一樣的。三維物體在體積或重量上的兩倍之差,反映到一維尺度上,通常就只有大約1.26:1的差距,因為:

顯然,并不是每個大人都能在需要理性推理的時候想起乘方規律,而忘掉主觀經驗的。從這一點上說,非非在估計積木數量時所犯的錯誤,大人們也很難避免。
除了體積和長度的關系,大尺度的空間距離也比較難于通過主觀經驗來認知。小朋友生活中接觸的距離單位,通常只是米、公里等等。一旦距離尺度擴展到天文單位,小朋友往往就很難想清楚,到底某個東西有多大,或到底某個東西有多遠。
每逢農歷十五,非非常指著天上說,月亮離地球好近呀。我說,月亮離地球的平均距離有38萬公里呢。這時非非就會問,38萬公里有多遠呀?是有好幾個中國到美國那么遠嗎?我說,嗯,不止有好幾個,大概好幾十個那么遠吧。非非接著問,那,地球到太陽的距離,就有好幾百個中國到美國那么遠了吧。我說,那可不止,地球到太陽的距離,足有一萬多個中國到美國那么遠呢。非非總是稍顯困惑地說,一萬多個中國到美國那么遠……那……到底有多遠啊?
一二年級的小朋友對數量級的概念還相對模糊,要弄清一個特別大的數字到底有多大,或者弄清一個特別小的數字到底有多小,對他們來說絕對是一件挺有挑戰的事兒。經常見到幾個小朋友互相比誰說的數字更大(其實是小朋友間的一種“吹牛”游戲):有的說,一百最大;有的說,一萬比你的一百大;有的說,一萬萬最大;有的說,一萬萬萬比一萬萬還大些……
其實,小朋友不容易搞清楚一萬到底比一百大多少,大人也未必能準確理解一光年比一個天文單位遠多少。這其實也是我們的主觀經驗在作怪。我們在日常生活中感知的數字尺度,遠無法覆蓋天文學上常見的尺度關系。但這并不意味著我們不能利用簡單的游戲,幫小朋友培養正確的尺度或數量級的概念。
我和非非曾用樂高積木作為基本道具,玩宇宙飛船飛越太空的小游戲。一個樂高1x1標準積木塊的長、寬大約是8毫米(參見https://en.wikipedia.org/wiki/Lego)。我和非非就將8毫米的尺度,稱為一個“積木單位”。
假設地球的大小(直徑)是1積木單位,那么,月亮離地球有多遠呢?利用地球平均直徑12742公里和地月平均距離384401公里之間的比例關系,很容易計算出,地月平均距離是30積木單位。我和非非一起在桌上擺了30個樂高積木。現在,從地球到月球的距離尺度就一目了然了:
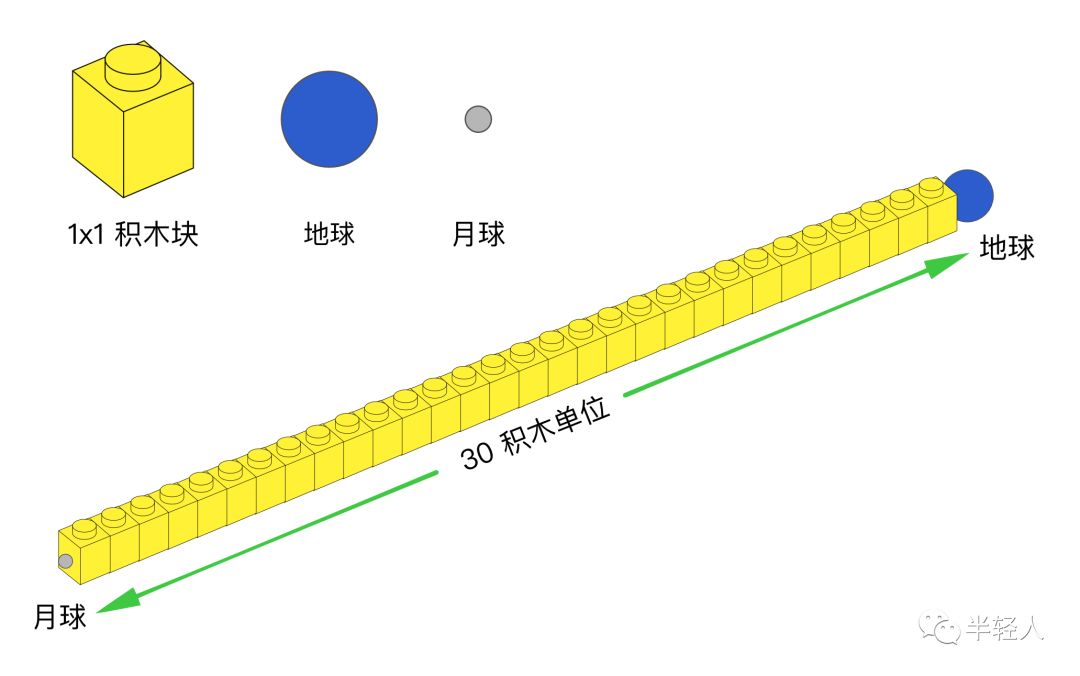
類似的,如果地球的大小(直徑)是1積木單位,那么,在我和非非的積木度量體系里,太陽該有多大呢?簡單的計算可知,太陽的大小應該是109積木單位。我們把一個1x1樂高積木放在桌子上,然后在旁邊堆砌起109層的“樂高塔”(因為太高,很難用1x1的積木垂直堆疊,實際上可以考慮用2x3或2x4的積木塊交錯堆砌成高塔的形狀),來直觀地感受地球和太陽之間的“高度差”:
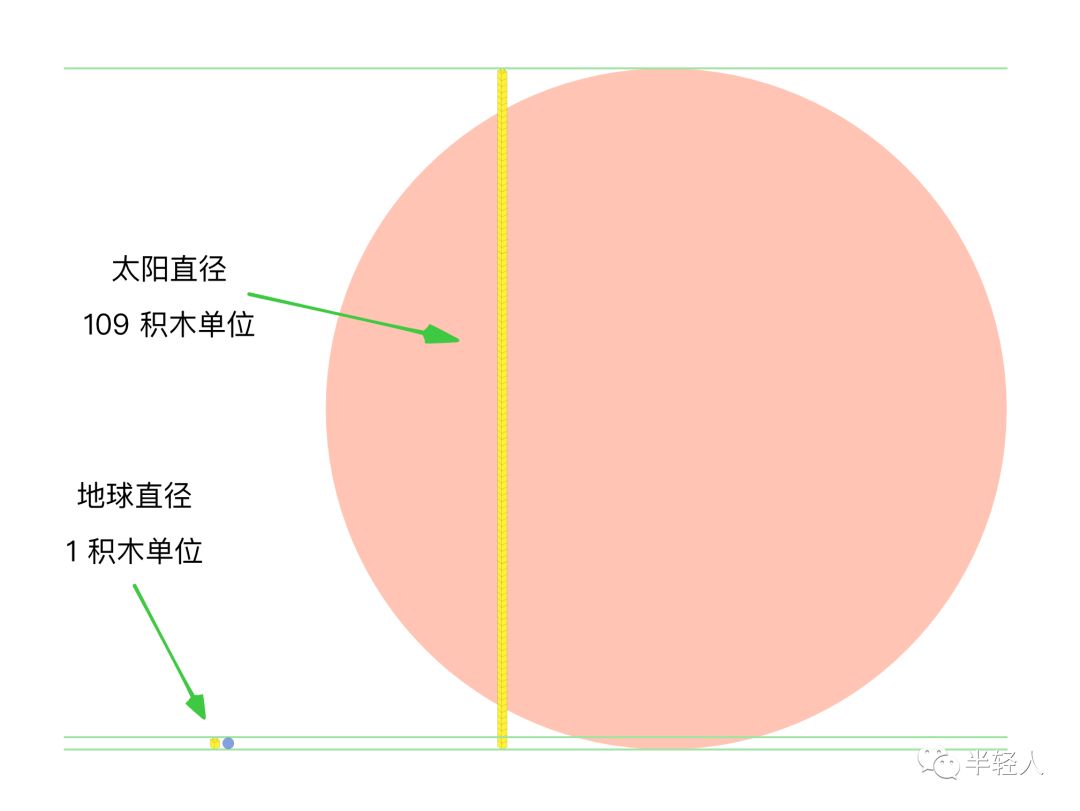
那么,在我們的積木度量體系里,地球與太陽之間的距離有多遠呢?計算可知,大約是11700積木單位。1積木單位是8毫米,11700積木單位大約是94米遠。為了直觀地體驗這個距離,我跟非非在樓下小區院子里玩的時候,會讓非非手中拿著1x1的積木塊表示地球,然后指著院子另一頭的一個小朋友對非非說,你看,這個院子縱向的長度(我們的小區比較狹長)差不多100米,站在那一頭的小朋友身高大約1米。如果你手上的積木塊是地球,那么,太陽大約就在那個小朋友所站的位置,而太陽的大小就和那個小朋友的身高差不多。非非對這個距離尺度特別驚訝,因為太陽和地球之間的距離比他的想象遠很多。他興奮地舉著積木,模仿地球一邊自傳,一邊繞著大約100米開外的“太陽”公轉——當然,他轉不了很遠,因為這個公轉圓周已大大超出了小區院子的狹窄邊界。
用積木建造金字塔飛船是為了讓小朋友體驗數學規律與經驗認知的關系,而用積木來度量星球的大小或距離則是為了讓小朋友體驗天文尺度與經驗認知的差別。兩個游戲看似不同,但本質上都是為了幫小朋友建立正確的科學常識,培養從科學視角觀察世界的好習慣。
理解信息與計算:自制二戰水準的密碼機
我們家小朋友非非喜歡聊歷史、聊戰爭。二戰時的著名戰例、著名武器,還有二戰前后的科技發展,他都特別著迷。大概是因為看到中途島海戰紀錄片里提到了美國破譯日軍密碼的故事,非非有段時間就特別關心二戰時有線、無線通訊的加密與解密。于是,我給非非講了二戰時德國人設計、制造當時最復雜的加解密工具——恩尼格碼密碼機(https://en.wikipedia.org/wiki/Enigma_machine)的故事。
以二戰時的標準來看,恩尼格碼密碼機的設計、制造簡直就是機械式信息處理機的巔峰之作。非非特別喜歡對著歷史照片,端詳恩尼格碼密碼機里設計巧妙、制作精密的鍵盤、轉子、反射器、接線板:
最重要的是,恩尼格碼密碼機的設計思路體現了很多信息學、計算機科學的基本思想。雖然通用計算機在二戰時尚未問世,但今天在程序設計中使用到的很多基本邏輯、基本方法,其實都可以在恩尼格碼密碼機找到對應的設計。我覺得,從最簡單的加密解密入手,不但可以跟孩子一起玩“軍事情報大戰”的游戲,還可以讓孩子在玩耍中,逐漸熟悉數據、指令、編碼、解碼等現代信息學和計算機科學要素。
我和非非的“軍事情報大戰”游戲從最最簡單的替換密碼開始。我們要加密的情報是一個手機號碼。非非很清楚,中國手機號碼是由11位十進制數字組成的,每一位數字有0~9總共10種可能性。所謂替換密碼,就是用一個密碼本,將待加密的每一位數字,都替換成另一個數字。這個密碼本其實就是一個一一對應的小表格,比如,把0替換成3,把1替換成2,把2替換成6……解密的時候,就用完全相反的過程,先把密碼本翻轉過來,變成一個解碼表,然后從加密后的電話號碼里,查找每一位密文對應的原始數字是多少。
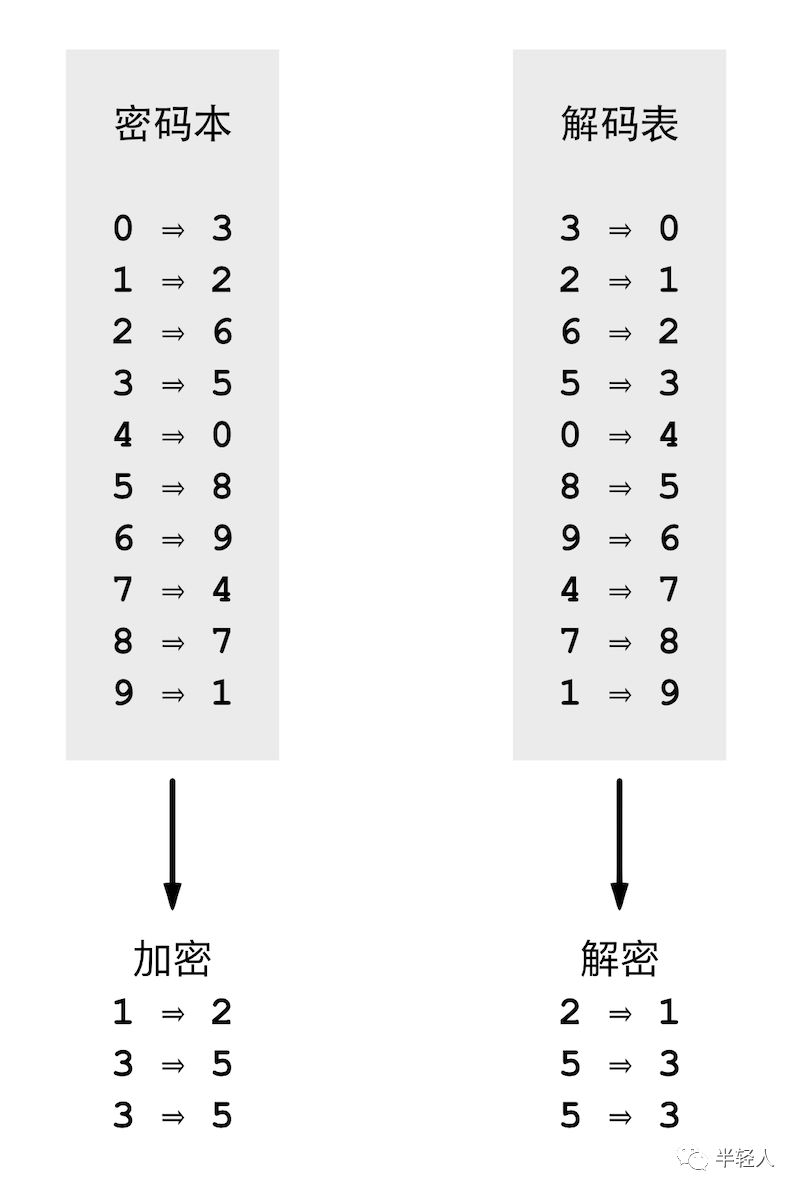
非非很快就掌握了制作這種密碼本的方法。上圖是非非制作的很多個密碼本中的一個。當加密一個“133xxxxxxxx”的電話號碼時,先查密碼本,比如得到“133”對應的密文是“255”,然后非非把加密后的數字寫在紙上,封裝在信封里,神秘兮兮地假扮成戰地通訊兵送給我解密,我拆開信封,查解碼表得到原文“133”。
替換密碼非常簡單,在大多數情況下也很容易破解。但是,與小朋友玩替換密碼的目的不在于真的加密一份情報,而是讓小朋友潛移默化地理解以下幾個信息學和計算機科學的基本概念:
信息可以用不同的編碼方法來表達。有時候,簡單變換編碼方法(比如用字符“3”表示十進制的“0”)在效果上就是一種加密。
用某種編碼表達的一份信息,可以被送給一個處理信息的人(比如上面游戲中負責加密信息的情報員),也可以被送入一個處理信息的機器(比如密碼機或通用計算機),這份信息可以被稱為“輸入信息”。
人或機器可以用特定的“操作”對信息進行處理(比如上面游戲中的加密和解密操作)。
處理后的信息,可以用特定的編碼方式呈現或顯示出來(比如上面游戲中經過加密的“密文”或經過解密的“明文”)。
現代計算機在本質上就是一臺讀取信息、處理信息再輸出信息的通用機器。
玩了幾次替換密碼,非非并不滿足。他不停追問,恩尼格碼密碼機肯定不會這么簡單吧?當然,德國人設計的軍用恩尼格碼密碼機雖然屬于替換密碼的一種實現方式(多表替換密碼,Polyalphabetic cipher),但復雜度遠遠超過我和非非玩的簡單加解密游戲。不過,要理解恩尼格碼密碼機的實現原理也不算很難,用紙板、剪刀和筆,其實就可以動手制作一個簡化版的恩尼格碼密碼機。
首先,恩尼格碼密碼機里有一個關鍵部件——反射器。“反射”在這里的意思就是將要加密的字符每兩個一對兒地連接在一起,互相作為對方的密文或明文。這樣做的好處是,加密和解密可以用完全相同的操作,查詢完全相同的“密碼本”——事實上,二戰時使用恩尼格碼密碼機的操作員,無論為原文加密,還是為密文解密,都會按照密碼本的約定設置好當天的接線板、轉輪位置等,然后直接在鍵盤上輸入原文或密文,并從指示燈中讀出相應的密文或原文。
反射器的原理可以用一個數字紙盤和一個外接圓環來簡單模擬。如下圖所示,中央白色圓盤上的數字0~9在外圈藍色圓環中被兩兩連接在一起。初始狀態下,0與3的連接既可以表示原文“0”對應于密文“3”,也可以表示原文“3”對應于密文“0”。白色的中央圓盤和外圈的藍色圓環組成了一個最簡單的反射器,同時也定義了初始狀態時的密碼本。
恩尼格碼密碼機的一個復雜之處在于,每加密一個字符,密碼本都會變化一次,這種變化,可以由字母轉輪的轉動來實現。回到上圖中圓盤和圓環的例子,我和非非用紙板剪成圓形,組裝成上圖的樣子,中央圓盤可以旋轉。這時,當我們在初始位置對第一個字符進行了加密(比如將“1”加密成“5”)后,中央圓盤就必須順時針旋轉一格。旋轉后,外圈圓環定義的反射關系,就變化成了另一種方式。我們在這個狀態下,將電話號碼的第二個數字“3”加密成“1”。下一步,中央圓盤再轉一格,這時要加密的電話號碼第三個數字雖然還是“3”,但加密結果已經變成了“9”。——每加密或解密一個字符,密碼本就變化一次,這其實就是恩尼格碼密碼機的精髓所在了。
真實的恩尼格碼密碼機使用了多個轉輪,這增加了密碼本的復雜度。我和非非的“紙板密碼機”其實也可以模擬多個轉輪的情況。下圖展示了我們在中央白色圓盤和外圈藍色圓環之間,多引入了一個綠色轉輪后的樣子。綠色轉輪上,我和非非畫了一些或直接連接,或交叉連接的線條,把中央圓盤的數字和外圈圓環的線路端點連接起來。這樣一來,從中央圓盤的一個數字出發,通過綠色圓環,再通過藍色圓環,然后依次返回到另一個數字,整個路徑變得大為復雜。每次加密一個字符后,中央圓盤就順時針轉動一格,這時,每兩個字符之間的連接或對應關系就與上一個位置大為不同。為了增加復雜度,夾在中間的綠色圓環也可以在特定時候轉動——比如,中央圓盤每轉動10次,綠色圓環就轉動1次。
基于我們的“紙板密碼機”,如果把10個數字擴展到A~Z的26個字母,再把綠色圓環從1個擴展到3個、5個或更多,其復雜度就和二戰時德國人使用的恩尼格碼密碼機差距不大了。
恩尼格碼密碼機利用轉輪和連線組成動態變化的密碼本,這個技巧讓非非小朋友大呼神奇。能夠在紙板上簡單重現恩尼格碼密碼機的實現原理,對喜歡歷史也喜歡科技的小朋友來說,是非常有趣的體驗。當然,最重要的還是要讓小朋友在這個游戲的過程里,親自感受信息處理的基本邏輯。經過了這樣的游戲體驗,未來小朋友肯定更容易理解 “數據” “指令” “編碼”“解碼”等概念。
信息檢索的奧秘:搜索引擎角色扮演
自從在學校里學過拼音并能用鍵盤輸入漢字之后,我們家非非就經常在谷歌或百度上搜索他喜歡的信息,比如蜥蜴有多少種,戰列艦有幾門主炮,古代青銅器上的花紋長什么樣,最早的個人電腦和今天的電腦有何不同,等等等等。搜索得多了,非非有一次就好奇地問我,谷歌和百度這樣的搜索引擎,到底是如何在那么短的時間里,找到許多許多信息的?
這真是一個好問題!非非雖知道我曾在谷歌工作過很多年,也去谷歌總部和谷歌北京的辦公室玩耍過,可他此前并不太清楚谷歌到底是做什么的。他能一邊使用搜索引擎,一邊主動提出關于搜索引擎的問題,這還真是讓做過很多年搜索相關算法的我大為感動呢。
當然,感動歸感動,到底該如何向七八歲的小朋友科普搜索引擎知識呢?到底是具體的搜索算法更重要,還是人類數千年來摸索的信息組織和管理思想更重要?有沒有可能通過一個好玩的游戲,讓小朋友自己來了解組織信息的基本手段?
我和非非拿出白紙,開始玩一個“搜索引擎角色扮演”的小游戲。我把白紙裁成8片,讓非非在每片紙上寫一個編號。我將每片紙稱作一個“信息盒子”。然后,我在每個信息盒子里,用英文字母寫上不同的信息,比如1號盒子里是“A”“B”“C”,2號盒子里是“C”“D”……如下圖:
這時,我讓非非扮演一個“搜索引擎”。非非心領神會,立即張開嘴巴,用手勢示意,他的嘴巴就是搜索框,現在可以開始搜索了。作為用戶,我提了幾個從簡單到復雜的搜索需求,分別是:
字母“F”在哪些信息盒子里出現過?
字母“A”在所有這些信息盒子里一共出現了多少次?
字母“A”和字母“B”同時在哪些信息盒子里出現過?
有沒有哪個信息盒子同時包含了字母“A”、字母“C”和字母“E”?
對于這幾個搜索問題,非非很快就找到了雖然笨拙、但肯定奏效的解決方案。他針對每個問題,都會從編號1到編號8,一個接一個地查看每個信息盒子里的信息,然后給出答案。
我問非非,如果按照你這種方式來實現搜索引擎,你覺得會有什么問題嗎?非非回答,這樣做太慢了,每次都要把所有信息盒子看一遍,如果信息盒子特別多,那要花多少時間啊。
我問非非,你用谷歌或百度時,輸入一個查詢,谷歌和百度回答你的速度有多快?非非說,特別快,幾乎是一眨眼的時間。谷歌和百度一定不會像我一樣每次都把所有信息盒子看一遍。
顯然,真正的搜索引擎使用的是更聰明的方法。小朋友一旦意識到了這一點,自然就提起了極大的興趣,非要刨根問底弄清楚。于是,我開始教非非如何為已有信息建立“倒排索引”。
我跟非非講,搜索引擎建立索引的做法其實特簡單,只是將原來的信息變換了一種組織方式。剛才我們看到的信息,是以每個信息盒子為單位的。為了更快地完成搜索,我們需要換一種信息的組織方式,即,我們從每個字母的角度出發,先創建一張表格,記錄下每個字母到底在哪些信息盒子里出現過。這個表格的每一行對應一個字母,字母后面記錄的是一組信息盒子的編號,表示這個字母在哪些信息盒子里出現過。如果一個字母在某個信息盒子里出現過兩次,就把信息盒子的編號記錄兩次。倒排索引的建立方法不算難,非非很快就在紙上完成了倒排索引的編制:
利用倒排索引,稍加提示,非非快速掌握了搜索的技巧。要想搜索某個字母在哪些盒子里出現過,只要直接讀出倒排索引中該字母對應的那一行就可以了。要想搜索某個字母在所有盒子中出現過幾次,只要數一下該字母對應的編號個數就可以了。要想搜索某兩個字母在哪些盒子里同時出現過,我們需要歸并兩個字母對應的編號序列,找出在兩個序列里同時出現的那些編號。
玩了幾次搜索引擎角色扮演的游戲,非非好像恍然大悟似地說,我知道了,原來把信息編制成索引,就可以又準又快地查找信息。那么說,我們上學時查的《新華字典》,其實也是一種索引啦,因為可以從一個字查到這個字的意思。確實,《新華字典》本身就是按拼音順序編排的一種索引結構,雖然有別于搜索引擎的倒排索引,但也屬于信息的一種有序組織方式。相比之下,專業書籍在書后所附的關鍵詞索引,在功能上更接近搜索引擎一些。
陪孩子玩搜索引擎游戲,其實只是想讓小朋友弄明白:
信息的組織方式可以有很多種。
有序的信息組織,可以大幅加快信息檢索的速度。
搜索引擎的基本原理是用計算機來重新組織信息,并通過對索引的查詢完成快速檢索。
非非很快就把這種重新組織信息的技能舉一反三,用在他熟悉的各種地方。比方說,他剛背過《道德經》開頭幾句。他發現,假設把每一句裝進一個有編號的信息盒子,就可以用每個單字作為索引入口,建立起單字到句子編號的倒排索引,就像下圖這樣:
不過,玩搜索引擎角色扮演游戲也有一個副作用:非非小朋友對爸爸曾經在谷歌做的工作,徹底失去了神秘感。非非說,原來爸爸在谷歌做工程師,就是在開發這么一個程序呀。說這話的時候,非非一臉不屑。
要讓非非對谷歌、百度之類現代搜索引擎的實現復雜度有一些認知,其實也不算太難。這部分得益于前面我們介紹過的“積木游戲”,即,如何讓小朋友熟悉比較大的數量級或真實尺度。
我還是拿人工編排和使用倒排索引作為示例,跟非非一起討論:一個小朋友最多可以為多少個信息盒子(或者說,多少要檢索的網頁)建立并管理索引?非非的猜測是100個。我接著告訴非非,根據公開數據估計,谷歌索引的網頁數量,大概在幾十到幾百萬億的樣子。既然每個人可以管理100個網頁的索引,要想全部用人工來管理谷歌的所有網頁,恐怕需要約一萬億人(這遠遠超出了地球上人類的總人口,有必要從鄰近的外星球上把外星人也請過來)。
現在,假設我們有了足夠多的可以建立和管理索引的人,我們的搜索引擎該如何建設呢?
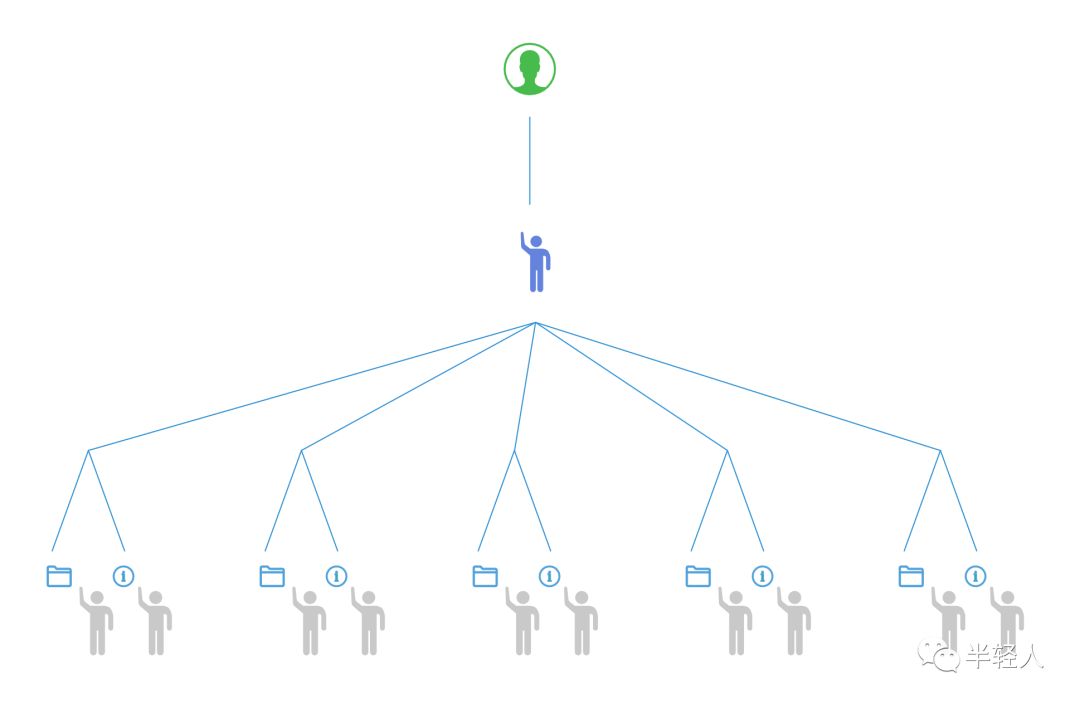
上圖中,綠色頭像代表搜索引擎的用戶。灰色小人代表我們請來的一萬億人類與外星人志愿者大軍,他們也被稱為“工人”(Worker)。我們可以把工人分成兩組,一組人專門建立和處理索引,一組人專門管理原始的信息盒子(網頁),這兩組工人既可以兩兩搭檔工作,也可以分別在各自的大組中工作。這時,因為志愿者太多,我們不得不請來一名或多名“指揮官”(Master),見圖中的藍色小人。搜索引擎用戶提出的搜索請求,要先發送給指揮官,然后再由指揮官分發給每個工人,工人根據自己管理的網頁或索引,完成一部分搜索任務后,直接將結果返回給指揮官。一旦指揮官收到了所有工人返回的結果,就會將結果合并、去重、排序,然后返回給用戶(注:這里對分布式索引和檢索系統的Worker和Master工作原理的講解僅為簡化后的示意,與真實系統有較大差別)。
指揮官和工人的比喻,非非大概只能理解個皮毛。但通過這樣的講解,非非還是可以約略知道,原來爸爸在谷歌時所寫的程序,并不似想象中那么簡單。重要的是,這樣的講解可以在非非心里埋下一顆將復雜任務分而治之的種子,這種子將來發芽長大時,小朋友與現代計算機科學里最重要的概念之一——分布式計算——之間就沒有太多隔閡了。
少談教育,多玩游戲
上一篇《AI時代,提高孩子創造未來的能力,陪孩子玩什么游戲?》內容稍雜了一點,既有訓練邏輯思維的游戲,也有訓練語言能力、表達能力乃至創造力的游戲。這一篇作為續篇,我只介紹了與科學認知、信息學和編程邏輯這三方面相關的小游戲。接下來,我還是會不定期地把我和非非常玩的游戲記錄下來,以續篇的形式發出,但每個續篇會有不同的側重方向——也許,下一篇可以集中討論語言和表達能力?
有人質疑我寫的這些游戲的可操作性和可復制性。比方說,有人就問過我,你這些游戲看上去挺好,但如果家長的數學不好或編程不好,該怎么陪孩子玩,怎么引導孩子呢?你有沒有類似教學大綱或教學參考書之類的東西?
很遺憾,我既不知道類似問題的答案,也沒有教學大綱或教學參考書。
我把我與非非小朋友常玩的,有關邏輯思維訓練或科學認知訓練的游戲記錄下來,只是想和大家分享這些有趣的經歷。我不是教育學家,不知道該如何將教育方法變成任何人都很容易獲取的“用戶手冊”。另一方面,我也不愿看到有趣的游戲搖身變成枯燥、呆板的條條框框。
這個世界已擁有太多的程式化教育,何必再添一門讓小朋友皺眉的乏味功課呢?
孩子們能從游戲里感悟、領會到有趣的知識,學到有用的思維方法,當然最理想不過。但就算孩子只能體會到游戲本身的快樂,這快樂又何嘗不是一種珍貴的童年記憶呢?
游戲就是游戲——讓我們少談教育,多玩游戲。
-
AI
+關注
關注
87文章
31433瀏覽量
269832
原文標題:AI時代,提高孩子創造未來的能力,陪孩子玩什么游戲?(2)
文章出處:【微信號:kaifu,微信公眾號:李開復】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
芯盾時代入選ISC.AI 2024創新能力百強
NVIDIA NIM Agent Blueprint加速企業級AI應用落地
未來AI大模型的發展趨勢
AI for Science:人工智能驅動科學創新》第4章-AI與生命科學讀后感
《AI for Science:人工智能驅動科學創新》第二章AI for Science的技術支撐學習心得
嵌入式系統的未來趨勢有哪些?
平衡創新與倫理:AI時代的隱私保護和算法公平
羅杰·瑞迪:AI能力已遠超我們人類
科普講座 | 讓AIGC提高你的專業表達和創作能力





 AI時代到來 如何提高孩子創造未來的能力
AI時代到來 如何提高孩子創造未來的能力















評論