作為ICT的從業人員,大家都知道有兩個公司是有點臭名昭著,因為他們和SUN Micro公司不一樣,好IT公司養工程師,“壞”公司養律師。Qualcomm和Oracle都是以律師而著名。最近特別是Oracle,更加不養中國的工程師了。
在memory界,也有一個公司有類似的名氣,那就是Rambus。在2019年的Memory+的會議上,他們居然吃了豹子膽,給自己挖了一個深深的坑,《Big Data, AI and the future of Memory》。對于AI來講,目前從應用,到框架,再到底層語言和硬件,這是一個百家爭鳴的時代。Nvidia在鞏固了自己在訓練上的地位之后,向推理進攻,各家初創公司在利用開源框架,占領推理市場,并伺機向訓練進攻。[1]
因此,對于任何一種神經網絡來講,實現對于資源的需求的影響還是比較大的,一個神經網絡在不同的框架(Caffe/Pytroch/TensorFlow)上,在不同的硬件平臺上(CPU/GPU/FPGA/ASIC)的需求都多多少少不同。更不要講有成千上萬的AI煉丹師在各種調參,生成各種定制的網絡,因此Rambus這種行為和我今天一樣都是一種“無知者無畏”的行動。
從2015年的Resnet之后,大家都認為在神經網絡的深度學習方面,特別是標桿性的ImageNet的上,大家沒有太明顯的進展了。[2]
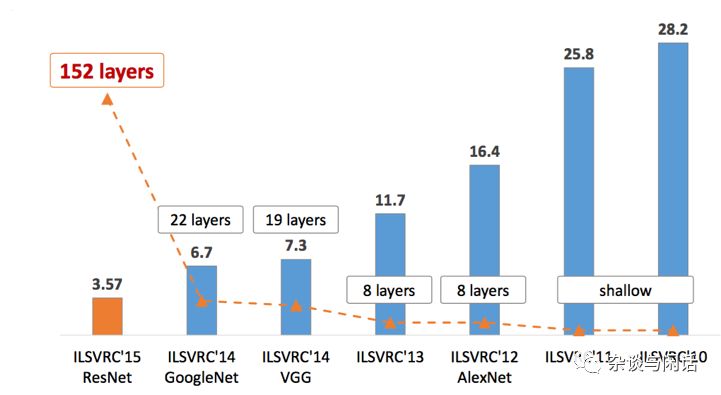
因此從2012年以來的ImageNet優勝網絡模型來看,大家的趨勢很明顯,Top-5的錯誤率逐年下降,網絡的層數也越來越厚。當然還有就是網絡的parameter,也就是weight和bias 也越來越多。
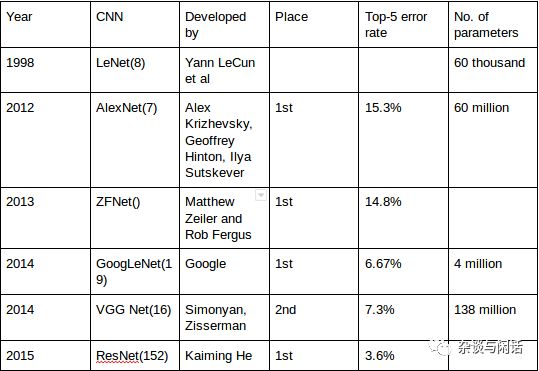
計算和I/O是目前占主導地位的馮氏體系的核心,和之前在2018年流行的爭論一樣,“深度學習的進步是(看上圖,YannLeCun的10位數識別是1998)因為算法的進步,還是算力的進步”,計算和I/O的那個作用大也是一個“雞蛋問題”。
很有意思的是,很多東西拋開現象看本質會有一個別樣的視角。舉個上周學習到觀點,對于數據庫領域來講,目前workload就是OLTP和OLAP。OLTP的交易的本質就是數據的I/O,對!就是把你的軟妹幣從你口袋中搬運到淘寶賣家的口袋中去。OLAP的本質就是計算,在知道你買了尿布,奶粉之后算出來應該給你推送嬰兒車的廣告。
那對于目前比較流行的深度學習來講,也可以從同樣的話來總結。基于卷積計算的CNN,他的本質就是計算,也算出你到底有多少個預先訓練好的元素,這些元素包含形狀,顏色等等。比如,如果你有一個嘴巴,兩個眼睛,和一個鼻子,那就是一個人臉。
還有一種是RNN,RNN的本質也是計算和I/O,和CNN的計算上線文無關,RNN的具體的表現形式為網絡會對前面的信息進行記憶并應用于當前輸出的計算中。當初,Google不顧版權協會的反對,數字化人類的書籍,本質上就是理解大家的語言。比如在天朝,如果有一個名詞,開始是“歷害”,大家肯定知道下一個就是“國”了。
因此,不過CNN和RNN,大家都是需要參數了,也就是“Weights” 和“Bias” 。兩者對于這些參數的share的方式也很大不同。
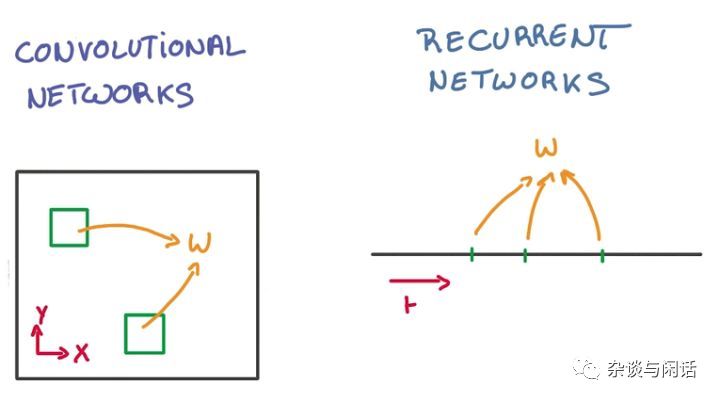
CNN是在空間上共享,RNN在時間上共享。因此,問題就來了,這些參數是怎么出來的呢?他們的大小和性能的要求是多少呢?
先來講對于大小的要求。這里就要從最基本的CNN網絡 Alexnet說起。
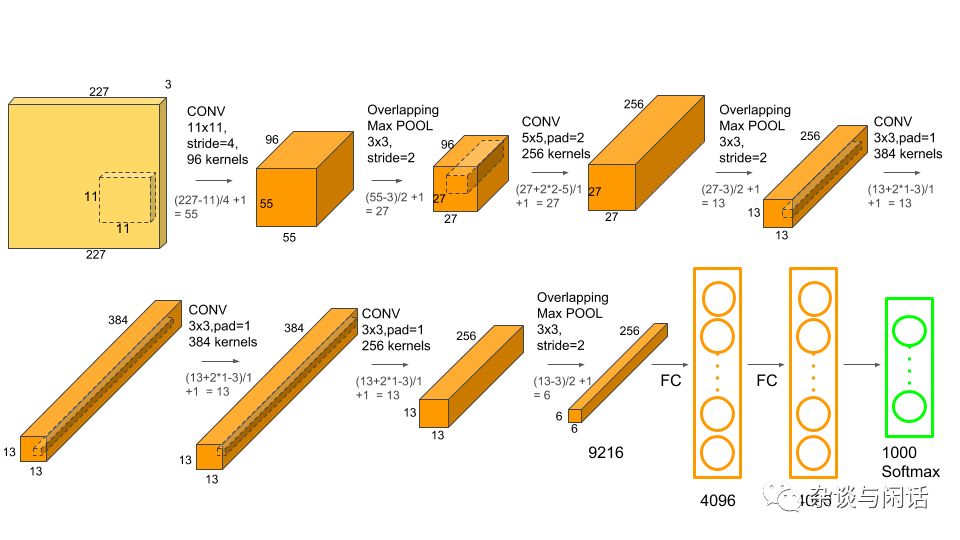
仔細介紹每一層的東西:(對于stride 和padding不熟的,請看CS231n,不知道CS231n的,請打賞,并到此為止)
input:彩色的圖片 227X227X3
Conv-1:第一層的卷積有96個kernel。kernel的大小是11X11,卷積的stride是4,padding是0
MaxPool-1 :第一層卷積的最大值。Pooling的size是3X3,stride是2
Conv-2:256個kernel,kernel的size是5X5,stride是1,padding是2.
MaxPool-2:第二層卷積的最大值,Pooling是3X3, stride是2
Conv-3: 384個kernel。kernel大小是3X3, stride是1 ,padding是1.
Conv-4:和第三層類似。384 個kernel。3X3,strdie和padding是1.
Conv-5:256個kernel。kernel size 3X3,stride和padding是1.
MaxPool-3:第五層卷積的最大值,Pooling是3X3, stride是2
FC-1:第一個全連接層,有4096個神經元
FC-2:第二個全連接,有4096個神經元
FC-3: 第三個全連接層,有1000個神經元
對于CNN來講,上一層的輸出是這一層的輸入。因此需要把每一層的輸出算清楚。從上面看,每一層的網絡類型有Input,Conv,Maxpool和FC四類,因此下面的計算也是按四類開始的。
O=(I-K+2P)/S+1
其中:O是輸出的寬度,I是輸入的寬度,K是Kernel的寬度,N是Kernel的數量,S是stride, P是Padding。N是kernel的數量。
因此,輸出的image的size就是OXOXN
Output的規模的計算:
Conv 層的計算:定義如下:
作死用中文解釋一下,就是一個227X277的圖上,我用11X11的小方案從左到右,從上到小描紅一邊。這個描紅,這個11X11小框子每次跳4格,如果跳到邊上沒對齊的話,我用多一行的0來補齊。因此227X227X3的第一層卷積的輸出就是:(227-11+2X0)/4+1=55. image size=55X55X96
MaxPool 的計算:定義如下:
O=(I-ps)/S+1
其中:O是輸出的寬度,I是輸入的寬度, S是stride,ps是Pool size
因此,對于第一層卷積的Maxpooling就是(55-3)/2+1=27 , image就是27X27X96
FC的計算:一個全連接層的輸出就是一個向量,這個向量的單元數是它神經元的數量。比如FC-1就是一個4096的向量。
因此,對于一個包含227X227X3的圖片,它的歷程如下:
一開始是227X227X3,過了第一層卷積,就是55X55X96, 之后的MaxPool就是27X27X96. 第二次卷積之后是27X27X256,之后的MaxPooling就是 13X13X256,第三層卷積是13X13X384,之后的第4和5 卷積變成:27X27X256,第3個Maxpooling 變成 6X6X256,之后的FC-1就是4096X1,FC-2不變,最后就是一個1000X1 的向量了。
-
神經網絡
+關注
關注
42文章
4776瀏覽量
100948 -
大數據
+關注
關注
64文章
8899瀏覽量
137578
原文標題:大數據、AI和存儲芯片的未來
文章出處:【微信號:SSDFans,微信公眾號:SSDFans】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
劃片機在存儲芯片切割中的應用優勢

英偉達加速認證三星新型AI存儲芯片
一文帶你了解什么是SD NAND存儲芯片
存儲芯片的TBW和MTBF:關鍵指標解析與提升策略

SK海力士Q2業績創新高,AI存儲芯片銷售強勁
存儲芯片有哪些類型
存儲芯片和邏輯芯片的差異
三星電子存儲芯片漲價,AI需求激增提振業績預期





 大數據和AI以及存儲芯片的未來
大數據和AI以及存儲芯片的未來










評論