模型的訓練、調參是一項非常費時費力的工作,了解神經網絡內部的數學原理有利于快速找出問題所在。本文作者從零開始,一步一步講解了訓練神經網絡時所用到的數學過程。
神經網絡是線性模塊和非線性模塊的巧妙排列。當聰明地選擇并連接這些模塊時,我們就得到了一個強大的工具來逼近任何一個數學函數,如一個能夠借助非線性決策邊界進行分類的神經網絡。
運行代碼的步驟如下:
git clone https://github.com/omar-florez/scratch_mlp/python scratch_mlp/scratch_mlp.py
盡管反向傳播技術具有直觀、模塊化的特質,但是它負責更新可訓練的參數,這是一個一直未被深入解釋的主題。讓我們以樂高積木為喻,一次增加一塊,從零構建一個神經網絡來一探其內部功能。
神經網絡就像是由樂高積木組成的
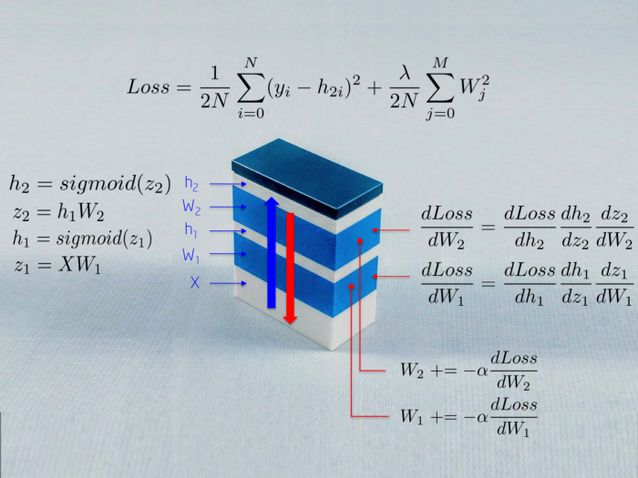
上圖描述了訓練一個神經網絡時所用到的部分數學過程。我們將在本文中解釋這個。讀者可能感到有趣的一點是:一個神經網絡就是很多模塊以不同的目標堆疊起來。
輸入變量 X 向神經網絡饋送原始數據,它被存儲在一個矩陣中,矩陣的行是觀察值,列是維度。
權重 W_1 將輸入 X 映射到第一個隱藏層 h_1。然后權重 W_1 充當一個線性核。
Sigmoid 函數防止隱藏層中的數字落到 0-1 的范圍之外。結果就是一個神經激活的數組,h_1 = Sigmoid(WX)。
此時,這些運算只是組成了一個一般線性系統,無法對非線性交互建模。當我們再疊加一層,給模塊的結構增加深度的時候這一點就會改變。網絡越深,我們就會學到越多微妙的非線性交互,能解決的問題也就越復雜,或許這也是深度神經模型興起的原因之一。
為什么我要讀這篇文章?
如果你理解一個神經網絡的內部部分,你就能夠在遇到問題的時候快速知道先去改變哪里,并且能夠制定策略來測試你所知道的這個算法的部分不變量和預期的行為。
因為調試機器學習模型是一項復雜的任務。根據經驗,數學模型在首次嘗試的時候不會奏效。它們可能會對新數據給出較低的準確率,會耗費很長的訓練時間或者太多的內存,返回一個很大的錯誤負數值或者 NAN 的預測……在有些情況下,了解算法的運行機制可以讓我們的任務變得更加便利:
如果訓練花費了太多的時間,那增加 minibatch 的大小或許是一個好主意,這能夠減小觀察值的方差,從而有助于算法收斂。
如果你看到了 NAN 的預測值,算法可能接收到了大梯度,產生了內存溢出。可以將這個視為在很多次迭代之后發生爆炸的矩陣乘法。減小學習率可以縮小這些數值。減少層數能夠減少乘法的數量。剪切梯度也能夠明顯地控制這個問題。
具體的例子:學習異或函數
讓我們打開黑盒子。我們現在要從零開始構建一個學習異或函數的神經網絡。選擇這個非線性函數可絕對不是隨機的。沒有反向傳播的話,就很難學會用一條直線分類。
為了描述這個重要的概念,請注意下圖中,一條直線是為何不能對異或函數輸出中的 0 和 1 進行分類。現實生活中的問題也是非線性可分的。
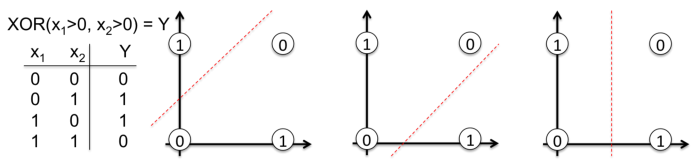
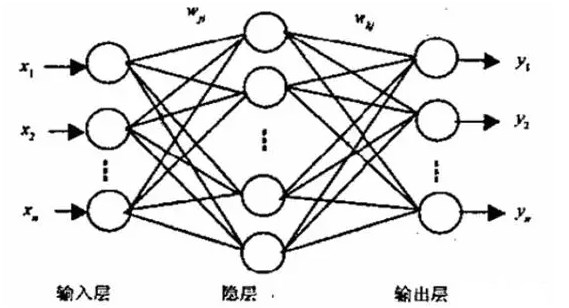
這個網絡的拓撲結構非常簡單:
輸入變量 X 是二維向量
權重 W_1 是具有隨機初始化數值的 2x3 的矩陣
隱藏層 h_1 包含 3 個神經元。每個神經元接受觀察值的加權和作為輸入,這就是下圖中綠色高亮的內積:z_1 = [x_1, x_2][w_1, w_2]
權重 W_2 是具有隨機初始化值的 3x2 的矩陣
輸出層 h_2 包含兩個神經元,因為異或函數的輸出要么是 0(y_1=[0,1]),要么是 1(y_2 = [1,0])
下圖更加直觀:
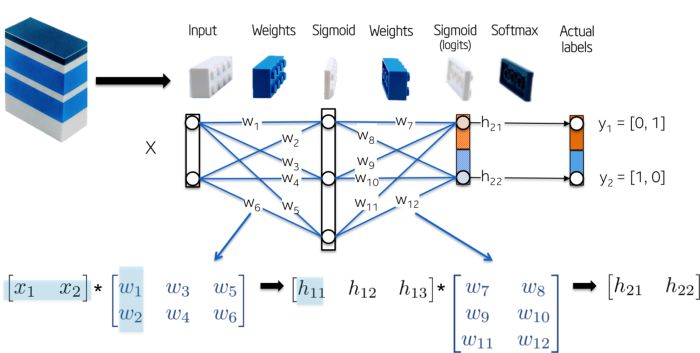
我們現在來訓練這個模型。在我們這個簡單的例子中,可訓練的參數就是權重,但是應該知道的是,目前的研究正在探索更多可以被優化的參數類型。例如層之間的快捷連接、正則化分布、拓撲結構、殘差、學習率等等。
反向傳播是這樣的一種方法:在給定的一批具有標簽的觀察值上,朝著將預定義的錯誤指標(就是損失函數)最小化的方向(梯度)更新權重。該算法已經多次被重復發現,這是另一種更通用的被稱為自動微分的技術在反向積累模式下的特例。
網絡初始化
讓我們用隨機數來初始化網絡權重
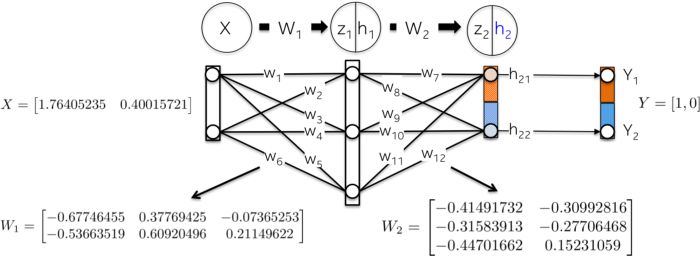
前向步驟:
這一步的目標就是把輸入變量 X 向前傳遞到網絡的每一層,直至計算出輸出層 h_2 的向量。
這就是其中發生的計算過程:
以權重 W_1 為線性核對輸入數據 X 做線性變換:
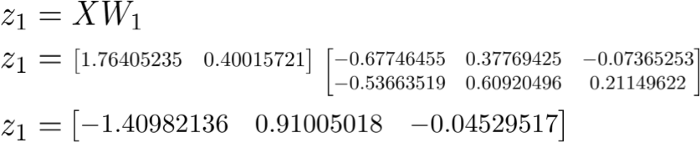
使用 Sigmoid 激活函數對加權和進行縮放,得到了第一個隱藏層 h_1 的值。請注意,原始的 2D 向量現在映射到了 3D 空間。

第 2 層 h_2 中發生了類似的過程。讓我們首先來計算第一個隱藏層的加權和 z_2,它現在是輸入數據。

然后計算它們的 Sigmoid 激活函數。向量 [0.37166596 0.45414264] 代表的是網絡對給定的輸入 X 計算出的對數概率或者預測向量。

計算整體損失
也被稱為「實際值減去預測值」,這個損失函數的目標就是量化預測向量 h_2 和人工標簽 y 之間的距離。
請注意,這個損失函數包括一個正則項,它以嶺回歸的形式懲罰較大的權重。換言之,平方值比較大的權重會增大損失函數,而這正是我們希望最小化的指標。
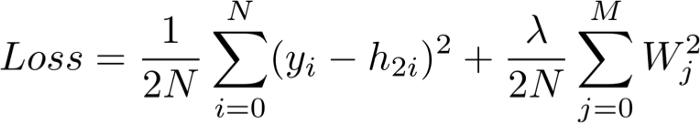
反向步驟:
這一步的目標就是沿著最小化損失函數的方向更新神經網絡的權重。正如我們將要看到的,這是一個遞歸算法,它可以重用之前計算出來的梯度,而且嚴重依賴微分函數。因為這些更新減小了損失函數,所以一個神經網絡便「學會了」去逼近具有已知類別的觀察值的標簽。這就是被稱作泛化的一種屬性。
與前向步驟不同的是,這個步驟沿著反向的順序進行。它首先計算出輸出層中損失函數對每個權重的偏導數 (dLoss/dW_2),然后計算隱藏層的偏導數 (dLoss/dW1)。讓我們詳細地解釋每個導數吧。
dLoss/dW_2:
鏈式法則表明,我們可以將一個神經網絡的梯度計算分解成好多個微分部分:
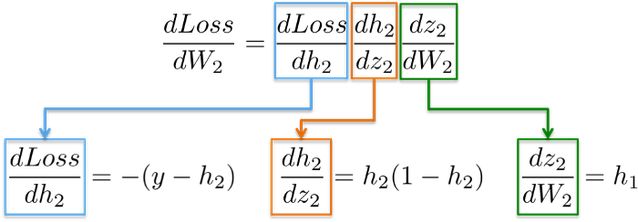
為了幫助記憶,下表列出了上面用到的一些函數定義以及它們的一階導數:
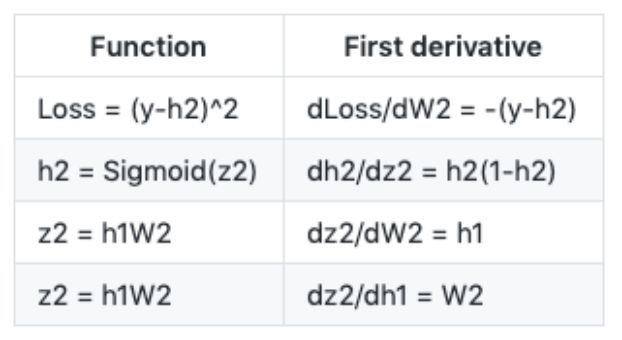
更直觀地,我們在下圖中要更新權重 W_2(藍色部分)。為了做到這件事,我們需要沿著導數鏈計算三個偏導數。
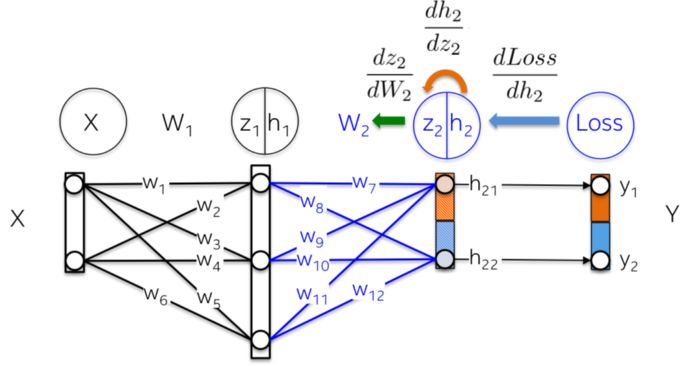
將數值代入到這些偏導數中,我們就能夠計算出 W_2 的偏導數,如下所示:
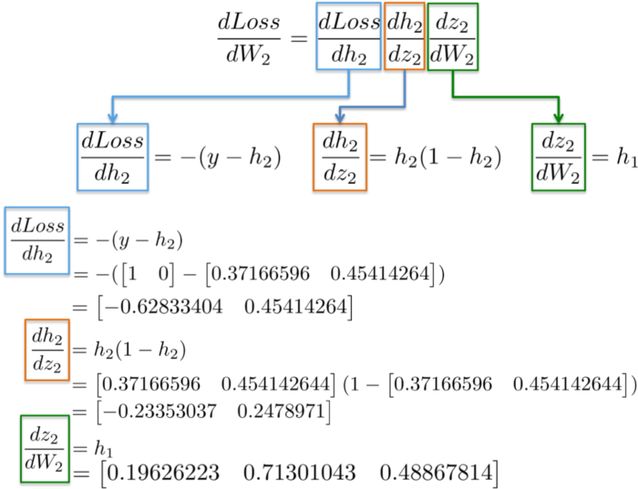
結果是一個 3x2 的矩陣 dLoss/dW_2,它將會沿著最小化損失函數的方向更新 W_2 的數值。
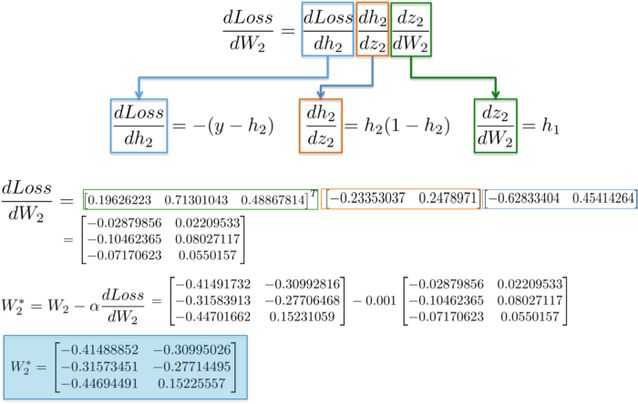
dLoss/dW_1:
計算用于更新第一個隱藏層 W_1 權重的鏈式規則就展現了重復使用已有計算結果的可能。
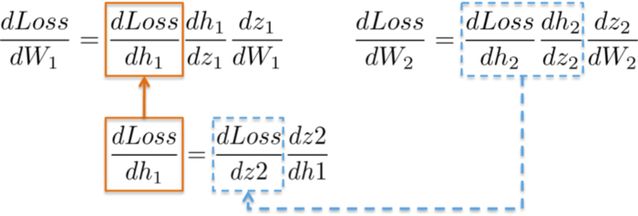
更直觀地,從輸出層到權重 W_1 的路徑會碰到在后面層中早已計算出來的偏導數。
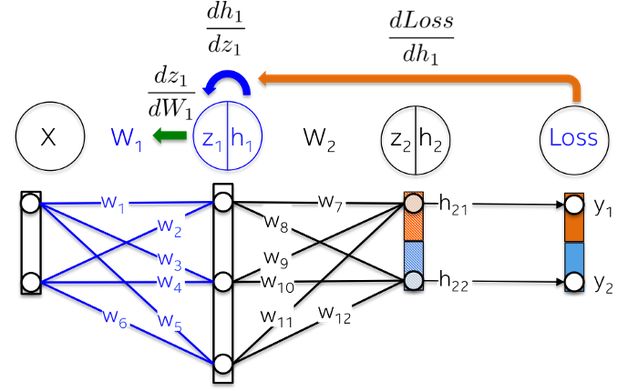
例如,偏導數 dLoss/dh_2 和 dh_2/dz_2 在上一節中已經被計算為輸出層 dLoss/dW_2 學習權值的依賴項。
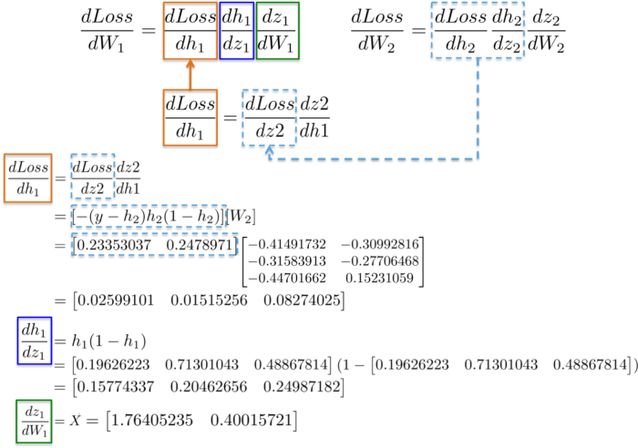
將所有的導數放在一起,我們就能夠再一次執行鏈式法則,來為隱藏層的 W_1 更新權重。

最后,我們給權重賦予新的數值,完成了對神經網絡的一步訓練。
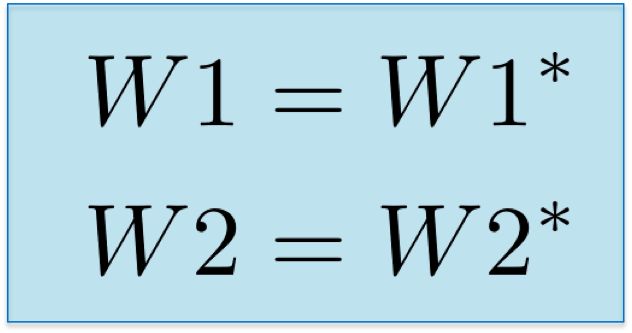
實現
讓我們僅使用 numpy 作為線性代數引擎來將上面的數學方程轉換成代碼。神經網絡在一個循環中進行訓練,其中每次迭代會給神經網絡展示標準的輸入數據。在這個小例子中,我們只考慮每次迭代中的整個數據集。前向步驟、損失函數和反向步驟的計算會得到比較好的泛化,因為我們在每一次循環中都用它們對應的梯度(矩陣 dL_dw1 和 dL_dw2)來更新可訓練的參數。
代碼保存在這個 repo 中:https://github.com/omar-florez/scratch_mlp

讓我們來運行這份代碼!
下面可以看到一些進行了好多次迭代訓練得到的能夠近似異或函數的神經網絡。
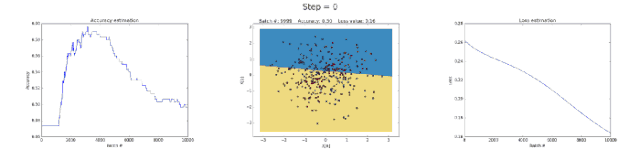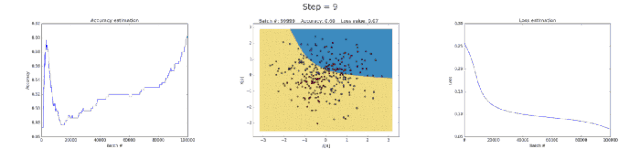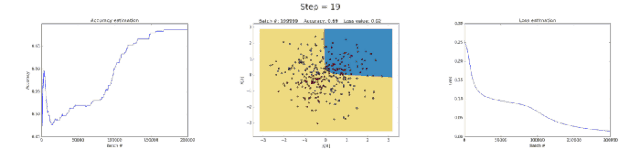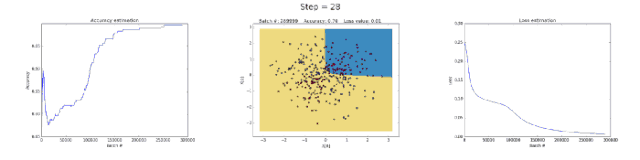
左圖:準確率;中間的圖:學習到的決策邊界;右圖:損失函數
首先,我們來看一下隱藏層具有 3 個神經元的神經網絡為何能力較弱。這個模型學會了用一個簡單的決策邊界來進行二分類,這個邊界開始是一條直線,但是隨后就表現出了非線性的行為。隨著訓練的持續,右圖中的損失函數也明顯地減小。
隱藏層擁有 50 個神經元的神經網絡明顯地增加了模型學習復雜決策邊界的能力。這不僅僅能夠得到更準確的結果,而且也使梯度發生了爆炸,這是訓練神經網絡時的一個顯著問題。當梯度非常大的時候,反向傳播中的連乘會產生很大的更新權重。這就是最后幾步訓練時損失函數突然增大的原因(step>90)。損失函數的正則項計算出了已經變得很大的權重的平方值(sum(W2)/2N)。
正如你所看到的一樣,這個問題可以通過減小學習率來避免。可以通過實現一個能夠隨著時間減小學習率的策略來實現。或者通過強制執行一個更強的正則化來實現,可能是 L1 或者 L2。梯度消失和梯度爆炸是很有趣的現象,我們后續會做完整的分析。
原文鏈接:https://medium.com/towards-artificial-intelligence/one-lego-at-a-time-explaining-the-math-of-how-neural-networks-learn-with-implementation-from-scratch-39144a1cf80
-
神經網絡
+關注
關注
42文章
4776瀏覽量
100952 -
GitHub
+關注
關注
3文章
473瀏覽量
16503
原文標題:像堆樂高一樣:從零開始解釋神經網絡的數學過程
文章出處:【微信號:tyutcsplab,微信公眾號:智能感知與物聯網技術研究所】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
脈沖神經網絡怎么訓練
怎么對神經網絡重新訓練
BP神經網絡的基本結構和訓練過程




 深度:了解訓練神經網絡時所用到的數學過程
深度:了解訓練神經網絡時所用到的數學過程










評論