基于微步驅動的開關磁阻電機轉矩脈動控制系統

一、引言

近幾年來，在伺服應用系統領域中對各種轉速的要求提高了人們對開關磁阻電機（簡稱SRM）的興趣。主要原因還是由于SRM具有結構簡單、成本低、運行可靠、低速轉矩大、簡單的功率轉換電路、控制方式靈活和效率高等優點。雖然SRM在過去的幾年里有了很大發展，但仍存在一些問題有待研究，如與一般電機相比其轉距脈動比較明顯，這就限制了其在伺服傳動系統中的應用。為了使SRM能在伺服領域中發揮其固有的優點，研究如何有效的抑制SRM低速轉矩脈動具有十分重要的意義。在這方面各國學者做了大量的研究，有人提出按在飽和運行時產生近似正弦的轉矩/轉角靜態特性來優化電動機的結構設計，并且采用伺服電動機控制器產生正弦的希望電流/轉角分布，以此削弱瞬時轉矩脈動。文獻[1]中采用模糊自適emerging SRM.應控制方案，模糊參數從開始的自由選擇到最后調整為最優。文獻[2]中采用局部逼近的神經網絡，對期望的電流波形進行在線學習，從而實現轉矩脈動的最小化。但上述方法并沒得到廣泛的實際應用，其原因主要是其控制方案復雜，難以實時控制。

本文中通過借鑒步進電機細分驅動技術，結合分析SRM矩角特性為本文的控制策略提供理論上的依據，并在實驗過程中驗證了控制策略的實效性，達到實驗的目的，有效地減小轉矩脈動，并使噪聲大大減小。

??? 二、微分驅動的原理

??? 在步進電機的驅動控制中，將電機繞組中的電流對應各個平衡位置進行細分，由常規的矩形波供電改成階梯波供電，繞組中的電流經過若干個階梯上升到額定值或者從額定值經過若干個階梯下降到零。經過細分后，驅動電流的變化幅度大大減小。故轉子到達平衡位置時的過剩能量也大為減少；另一方面，控制信號的頻率提高了N倍（細分數），故可遠離轉子的低頻諧振頻率。因此，運用細分驅動不僅能使電機運行平穩，而且還能減弱或消除振蕩引起的低頻噪聲。

從上述可以看出，步進電機的細分實質是在電機各相繞組的電流切換時代替原來的繞組電流直接通斷的方法。對于SRM而言，其工作原理與大角度步進電動機相似，定子磁動勢在空間以一個較大的步進角步進運行，由此我們考慮到在SRM驅動中是否也可以借鑒步進電機細分驅動的思想，在換相時細分繞組電流使通過繞組的電流階梯變化，通過控制各相電流的大小使繞組轉矩矢量在轉子的各平衡位置保持大小基本恒定，即減小了轉矩脈動。

三、SRM轉矩矢量控制原理

在SRM矩角特性分析中，若忽略磁路的非線性因素影響，電磁轉距可表示為：

式中L為SRM相繞組的直感，忽略高次諧波，相繞組自感為：

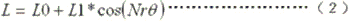
式中：L0、L1為自感的恒定分量和基波分量的幅值，可以認為是常數。Nr為SRM轉子齒數

由（1）、（2）可得：

T(θ,i)=-Tmax*sin(Nrθ)……………………（3）

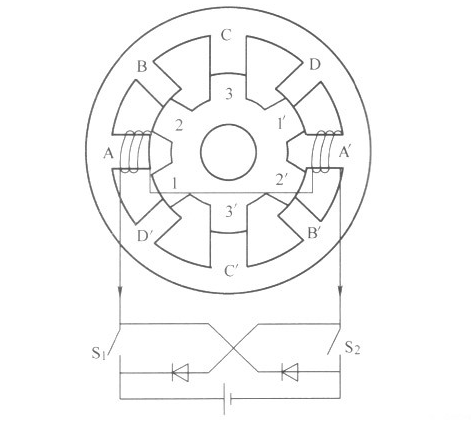
所以，每相繞組產生的基波電磁轉矩是一種空間正弦波，穩定零位取決于該相磁極中心線的位置。電磁轉矩是轉子位置θ和相電流的函數。因此，可以用空間矢量TA代表A相繞組的電磁轉矩，其相位和A相繞組磁極中心線一致。在開關磁阻電機步進運動分析中，旋轉磁場轉矩矢量圖可以使分析形象化，在本文的分析中以（8/6）四相SR電動機為例，如圖1。

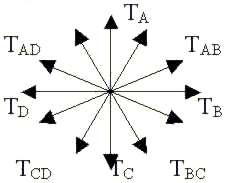
圖1 SRM旋轉磁場轉矩矢量

??? 對于（8／6）四相SR電動機而言，A相繞組產生的穩定零位和B相繞組產生的穩定零位錯開一個步進角，在空間按幾何角度15度，若用電角度表示90度。如規定轉子順時針方向旋轉為正轉，則只要按A-B-C-D的順序依次給各相繞組供電，開關磁阻電動機的轉子以步進角15度一步一步的正轉。假定忽略電動機的互感，允許將轉矩進行矢量相加，即得到圖1所示的旋轉磁場轉矩矢量，其中TAB 、TBC、TCA和TAD稱為派生轉矩矢量，表示兩相同時供電的合成轉矩；TA、TB、TC、TD稱為基本轉矩矢量，他們相位取決于定子磁極中心線的空間位置，表示一相單獨供電時的轉矩，相臨兩個轉矩錯開步進角3.75度。派生轉矩和基本轉矩的關系可表示為下列向量形式：

TAB=TA+TB…………………………（4）

??? 派生轉矩矢量的相位可以通過對繞組電流幅值的控制加以調節，使它出現在基本轉矩矢量之間的任何相位上，采用控制繞組電流的辦法增加SRM的每轉步數，提高分辨率，減小轉矩脈動。隨著電動機每轉細分步數的增加，可供選擇的最佳離散電流波形為正弦函數波形，如果能夠控制各相繞組的電流為正弦波，則實現SRM的連續控制。

四、微分驅動在SRM控制系統中的實現

由以上對(8/6)SRM轉矩控制原理的分析可知，開關磁阻電機細分驅動的核心就是為了實現轉矩矢量幅值相等，控制相繞組電流跟隨給定轉速對應的給定電流大小，使實時轉速保持在給定轉速誤差范圍內，從而有效減小了轉矩的脈動。

同時導通的兩相繞組電流可表示為下式，式中為合成矢量對應的電流大小：

ia=Im*cosθ；

ib=Im*sinθ； ………………………………………（5）

則合成電流矢量i（以ia為參考）：

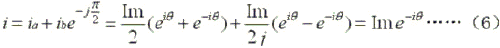
i是一個以Im為幅值，－θ為輻角的矢量。這樣，由式（1）、（6）可知，每當θ的值發生變化時，合成的矢量轉過一個相應的角度，且幅值大小保持不變，實現了恒力矩的細分驅動。利用式（5）可得到細分后通電相電流數據。

所以要控制轉矩必須控制電流，而控制電流是以控制PWM功率變換器輸出脈寬被調制的功率開關信號為直接控制量，使實際輸出電流按階梯波電流變化。因此SRM的微分驅動要靠控制PWM的占空比來實現。用下式表示加在導通相繞組的PWM信號的占空比：

??? Ya＝Y*cosθ ；

??? Yb＝Y*sinθ ；……………………………………（7）

??? 上式中：Y為占空比幅值； Ya，Yb分別為Y在通電相繞組的分量；θ為轉矩角；

??? （7）式中的占空比幅值Y與 速度閉環中的給定速度通過量化換算得出線性對應關系：

?? ?Y=k*n；k為比例系數；

??? 所以在速度給定的前提下，占空比幅值Y保持恒定，由（7）式可知，只要調整特定平衡位置的轉矩角即可控制各相PWM脈寬占空比分量，根據（5）式與（7）式的對應關系，由各相占空比分量大小的變化從而控制了導通相電流的大小。

（8/6）四相SRM轉子極距角（周期）為60度，每相步進角為15度，因此微分驅動的行為即是要細分該15度的步進角，在15度的步進角中找到三個轉矩平衡位置，由于SRM繞組電流的大小受PWM功率變換器控制，所以調節PWM輸出脈寬即可使實際輸出電流如圖2所示按階梯波電流變化，各相通電順序為：

電機正轉時：A-AB1-AB2-AB3-B-BC1-BC2-BC3-C-CD1-CD2-CD3-D-DA1-DA2-DA3-A

??? 反轉時：A-AD1-AD2-AD3-D-DC1-DC2-DC3-C-CB1-CB2-CB3-B-BA1-BA2-BA3-A

圖2（8/6）SRM細分繞組理想電流波形

在SRM轉子位置檢測中，由光電旋轉編碼器檢測轉子位置產生較高分辨率的數字信號。如轉子每旋轉一周（360度）能產生N個信號，則稱其為Np/r（脈沖/轉）。把N個脈沖信號細分，每轉過N/96個脈沖調整一次相繞組電流大小，使轉子的一個大步距角細分成4個小的步距角。從而使電流用換相區代替換相點，即在換相時關斷相電流不是立即關斷到零，而是按階梯下降；導通相也并不是立即導通，而是按階梯逐漸導通。階梯的寬度 即PWM脈寬占空比由32個脈沖轉過的時間決定。

控制系統原理如圖3所示，實際轉速與給定轉速相比較產生的偏差信號通過調節器經過PID運算產生給定轉速對應PWM脈寬占空比Y，同時根據轉子位置脈沖查表對應平衡位置轉矩角θ對應的正余弦值，經過算術運算求得實時通電相PWM占空比幅度Ya、Yb，即控制了通過SRM繞組的有效電流大小。

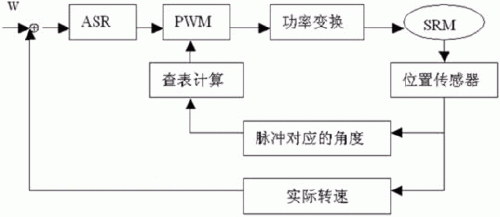
圖3 SRM細分驅動控制原理圖

五、實驗與結論

本文論述的微分驅動SRM的控制策略在具體實施階段，選用了Microchip公司的PIC18F2331高檔八位單片機，該芯片內部集成了豐富的外設資源，其中功率控制PWM模塊、CCP模塊、A/D模塊、光電編碼器接口（QEI）等為SRM的控制提供了方便。

利用CCP模塊的捕捉模式，當轉子位置信息脈沖符合設定的條件時（上升沿或下降沿出現），中斷標志位CCP1IF被硬件自動置位，產生一次CCP1捕捉中斷。將TMR1的計數值傳送到CCPR1寄存器。根據計數值可計算電機轉速。

在PIC18F2331中，功率控制PWM模塊支持三個PWM發生器和六個輸出通道。在本系統中，功率變換部分采用半橋式電路，相與相之間完全獨立，每相需要一個IGBT作為主開關器件，所以只要選用兩個PWM發生器和四個輸出通道即可滿足電機的驅動控制。

A/D模塊為10位高速轉換器，可通過寄存器設置芯片的工作電壓作為A/D轉換的參考電壓（即使用VCC為參考電壓）。則模擬信號的輸入范圍為0~VREF。

相電流采樣選用霍爾電流傳感器采樣電流信號，霍爾電流傳感器本身已存在濾波電路，輸出可直接提供給單片機的A/D模塊。

在本控制系統中采用了光電編碼器測量轉子位置，作為閉環控制的反饋量。PIC18F2331提供了這種編碼器的接口電路，編碼脈沖通過2個引腳QEA和INDX 輸入到芯片內部作為輸入時鐘，時鐘信號使位置計數器寄存器（POSCNT）遞增。此寄存器的工作模式決定了是在QEA 輸入沿遞增。如果與周期寄存器MAXCNT 匹配該寄存器復位。如果允許位置計數器中斷，當POSCNT復位時會產生一個中斷。

由于本系統采用了外設資源集成度比較高的PIC單片機，所以硬件電路比較簡單。 系統框圖如下：

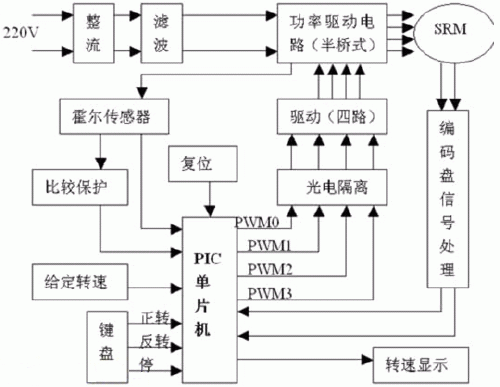
圖4 系統框圖

經過實驗驗證，該微分驅動控制方法使SRM最低可平穩運行在20r/min的轉速，在低速運行狀態下的轉矩脈動大大減小，轉動時的噪聲也得到了有效的改善。

　　但是如果在感性負載的情況下，電動機中電流的上升或衰減并不是瞬時完成的。尤其在SRM高速運行時，繞組中電流只有很短的時間來跟蹤給定，因此微步細分的步數和轉速都受到一定程度的限制，并不能無限微步細分。

參考文獻

[1] S. Mir, M.E. Elbuluk, I. Husain, Torque-ripple minimization in switched reluctance motors using adaptive fuzzy control, IEEE Trans. Industry Appl. 35 (2) (1999) 461_/468 (March/April).

??? [2] Reay D S , Green T C, Williams B W .Application of Associative Memory Neural Networks to the Control of a Switched Reluctance Motor[c].Proc.IECON’93,Maui,HI.

??? [3] 王宏華. 開關型磁阻電動機調速控制技術. 機械工業出版社, 1995.

??? [4] 王鴻鈺，步進電機控制技術入門，1990.

??? [5] PIC18F2331/2431/4331/4431數據手冊，Microchip Technology Inc.

??? [6] 劉和平等 PIC18FXXX單片機程序設計及應用，北京航空航天大學出版社，2005.