電路問題計算的先決條件是正確識別電路,搞清楚各部分之間的連接關(guān)系。對較復(fù)雜的電路應(yīng)先將原電路簡化為等效電路,以便分析和計算。
識別電路的方法很多,現(xiàn)結(jié)合具體實例介紹十種方法。
特征識別法
串并聯(lián)電路的特征是:串聯(lián)電路中電流不分叉,各點電勢逐次降低,并聯(lián)電路中電流分叉,各支路兩端分別是等電勢,兩端之間等電壓。根據(jù)串并聯(lián)電路的特征識別電路是簡化電路的一種最基本的方法。? 舉例:試畫出圖 1 所示的等效電路。
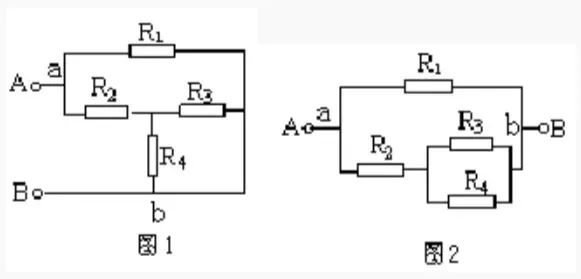
解:設(shè)電流由 A 端流入,在 a 點分叉,b 點匯合,由 B 端流出。支路 a—R1—b 和 a—R2—R3(R4)—b 各點電勢逐次降低,兩條支路的 a、b 兩點之間電壓相等,故知 R3 和 R4 并聯(lián)后與 R2 串聯(lián),再與 R1 并聯(lián),等效電路如圖 2 所示。 ? ? ? ?
伸縮翻轉(zhuǎn)法
在實驗室接電路時常常可以這樣操作,無阻導(dǎo)線可以延長或縮短,也可以翻過來轉(zhuǎn)過去,或?qū)⒁恢贩絼e處,翻轉(zhuǎn)時支路的兩端保持不動;導(dǎo)線也可以從其所在節(jié)點上沿其它導(dǎo)線滑動,但不能越過元件。這樣就提供了簡化電路的一種方法,我們把這種方法稱為伸縮翻轉(zhuǎn)法。? 舉例:畫出圖 3 的等效電路。
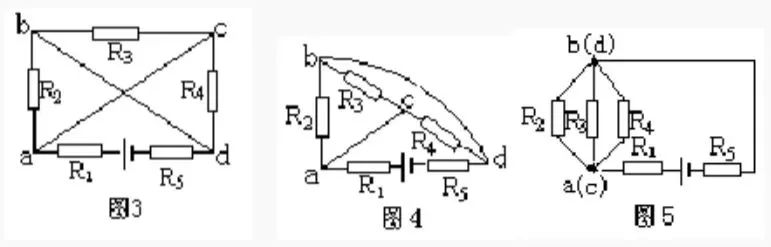
解:先將連接 a、c 節(jié)點的導(dǎo)線縮短,并把連接 b、d 節(jié)點的導(dǎo)線伸長翻轉(zhuǎn)到 R3—C—R4 支路外邊去,如圖 4。 ? 再把連接 a、c節(jié)點的導(dǎo)線縮成一點,把連接 b、d 節(jié)點的導(dǎo)線也縮成一點,并把 R5 連到節(jié)點 d 的導(dǎo)線伸長線上(圖 5)。由此可看出 R2、R3 與 R4 并聯(lián),再與 R1 和 R5 串聯(lián),接到電源上。 ? ? ? ?
電流走向法
電流是分析電路的核心。從電源正極出發(fā)(無源電路可假設(shè)電流由一端流入另一端流出)順著電流的走向,經(jīng)各電阻繞外電路巡行一周至電源的負極,凡是電流無分叉地依次流過的電阻均為串聯(lián),凡是電流有分叉地分別流過的電阻均為并聯(lián)。? 舉例:試畫出圖 6 所示的等效電路。
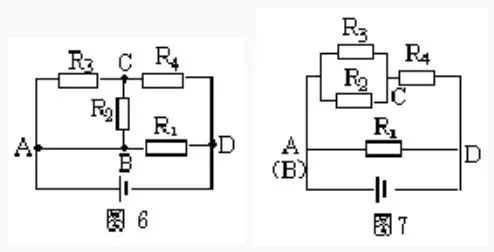
解:電流從電源正極流出過 A 點分為三路(AB 導(dǎo)線可縮為一點),經(jīng)外電路巡行一周,由 D 點流入電源負極。第一路經(jīng) R1 直達 D 點,第二路經(jīng) R2 到達 C 點,第三路經(jīng) R3 也到達 C 點,顯然 R2 和 R3 接聯(lián)在 AC 兩點之間為并聯(lián)。二、三路電流同匯于 c 點經(jīng) R4 到達 D 點,可知 R2、R3 并聯(lián)后與 R4 串聯(lián),再與 R1 并聯(lián),如圖 7 所示。 ? ? ? ?
等電勢法
在較復(fù)雜的電路中往往能找到電勢相等的點,把所有電勢相等的點歸結(jié)為一點,或畫在一條線段上。當兩等勢點之間有非電源元件時,可將之去掉不考慮;當某條支路既無電源又無電流時,可取消這一支路。我們將這種簡比電路的方法稱為等電勢法。? 舉例:如圖 8 所示,已知 R1 = R2 = R3 = R4 = 2Ω ,求 A、B 兩點間的總電阻。
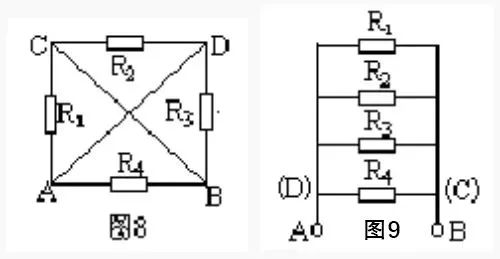
解:設(shè)想把 A、B 兩點分別接到電源的正負極上進行分析,A、D 兩點電勢相等,B、C 兩點電勢也相等,分別畫成兩條線段。電阻 R1 接在 A、C 兩點,也即接在 A、B 兩點;R2 接在 C、D 兩點,也即接在 B、A 兩點;R3 接在 D、B 兩點,也即接在 A、B 兩點,R4 也接在 A、B 兩點,可見四個電阻都接在 A、B 兩點之間均為并聯(lián)(圖 9)。所以,PAB=3Ω。 ? ? ? ?
支路節(jié)點法
節(jié)點就是電路中幾條支路的匯合點。所謂支路節(jié)點法就是將各節(jié)點編號(約定:電源正極為第 1 節(jié)點,從電源正極到負極,按先后次序經(jīng)過的節(jié)點分別為 1、2、3……),從第 1 節(jié)點開始的支路,向電源負極畫。可能有多條支路(規(guī)定:不同支路不能重復(fù)通過同一電阻)能達到電源負極,畫的原則是先畫節(jié)點數(shù)少的支路,再畫節(jié)點數(shù)多的支路。然后照此原則,畫出第 2 節(jié)點開始的支路。余次類推,最后將剩余的電阻按其兩端的位置補畫出來。? 舉例:畫出圖 10 所示的等效電路。
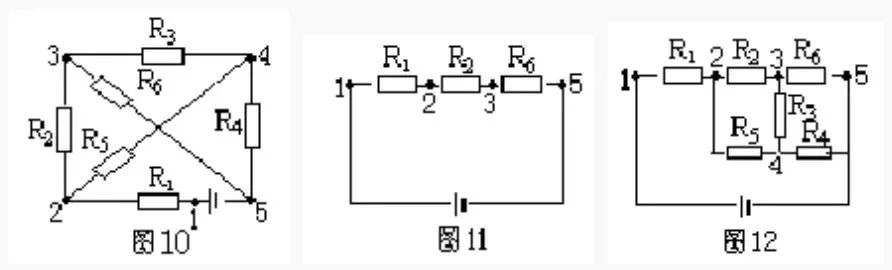
解:圖 10 中有 1、2、3、4、5 五個節(jié)點,按照支路節(jié)點法原則,從電源正極(第 1 節(jié)點)出來,節(jié)點數(shù)少的支路有兩條:R1、R2、R5 支路和 R1、R5、R4 支路。取其中一條 R1、R2、R5 支路,畫出如圖 11。 ? 再由第 2 節(jié)點開始,有兩條支路可達負極,一條是 R5、R4,節(jié)點數(shù)是 3,另一條是 R5、R3、R5,節(jié)點數(shù)是 4,且已有 R6 重復(fù)不可取。所以應(yīng)再畫出 R5、R4 支路,最后把剩余電阻 R3 畫出,如圖 12 所示。 ? ? ? ?
幾何變形法
幾何變形法就是根據(jù)電路中的導(dǎo)線可以任意伸長、縮短、旋轉(zhuǎn)或平移等特點,將給定的電路進行幾何變形,進一步確定電路元件的連接關(guān)系,畫出等效電路圖。? 舉例:畫出圖 13 的等效電路。
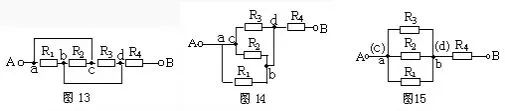
解:使 ac 支路的導(dǎo)線縮短,電路進行幾何變形可得圖 14,再使 ac 縮為一點,bd 也縮為一點,明顯地看出 R1、R2 和 R5 三者為并聯(lián),再與 R4 串聯(lián)(圖 15)。 ? ? ? ?
撤去電阻法
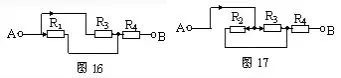
根據(jù)串并聯(lián)電路特點知,在串聯(lián)電路中,撤去任何一個電阻,其它電阻無電流通過,則這些電阻是串聯(lián)連接;在并聯(lián)電路中,撤去任何一個電阻,其它電阻仍有電流通過,則這些電阻是并聯(lián)連接。? 舉例:仍以圖 13 為例,設(shè)電流由 A 端流入,B 端流出,先撤去 R2,由圖 16 可知 R1、R3 有電流通過。再撤去電阻 R1,由圖 17 可知 R2、R3 仍有電流通過。同理撤去電阻 R3 時,R1、R2 也有電流通過由并聯(lián)電路的特點可知,R1、R2 和 R3 并聯(lián),再與 R4 串聯(lián)。
獨立支路法
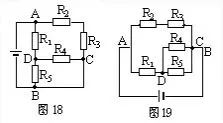
讓電流從電源正極流出,在不重復(fù)經(jīng)過同一元件的原則下,看其中有幾條路流回電源的負極,則有幾條獨立支路。未包含在獨立支路內(nèi)的剩余電阻按其兩端的位置補上。應(yīng)用這種方法時,選取獨立支路要將導(dǎo)線包含進去。? 舉例:畫出圖 18 的等效電路。
?
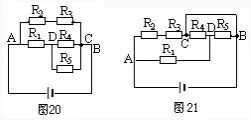
方案一:選取 A—R2—R3—C—B 為一條獨立支路,A—R1—R5—B 為另一條獨立支路,剩余電阻 R4 接在 D、C 之間,如圖 19 所示。
方案二:選取 A—R1—D—R4—C—B 為一條獨立支路,再分別安排 R2、R3 和 R5,的位置,構(gòu)成等效電路圖 20。
方案三:選取 A—R2—R3—C—R4—D—R5—B 為一條獨立支路,再把 R1 接到 AD 之間,導(dǎo)線接在 C、B 之間,如圖 21 所示,結(jié)果仍無法直觀判斷電阻的串并聯(lián)關(guān)系,所以選取獨立支路時一定要將無阻導(dǎo)線包含進去。
節(jié)點跨接法
將已知電路中各節(jié)點編號,按電勢由高到低的順序依次用 1、2、3……數(shù)碼標出來(接于電源正極的節(jié)點電勢最高,接于電源負極的節(jié)點電勢最低,等電勢的節(jié)點用同一數(shù)碼,并合并為一點)。然后按電勢的高低將各節(jié)點重新排布,再將各元件跨接到相對應(yīng)的兩節(jié)點之間,即可畫出等效電路。? 舉例:畫出圖 22 所示的等效電路。
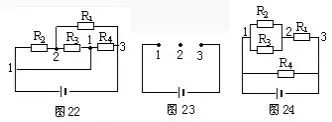
解:節(jié)點編號如圖 22 中所示。節(jié)點排列,將 1、23 節(jié)點依次間隔地排列在一條直線上,如圖 23。元件歸位,對照圖 22,將 R1、R2、R3、R4 分別跨接在排列好的 1、2 的等效電路如圖 24。 ? ? ? ?
電表摘補法
若復(fù)雜的電路接有電表,在不計電流表 A 和電壓表 V 的內(nèi)阻影響時,由于電流表內(nèi)阻為零,可摘去用一根無阻導(dǎo)線代替;由于電壓表內(nèi)阻極大,可摘去視為開路。用上述方法畫出等效電 搞清連接關(guān)系后,再把電表補到電路對應(yīng)的位置上。? 舉例:如圖 25 的電路中,電表內(nèi)阻的影響忽略不計,試畫出它的等效電路。
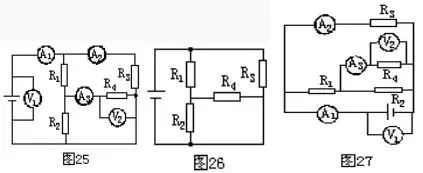
解:先將電流去,用一根導(dǎo)線代摘替,再摘去電壓表視為開路,得圖 26。然后根據(jù)圖 25 把電流表和電壓表補接到電路中的對應(yīng)位置上,如圖 27 所示。
審核編輯:湯梓紅
 電子發(fā)燒友App
電子發(fā)燒友App






















評論