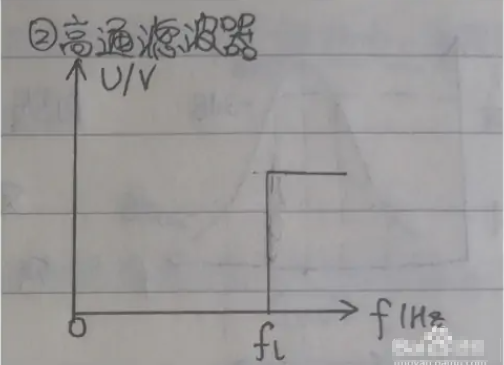
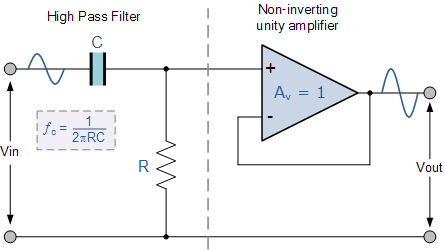
高通濾波器是一種讓某一頻率以上的信號分量通過,而對該頻率以下的信號分量大大抑制的電容、電感與電阻等器件的組合裝置。其特性在時域及頻域中可分別用沖激響應及頻率響應描述。后者是用以頻率為自變量的函數表示,一般情況下它是一個以復變量jω為自變量的的復變函數,以H(jω)表示。它的模H(ω)和幅角φ(ω)為角頻率ω的函數,分別稱為系統的“幅頻響應”和“相頻響應”,它分別代表激勵源中不同頻率的信號成分通過該系統時所遇到的幅度變化和相位變化。可以證明,系統的“頻率響應”就是該系統“沖激響應”的傅里葉變換。當線性無源系統可以用一個N階線性微分方程表示時,頻率響應H(jω)為一個有理分式,它的分子和分母分別與微分方程的右邊和左邊相對應。
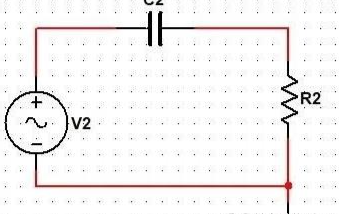
電容和電阻組成的高通濾波器
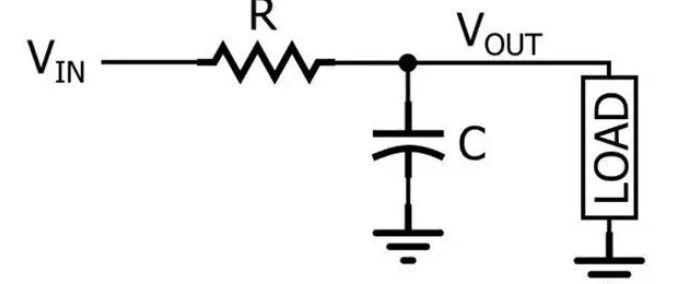
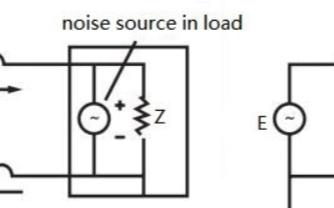
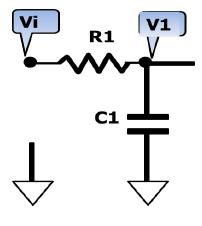
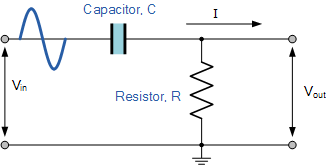
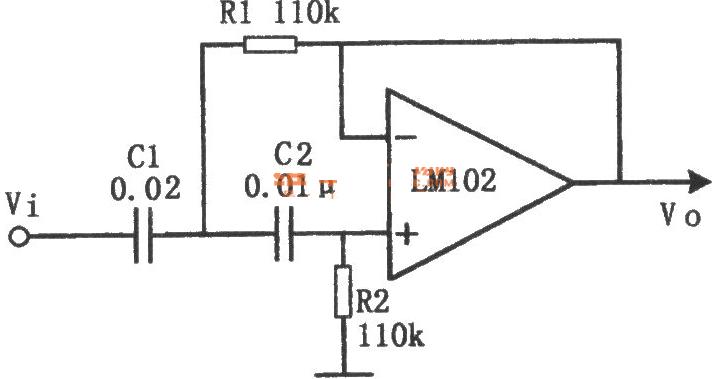
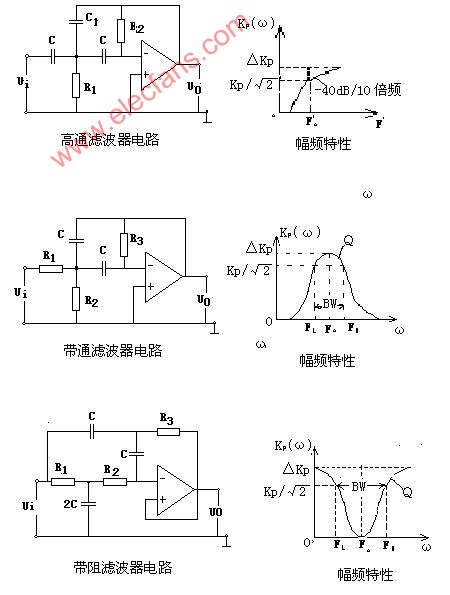
電阻和電容組成的高通濾波器的電路如下:
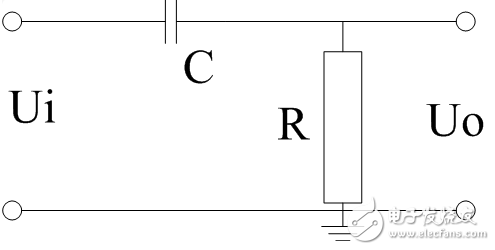
電阻的阻抗是固定值,為R。
電容的容抗與信號頻率f有關,Xc=1/2πfC。
輸出電壓Uo=Ui*R/(R-jXc)
|Uo|
=Ui*R/√(R^2+Xc^2)
=Ui*R/√(R^2+1/(2πfC)^2)
=Ui/√(1+1/(2πfRC)^2)
記1/2πRC為f0,f0為濾波器的截止頻率。
那么,
|Uo|=Ui/√(1+(f0/f)^2)
f=f0時,|Uo|=√2/2*Ui
f趨向0時,|Uo|趨向Ui
f趨向無窮大時,|Uo|趨向0。
f越大,|Uo|越小。
高通濾波器原理解析
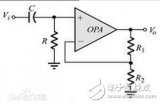
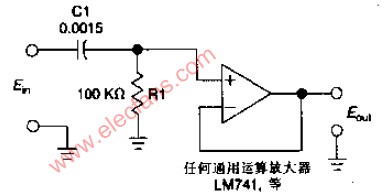
最簡單的高通濾波器是“一階高通濾波器”,它的的特性一般用一階線性微分方程表示,它的左邊與一階低通濾波器完全相同,僅右邊是激勵源的導數而不是激勵源本身。當較低的頻率通過該系統時,沒有或幾乎沒有什么輸出,而當較高的頻率通過該系統時,將會受到較小的衰減。實際上,對于極高的頻率而言,電容器相當于“短路”一樣,這些頻率,基本上都可以在電阻兩端獲得輸出。換言之,這個系統適宜于通過高頻率而對低頻率有較大的阻礙作用,是一個最簡單的“高通濾波器”。
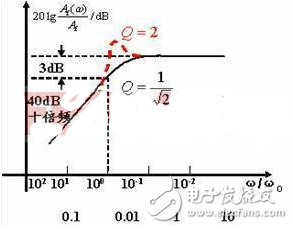
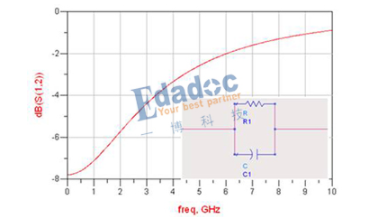
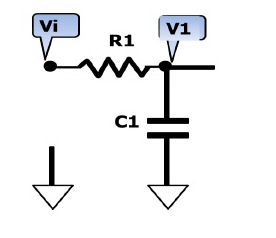
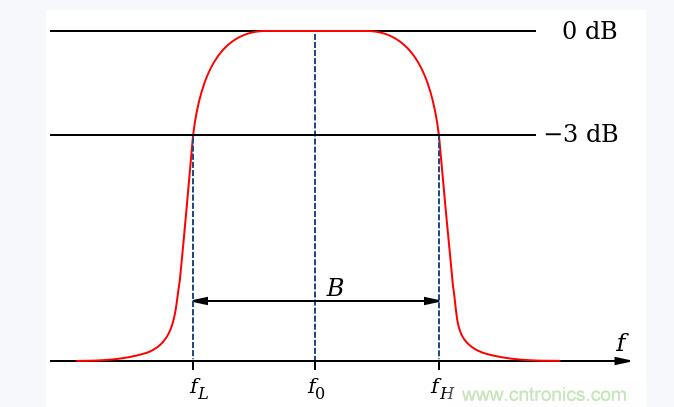
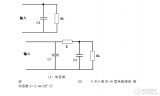
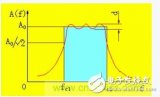
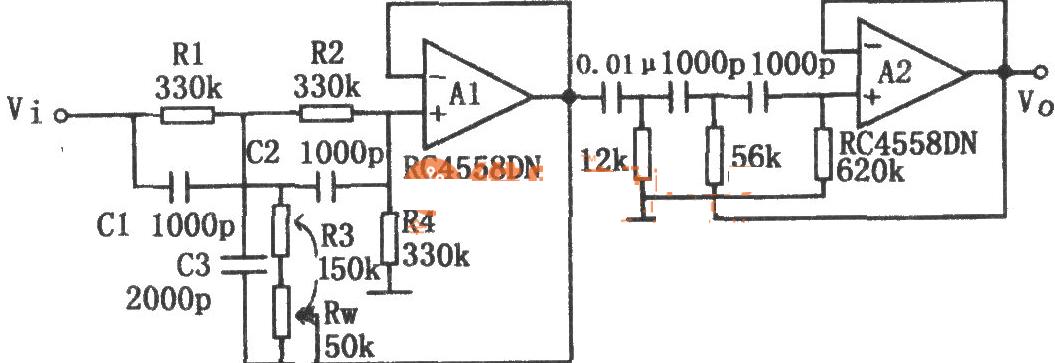
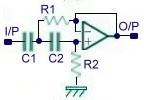
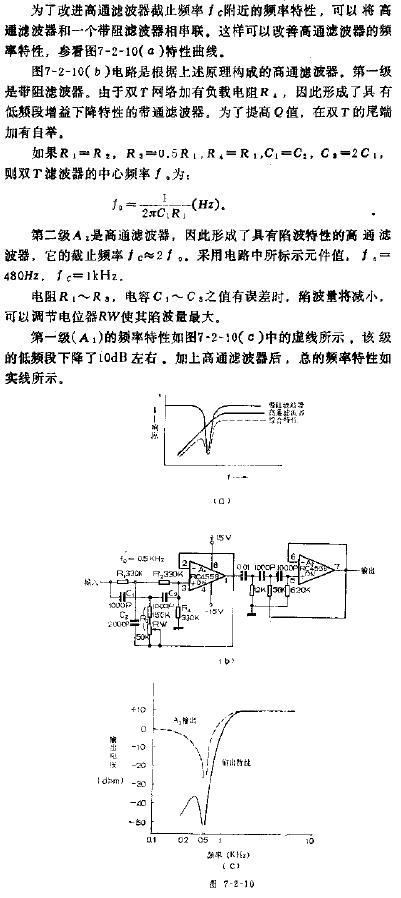
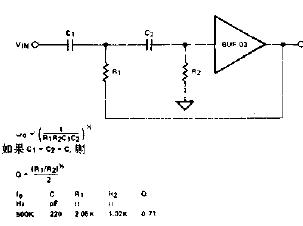
下圖是RC元件構成的高通濾波器。圖(a)是電路, 圖(b)是這一高通濾波器的幅頻特性曲線。從這一曲線可以看出,當輸入信號Vi中頻率低干轉折頻率f。時,輸出受到明顯的衰減。高于轉折頻率f。的信號輸出大。
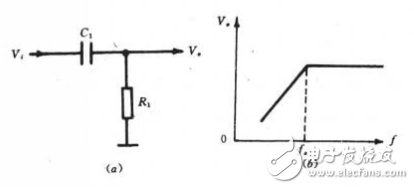
這一電路的工作原理是這樣:當頻率低于f。的信號輸入這一濾波器時,由于C1的容抗很大而受到阻止,輸出減小,且頻率愈低輸出愈小。當頻率高于f。的信號輸入這一濾波器時,由于C1容抗已很小,故對信號無衰減作用,這樣該濾波器具有讓高頻信號通過,阻止低頻信號的作用。這一電路的轉折頻率f。由下式決定:
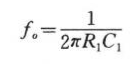
 電子發燒友App
電子發燒友App











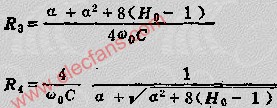
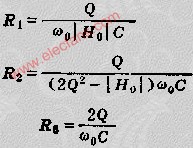
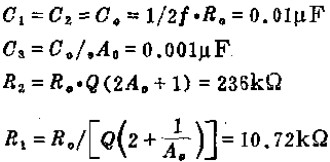












評論