1.2 數制和碼制
1 . 2 . 1 數 制
一、十進制
二、二進制
三、八進制和十六進制
1 .2 .2 不同數制間的轉換
一、各種數制轉換成十進制
二、十進制轉換為二進制
三、二進制與八進制、十六進制間相互轉換
1 .2 .3 二進制代碼
一、二-十進制代碼
8421碼、5421碼和余3碼
二、可靠性代碼
1．格雷碼
2．奇偶校驗碼
作業：P10 2.（1）（3）3.（1）（3）4. （4）5. （4）6. （4）
7.（4）
第1章 緒 論

1.1 概述
1 . 1 . 1 數字信號和數字電路
電信號 — 隨時間變化的電流或電壓。
1、數字信號與模似信號
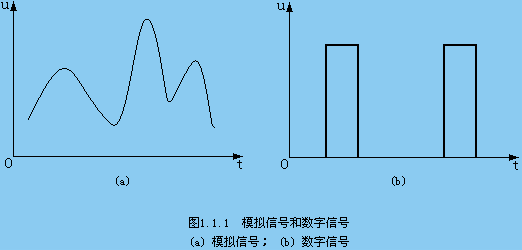
模擬信號 — 幅度隨時間連續變化
數字信號 — 斷續變化（離散變化），時間上離散幅值上整量化，多采用0、1二種數值組成又稱二進制信號。
舉例P1圖1.1.1。與同學討論離散信號。

2、模擬電路與數字電路
模擬電路 — 傳輸或處理模擬信號的電路，如：電壓、功率放大等；
數字電路 — 處理、傳輸、存儲、控制、加工、算運算、邏輯運算、數字信號的電路。
如測電機轉速：電機-光電轉換-整形-門控-計數器-譯碼器-顯示
時基電路
1 . 1 . 2 數字電路的分類
微電子技術的迅猛發展導致了數字電路的飛速發展。
1、 按電路類型分類
（1）組合邏輯電路 輸出只與當時的輸入有關，如：編碼器、加減法器、比較器、數據選擇器。
（2）時序邏輯電路 輸出不僅與當時的輸入有關，還與電路原來的狀態有關。
如：觸發器、計數器、寄存器
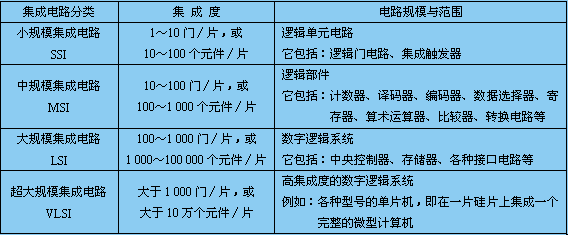
2、 按集成度分類
SSI →MSI→LIS→VLSI

?表1.1.1 數字集成電路分類

3、 按半導體的導電類型分類
（1） 雙極型電路
（2） 單極型電路

1 . 1 . 3 數字電路的優點
1、 易集成化。 兩個狀態“0”和“1”，對元件精度要求低。
2、 抗干擾能力強，可靠性高。 信號易辨別不易受噪聲干擾。
3、便于長期存貯。 軟盤、硬盤、光盤。
4、通用性強，成本低，系列多。
（國際標準）TTL系例數字電路、門陣列、可編程邏輯器件。
5、保密性好。 容易進行加密處理。

1 . 1 . 4 脈沖波形的主要參數
在數字電路中，加工和處理的都是脈沖波形，而應用最多的是矩形脈沖。
圖1 . 1 . 2 脈沖波形的參數

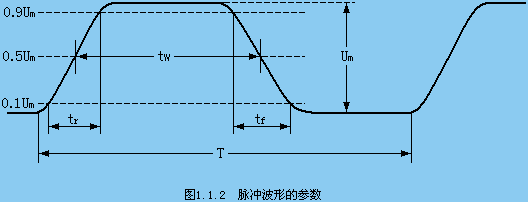
1．脈沖幅度 。 脈沖電壓波形變化的最大值，單位為伏（V）。
2．脈沖上升時間。 脈沖波形從0.1Um上升到0.9Um所需的時間。
3．脈沖下降時間 。脈沖波形從0.9Um下降到0.1Um所需的時間。
脈沖上升時間tr 和下降時間tf 越短，越接近于理想的短形脈沖。單位為秒（s）、毫秒（ms）、微秒（ us）、納秒（ns）。
4．脈沖寬度 。 脈沖上升沿0.5Um 到下降沿0.5Um 所需的時間，單位和 tr、tf 相同。

5．脈沖周期T。 在周期性脈沖中，相鄰兩個脈沖波形重復出現所需的時間，單位和tr 、tf 相同。
6．脈沖頻率f：每秒時間內，脈沖出現的次數。 單位為赫茲（Hz）、千赫茲（kHz）、兆赫茲（MHz），f ＝1∕T。
7．占空比q：脈沖寬度 與脈沖重復周期T的比值。q ＝ ∕T。
它是描述脈沖波形疏密的參數。

1.2 數制和碼制
1 . 2 . 1數 制
一、十進制
1、表示法


與同學討論二、八、十六進制的表示方法及特點

二、二進制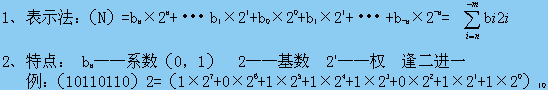

三、八進制和十六進制
1．八進制
逢八進一；系數0～7 ；基數8； 權8 n。
2．十六進制
逢十六進一；系數：0～9、A、B、C、D、E、F；基數16；權16n。

表1.2.1 十進制、二進制、八進制、十六進制對照表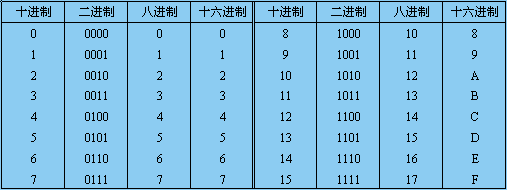
　

1 . 2 . 2 不同數制間的轉換
一、各種數制轉換成十進制
二進制、八進制、十六進制轉換成十進制時，只要將它們按權展開，求出各加權系數的和，便得到相應進制數對應的十進制數。
例：

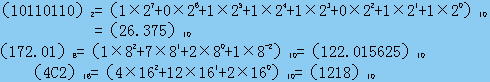
二、十進制轉換為二進制
將十進制數的整數部分轉換為二進制數采用“除2取余法”；
將十進制小數部分轉換為二進制數采用“乘2取整法”。
例1.1.1將十進制數(107.625)10轉換成二進制數。
將十進制數的整數部分轉換為二進制數采用“除2取余法”，它是將整數部分逐次被2除，依次記下余數，直到商為0。第一個余數為二進制數的最低位，最后一個余數為最高位。
解：① 整數部分轉換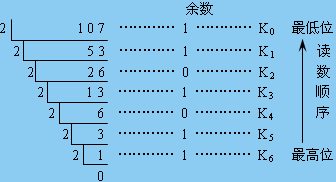


所以，
②小數部分轉換
將十進制小數部分轉換為二進制數采用“乘2取整法”，它是將小數部分連續乘以2，取乘數的整數部分作為二進制數的小數。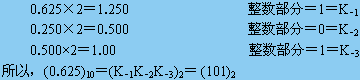
由此可得十進制數(107.625)10對應的二進制數為
(107.625)10＝(1101011.101)2

三、二進制與八進制、十六進制間相互轉換
1．二進制和八進制間的相互轉換
（1） 二進制數轉換成八進制數。
二進制數轉換為八進制數的方法是：整數部分從低位開始，每三位二進制數為一組，最后不足三位的，則在高位加0補足三位為止；小數點后的二進制數則從高位開始，每三位二進制數為一組，最后不足三位的，則在低位加0補足三位，然后用對應的八進制數來代替，再按順序排列寫出對應的八進制數。
例1.1.2 將二進制數(11100101.11101011)2轉換成八進制數。
(11100101.11101011)2＝(345.726)8

（2） 八進制數轉換成二進制數。
將每位八進制數用三位二進制數來代替，再按原來的順序排列起來，便得到了相應的二進制數。
例1.1.3 將八進制數(745.361)8轉換成二進制數。
(745.361)8＝ (111100101.011110001)2

2．二進制和十六進制間的相互轉換
（1） 二進制數轉換成十六進制數。
二進制數轉換為十六進制數的方法是：整數部分從低位開始，每四位二進制數為一組，最后不足四位的，則在高位加0補足四位為止；小數部分從高位開始，每四位二進制數為一組，最后不足四位的，在低位加0補足四位，然后用對應的十六進制數來代替，再按順序寫出對應的十六進制數。
例1.1.4 將二進制數(10011111011.111011)2轉換成十六進制數。
(10011111011.111011)2＝(4FB.EC)16

（2）十六進制數轉換成二進制數。
將每位十六進制數用四位二進制數來代替，再按原來的順序排列起來便得到了相應的二進制數。
例1.1.5 將十六進制數(3BE5.97D)16轉換成二進制數。
(3BE5.97D)16＝(11101111100101.100101111101)2

1.2.3 二進制代碼
討論：碼的作用；BCD碼。
一、二-十進制代碼
將十進制數的0～9十個數字用二進制數表示的代碼，稱為二-十進制碼，又稱BCD碼。

表1.2.2 常用二-十進制代碼表（重點講解8421碼、5421碼和余3碼）

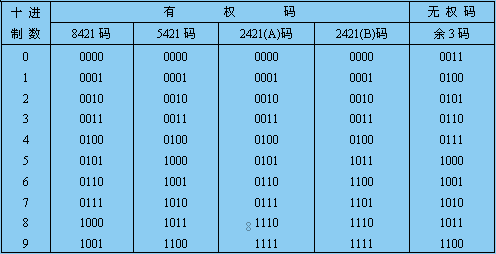
注意：含權碼的意義。

二、可靠性代碼
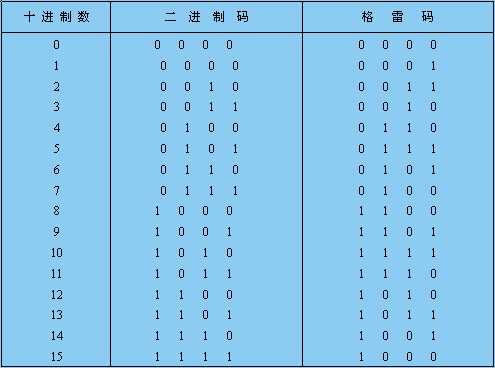
1．格雷碼

表1.2.3 格雷碼與二進制碼關系對照表

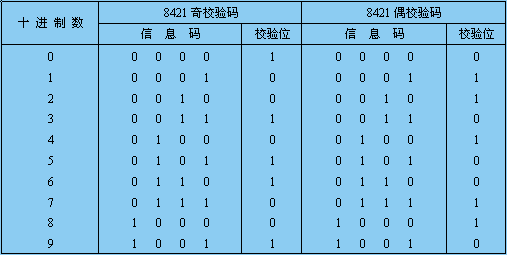
2．奇偶校驗碼
為了能發現和校正錯誤，提高設備的抗干擾能力，就需采用可靠性代碼，而奇偶校驗碼就具有校驗這種差錯的能力，它由兩部分組成。

表1.2.4 8421奇偶校驗碼