單通道的數據采集
2015-09-06 14:08:03
一種高性能、低價位的數據采集和開關主機安捷倫Agilent34970A是一種高性能、低價位的數據采集和開關主機,十分適于數據記錄、數據采集和一般的開關與控制應用。特性簡介:它是一種半機架寬的主機
2023-09-05 11:49:18
數據采集網關怎么采集數據?(數據采集流程)
2023-01-12 09:35:03 532
532 物通博聯全新推出的WG593工業數據采集網關能夠適用不同工業環境,在整個物聯網的系統之中遠程數據采集網關能顧發揮很大用處,物聯網遠程數據采集網關能過借助成熟的物聯網體系,遠程采集工業設備的PLC及其
2022-01-19 15:36:40 1064
1064 KEYSIGHT是德34901A數據采集模塊/20通道多路轉換器 是德34901A數據采集模塊適用于34970A和34972A數據采集儀,34901A特性 20 通道
2023-09-02 16:22:22
比較搞笑的 NI 員工出演的 數據采集廣告 Rap
2018-06-22 14:21:00 3860
3860 數據采集LABVIEW,有需要的朋友下來看看。
2016-01-20 16:26:39 551
551 數據采集應用案例,有需要的可以下來看看 。
2016-01-20 16:26:34 16
16 介紹了基于聲卡的數據采集系統的制作要點,運用labview開發系統,在普通配備聲卡的計算機上,實現了單通道數據采集。
2008-08-06 22:14:07 142
142
什么是數據采集?
2009-06-22 18:41:10 10074
10074 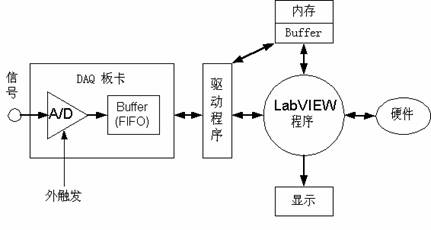
隨著工業自動化和智能制造的發展,數據采集和處理變得越來越重要。PLC數據采集和工業網關是工業自動化中的重要組成部分,數據采集工業網關作為連接不同設備的關鍵設備,承擔著數據采集、存儲、處理、分析和傳輸
2023-04-28 13:45:06 485
485 
基于STM32的數據采集模塊的設計及應用
2017-09-28 11:17:27 20
20 新的基于ARM的數據采集系統設計
2017-10-31 10:26:59 7
7 隨著人工智能技術的快速發展,數據采集和標注已成為人工智能領域中不可或缺的一部分。數據采集是獲取高質量數據的第一步,而數據標注則是保證數據質量的關鍵環節。在這篇文章中,我們將深入探討AI數據采集標注
2023-05-16 18:04:29 1266
1266 數據采集傳輸對于后續企業進行分析和決策是十分重要的,而實時數據采集更能提升整體生產的認識度,從而采取到更加及時高效的措施。因此PLC實時數據采集成為企業的基礎應用,那么如何實現PLC的實時數據采集呢?
2022-11-24 11:09:38 1127
1127 數據采集又稱數據收集,是一種從系統外部采集數據并輸入系統內部的接口。數據采集技術廣泛應用于各個領域。數據采集是指從傳感器等待測設備中自動采集信息的過程。數據采集系統是基于計算機的測量軟硬件產品,實現靈活、用戶定制的測量系統。
2022-11-08 11:11:12 3031
3031 數據采集又稱數據收集,是一種從系統外部采集數據并輸入系統內部的接口。數據采集技術廣泛應用于各個領域。數據采集是指從傳感器等待測設備中自動采集信息的過程。數據采集系統是基于計算機的測量軟硬件產品,實現靈活、用戶定制的測量系統。
2021-07-09 09:24:57 5648
5648 數據采集選型指南:數據采集,是指從傳感器和其它待測設備等模擬和數字被測單元中自動采集或產生信息的過程。數據采集系統采用基于計算機的測量軟硬件產品,實現靈活的、用
2009-09-06 22:50:56 29
29 分析了GPRS 技術在遠程數據采集中的應用現狀,針對實時數據采集傳輸的需要,設計和實現了基于GPRS 網絡的遠程數據采集傳輸系統。該系統利用GPRS 的Internet 接入功能,使用RS-232
2009-12-31 12:03:38 104
104 工業4.0的大潮中,很多應用都是由上位機、云來實現,那么PLC數據采集是最基本的前提條件之一。PLC數據采集如何實現?目前主流的PLC數據采集方式是通過工業網關來實現,工業網關具有強大的數據采集能力
2022-08-10 16:07:47 1018
1018 
基于LabVIEW的數據采集系統設計參考下。
2016-01-20 16:05:11 124
124 數據采集傳輸對于后續企業進行分析和決策是十分重要的,而實時數據采集更能提升整體生產的認識度,從而采取到更加及時高效的措施。因此PLC實時數據采集成為企業的基礎應用,那么PLC如何實現的實時數據采集呢?
2022-12-08 10:31:29 793
793 本文詳細介紹了一種基于 PCI 總線的高速數據采集系統的原理、組成和功能以及在 Windows 2000 環境下進行數據采集和存儲的方法。該系統用于某型號衛星下行的高速數據采集。系統設計與技術的通用性可應用于其它類似的高速數據采集與處理系統中。
2021-04-14 14:29:30 13
13 基于計算機技術及虛擬儀器平臺LabWindows/CVI 開發了多通道實時數據采集系統。系統采用ACL-8112PG 數據采集卡作為數據采集硬件,與單通道數據采集相比,多通道數據采集需要解決
2009-12-31 15:10:06 79
79 常見問題數據采集控制系統的組成? 1、變送器和執行器 2、信號調理器3、數據采集控制硬件4、計算機軟件
選擇數據采集卡要從那幾個方面進行考慮?
2008-08-03 20:28:05 41
41 數據采集應用案例,感興趣的可以瞧一瞧。
2016-12-19 16:59:52 2
2 ,沒有任何風險和損失!
我司研發銷售6軸、9軸電子羅盤(陀螺儀|加速計|磁力計)、傾角傳感器、姿態傳感器,慣導、數據采集盒、IoT遠程智慧監測等
產品廣泛應用
2021-10-29 15:28:31
本文主要介紹了matlab串口數據采集,matlab功能強大,串口操作也很簡單,通過以下幾個實例你就能掌握串口數據采集是怎么采集的。有需要的小伙伴可以看看。
2018-01-15 10:23:31 23708
23708 
數據采集方面入門級學習資料,比較全面系統介紹數據采集方面的原理及構成
2016-11-05 09:59:20 4
4 在本集中將給大家介紹數據采集技術的基本知識點,即完整的數據采集系統的組成部分,NI所能提供的數據采集硬件產品及適用領域,設備硬件選型過程中的重要參數等。幫您邁出數據采集的第一步。
2018-06-25 00:17:00 4999
4999 車載數據采集資料套件
有大量與車載數據采集資料下載
2010-03-26 12:13:59 19
19 關鍵詞:數據采集系統 , 脈沖信號采集 , 數據分析 1、 數據采集的必要性和歷史背景 數據采集的必要性和歷史背景.png 2、 納米軟件數據采集分析系統 數據采集分析系統可視化是使用可視化大屏
2020-03-24 10:01:30 965
965 TS511系列采集終端是集數據采集與2G/3G/4G/5G數據傳輸功能于一體的環保數據采集終端,完全符合《污染物在線自動監控(監測)系統數據傳輸標準》(HJ 212-2017) 和(HJ
2021-10-29 14:59:30
Python網絡數據采集教材免費下載。
2021-06-01 14:47:24 10
10 本文設計的高速數據采集系統是應用于芯片現場測試的實時數據采集系統,該數據采集系統的數據采集率是2 Gbps。
2012-04-19 10:05:11 1478
1478 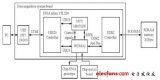
無線數據采集模塊設計,有需要的下來看看。
2016-08-19 17:04:53 19
19 基于FPGA的數據采集及顯示,下來看看。
2016-05-10 17:46:07 27
27 基于LabVIEW數據采集系統,有需要的下來看看。
2016-01-20 16:27:05 149
149 WD140系列工業數傳終端是一款工業級Modbus I/O數據采集及LORA傳輸智能終端,支持4G無線傳輸/LORA無線傳輸可選、支持IO數據采集、支持Modbus RTU協議和無線485透傳等功能
2022-08-06 15:08:24
什么是數據采集儀?它有什么作用? 數據采集儀是一種能夠采集環境、設備或物品數據的設備或系統。數據采集儀通常包含傳感器、數據存儲設備和數據處理軟件等組成部分。它的主要作用是收集和記錄環境和設備的數據
2023-08-11 09:27:09 284
284 
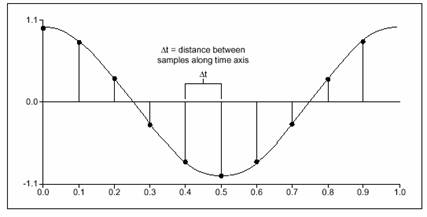
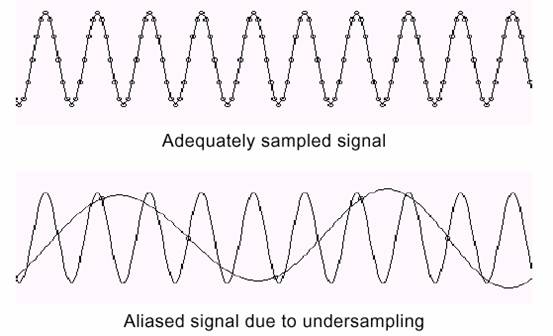 圖 2 不同采樣率的采樣結果
圖 2 不同采樣率的采樣結果 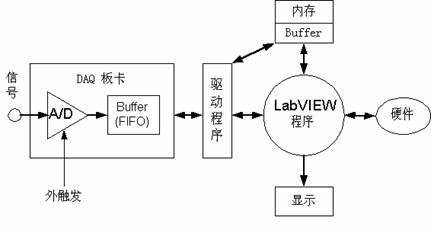
 電子發燒友App
電子發燒友App





























評論