傅里葉變換與拉普拉斯變換的聯系解讀 傅里葉變換和拉普拉斯變換都是數學中非常重要的分析工具。它們都在不同的領域中發揮著重要作用。 傅里葉變換是一種將時間域信號轉換成頻率域信號的技術。它是通過將信號
2023-09-07 17:04:19 219
219 Fourier Transform,簡稱DFT)則是適用于離散信號的傅里葉變換方法。 傅里葉變換的基本原理是將一個連續的信號,分解成一系列簡單的正弦波或者余弦波。而這些正弦波和余弦波,都有一個共同的周期,因此可以通過求取它們的頻率來描述一個信號。 離散傅里葉變換,則是將信號視
2023-09-07 17:04:15 330
330 分析、信號壓縮、特征提取等領域都有廣泛應用,本文將詳細介紹它們的差別和優缺點。 一、基本概念 1、傅里葉變換 傅里葉變換(Fourier transform,FT)是將時域信號轉換到頻域的一種數學變換,它可以分解一個信號成為若干個正弦、余弦波的疊加。傅里葉變換可以表示一個連續周期信號的頻率分量,但無法
2023-09-07 17:04:12 341
341 如何由傅里葉變換推出傅里葉反變換? 傅里葉變換和傅里葉反變換是信號處理和通信領域中的兩個重要概念,是數字信號和連續信號的重要數學分析方法之一。傅里葉變換可以將時間域信號轉化為頻率域信號,而傅里葉反
2023-09-07 17:04:09 356
356 小波變換與傅里葉變換的區別和聯系? 1. 傅里葉變換和小波變換的定義 傅里葉變換(Fourier Transform,簡稱FT)是一種將信號在時域上的函數轉變為頻域上的函數的方法,對于連續時間信號
2023-09-07 17:04:07 332
332 為什么有四種形式的傅里葉變換? 傅里葉變換是一種十分重要的數學工具,它可以將函數從時域(即時間域)轉換到頻域,從而能夠幫助人們更好地理解信號的特性。在傅里葉變換的研究過程中,出現了幾種不同的變形方式
2023-09-07 17:04:04 189
189 傅里葉變換重要公式總結 傅里葉變換公式常用公式 傅里葉變換是一種重要的數學工具,它可以將任意周期函數分解成一系列正弦函數或余弦函數的疊加形式。這些正弦函數和余弦函數被稱為頻率分量,它們的幅度和相位
2023-09-07 16:53:08 3859
3859 傅里葉變換公式理解 傅里葉變換是一種在數學、物理、工程和其他科學領域中常用的工具,它是一種將一個函數從時域轉換到頻域的方法。傅里葉變換可以將一個復雜的函數表示成一個頻域上各種周期函數的疊加,從而
2023-09-07 16:53:06 534
534 傅里葉變換和反變換公式? 傅里葉變換和反變換在信號處理領域中被廣泛應用。傅里葉變換是將一個時域信號轉換為頻域信號的過程,而傅里葉反變換則是將一個頻域信號轉換為時域信號的過程。這篇文章將詳細講解
2023-09-07 16:53:04 2916
2916 cos的傅里葉變換公式 ; 介紹 在數學中,傅立葉級數和傅立葉變換是分析周期函數和信號的兩種最重要的工具。傅立葉級數用于周期函數,而傅立葉變換用于非周期函數。在本文中,我們將重點討論余弦函數(cos
2023-09-07 16:53:02 860
860 傅里葉變換的實現方法? 傅里葉變換是一種將信號在時間域和頻率域之間相互轉換的數學工具。它的實現方法有很多種,其中最常見的是離散傅里葉變換(DFT)和快速傅里葉變換(FFT)。 離散傅里葉變換是一種將
2023-09-07 16:47:52 173
173 傅里葉變換公式總結? 傅里葉變換是一種將時域信號轉換為頻域信號的數學方法。它是通過將一個連續或離散的時域信號分解成一系列相位和幅度不同的正弦和余弦波形式,然后將它們表示到頻域中,以獲得更多的信息
2023-09-07 16:47:46 1222
1222 傅里葉變換和傅里葉逆變換的關系? 傅里葉變換和傅里葉逆變換是信號處理領域中極具重要性的數學工具,它們被廣泛應用于很多領域,例如音頻、圖像處理、通信等。 傅里葉變換是將一個信號在時域(即時間或空間)上
2023-09-07 16:43:47 581
581 傅里葉變換拉普拉斯變換和z變換的區別聯系 傅里葉變換、拉普拉斯變換和z變換是信號處理中重要的數學工具。傅里葉變換用于將一個連續時間信號轉換為頻域表示;拉普拉斯變換則用于將一個連續時間信號轉換為復平面
2023-09-07 16:38:58 319
319 地理解和處理信號、圖像等復雜數據。 傅里葉變換是一種將信號(通常是函數)在頻域和時域之間相互轉換的數學方法,其核心思想是將一個函數拆分為各個不同頻率的正弦波的疊加。傅里葉變換可以被用來分析離散的非周期性函數
2023-09-07 16:35:07 836
836 傅氏變換和傅里葉變換的區別聯系 傅氏變換和傅里葉變換是信號處理中常用的兩種變換方法,它們有著不同的作用和特點。傅氏變換主要應用于連續時間信號的頻域分析,而傅里葉變換則主要用于離散時間信號的頻域分析
2023-09-07 16:35:05 195
195 傅里葉變換的本質及物理意義 常用傅里葉變換性質 傅里葉變換是一種重要的數學工具,通過將一個復雜的函數表示為一系列簡單的正弦余弦函數之和,可以在許多領域應用,包括信號處理、圖像處理、物理學等。在本文
2023-09-07 16:30:33 544
544 是將一個時域信號分解成一組頻域的正弦和余弦波的方法,這些波可以以復數形式表示。它通過將信號拆分成不同頻率的正弦和余弦波來分析信號的頻率特征,從而在頻域中描述信號。傅里葉變換適用于周期信號和非周期性信號,但在
2023-09-07 16:29:45 424
424 傅里葉變換時域平移怎么理解? 傅里葉變換是一種非常重要的數學工具,在信號處理、圖像處理、通信技術等領域中廣泛應用。其中,時域平移是傅里葉變換中一個重要的概念,需要深入理解。 時域平移的基本概念 時域
2023-09-07 16:29:40 330
330 傅里葉變換頻移公式 傅里葉變換是一種將信號從時域轉換到頻域的數學工具。它可以將一個信號分解成一系列正弦和余弦波的和,這些正弦和余弦波的振幅和相位可以描述信號在頻域中的特性。傅里葉變換是數字信號處理
2023-09-07 16:29:36 451
451 短時傅里葉變換特點 短時傅里葉變換的意義? 短時傅里葉變換(Short-time Fourier Transform, STFT)是一種時頻分析方法,它把信號在時間和頻率上進行分解,可以對信號的短時
2023-09-07 16:23:22 441
441 傅里葉變換的時移特性 傅里葉變換是一種非常重要的數學工具,可以將任何周期性信號或非周期性信號進行頻域分析,從而在通信、電子工程等領域中得到廣泛應用。傅里葉變換能夠將信號從時域(時間域)轉換到頻域
2023-09-07 16:23:19 739
739 對圖像進行傅里葉變換的意義 傅里葉變換是一種將一個信號分解成其頻率分量的方法,它在信號處理、圖像處理、電信領域、計算機視覺領域等方面都有著廣泛的應用。在圖像處理領域中,傅里葉變換可以將圖像從空間域
2023-09-07 16:18:56 353
353 傅里葉變換基本性質 傅里葉變換本質 傅里葉變換的應用 傅里葉變換是現代數學、物理學、工程學等領域中非常重要的一種數學工具和基本理論。在信號處理、圖像處理、通信技術、音樂分析、光學、醫學、天氣預報等
2023-09-07 16:18:49 2334
2334 傅里葉變換通俗理解 對傅里葉變換的理解? 傅里葉變換是一種數學工具,它可以將一個函數從時域(時間域)轉換到頻域(頻率域)。在數學、物理學、工程學和計算機科學等領域它被廣泛應用,例如數字信號處理
2023-09-07 16:14:41 570
570 傅里葉變換的目的和意義 傅里葉變換幾何意義? 傅里葉變換是一種重要的數學工具和分析方法,它在信號處理、圖像處理、音頻處理等領域有著廣泛的應用。它的目的是將一個時域信號轉換為頻域信號,從而更好地理
2023-09-07 16:14:39 307
307 傅里葉變換十大公式 傅里葉變換的十大性質? 傅里葉變換是一種重要的數學工具,在許多領域中都有廣泛的應用。傅里葉變換可以將一個時域信號轉化為頻域信號,分析不同頻率成分在信號中的占比情況。由于傅里葉變換
2023-09-07 16:14:36 1210
1210 傅里葉變換對信號處理的意義? 傅里葉變換是一種基本的數學工具,它經常用于信號處理中。在這篇文章中,我們將探討傅里葉變換的意義和應用。 傅里葉變換的定義是將一個函數表示為它的頻域表示。傅里葉變換將
2023-09-07 16:14:33 252
252 傅里葉變換有多偉大?傅里葉變換告訴我們如何解決問題? 傅里葉變換是一種數學工具,它可以將一個函數分解成一系列振幅和相位的頻率,這些頻率在某些領域 (如信號處理、圖像處理和物理學等)中被廣泛
2023-09-07 16:14:31 165
165 傅里葉變換的意義和理解 傅里葉變換是一種將一個信號在頻域中進行分解的數學工具,它將一個信號分解為不同頻率的正弦和余弦波的疊加。傅里葉變換的基本概念源于法國數學家約瑟夫·傅里葉,而其在現代通信、圖像
2023-09-07 16:08:42 3549
3549 在計算傅里葉變換之前對信號去趨勢是一種常見的做法,特別是在處理時間序列時。在這篇文章中,我將從數學和視覺上展示信號去趨勢是如何影響傅里葉變換的。
2023-08-16 15:26:23 333
333 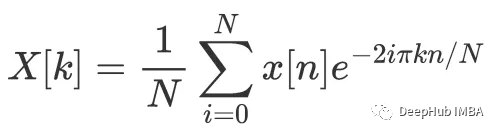
對于一個離開課堂十余年的射頻工程師來說,傅里葉變換已經不知道埋藏在腦子里的那個角落,或者根本就沒在腦子里停留過。但無論如何,傅里葉變換對現在通信的重要性還是不言而語。當我們已經習慣用頻域去描述一個信號的時候,你可曾思考過其真實的樣子到底是什么? 為什么這幾個短短的頻譜就可以描述一個信號 ?
2023-08-10 09:55:51 341
341 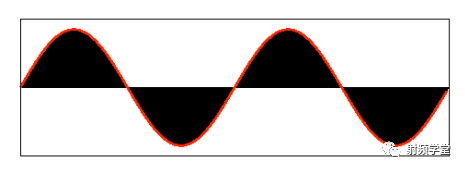
雖然周期信號不滿足絕對可積條件,但認為沖激函數有意義下絕對可積稱為不必要的限制
頻移特性——余弦信號(周期)的傅里葉變換——導出其余信號的頻譜函數
2023-08-09 15:06:46 342
342 
從上一講我們知道,周期信號的幅度譜和相位譜是在kω0(k=0,±1,±2,……)上離散的點取值,那么,ω0也可以表示為離散點的間隔,記作?ω。
2023-08-09 14:16:34 531
531 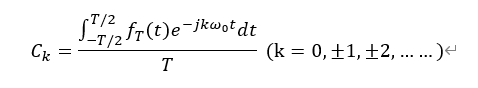
傅里葉變換是將按時間或空間采樣的信號與按頻率采樣的相同信號進行關聯的數學公式。
2023-07-19 17:47:30 1830
1830 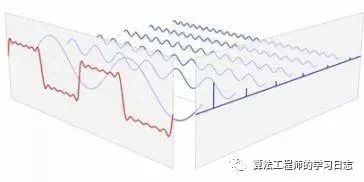
學習傅里葉變換需要面對大量的數學公式,數學功底較差的同學聽到傅里葉變換就頭疼
2023-07-07 14:15:10 217
217 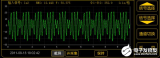
在實際中,通常會遇到按非正弦規律變化的信號,另外,如果電路存在非線性元件,即使在正弦信號的作用下也會產生非正弦周期的響應。非正弦信號分為周期和非周期兩種。傅里葉變換主要用于研究周期信號的電路響應。
2023-03-10 10:45:39 985
985 
在實際中,通常會遇到按非正弦規律變化的信號,另外,如果電路存在非線性元件,即使在正弦信號的作用下也會產生非正弦周期的響應。非正弦信號分為周期和非周期兩種。傅里葉變換主要用于研究周期信號的電路響應。
2023-03-02 14:16:23 2034
2034 
傅里葉變化只能對能量有限的信號進行變換(也就是可以收斂的信號),無法對能量無限的信號進行變換(無法收斂),因此,拉普拉斯應運而生,在原先的傅里葉變換公式中乘以一個衰減因子,使得無限能量的信號也能進行時頻變換。
2022-11-28 11:00:23 1013
1013 傅里葉變換是一種在各個領域都經常使用的數學工具。這個網站將為你介紹傅里葉變換能干什么,為什么傅里葉變換非常有用,以及你如何利用傅里葉變換干漂亮的事。
2022-07-10 10:37:53 1341
1341 的方式,本文提出了一種利用離散短時傅里葉變換(DSTFT)在時域和頻域解調2FSK信號的新方法。 2 利用DSTFT方法解調2FSK信號 2.1 離散短時傅里葉變換 離散短時傅里葉變換定義為: 其中:x
2009-10-23 10:41:14
周期矩陣脈沖信號傅里葉變換問題求解
2021-06-26 14:49:06 0
0 傅里葉變換在物理學、數論、組合數學、信號處理、概率論、統計學、密碼學、聲學、光學、海洋學、結構動力學等領域都有著廣泛的應用(例如在信號處理中,傅里葉變換的典型用途是將信號分解成幅值分量和頻率分量
2020-11-17 10:38:00 1
1 原信號的不同類型,傅里葉變換可以分為四種類別: (1)非周期性連續信號傅里葉變換 (2)周期性連續信號傅里葉級數 (3)非周期性離散信號離散時域傅里葉變換 (4)周期性離散信號離散傅里葉變換 快速傅里葉變換(FFT),是利用計算機計算離散傅里葉
2020-11-09 16:52:40 12009
12009 
學習傅里葉變換需要面對大量的數學公式,數學功底較差的同學聽到傅里葉變換就頭疼。事實上,許多數學功底好的數字信號處理專業的同學也不一定理解傅里葉變換的真實含義,不能做到學以致用 事實上,傅里葉變換
2020-10-10 18:03:17 21666
21666 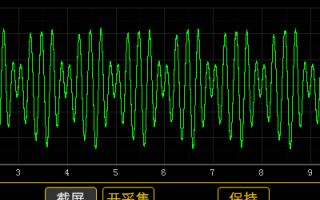
傅里葉變換是數字信號處理領城種很重要的算法。傅里葉表明:任何連續測量的時序或信號,都可以表示為不同頻率的正弦波信號的無限疊加。而根據該原理的傅里葉變換算法利用直接測量到的原始信號,以累加方式來計算該
2019-04-30 08:00:00 2
2 連續時間信號的頻域分析,是本課程最為重要的內容之一,也是考試的重點。包括三方面內容:周期信號的傅里葉級數、非周期信號的傅里葉變換、時域抽樣。本文對前兩個內容進行較為詳細的總結。
2018-05-19 09:15:28 50134
50134 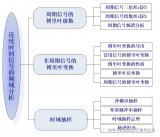
主要內容:
1.傅里葉變換
2.傅里葉變換的特殊形式
3.傅里葉變換的物理意義
4.傅里葉變換存在的條件
2018-03-05 11:08:04 3
3 主要內容:
1.正弦信號的傅里葉變換
2.一般周期信號的傅里葉變換
3.如何由F0(ω)求F(nω1)
4.單位沖激序列的傅氏變換
5.周期矩形脈沖序列的傅氏變換
2018-03-05 10:59:05 2
2 詳細講述傅里葉變換和小波變換原理
2018-01-16 14:34:42 9
9 小波變換與傅里葉變換有什么區別嗎?小波變換與傅里葉變換哪個好?我們通過小波變換與傅里葉變換的詳細解讀、小波變換與傅里葉變換的區別、傅里葉變換缺點方面來解析。
2018-01-13 11:02:22 13781
13781 
關于傅里葉變換變換?答:fourier變換是將連續的時間域信號轉變到頻率域;它可以說是laplace變換的特例,laplace變換是fourier變換的推廣,存在條件比fourier變換要寬,是將
2017-12-25 17:06:49 31378
31378 
針對偽隨機(PN)碼調制的多普勒激光雷達中固有的對外差信號不能等間隔采樣的問題,提出一種新的非均勻采樣信號的離散傅里葉變換(DFT)方法。首先,給出距離速度同步測量多普勒激光雷達系統模型,指出對外
2017-12-23 11:40:34 0
0 抽樣信號的傅里葉變換
2017-12-06 14:36:01 3
3 傅里葉變換的性質
2017-12-06 14:35:00 59
59 典型非周期信號的頻譜
2017-12-06 14:32:09 1
1 非周期信號的頻譜分析─傅里葉變換
2017-12-06 14:30:13 1
1 傅里葉級數對周期性現象做數學上的分析傅里葉變換可以看作傅里葉級數的極限形式,也可以看作是對周期現象進行數學上的分析。除此之外,傅里葉變換還是處理信號領域的一種很重要的算法。要想理解傅里葉變換算法的內涵,首先要了解傅里葉原理的內涵。
2017-11-24 14:32:42 37881
37881 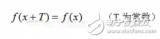
FT是傅里葉變換,它主要用于分析連續非周期信號,由于信號是非周期的,它必包含了各種頻率的信號,所以具有時域連續非周期對應頻域連續非周期的特點。
2017-10-23 10:50:45 10485
10485 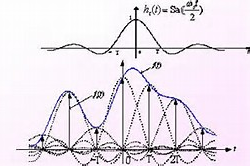
基于稀疏快速傅里葉變換的信號壓縮處理_劉清華
2017-02-27 19:07:37 0
0 第3章--離散傅里葉變換(DFT)
2016-12-28 14:23:30 2
2 信號與系統公式 常用的連續傅里葉變換安啊啊啊啊啊啊啊 啊啊
2016-04-26 10:41:13 18
18 該文提出了一種基于短時傅里葉變換的OFDM符號同步方法。該方法通過短時傅里葉變換得到OFDM信號的二維幅度譜,并提取其中的周期平穩時頻結構信息,估計出OFDM符號的無ISI時間區間,
2011-10-10 15:18:33 41
41 對于高頻信號和高頻噪聲干擾相混疊的信號,采用小波變換去除噪聲可以避免用傅里葉變換去噪帶來的信號折損。對于噪聲頻率固定的平穩信號,在對信號進行傅里葉變換后使用濾波器
2011-03-18 16:47:24 425
425 離散傅里葉變換是一種在時域和頻域均離散的傅里葉變換.
2011-02-23 09:30:10 49
49 基于小波變換的故障診斷信號非平穩性分析
從工程角度,解釋小波變換的實際含義,并將其與傳統的傅里葉變換分析方法作比較,通過比較兩種基函數的時頻窗,顯示
2010-02-22 17:08:46 24
24 序列的傅里葉變換(DTFT) :DTFT:Discrete-time Fourier transform為研究離散時間系統的頻率響應作準備,從抽樣信號的傅里葉變換引出:二.傅氏變換、拉氏變換、z變換的關系1. 三
2009-09-30 19:38:25 36
36 一、虛指數信號和正余弦信號的傅立葉變換 二、一般周期信號的傅立葉變換三、傅立葉系數與傅立葉變換的關系
2009-09-16 08:46:27 36
36 離散傅里葉變換及其快速算法離散傅里葉變換 (Discrete Fourier Transform,DFT)是時間函數是離散的,而且頻譜函數也是離散的變換。3. 1 討論周期序列的 傅里葉級數及其性質。
2008-10-30 12:54:54 33
33 從本章開始由時域轉入變換域分析,首先討論傅里葉變換。傅里葉變換是在傅里葉級數正交函數展開的基礎上發展而產生的,這方面的問題也稱為傅里葉分析(頻域分析)。將信號
2008-08-05 11:49:37 50
50 傅里葉變換公式
2007-11-29 12:52:35 494
494 傅里葉變換詳解
2007-11-29 12:48:01 4
4 什么是傅里葉變換
傅里葉變換(Transformée de Fourier)是一種積分變換。
因其基本思想首先
2007-11-29 12:46:55 7717
7717 
![]() 趨于零,即譜線從離散轉向連續,而其振幅值則趨于零,信號中各分量都變為無窮小。盡管各頻率分量從絕對值來看都趨于無窮小,但其相對大小卻是不相同的。為區別這種相對大小,在周期T趨于無窮大時,求
趨于零,即譜線從離散轉向連續,而其振幅值則趨于零,信號中各分量都變為無窮小。盡管各頻率分量從絕對值來看都趨于無窮小,但其相對大小卻是不相同的。為區別這種相對大小,在周期T趨于無窮大時,求![]() 的極限,并定義此極限值為非周期函數的頻譜函數
的極限,并定義此極限值為非周期函數的頻譜函數![]() ,即:
,即: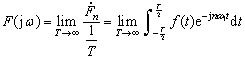
![]() 時,,
時,,![]() 轉化為,即離散的頻譜轉為連續頻譜,上式可改為:
轉化為,即離散的頻譜轉為連續頻譜,上式可改為:![]() ??????? ??(6-4-1)
??????? ??(6-4-1)![]() ,可由上式求出其頻譜函數,同理若已知非周期信號頻譜函數
,可由上式求出其頻譜函數,同理若已知非周期信號頻譜函數![]() ,則也可求出其時域表達式。其計算式為:
,則也可求出其時域表達式。其計算式為:![]() ??????? (6-4-2)
??????? (6-4-2)![]() 轉換為頻域的頻譜函數信號,稱為傅里葉正變換。而式6-4-2是把頻域信號
轉換為頻域的頻譜函數信號,稱為傅里葉正變換。而式6-4-2是把頻域信號![]() 變換為時域信號,稱為傅里葉逆變換。進行傅里葉變換的函數需滿足狄里赫里條件和絕對可積條件。
變換為時域信號,稱為傅里葉逆變換。進行傅里葉變換的函數需滿足狄里赫里條件和絕對可積條件。![]() ,并作振幅頻譜與相位頻譜圖。
,并作振幅頻譜與相位頻譜圖。![]()
![]()
![]() 。如果脈沖寬度變窄,即值變小,則信號主要頻率分量所占的頻率范圍就變大。反之當脈沖變寬,值變大,則其主要頻率分量范圍就變小。對于一個較窄的脈沖信號,如果電路要使它通過,則電路的特性必須能使較大頻率范圍的所有信號都能通過。傅里葉變換在信號分析與處理中有重要意義。
。如果脈沖寬度變窄,即值變小,則信號主要頻率分量所占的頻率范圍就變大。反之當脈沖變寬,值變大,則其主要頻率分量范圍就變小。對于一個較窄的脈沖信號,如果電路要使它通過,則電路的特性必須能使較大頻率范圍的所有信號都能通過。傅里葉變換在信號分析與處理中有重要意義。 電子發燒友App
電子發燒友App








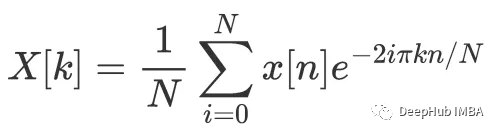


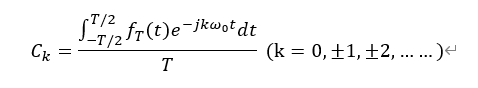





















評論