線性非時變系統定義給我們帶來了許多數學工具,也包含卷積積分,傅里葉變換和拉普拉斯變換。
2023-10-17 10:31:46 122
122 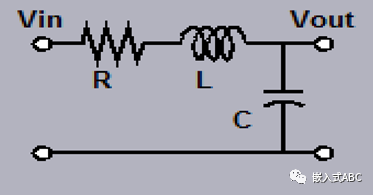
濾波器的響應可以用s域傳遞函數表示;變量s來自拉普拉斯變換,代表復雜的頻率。
2023-09-19 16:58:07 481
481 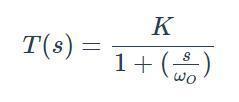
傅里葉變換與拉普拉斯變換的聯系解讀 傅里葉變換和拉普拉斯變換都是數學中非常重要的分析工具。它們都在不同的領域中發揮著重要作用。 傅里葉變換是一種將時間域信號轉換成頻率域信號的技術。它是通過將信號
2023-09-07 17:04:19 219
219 如何用拉普拉斯變換分析電路 拉普拉斯變換是通過一種特定的方法將時域中的一個信號轉化為復頻域中的一個函數,從而使得復雜的微分方程等可以變得更加簡單、易于求解。因此,它在電路分析中的應用非常廣泛,有助于
2023-09-07 16:39:04 305
305 傅里葉變換拉普拉斯變換和z變換的區別聯系 傅里葉變換、拉普拉斯變換和z變換是信號處理中重要的數學工具。傅里葉變換用于將一個連續時間信號轉換為頻域表示;拉普拉斯變換則用于將一個連續時間信號轉換為復平面
2023-09-07 16:38:58 319
319 拉普拉斯變換公式? 拉普拉斯變換公式是數學中極其重要的一種變換方式,它的應用領域非常廣泛,包括在信號處理、控制論、微分方程、電路分析和量子力學等領域中都有著廣泛的應用。本文將詳細介紹拉普拉斯變換公式
2023-09-07 16:38:53 518
518 拉普拉斯變換的意義 拉普拉斯變換是微積分中的一種重要方法,用于將時間域函數轉換為復平面的頻域函數。它是工程和科學中常用的一種數學工具,尤其是電路理論、信號處理和控制理論中。 拉普拉斯變換的意義可以
2023-09-07 16:35:08 940
940 傅里葉變換和拉普拉斯變換的區別聯系 傅里葉變換和拉普拉斯變換是數學中兩種具有重要意義的變換方式。它們都在信號處理、傳輸和控制領域被廣泛應用,能夠將時域信號轉換為頻域信號或復平面上的信號。 傅里葉變換
2023-09-07 16:29:45 424
424 拉普拉斯變換的頻移特性 拉普拉斯變換是一種重要的數學工具,在信號處理、控制理論、電路分析等領域廣泛應用。在這些應用中,頻移是一個常見的操作,即將信號在頻域上移動某個頻率。 拉普拉斯變換是一種復數變換
2023-09-07 16:29:43 141
141 第一部分 什么是卷積,卷積有什么用,什么是傅利葉變換,什么是拉普拉斯變換?
2023-04-12 10:58:53 923
923 之前的一階電路和二階電路的分析,所應用的方法是根據電路定理和元件的電壓,電流關系建立線性常微分方程,通過求解微分方程的解求得電路的時域響應,這種方法又稱為經典法。
2023-03-10 10:47:46 1532
1532 
所以對于高階系統,一般采用積分變換法,將時域函數變為頻域函數,從而將時域微分方程轉為頻域代數方程求解,求出頻域解后在還原為時域解。拉普拉斯變換是一種重要的積分變換。
2023-03-02 14:19:27 591
591 
傅里葉變化只能對能量有限的信號進行變換(也就是可以收斂的信號),無法對能量無限的信號進行變換(無法收斂),因此,拉普拉斯應運而生,在原先的傅里葉變換公式中乘以一個衰減因子,使得無限能量的信號也能進行時頻變換。
2022-11-28 11:00:23 1013
1013 數學變換是指數學函數從原向量空間在自身函數空間變換,或映射到另一個函數空間,或對于集合X到其自身(比如線性變換)或從X到另一個集合Y的可逆變換函數。
2022-07-23 17:45:10 1785
1785 
赫維賽德之所以這么做,是因為他的“物理直覺”告訴他這么做,就是這么硬。這顯然是一種開外掛的行為,因此也受到當時的主流數學家們們的攻訐,他們認為赫維賽德就是十足的“民科”,文章沒什么理論依據,自己在那空想呢。當然,赫維賽德也不是弱雞,科學家懟起人來,也是毫不含糊:“因為我不能理解消化過程就拒絕晚餐嗎?不,只要我滿意這個結果。”
2022-03-15 14:08:18 1611
1611 信號與系統.PDF書,講述了拉普拉斯變換、Z變換與傅里葉變換方便的知識,通俗易懂。
2022-01-07 09:21:05 5
5 拉普拉斯變換表下載
2021-12-30 09:47:12 4
4 從傅里葉級數、傅里葉變換推出拉普拉斯變換。
2021-06-23 16:25:27 5437
5437 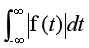
拉普拉斯變換.ppt以傅立葉變換為基礎的頻域分析方法的優點在于:它給出的結果有著清楚的物理意義 ,但也有不足之處,傅立葉變換只能處理符合狄利克雷條件的信號,而有些信號是不滿足絕對可積條件的,因而
2009-09-16 08:35:50
電子發燒友網為你提供通俗的角度看待拉普拉斯變換資料下載的電子資料下載,更有其他相關的電路圖、源代碼、課件教程、中文資料、英文資料、參考設計、用戶指南、解決方案等資料,希望可以幫助到廣大的電子工程師們。
2021-03-30 08:47:41 6
6 在知乎上看到一個問題,傅里葉變換、拉普拉斯變換、Z 變換的聯系是什么?為什么要進行這些變換?我覺得這是一個非常好的問題,貌似一下子也回答不上來,所以整理學習并分享一下。
2021-02-15 11:59:00 7844
7844 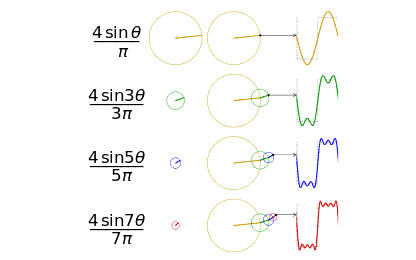
數學變換是指數學函數從原向量空間在自身函數空間變換,或映射到另一個函數空間,或對于集合X到其自身(比如線性變換)或從X到另一個集合Y的可逆變換函數。
2021-01-18 16:13:41 2976
2976 
傅里葉變換在物理學、數論、組合數學、信號處理、概率論、統計學、密碼學、聲學、光學、海洋學、結構動力學等領域都有著廣泛的應用(例如在信號處理中,傅里葉變換的典型用途是將信號分解成幅值分量和頻率分量
2020-11-17 10:38:00 1
1 本文檔的主要內容詳細介紹的是拉普拉斯變換的習題與詳解免費下載。
2020-09-28 08:00:00 0
0 本文檔的主要內容詳細介紹的是控制系統的數學模型拉普拉斯變換的詳細資料說明。
2020-06-09 08:00:00 0
0 Z變換和傅里葉變換之間有存在什么樣的關系呢?傅里葉變換的物理意義非常清晰:將通常在時域表示的信號,分解為多個正弦信號的疊加。
2019-09-29 07:05:00 5245
5245 傅里葉變換在物理學、數論、組合數學、信號處理、概率論、統計學、密碼學、聲學、光學、海洋學、結構動力學等領域都有著廣泛的應用(例如在信號處理中,傅里葉變換的典型用途是將信號分解成幅值分量和頻率分量)。
2019-03-08 15:01:06 5960
5960 本文檔的主要內容詳細介紹的是拉普拉斯變換電路理論練習題來做作看吧。
2018-11-27 08:00:00 15
15 拉普拉斯變換是工程數學中常用的一種積分變換,又名拉氏變換。拉氏變換是一個線性變換,可將一個有引數實數t(t≥ 0)的函數轉換為一個引數為復數s的函數。
2018-09-17 08:02:00 11315
11315 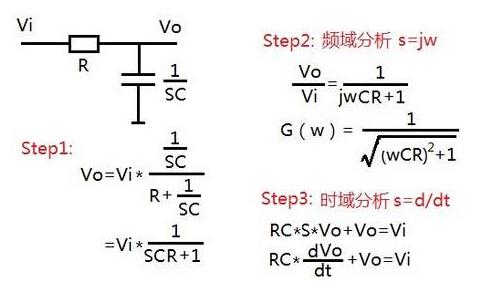
傅里葉變換與拉普拉斯變換的物理解釋及區別pdf文檔資料下載
2017-12-19 17:22:52 4
4 拉普拉斯變換是工程數學中常用的一種積分變換,又名拉氏變換。拉氏變換是一個線性變換,可將一個有參數實數t(t≥ 0)的函數轉換為一個參數為復數s的函數。拉普拉斯變換在許多工程技術和科學研究領域
2017-12-06 17:22:46 76342
76342 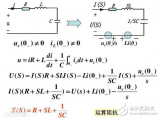
一種積分變換,它來源于函數的傅里葉積分表示。積分稱為? 的傅里葉積分。拉普拉斯變換是工程數學中常用的一種積分變換,又名拉氏變換。拉氏變換是一個線性變換,可將一個有參數實數t(t≥ 0)的函數轉換為一個參數為復數s的函數。
2017-12-05 19:10:02 83345
83345 
有些情形下一個實變量函數在實數域中進行一些運算并不容易,但若將實變量函數作拉普拉斯變換,并在復數域中作各種運算,再將運算結果作拉普拉斯反變換來求得實數域中的相應結果,在經典控制理論中,對控制系統的分析和綜合,都是建立在拉普拉斯變換的基礎上的。
2017-12-05 18:30:31 234698
234698 
傳遞函數是指零初始條件下線性系統響應(即輸出)量的拉普拉斯變換(或z變換)與激勵(即輸入)量的拉普拉斯變換之比。延遲環節從輸入開始后在0 ~ τ時間內沒有輸出,但t =τ之后,輸出完全等于輸入。
2017-11-29 16:40:18 61938
61938 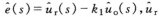
關于利用拉普拉斯變換求解系統初值問題書中只給出了一種比較簡單的情況,即時域函數在零時刻有界時的求解方法。很遺憾,對于在零時刻存在沖擊情況下的初值問題,這種方法并不適用。而這種問題又是大量存在的,所以
2017-11-16 11:02:22 5
5 自動化基礎知識--拉普拉斯變換的概念
2017-10-26 08:53:36 1
1 拉普拉斯變換及其應用拉普拉斯變換及其應用拉普拉斯變換及其應用拉普拉斯變換及其應用
2015-10-28 11:19:28 26
26 2014-09-06 22:26:19 5
5 2013-12-18 12:07:19 1
1 2012-06-06 15:14:45 30
30 應用拉普拉斯變換分析RLC電路:應用拉普拉斯變換分析R上c 電路,不需要確定積分常數,從而避免了時域求解微分方程確定積分常數的繁瑣計算。關鍵詞:拉普拉斯變換;RLC電路
2010-04-12 08:31:44 124
124 z變換與拉普拉斯變換的關系:一.z平面與s平面的映射關系二.z變換與拉式變換表達式之對應
2009-09-30 19:40:36 46
46 拉普拉斯變換視頻教程免費下載:一 拉普拉斯變換的定義 1、從絕對可積條件討論傅氏變換的問題,引入衰減因子的概念; 2、導出拉氏變換與逆變換公式; 3、單邊拉氏變換的概念;
2009-09-03 12:00:40 226
226 連續時間LTI系統的復頻域分析:連續時間LTI系統的復頻域分析一、用拉普拉斯變換法求解微分方程 1.拉普拉斯變換法的優點 2.微分方程的拉氏變換二、基于s域模型的電路分析 1.電阻元
2009-09-03 11:59:58 18
18 拉普拉斯變換的基本定理
本節介紹拉普拉斯變換(也稱為拉氏變換)的基本性質,了解掌握了這些性質,可以更加方便地求解各種拉普
2009-07-27 11:43:12 22114
22114 拉普拉斯變換教案:§13-1 拉普拉斯變換的定義§13-2 拉普拉斯變換的基本性質§13-3 拉普拉斯反變換的部分分式展開§13-4 運算電路§13-5 應用拉普拉斯變換法分析線性電路
2009-07-09 11:37:56 71
71 拉普拉斯變換及其應用:1.1基本要求1,熟悉拉氏變換的基本法則2,熟練掌握典型函數的拉氏變換式。3,掌握用拉氏變換求解微分方程初值問題的思路。4,熟練掌握求有理分式
2009-07-08 11:43:00 128
128 什么是拉普拉斯變換
拉普拉斯變換:拉普拉斯變換(英文:Laplace Transform),是工程數學中常用的一種積分變換。如果定義: f(t),是一個關于t,的函數,使得當t<0
2009-07-08 11:42:30 4963
4963 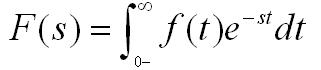
拉普拉斯變換公式
1、拉氏變換定義
2009-07-08 11:36:57 12239
12239 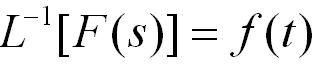
1、元件的復頻域模型2、應用拉氏變換分析線性動態電路 R和C的復頻域模型13-1 有關知識的復習13-2 應用拉氏變換分析電路
2009-07-08 10:33:21 67
67 介紹了一種變換近似方法,該方法通過變換近似獲得重尾分布的拉普拉斯變換,解決了不存在拉普拉斯變換分布的信源排隊等待時間分析問題,為實際網絡排隊緩沖器的設計提供
2009-02-28 16:33:18 20
20 動態電路的復頻域分析 6.1 拉普拉斯變換及其性質 6.2 拉普拉斯反變換 6.3 電路基本定律及電路元件的復頻域形式 6.4 應用拉普拉斯變換分
2008-12-04 17:55:29 40
40
![]() 的區間。這就相當于將函數乘上了單位階躍函數,即:
的區間。這就相當于將函數乘上了單位階躍函數,即:![]()
![]() 在區間
在區間![]() 內絕對可積,則它的傅里葉變換為:
內絕對可積,則它的傅里葉變換為: ??? ?(式9-1-1)
??? ?(式9-1-1)![]() ,記為:
,記為:![]()
 電子發燒友App
電子發燒友App






























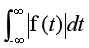






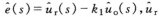
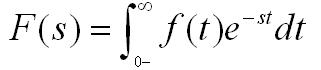
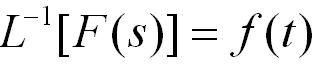










評論