一、動態(tài)規(guī)劃算法簡介
動態(tài)規(guī)劃算法是通過拆分問題,定義問題狀態(tài)和狀態(tài)之間的關系,使得問題能夠以遞推(或者說分治)的方式去解決。
1.基本思想與策略
動態(tài)規(guī)劃算法的基本思想與分治法類似,也是將待求解的問題分解為若干個子問題(階段),按順序求解子階段,前一子問題的解,為后一子問題的求解提供了有用的信息。在求解任一子問題時,列出各種可能的局部解,通過決策保留那些有可能達到最優(yōu)的局部解,丟棄其他局部解。依次解決各子問題,最后一個子問題就是初始問題的解。由于動態(tài)規(guī)劃解決的問題多數(shù)有重疊子問題這個特點,為減少重復計算,對每一個子問題只解一次,將其不同階段的不同狀態(tài)保存在一個二維數(shù)組中。
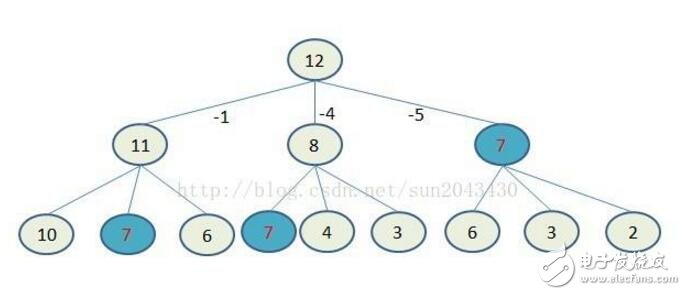
2.適用情況
能采用動態(tài)規(guī)劃求解的問題的一般要具有3個性質:
(1)最優(yōu)化原理:如果問題的最優(yōu)解所包含的子問題的解也是最優(yōu)的,就稱該問題具有最優(yōu)子結構,即滿足最優(yōu)化原理。
(2)無后效性:即某階段狀態(tài)一旦確定,就不受這個狀態(tài)以后決策的影響。也就是說,某狀態(tài)以后的過程不會影響以前的狀態(tài),只與當前狀態(tài)有關。
(3)有重疊子問題:即子問題之間是不獨立的,一個子問題在下一階段決策中可能被多次使用到。(該性質并不是動態(tài)規(guī)劃適用的必要條件,但是如果沒有這條性質,動態(tài)規(guī)劃算法同其他算法相比就不具備優(yōu)勢)
3.算法實現(xiàn)
動態(tài)規(guī)劃的主要難點在于理論上的設計,也就是上面4個步驟的確定,一旦設計完成,實現(xiàn)部分就會非常簡單。使用動態(tài)規(guī)劃求解問題,最重要的就是確定動態(tài)規(guī)劃三要素:
(1)問題的階段
(2)每個階段的狀態(tài)
(3)從前一個階段轉化到后一個階段之間的遞推關系。
遞推關系必須是從次小的問題開始到較大的問題之間的轉化,從這個角度來說,動態(tài)規(guī)劃往往可以用遞歸程序來實現(xiàn),不過因為遞推可以充分利用前面保存的子問題的解來減少重復計算,所以對于大規(guī)模問題來說,有遞歸不可比擬的優(yōu)勢,這也是動態(tài)規(guī)劃算法的核心之處。
確定了動態(tài)規(guī)劃的這三要素,整個求解過程就可以用一個最優(yōu)決策表來描述,最優(yōu)決策表是一個二維表,其中行表示決策的階段,列表示問題狀態(tài),表格需要填寫的數(shù)據(jù)一般對應此問題的在某個階段某個狀態(tài)下的最優(yōu)值(如最短路徑,最長公共子序列,最大價值等),填表的過程就是根據(jù)遞推關系,從1行1列開始,以行或者列優(yōu)先的順序,依次填寫表格,最后根據(jù)整個表格的數(shù)據(jù)通過簡單的取舍或者運算求得問題的最優(yōu)解。
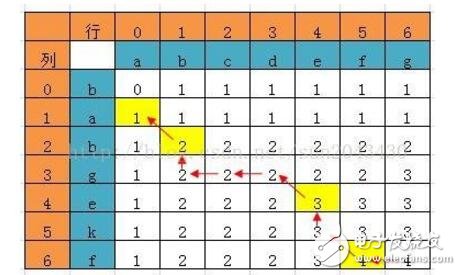
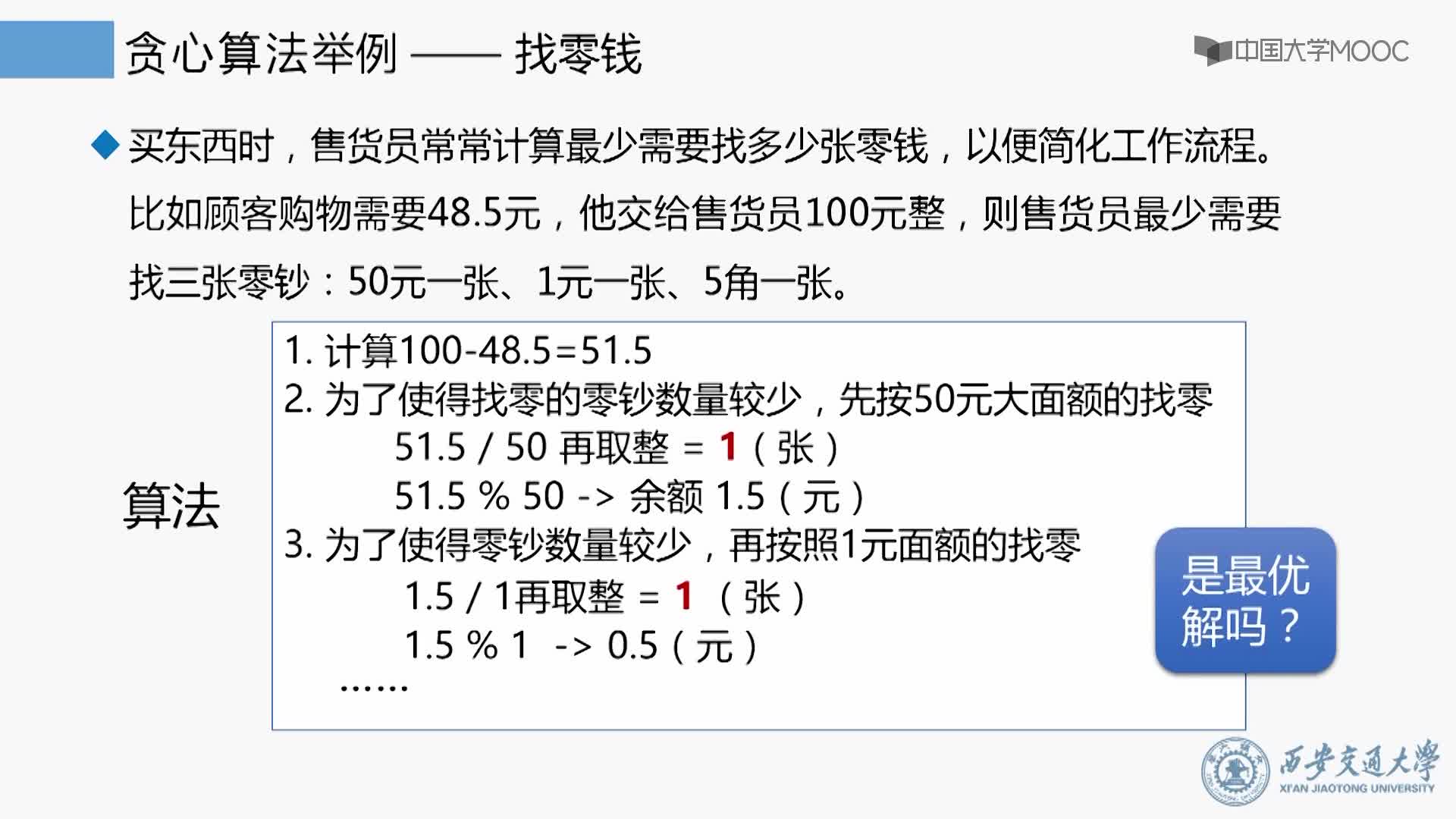
二、貪心算法簡介
貪心算法(又稱貪婪算法)是指,在對問題求解時,總是做出在當前看來是最好的選擇。也就是說,不從整體最優(yōu)上加以考慮,他所做出的是在某種意義上的局部最優(yōu)解。貪心算法不是對所有問題都能得到整體最優(yōu)解,關鍵是貪心策略的選擇,選擇的貪心策略必須具備無后效性,即某個狀態(tài)以前的過程不會影響以后的狀態(tài),只與當前狀態(tài)有關。
1.基本要素
貪心選擇
貪心選擇是指所求問題的整體最優(yōu)解可以通過一系列局部最優(yōu)的選擇,即貪心選擇來達到。這是貪心算法可行的第一個基本要素,也是貪心算法與動態(tài)規(guī)劃算法的主要區(qū)別。貪心選擇是采用從頂向下、以迭代的方法做出相繼選擇,每做一次貪心選擇就將所求問題簡化為一個規(guī)模更小的子問題。對于一個具體問題,要確定它是否具有貪心選擇的性質,我們必須證明每一步所作的貪心選擇最終能得到問題的最優(yōu)解。通常可以首先證明問題的一個整體最優(yōu)解,是從貪心選擇開始的,而且作了貪心選擇后,原問題簡化為一個規(guī)模更小的類似子問題。然后,用數(shù)學歸納法證明,通過每一步貪心選擇,最終可得到問題的一個整體最優(yōu)解。
最優(yōu)子結構
當一個問題的最優(yōu)解包含其子問題的最優(yōu)解時,稱此問題具有最優(yōu)子結構性質。運用貪心策略在每一次轉化時都取得了最優(yōu)解。問題的最優(yōu)子結構性質是該問題可用貪心算法或動態(tài)規(guī)劃算法求解的關鍵特征。貪心算法的每一次操作都對結果產生直接影響,而動態(tài)規(guī)劃則不是。貪心算法對每個子問題的解決方案都做出選擇,不能回退;動態(tài)規(guī)劃則會根據(jù)以前的選擇結果對當前進行選擇,有回退功能。動態(tài)規(guī)劃主要運用于二維或三維問題,而貪心一般是一維問題。
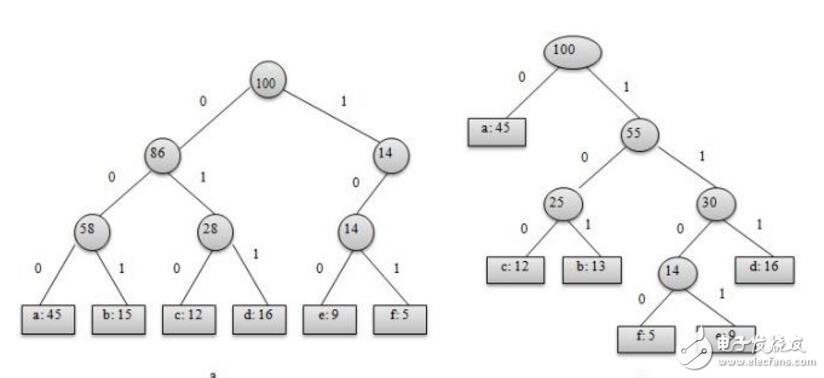
2.算法特性
貪婪算法可解決的問題通常大部分都有如下的特性:
隨著算法的進行,將積累起其它兩個集合:一個包含已經被考慮過并被選出的候選對象,另一個包含已經被考慮過但被丟棄的候選對象。
有一個函數(shù)來檢查一個候選對象的集合是否提供了問題的解答。該函數(shù)不考慮此時的解決方法是否最優(yōu)。
還有一個函數(shù)檢查是否一個候選對象的集合是可行的,也即是否可能往該集合上添加更多的候選對象以獲得一個解。和上一個函數(shù)一樣,此時不考慮解決方法的最優(yōu)性。
選擇函數(shù)可以指出哪一個剩余的候選對象最有希望構成問題的解。
最后,目標函數(shù)給出解的值。
為了解決問題,需要尋找一個構成解的候選對象集合,它可以優(yōu)化目標函數(shù),貪婪算法一步一步的進行。起初,算法選出的候選對象的集合為空。接下來的每一步中,根據(jù)選擇函數(shù),算法從剩余候選對象中選出最有希望構成解的對象。如果集合中加上該對象后不可行,那么該對象就被丟棄并不再考慮;否則就加到集合里。每一次都擴充集合,并檢查該集合是否構成解。如果貪婪算法正確工作,那么找到的第一個解通常是最優(yōu)的。
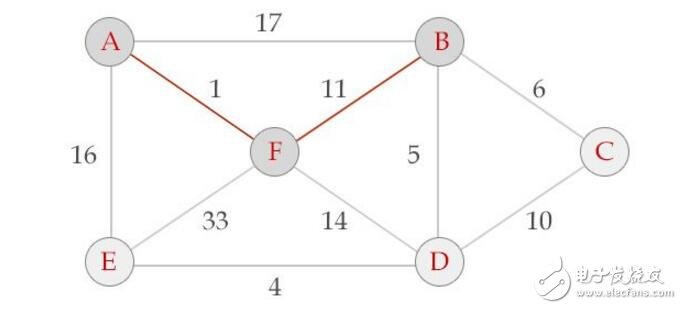
三、動態(tài)規(guī)劃算法和貪心算法的區(qū)別與聯(lián)系
背景介紹:這兩種算法都是選擇性算法,就是從一個候選集合中選擇適當?shù)脑丶尤虢饧稀?/p>
貪心算法的選擇策略即貪心選擇策略,通過對候選解按照一定的規(guī)則進行排序,然后就可以按照這個排好的順序進行選擇了,選擇過程中僅需確定當前元素是否要選取,與后面的元素是什么沒有關系。
動態(tài)規(guī)劃的選擇策略是試探性的,每一步要試探所有的可行解并將結果保存起來,最后通過回溯的方法確定最優(yōu)解,其試探策略稱為決策過程。
主要不同:兩種算法的應用背景很相近,針對具體問題,有兩個性質是與算法選擇直接相關的,最優(yōu)子結構性質和貪心選擇性質。
最優(yōu)子結構性質是選擇類最優(yōu)解都具有的性質,即全優(yōu)一定包含局優(yōu),上一次選擇最短路線的例子已經對此作了說。
當時我們也提到了貪心選擇性質,滿足貪心選擇性質的問題可用貪心算法解決,不滿足貪心選擇性質的問題只能用動態(tài)規(guī)劃解決。可見能用貪心算法解決的問題理論上都可以利用動態(tài)規(guī)劃解決,而一旦證明貪心選擇性質,用貪心算法解決問題比動態(tài)規(guī)劃具有更低的時間復雜度和空間復雜度。
貪心算法:
1.貪心算法中,作出的每步貪心決策都無法改變,因為貪心策略是由上一步的最優(yōu)解推導下一步的最優(yōu)解,而上一部之前的最優(yōu)解則不作保留。
2.貪心法正確的條件是:每一步的最優(yōu)解一定包含上一步的最優(yōu)解。
動態(tài)規(guī)劃算法:
1.全局最優(yōu)解中一定包含某個局部最優(yōu)解,但不一定包含前一個局部最優(yōu)解,因此需要記錄之前的所有最優(yōu)解
2.動態(tài)規(guī)劃的關鍵是狀態(tài)轉移方程,即如何由以求出的局部最優(yōu)解來推導全局最優(yōu)解
3.邊界條件:即最簡單的,可以直接得出的局部最優(yōu)解
所謂貪心選擇性質是指所求問題的整體最優(yōu)解可以通過一系列局部最優(yōu)的選擇,即貪心選擇來達到。這是利用貪心算法求解最優(yōu)解的第一個基本要素,也是貪心算法與動態(tài)規(guī)劃算法的主要區(qū)別。
在貪心算法中,作出的每步貪心決策都無法改變,因為貪心策略是由上一步的最優(yōu)解推導下一步的最優(yōu)解,而上一部之前的最優(yōu)解則不作保留。并且,每一步的最優(yōu)解一定包含上一步的最優(yōu)解。
而在動態(tài)規(guī)劃算法中,全局最優(yōu)解中一定包含某個局部最優(yōu)解,但不一定包含前一個局部最優(yōu)解,因此需要記錄之前的所有最優(yōu)解。動態(tài)規(guī)劃的關鍵是狀態(tài)轉移方程,即如何由以求出的局部最優(yōu)解來推導全局最優(yōu)解。也就是說,把一個復雜問題分解成一塊一塊的小問題,每一個問題得到最優(yōu)解,再從這些最優(yōu)解中獲取更優(yōu)的答案。
?
 電子發(fā)燒友App
電子發(fā)燒友App






























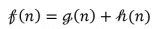












評論