閥值化處理就是當灰度值低于一個值(閥值,根據你的需要設定)時,讓其成為一個小的值;當灰度值大于一個值(閥值)時,讓其成為一個大的值。
比如:灰度在0-255, 當灰度小于128時賦值為0,大于128時賦值為255,即亮的地方更亮,暗的地方更暗。即實現了閥值分割。這樣圖像就黑白分明,對比度加大了。
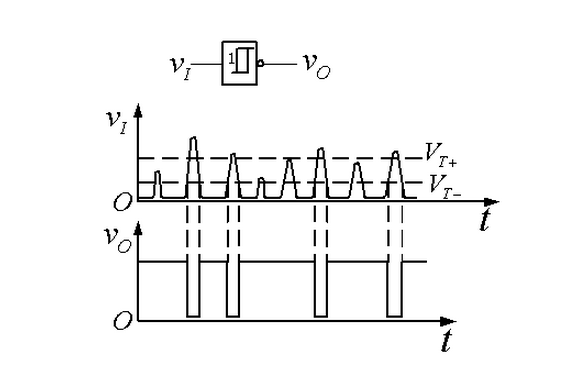
硬閥值:是被檢測數據所不能逾越的閥值。
軟閥值:則規定被檢測數據的變動范圍。
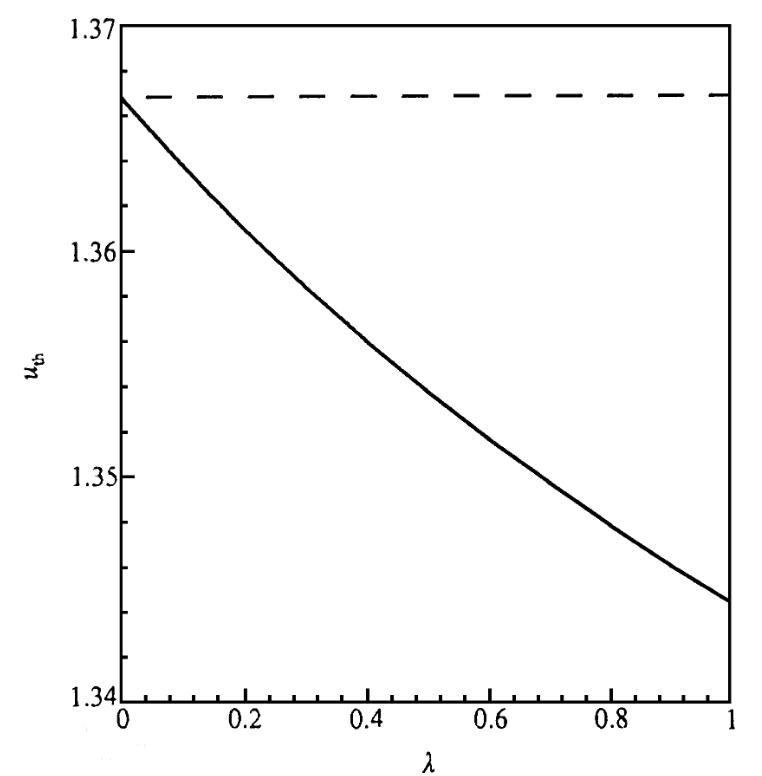
軟閾值,硬閾值及當今各種閾值計算方法和閾值函數處理方法的性能
小波閾值去噪,比較了軟閾值,硬閾值及當今各種閾值計算方法和閾值函數處理方法的性能,通過信噪比及均方差的比較,得出各種的算法的優劣。
clear;clc;
從程序的運行結果來看,文獻1,3,4的去噪效果比較好
其中文獻4對高信噪比的的情況不是很好,在高信噪比時,軟硬閾值的效果最好
測試數據的選取
fun=‘blocks’;
snr=5;
jN=5; 分解的層數
N=13; 數據長度為2^N
[x,s]=wnoise(4,N,sqrt(snr));
ps=sum(x.^2)/length(x);
sigma_noise=abs(sqrt(ps/(10^(snr/10))));
noise=sigma_noise*randn(1,length(x));noise噪聲的方差是(sigma_noise.^2)
s=x+noise;
figure,
subplot(211);plot(x);
subplot(212);plot(s);
subplot(211);plot(x);title(‘純凈信號x’);
subplot(212);plot(s);title(‘混合信號x’);
調幅信號,純凈信號
tic;
fs=5e+6; 采樣率50M
ts=1/fs;
fc=10.7e+6; 載頻10.7M
t0=2; 數據長度N=t0*fs;
t=[0:ts:t0]; 模擬信號的數字化
m=sinc(100*t); 消息信號
c=cos(2*pi*fs.*t);載波信號
x=m.*c;
N=t0*fs;
toc;
t0=.2; signal duration
ts=0.001; sampling interval
fc=250; carrier frequency
snr=20; SNR in dB (logarithmic)
fs=1/ts; sampling frequency
t=[-t0/2:ts:t0/2]; time vector
m=sinc(100*t); the message signal
c=cos(2*pi*fc.*t); the carrier signal
x=m.*c; the DSB-AM modulated signal
N=t0*fs;
-------------------------BPSK信號,數字調制-----------------------------------
codes=6; 碼元個數,即輸入調制信號的長度
sigma=1; 調制信號的幅度
fs=600e3; 采樣率600KHz
fb=1e3; 波特率1KHz,fb表示對輸入調制信號的采樣率
fc=100e3; 載頻100KHz
Modulate=2; 為選擇調制方式
N0=fs/fb; 一個碼元周期內的采樣點數,一個輸入信號長度內的采樣點數
N=N0*codes; 總的采樣點數(已調信號的長度)
p0=pi*rand(1,1); 產生初始相位
symbols=randint(1,codes,[0,1]); 產生基帶碼元
x_B = ones(N0,1)*symbols;
x_BB = x_B(:)‘; 根據波特率要求產生碼元
signal_base = x_BB; 產生基帶信號
signal=sigma*dmod(symbols,fc,fb,[fs p0],’psk‘,Modulate);
產生psk調制信號,p0是載頻的初始相位
x=si
gnal;
-------------------------加入指定強度的噪聲---------------------------------
snr=5;
ps=sum(x.^2)/N;
sigma_noise=abs(sqrt(ps/(10^(snr/10))));
nn=randn(1,N);
enn=sum(nn)/N; 隨機數nn的均值
nn=nn-enn; 使nn均值為0
noise=sigma_noise*nn;
s=x+noise;
wname=’db7‘;
jN=6; 分解的層數
[c,l]=wavedec(s,jN,wname);
snrs=20*log10(norm(x)/norm(s-x));
mmses=mmse(s-x);
高頻分量的索引
first = cumsum(l)+1;
first1=first;
first = first(end-2:-1:1);
ld = l(end-1:-1:2);
last = first+ld-1;
軟閾值與硬閾值
cxdsoft=c;
cxdhard=c;
for j=1:jN j是分解尺度
flk = first(j):last(j);flk是di在c中的索引
thr(j)=sqrt(log(length(flk)))/log(j+1);
for k=0:(length(flk)-1)k是位移尺度
djk=c(first(j)+k);為了簡化程序
djk2=c(first(j)+k);
absdjk=abs(djk);
thr1=thr(j);
閾值處理
if absdjkthr1
djk=djk-thr1/exp((djk-thr1)/n);
else
djk=djk+thr1/exp((-djk-thr1)/n);
end
cxd51(first(j)+k)=djk;
end
end
新方法二
cxd52=c;
for j=1:jN
flk = first(j):last(j);
for k=0:(length(flk)-1)
djk=c(first(j)+k);為了簡化程序
absdjk=abs(djk);
thr1=thr(j);
if absdjkthr1
djk=djk-thr1+thr1/(2*b+1);
else
djk=djk+thr1-thr1/(2*b+1);
end
cxd53(first(j)+k)=djk;
end
end
新方法四
cxd54=c;
for j=1:jN
flk = first(j):last(j);
for k=0:(length(flk)-1)
djk=c(first(j)+k);為了簡化程序
absdjk=abs(djk);
thr1=thr(j);
bb=(2*aa+1+m*sqrt((2*aa+1).^2-pi.^2))/(pi*thr1.^(2*n+1));
kk=(1+(bb*thr1.^(2*n+1)).^2)/((2*a+1)*bb*thr1.^(2*n));
if absdjkthr1
djk=djk-thr1+kk*atan(bb*djk.^(2*aa+1));
else
djk=djk+thr1-kk*atan(bb*djk.^(2*aa+1));
end
cxd54(first(j)+k)=djk;
end
end
信號重構
snew51=waverec(cxd51,l,wname);
snew52=waverec(cxd52,l,wname);
snew53=waverec(cxd53,l,wname);
snew54=waverec(cxd54,l,wname);
信噪比及均方差分析
snry51=20*log10(norm(x)/norm(snew51-x));
snry52=20*log10(norm(x)/norm(snew52-x));
snry53=20*log10(norm(x)/norm(snew53-x));
snry54=20*log10(norm(x)/norm(snew54-x));
mmsey51=mmse(snew51-x);
mmsey52=mmse(snew52-x);
mmsey53=mmse(snew53-x);
mmsey54=mmse(snew54-x);
閾值處方法六
m=40;
cxd6=c;
for j=1:jN
flk = first(j):last(j);
thr1=thselect(s,’heursure‘);
for k=0:(length(flk)-1
)
djk=c(first(j)+k);為了簡化程序
absdjk=abs(djk);
thr2=thr1/3;
if absdjk》thr1
djk=djk’*(absdjk.^m-thr1.^m)/absdjk.^m;
elseif djk
 電子發燒友App
電子發燒友App










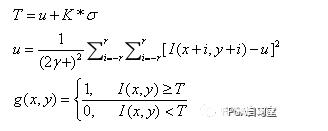
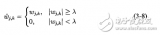















評論