旋轉式位置編碼(RoPE)最早是論文[1]提出的一種能夠將相對位置信息依賴集成到 self-attention 中并提升 transformer 架構性能的位置編碼方式。而目前很火的 LLaMA 模型也是采用該位置編碼方式。
接下來結合代碼和論文來解讀一下 RoPE。
基本概念
首先論文中定義一個長度為 N 的輸入序列為:
其中 wi 表示輸入序列中第 i 個 token,而輸入序列 SN 對應的 embedding 表示為:
其中 xi 表示第 i 個 token wi 對應的 d 維詞嵌入向量。
接著在做 self-attention 之前,會用詞嵌入向量計算 q, k, v 向量同時加入位置信息,函數公式表達如下:
其中 qm 表示第 m 個 token 對應的詞向量 xm 集成位置信息 m 之后的 query 向量。而 kn 和 vn 則表示第 n 個 token 對應的詞向量 xn 集成位置信息 n 之后的 key 和 value 向量。
而基于 transformer 的位置編碼方法都是著重于構造一個合適的 f{q,k,v} 函數形式。
而計算第 m 個詞嵌入向量 xm 對應的 self-attention 輸出結果,就是 qm 和其他 kn 都計算一個 attention score ,然后再將 attention score 乘以對應的 vn 再求和得到輸出向量 om:
絕對位置編碼
對于位置編碼,常規的做法是在計算 query, key 和 value 向量之前,會計算一個位置編碼向量 pi 加到詞嵌入 xi 上,位置編碼向量 pi 同樣也是 d 維向量,然后再乘以對應的變換矩陣 W{q,k,v}:
而經典的位置編碼向量 pi 的計算方式是:
其中 p_{i,2t} 表示位置 d 維度向量 pi 中的第 2t 個元素也就是偶數索引位置的計算公式,而 p_{i,2t+1} 就對應奇數索引位置的計算公式。
python 代碼如下:
#?position?就對應?token?序列中的位置索引?i #?hidden_dim?就對應詞嵌入維度大小?d #?seq_len?表示?token?序列長度 def?get_position_angle_vec(position): ????return?[position?/?np.power(10000,?2?*?(hid_j?//?2)?/?hidden_dim)?for?hid_j?in?range(hidden_dim)] #?position_angle_vecs.shape?=?[seq_len,?hidden_dim] position_angle_vecs?=?np.array([get_position_angle_vec(pos_i)?for?pos_i?in?range(seq_len)]) #?分別計算奇偶索引位置對應的?sin?和?cos?值 position_angle_vecs[:,?0::2]?=?np.sin(position_angle_vecs[:,?0::2])??#?dim?2t position_angle_vecs[:,?1::2]?=?np.cos(position_angle_vecs[:,?1::2])??#?dim?2t+1 #?positional_embeddings.shape?=?[1,?seq_len,?hidden_dim] positional_embeddings?=?torch.FloatTensor(position_angle_vecs).unsqueeze(0)
旋轉式位置編碼
接著論文中提出為了能利用上 token 之間的相對位置信息,假定 query 向量 qm 和 key 向量 kn 之間的內積操作可以被一個函數 g 表示,該函數 g 的輸入是詞嵌入向量 xm , xn 和它們之間的相對位置 m - n:
接下來的目標就是找到一個等價的位置編碼方式,從而使得上述關系成立。
假定現在詞嵌入向量的維度是兩維 d=2,這樣就可以利用上2維度平面上的向量的幾何性質,然后論文中提出了一個滿足上述關系的 f 和 g 的形式如下:
上面的公式一眼看過去感覺很復雜,怎么理解呢?
首先我們得先了解一下基本的復數相關知識。
首先看到上述 f 和 g ?公式中有個指數函數
這個其實是歐拉公式 [2],其中 x 表示任意實數, e 是自然對數的底數,i 是復數中的虛數單位,則根據歐拉公式有:
上述指數函數可以表示為實部為 cosx,虛部為 sinx 的一個復數,歐拉公式 [2] 建立了指數函數、三角函數和復數之間的橋梁。
則上述 f 和 g ?公式中的
然后我們看回公式:
其中 Wq 是個二維矩陣,xm 是個二維向量,相乘的結果也是一個二維向量,這里用 qm 表示:
然后首先將 qm 表示成復數形式:
接著
其實就是兩個復數相乘:
我們首先來復習一下復數乘法的性質:
可以看到,復數乘法也是用的分配律,還有用到了復數的一個性質:
然后就有:
將結果重新表達成實數向量形式就是:
相信讀者看到這里會發現這不就是 query 向量乘以了一個旋轉矩陣[5]嗎?
這就是為什么叫做旋轉式位置編碼的原因。
同理可得 key 向量 kn :
最后還有個函數 g:
其中 Re[x] 表示一個復數 x 的實部部分,而
則表示復數
的共軛,復習一下共軛復數的定義:
所以可得:
繼續可得:
ok,接下來我們就要證明函數 g 的計算公式是成立的。
首先回顧一下 attention 操作, 位置 m 的 query 和位置 n 的 key 會做一個內積操作:
接著繼續之前先復習一下三角函數的一些性質[3]:
好了回到上面那坨式子,我們整理一下:
這就證明上述關系是成立的,位置 m 的 query 和位置 n 的 key 的內積就是函數 g。
然后上面的講解是假定的詞嵌入維度是2維向量,而對于d >= 2 的通用情況,則是將詞嵌入向量元素按照兩兩一組分組,每組應用同樣的旋轉操作且每組的旋轉角度計算方式如下:
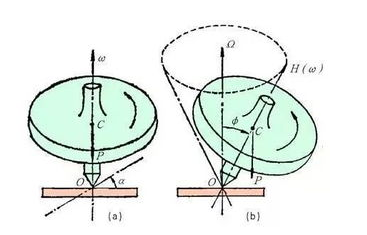
所以簡單來說 RoPE 的 self-attention 操作的流程是,對于 token 序列中的每個詞嵌入向量,首先計算其對應的 query 和 key 向量,然后對每個 token 位置都計算對應的旋轉位置編碼,接著對每個 token 位置的 query 和 key 向量的元素按照 兩兩一組 應用旋轉變換,最后再計算 query 和 key 之間的內積得到 self-attention 的計算結果。
論文中有個很直觀的圖片展示了旋轉變換的過程:
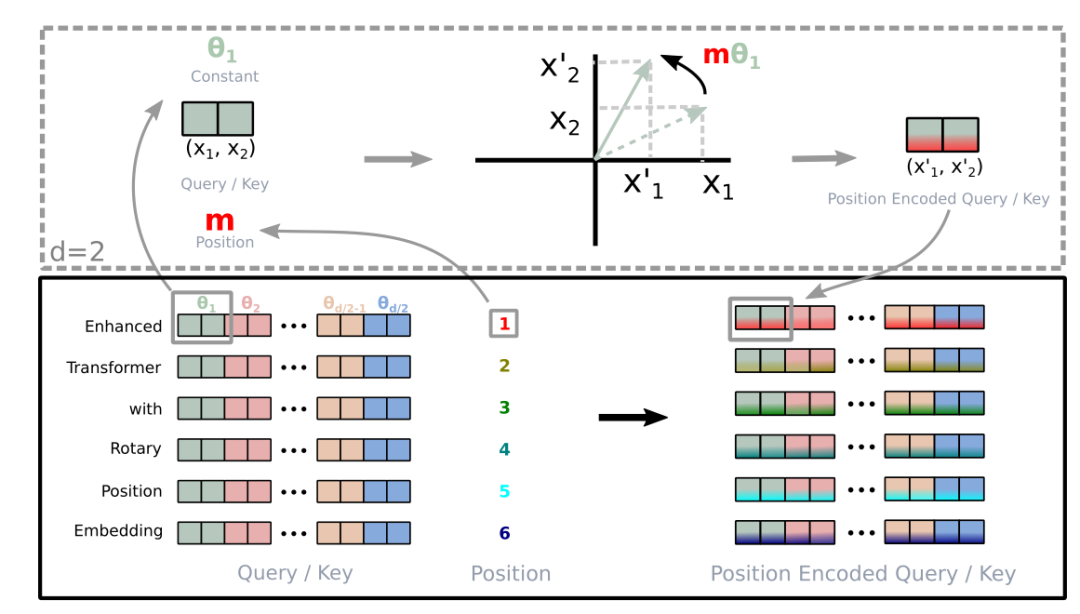
LLaMA 官方實現代碼 [4] 如下(經過簡化):
?
?
def?precompute_freqs_cis(dim:?int,?seq_len:?int,?theta:?float?=?10000.0): ????#?計算詞向量元素兩兩分組之后,每組元素對應的旋轉角度 ????freqs?=?1.0?/?(theta?**?(torch.arange(0,?dim,?2)[:?(dim?//?2)].float()?/?dim)) ????#?生成?token?序列索引?t?=?[0,?1,...,?seq_len-1] ????t?=?torch.arange(seq_len,?device=freqs.device) ????#?freqs.shape?=?[seq_len,?dim?//?2]? ????freqs?=?torch.outer(t,?freqs).float() ????#?torch.polar?的文檔 ????#?https://pytorch.org/docs/stable/generated/torch.polar.html ????#?計算結果是個復數向量 ????#?假設?freqs?=?[x,?y] ????#?則?freqs_cis?=?[cos(x)?+?sin(x)i,?cos(y)?+?sin(y)i] ????freqs_cis?=?torch.polar(torch.ones_like(freqs),?freqs) ????return?freqs_cis def?apply_rotary_emb( ????xq:?torch.Tensor, ????xk:?torch.Tensor, ????freqs_cis:?torch.Tensor, )?->?Tuple[torch.Tensor,?torch.Tensor]: ????#?xq.shape?=?[batch_size,?seq_len,?dim] ????#?xq_.shape?=?[batch_size,?seq_len,?dim?//?2,?2] ????xq_?=?xq.float().reshape(*xq.shape[:-1],?-1,?2) ????xk_?=?xk.float().reshape(*xk.shape[:-1],?-1,?2) ???? ????#?轉為復數域 ????xq_?=?torch.view_as_complex(xq_) ????xk_?=?torch.view_as_complex(xk_) ???? ????#?應用旋轉操作,然后將結果轉回實數域 ????#?xq_out.shape?=?[batch_size,?seq_len,?dim] ????xq_out?=?torch.view_as_real(xq_?*?freqs_cis).flatten(2) ????xk_out?=?torch.view_as_real(xk_?*?freqs_cis).flatten(2) ????return?xq_out.type_as(xq),?xk_out.type_as(xk) class?Attention(nn.Module): ????def?__init__(self,?args:?ModelArgs): ????????super().__init__() ????????self.wq?=?Linear(...) ????????self.wk?=?Linear(...) ????????self.wv?=?Linear(...) ???????? ????????self.freqs_cis?=?precompute_freqs_cis(dim,?max_seq_len?*?2) ????def?forward(self,?x:?torch.Tensor): ????????bsz,?seqlen,?_?=?x.shape ????????xq,?xk,?xv?=?self.wq(x),?self.wk(x),?self.wv(x) ????????xq?=?xq.view(batch_size,?seq_len,?dim) ????????xk?=?xk.view(batch_size,?seq_len,?dim) ????????xv?=?xv.view(batch_size,?seq_len,?dim) ????????#?attention?操作之前,應用旋轉位置編碼 ????????xq,?xk?=?apply_rotary_emb(xq,?xk,?freqs_cis=freqs_cis) ???????? ????????#?scores.shape?=?(batch_size,?seq_len,?seqlen) ????????scores?=?torch.matmul(xq,?xk.transpose(1,?2))?/?math.sqrt(dim) ????????scores?=?F.softmax(scores.float(),?dim=-1) ????????output?=?torch.matmul(scores,?xv)??#?(batch_size,?seq_len,?dim) ??#?......
可以看到 LLaMA 的官方實現代碼和論文 [1] 中的描述是一致的。
編輯:黃飛
?
 電子發燒友App
電子發燒友App






























評論