蝶形運算,2點DFT運算稱為蝶形運算,而整個FFT就是由若干級迭代的蝶形運算組成,而且這種算法采用塬位運算,故只需N個存儲單元2. ∑∑(2)式(2)是FFT基4頻域抽取算法的基本運算單元,一般稱為蝶形運算。
1. 2點DFT運算稱為蝶形運算,而整個FFT就是由若干級迭代的蝶形運算組成,而且這種算法采用塬位運算,故只需N個存儲單元2. ∑∑(2)式(2)是FFT基4頻域抽取算法的基本運算單元,一般稱為蝶形運算。下一步再將X(4m+i),i=0,1,2,3分解成4個N42序列,迭代r次后完成計算,整個算法的復雜度減少為O(Nlog4N)
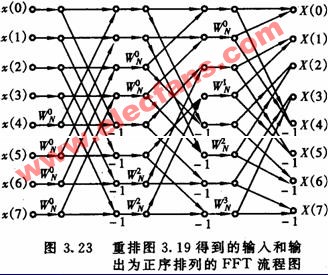
第一列蝶形運算只有一種類型:系數,參加運算的兩個數據點間距為1。第二列有兩種類型的蝶形運算:系數分別為 ,參加蝶形運算的兩個數據點的間距等于2。第叁列有4種類型的蝶形運算:系數分別是 ,參加蝶形運算的兩個數據點的間距等于4。可見,每一列的蝶形類型比前一列增加一倍,參加蝶形運算的兩個數據點的間距也增大一倍,最后一列系數用得最多,為4個,即 ,而前一列只用到它偶序號的那一半,即,
第一列只有一個系數,即。上訴結論可以推廣到N=的一般情況,規律是第一列只有一種類型的蝶形運算,系數是 ,以后每列的蝶形類型,比前一列增加一倍,到第是N/2個蝶形類型,系數是,共N/2個。由后向前每推進一列,則用上述系數中偶數序號的那一半,例如第列的系數則為參加蝶形運算的兩個數據點的間距,則是最末一級最大,其值為N/2,向前每推進一列,間距減少一半。
FFT(快速傅里葉變換)作為數字信號處理領域的核心算法之一。蝶形運算單元是FFT設計的核心單元。本文研究基24FFT蝶形運算單元芯片設計。基于TSMC(***集成電路制造公司)0.18LmCMOS標準單元庫的半定制ASIC(專用集成電路)設計,采用自頂向下、以關鍵模塊為設計對象的設計方法,使用VerilogHDL描述系統,在Modelsim、DesignCompiler和ASTRO等EDA(電子設計自動化)工具中完成
基4FFT蝶形運算單元的設計
蝶形運算單元是FFT處理器的核心單元,蝶形運算單元結構的穩定性和運算的準確性直接影響到FFT處理器的性能。分析基4FFT的特點,綜合考慮面積、性能、功耗各個方面的因素,設計出結合流水線技術和并行結構的蝶形運算單元。
蝶形運算單元結構設計
基24FFT中蝶形運算單元的處理結構見圖
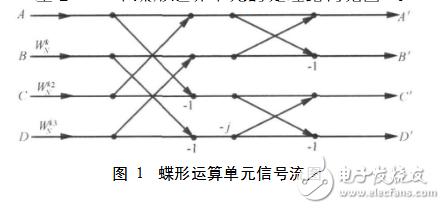
傳統的基4算法是用3個復數乘法器和12個復數加法器構成,每次復數乘法器由4個實數乘法器和2個實數加法實現,每個復數加法由2個實數加法器實現。如此將基24算法的計算結構直接映射至硬件需消耗大量的邏輯資源(12個實數乘法器和22個實數加法器)。
經過重新排列如下:


觀察xc和uc,Xc和Uc,yc和zc,Yc和Zc這4組表達式,可以發現其對應的實部和虛部括號內的內容相同,因此可以將流水線方式與并行結構的思想巧妙結合起來,用4個循環序列對各寄存器進行嚴格的時序控制,只用1個實數乘法器來實現一次復數乘法器,對應3個不同的復數乘法用3個實數乘法并行進行;加法器也并行進行循環使用。因此,完成一個基4FFT蝶形運算單元僅需要3個實數乘法以及6個實數加法,相比傳統基24FFT蝶形運算單元,可節省75%的乘法器邏輯資源和72.7%的加法器邏輯資源。
蝶形運算單元的結構如圖2所示
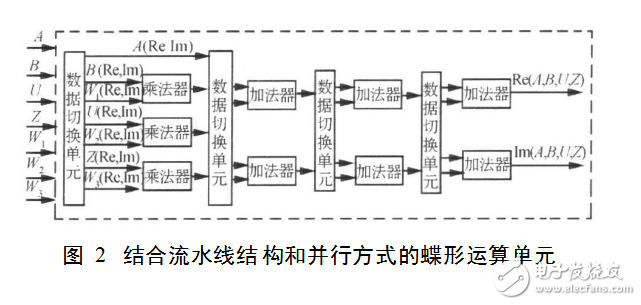
數據切換單元
流水線技術與并行結構相結合的方法可以提高設計的靈活性,減小核心單元的面積,提高芯片運行的速度。流水線技術與并行結構相結合必須在時序的嚴格控制下執行。
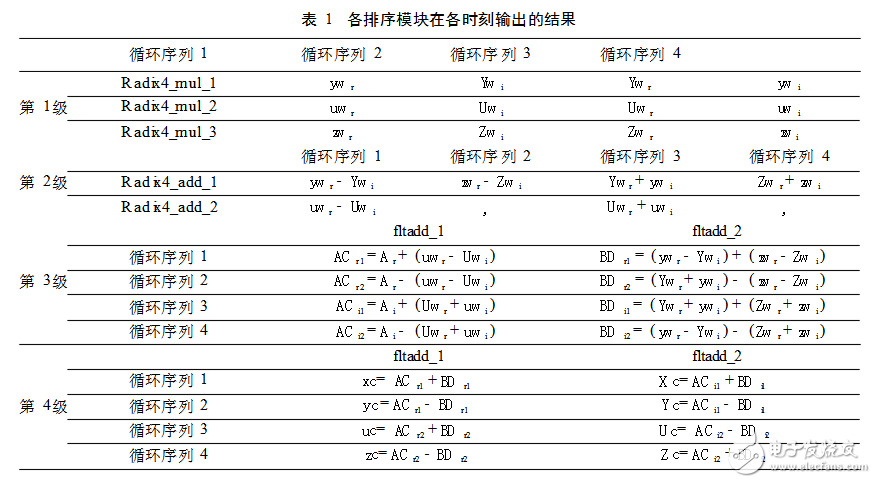
數據切換單元由狀態機組成,以蝶形運算單元的第1級數據切換單元為例。每組數據輸入乘法器分為4個狀態(分別為A、B、C、D)。狀態A輸入乘數的實部和旋轉因子的實部;狀態B輸入乘數的實部和旋轉因子的虛部;狀態C輸入乘數的虛部和旋轉因子的實部;狀態D輸入乘數的虛部和旋轉因子的虛部。其他3級數據切換單元根據前一級運算結構輸出以此類推得到。每一級的具體結果以及步驟見表1。完成4級運算后,并行輸出結果的實部和虛部
浮點乘法器的設計
本設計中浮點數乘法器需完成2個IEEE754單精度浮點數之間的乘法,包括3個部分尾數乘法、指數加法和符號處理。浮點乘法器結構見圖3
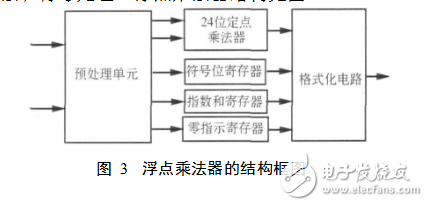
乘法的處理可分為3個步驟:
a)對輸入數據進行預處理,即判斷輸入中是否有0,同時將輸入數據的符號位、指數部分以及尾數部分拆開分別處理,符號位寄存,指數部分相加,尾數部分預處理;
b)將23位尾數和1位隱含位/10構成的24位有效數送入定點乘法器進行運算,并寄存預處理單元的其他輸出數據;
c)接收定點乘法運算結果以及相關寄存器輸出,將最終結果規格化為IEEE754標準單精度浮點格式。
24位定點乘法器采用了經典的陣列式結構結合改進Booth算法的樹形結構。陣列式定點乘法器結構規整,適合于流水線處理,但是流水線深度過深,初始時延過長,硬件資源消耗過大。
改進的Booth算法將24位定點乘法運算的部分積由24個壓縮至13個,降低硬件開銷,減少流水線級數。利用改進的Booth算法設計一種華萊士樹形結構,如圖4所示。

用3級4B2壓縮器將13個部分積逐級壓縮到2個,級間插入寄存器實現全流水,壓縮后的2個部分積用快數加法器相加得到最終結果。4B2壓縮器的邏輯結構見圖5,由4B2壓縮單元級聯組成。
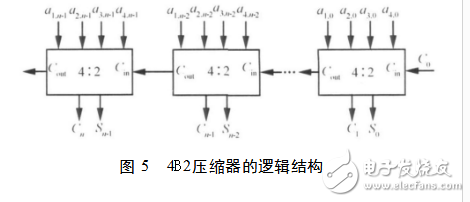
對并行的全加器進行邏輯化簡可以得到4B2壓縮單元,其邏輯表達式如下:
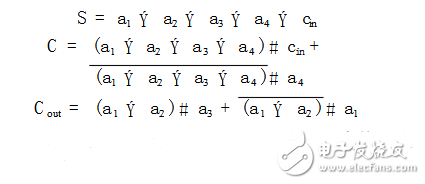
利用改進后的結構設計的定點乘法器流水線深度只有7級,降低了硬件成本,減小了流水線的初始延時,提高了系統的性能。
浮點乘法器的改進
分析4B2壓縮器的邏輯表達式,可以發現當輸入的a1,a2,a3,a4相同的時候,輸出的Cout相同;當輸入的a1,a2,a3,a4以及Cin相同時,輸出的S和C都相同。
再分析Booth算法。Booth編碼是針對有符號數的乘法,需要將符號位擴展并且移位;2個24bit定點數相乘,得到1個48bit的乘積,因此產生的部分積有2bit~24bit不等的相同符號位。
在華萊士樹形結構中,Booth算法得到的13個48bit的部分積相加,只需要將其中的25bit相加,其他23bit可以通過分析直接得到和位和進位。每個乘法器節省了70個4B2壓縮器,減少了關鍵路徑時間,提高了乘法器的執行速度。
浮點加法器設計
浮點加法器包括數據預處理電路、26bit加法器以及浮點數格式化處理,采用流水線技術,見圖6。
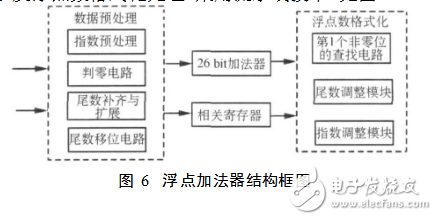
浮點加法的處理步驟如下:
a)數據預處理部分,包括判零電路,如果其中一個加數為0,那么加法輸出結果應該等于另一個加數;指數對齊;尾數移位實現尾數補齊和隱藏位/10擴展以及符號位擴展。
b)運用進位保留和進位傳遞相結合的26bit加法器。
c)將最終結果再格式化為IEEE754標準單精度浮點格式。
26bit定點加法器是浮點加法器的核心加法單元,本設計采用了超前進位和進位保留相結合的方法,見圖7。超前進位加法器的特點是各級進位信號同時產生,大大減少了進位產生的時間,一般不超過4bi,t故將26bit分成6個3bit塊和2個4bit塊。其中,AF_3、AF_4采用超前進位加法器,26bit進位選擇加法器僅用2級流水線就能達到所需性能要求。

浮點加法器的改進
在滿足時序的情況下,分析26bit快速加法器。超前進位加法器適用于不超過4bit的數據,進位保留加法器是以面積換速度。如果采用兩級流水線完成26bit加法器,時序上一定滿足,但是卻以24個AF_3和8個AF_4為代價。基于面積和時序的折衷優化,我們采用以下框圖完成26bit加法器。只需要12個AF_3和4個AF_4即可完成26bit進位選擇加法器。
邏輯綜合
在蝶形運算單元結構完成之后,采用VerilogHDL對整個系統進行了RTL級描述和邏輯綜合及功能驗證。本文基于TSMC0.18LmCMOS標準單元庫,使用Synopsys的DesignCompiler進行邏輯綜合,使用Modsim進行仿真,并且與MATLAB計算結果進行對比。
邏輯綜合
設計目標為200MHz時鐘,設定20%裕量,因此約束時鐘為4ns,具體約束條件如下:時鐘周期4ns,時間抖動和歪斜0.1ns,線負載模型tsmc18_wl120,輸入輸出延時0.8ns,滿足時序的情況下面積最小化。
綜合完成后結果如圖8所示。
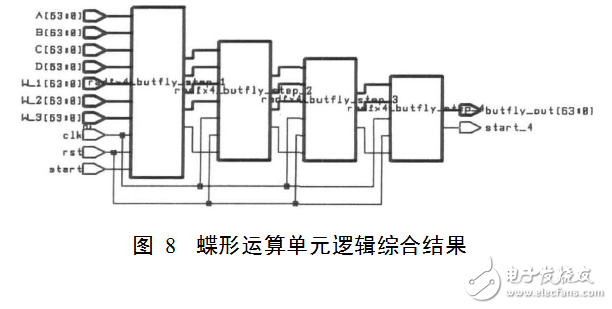
蝶形運算單元邏輯綜合報告顯示關鍵路徑延時3.4ns《4ns,所以slack為正。總單元面積1.12mm2,總的動態功耗為376.9mW。
基24FFT蝶形運算單元使用TSMC0.18LmCMOS標準單元庫,能穩定工作在200MHz的時鐘頻率。采用改進的基24FFT蝶形結構圖,將乘法器節省75%,加法器節省72.7%;采用改進的浮點乘法器和浮點加法器,使蝶形運算單元的面積節省了1.64萬門。
此蝶形運算單元在滿足200MHz的前提下,面積和功耗得到很大改善。對于N點FFT需要log4N級、每級N/4次蝶形運算,假設每級數據需要10點預存,數據輸入輸出需要1024@2個時鐘,完成1024點運算的時間[(1024/4+10)@log41024+1024@2]@5ns=16.89ns。
可見,使用該蝶形運算單元構成FFT處理器在性能上處于領先地位。
 電子發燒友App
電子發燒友App












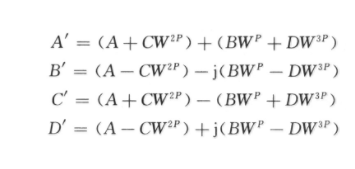
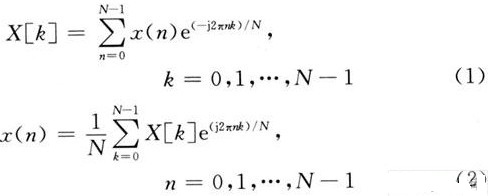










評論