Web文檔聚類中k-means算法的改進
介紹了Web文檔聚類中普遍使用的、基于分割的k-means算法,分析了k-means算法所使用的向量空間模型和基于距離的相似性度量的局限性,從而提出了一種改善向量空間模型以及相似性度量的方法。
關鍵詞: 文檔聚類? k-means算法? 向量空間模型? 相似性度量
Internet的快速發展使得Web上電子文檔資源在幾年間呈爆炸式增長,與數據庫中結構化的信息相比,非結構化的Web文檔信息更加豐富和繁雜。如何充分有效地利用Web上豐富的文檔資源,使用戶能夠快速有效地找到需要的信息已經成為迫切需要解決的問題。
聚類能夠在沒有訓練樣本的條件下自動產生聚類模型。作為數據挖掘的一種重要手段,聚類在Web文檔的信息挖掘中也起著非常重要的作用。文檔聚類是將文檔集合分成若干個簇,要求簇內文檔內容的相似性盡可能大,而簇之間文檔的相似性盡可能小。文檔聚類可以揭示文檔集合的內在結構,發現新的信息,因此廣泛應用于文本挖掘與信息檢索等方面。
文檔聚類算法一般分為分層和分割二種,普遍采用的是基于分割的k-means算法。
k-means算法具有可伸縮性和效率極高的優點,從而被廣泛地應用于大文檔集的處理。針對k-means算法的缺點,許多文獻提出了改進方法,但是這些改進大多以犧牲效率為代價,且只對算法的某一方面進行優化,從而使執行代價很高。
k-means算法中文檔表示模型采用向量空間模型(VSM),其中的詞條權重評價函數用TF*IDF表示。然而實際上這種表示方法只體現了該詞條是否出現以及出現多少次的信息,而沒有考慮對于該詞條在文檔中出現的位置及不同位置對文檔內容的決定程度不同這一情況。另一方面,k-means算法使用基于距離的相似性度量,然而文檔的特征向量一般超過萬維,有時可達到數十萬維,這種高維度使得這種度量方法不再有效。針對以上問題,本文提出相應的解決方法,即改進的k-means算法。實驗表明改進后的k-means算法不僅保留了原算法效率高的優點,而且聚類的平均準確度有了較大提高。
1?k-means算法簡介
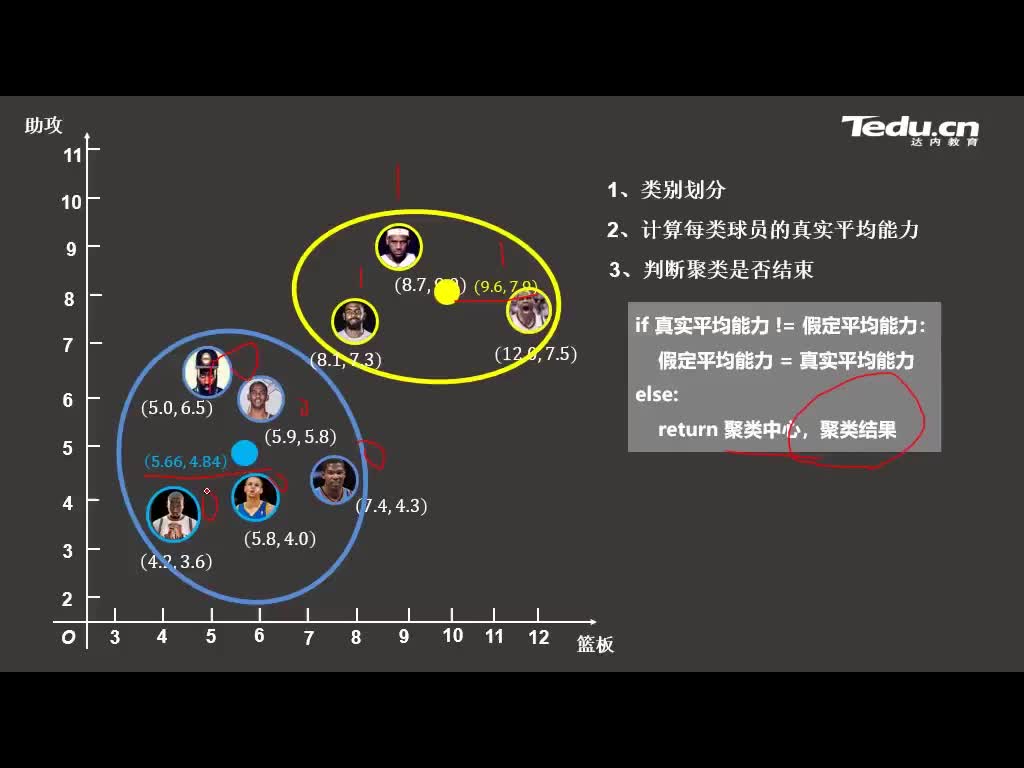
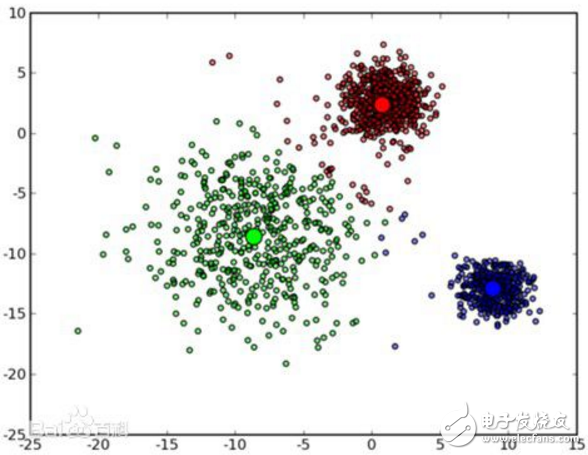
k-means算法是一種基于分割的聚類算法。基于分割的聚類算法可以簡單描述為:對一個對象集合構造一個劃分,形成k個簇,使得評價函數最優。不同的評價函數將產生不同的聚類結果,k-means算法通常使用的評價函數為:

k-means算法的具體過程如下:
(1)選取k個對象作為初始的聚類種子;
(2)根據聚類種子的值,將每個對象重新賦給最相似的簇;
(3)重新計算每個簇中對象的平均值,用此平均值作為新的聚類種子;
(4)重復執行(2)、(3)步,直到各個簇不再發生變化。
k-means算法的復雜度為:O(nkt)。其中:n為對象個數,k為聚類數,t為迭代次數。通常k、t<< n,所以k-means算法具有很高的效率。同時k-means算法具有較強的可伸縮性,除了生成k個聚類外,還生成每個聚類的中心,因此被廣泛應用。
2? k-means算法的分析及其改進
2.1 權重評價函數的改進
k-means算法采用向量空間模型(VSM)將Web文檔分解為由詞條特征構成的向量,利用特征詞條及其權重表示文檔信息。向量d=(ω1,ω2,ω3,∧,ωm)表示文檔d的特征詞條及相應權重。其中:m為文檔集中詞條的數目,ωi(i=1,∧,m)表示詞條ti在文檔d中的權重。特征權重ωi的計算通常采用經典的TF*IDF算法,并進行規格化處理:
??? 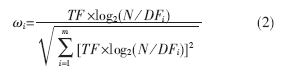
其中:TF表示該詞條ti在文檔d中的頻數,DFi表示文檔集中包含詞條ti的文檔數,N表示文檔集中的文檔數。從公式(2)可以看出,這種特征權重的計算方法是把文檔當做一組無序詞條,詞條特征權重只是體現了該詞條是否出現以及出現次數多少的信息,而對于詞條在文檔中的不同位置對文檔內容的決定程度不同這一問題卻未加考慮。
對于Web文檔而言,由于XML(可擴展標識語言)已經成為Web上新一代數據內容描述標準,因此Web上的文檔聚類應體現XML文檔的特性。XML文檔中的基本單位是元素(element)。元素由起始標簽、元素的文本內容和結束標簽組成。它的語法格式為:
<標簽> 文本內容
基于XML的Web文檔中,用戶把要描述的數據對象放在起始標簽和結束標簽之間,無論文本的內容多長或者多么復雜,XML都可以通過元素的嵌套進行處理。不同標簽下,同一個詞條也可能有不同含義。由此可見,XML文檔中不同位置的詞條對文檔內容的決定程度會有很大的不同。
通常,一個文檔的標題、摘要、關鍵詞以及段首和段尾出現的詞條對整個文檔內容有很大的決定作用。在XML文檔中,通過標簽可以得出詞條對文檔內容的決定程度,但很難對這種決定程度進行準確的定義。因此,本文利用模糊集理論,根據XML文檔特性計算詞條從屬關系系數,并且將其量化為介于0和1之間的隸屬度,加入到原有權重評價函數,從而表明XML文檔具有該詞條特征的程度。
為了簡化計算,詞條在文檔中出現的位置主要分為標題、摘要、關鍵詞、段首尾、特殊標識處和正文幾個部分。其相應權重為σt,在[0,1]之間取值,用lt表示詞條在相應位置出現的次數。加入了詞條隸屬度的權重評價函數為:

2.2 相似性度量的改進
利用向量空間模型處理Web文檔時,由于文檔的繁雜性,表示文檔的特征向量可以達到數萬維,甚至更多。通過預處理階段停用詞和無用高頻詞的過濾后,特征向量的維數雖然顯著減少,但剩余的維數仍然很多。本文實驗中選用的娛樂類1500篇Web文檔在預處理后特征向量的維數仍然達到了8291維。
如此高維的特征向量使得聚類算法的處理時間大大增加,同時對算法的準確性產生不利影響,并且這些特征對于聚類來說大多是無用的,例如聚類算法STC(Suffix Tree Clustering)將特征向量的維數減少到幾十維仍然能夠準確聚類。這主要是因為,對于非結構化的文檔,體現其類別特點的特征詞有很多,當進行某一方面的聚類時,與此無關的特征詞就成了噪音。從這一點來說,文中前面改進的權重評價函數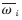 體現了特征詞對文檔內容的貢獻程度,從而突出了與聚類相關的特征詞,降低了無關特征詞的干擾。另一方面,過多的特征詞使得特定的特征詞出現的頻率較低,容易被噪音所淹沒。
體現了特征詞對文檔內容的貢獻程度,從而突出了與聚類相關的特征詞,降低了無關特征詞的干擾。另一方面,過多的特征詞使得特定的特征詞出現的頻率較低,容易被噪音所淹沒。
k-means算法使用基于距離的相似性度量,通過計算文檔向量之間的距離表明文檔之間相似性的大小。通常采用的是余弦函數,計算公式為:

利用向量空間模型對文檔進行聚類只能根據文檔的二種信息:(1)文檔中每個特征詞出現的頻率;(2)文檔的長度。由于文檔長度與文檔所屬的類別之間的關系不大,因此可以把所有的文檔長度進行歸一化處理,從而使文檔向量具有統一的特征維數m。

其中:m為特征向量維數,αk為二個文檔對應特征詞條的四位碼字的十進制數值差的絕對值。由于這種相似性的計算使用的是整數,所以計算速度和精度得到一定的提高。
可以利用簡單的示例驗證公式(5)的合理性。當二個文檔完全相似時,sim(di,dj)的值等于1,而二個文檔完全不同時它的值為0。這種方法不僅反應了文檔之間的差異,而且定量地描述了這種差異性,從而為文檔的聚類提供了依據。下面通過對具體的Web文檔進行實驗并進一步地驗證。
3??實? 驗
實驗用的文檔是從搜狐的中文網站上獲取的娛樂類文檔,選用其中的1500篇。對這1500篇文檔進行手工分類,如表1所示共分為10類。

衡量信息檢索性能的召回率和精度也是衡量分類算法效果的常用指標。然而聚類過程中并不存在自動分類類別與手工分類類別確定的一一對應關系,因此無法像分類一樣直接以精度和召回率作為評價標準。為此本文選擇了平均準確率作為評價的標準。平均準確率通過考察任意二篇文章之間類屬關系是否一致來評價聚類的效果。
試驗中對使用公式(3)和(5)的改進k-means算法和原k-means算法的平均準確度進行了比較,實驗結果如表2所示。
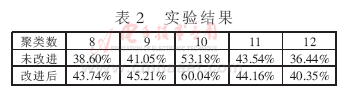
實驗結果表明,改進后的k-means算法與原k-means算法在運行速度上基本相同甚至略快,平均準確度則比原算法有了普遍提高,尤其在正確指定聚類數k時,平均準確度提高了近7%,說明此算法具有較高的準確性。由于實驗中使用的文檔集很小,所以改進的算法優勢不很明顯。
4?結束語
本文對k-means算法進行了改進。根據不同位置的特征詞條對文檔內容的不同決定程度,提出一種新的文檔特征詞條的權重評價函數,并在此基礎上提出一種文檔相似性的度量方法。實驗表明改進后的算法不僅保留了原k-means算法效率高的優點,而且在平均準確度方面比原算法有了較大提高。實驗還表明,k-means算法要依賴原始聚類數k的選擇。如何為初始文檔集選擇合適的聚類數k以及進一步提高平均準確度是今后改進k-means算法的主要研究方向。
參考文獻
1?Fraley C,Raftery A E.How Many Clusters?Which ClusteringMethod?Answers Via Model-Based Cluster Analysis.
Department of Statistics University of Washington Technical Report,1998
2?Xu L.How Many Clustering?:A YING-YANG Machine Based Theory For A Classical Open Problem In Pattern Recognition. IEEE Trans,Neural Networks,1996;3(10)
3?Jiang M F,Tseng S S,Su C M.Two-phase clustering?process for outliers detection.Pattern Recognition Letters,2001;(22)(6~7)
4?Michaud P.Clustering techniques.Future Generation Computer?System,1997;13(6)
5?Pedrycz W,Bagiela A.Granular Clustering:A Granular Signature of Data.IEEE Trans,Neural Networks,2002;32(2)
 電子發燒友App
電子發燒友App































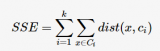










評論