上海交通大學(xué) 蔡 子 編譯自Pedram Roushan. Physics World，2022，(4)：24

本文選自《物理》2022年第5期

由于其迷人的魅力，晶體在過(guò)去幾個(gè)世紀(jì)里一直吸引著我們的注意。人們所熟知的晶體，從雪花到鉆石，通常都是由原子或分子在空間中規(guī)則排列所構(gòu)成的。對(duì)晶體的研究幫助我們建立了一整套框架，可以用于理解其他的空間有序相，例如超導(dǎo)體、液晶和鐵磁相。

周期性振蕩是另外一個(gè)無(wú)處不在的現(xiàn)象。小到原子，大到行星，它可以出現(xiàn)在任何尺寸的系統(tǒng)中。多年來(lái)，我們用它們來(lái)標(biāo)記時(shí)間的流逝，它甚至讓我們思考實(shí)現(xiàn)永動(dòng)機(jī)的可能。空間和時(shí)間上的周期模式的一個(gè)共同特點(diǎn)是他們都降低了系統(tǒng)的對(duì)稱(chēng)性：周期結(jié)構(gòu)明顯破缺了時(shí)間或者空間上的連續(xù)平移對(duì)稱(chēng)性。

在物理學(xué)中，空間與時(shí)間通常具有密切的關(guān)聯(lián)。因此如果一個(gè)多粒子體系能夠顯示出空間上的周期性，那么可以很自然地聯(lián)想到這種周期模式是否能夠自發(fā)地出現(xiàn)在時(shí)間維度。當(dāng)系統(tǒng)的基態(tài)并不滿(mǎn)足系統(tǒng)本身的對(duì)稱(chēng)性時(shí)，意味著系統(tǒng)發(fā)生了自發(fā)對(duì)稱(chēng)破缺。最為常見(jiàn)的例子便是在自然界中廣泛存在的晶體，其連續(xù)平移對(duì)稱(chēng)性被破缺，取而代之的是空間中的離散平移對(duì)稱(chēng)性。

空間周期與時(shí)間周期

在過(guò)去的十年中，物理學(xué)家一直在思考，基態(tài)具有自發(fā)時(shí)間平移對(duì)稱(chēng)性破缺的系統(tǒng)是否能夠存在。空間平移對(duì)稱(chēng)性的破缺似乎與時(shí)間平移對(duì)稱(chēng)性的破缺有著很大的不同。一般來(lái)說(shuō)，空間成序的系統(tǒng)往往由多個(gè)相互作用的粒子組成，而時(shí)間上呈現(xiàn)周期振蕩的系統(tǒng)通常只有很少的幾個(gè)自由度(圖1(a))。事實(shí)上我們一般很難找到多個(gè)相互作用粒子一起周期振蕩的例子。

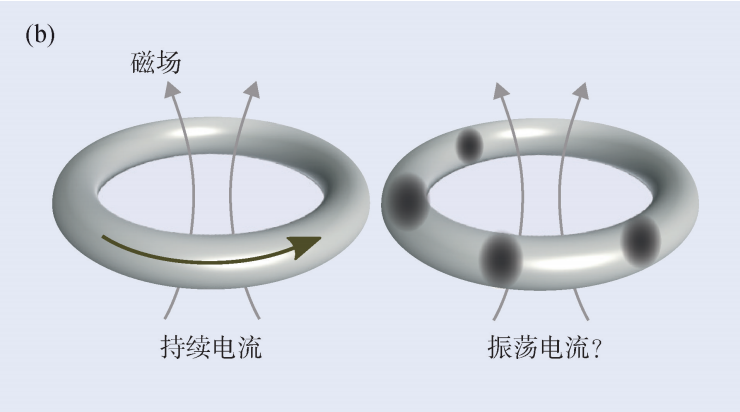
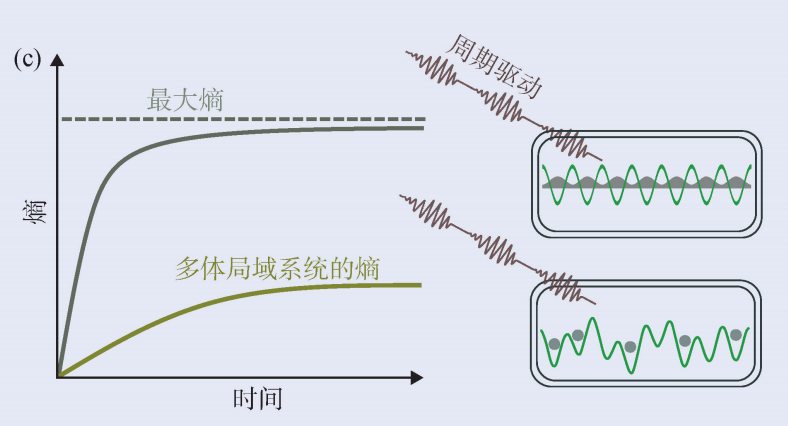
圖1 時(shí)間晶體的挑戰(zhàn)? (a)即使存在一些擾動(dòng)，由相互作用粒子組成的系統(tǒng)所具有的空間周期序依然穩(wěn)定，由此形成了我們所熟知的晶體相。然而時(shí)間周期序通常只對(duì)一個(gè)或幾個(gè)粒子的系統(tǒng)來(lái)說(shuō)是穩(wěn)定的;? (b)當(dāng)磁場(chǎng)穿過(guò)一個(gè)超導(dǎo)環(huán)，會(huì)在環(huán)中產(chǎn)生一個(gè)持續(xù)的電流。維爾切克提出如果粒子間是具有相互作用的，就可能產(chǎn)生一個(gè)振蕩的電流，但是后續(xù)被證明這種振蕩的電流在平衡態(tài)中是不穩(wěn)定的;? (c)熱力學(xué)第二定律指出，一個(gè)大尺寸孤立系統(tǒng)的熵是不會(huì)減少的。通常來(lái)說(shuō)，受到驅(qū)動(dòng)的系統(tǒng)會(huì)通過(guò)從驅(qū)動(dòng)裝置中吸收能量從而達(dá)到熵最大的狀態(tài)。然而在多體局域化系統(tǒng)中，系統(tǒng)的熵則會(huì)穩(wěn)定在一個(gè)較小的值從而允許時(shí)間序的存在

是否可能找到一個(gè)相互作用的可以在無(wú)限長(zhǎng)的時(shí)間內(nèi)持續(xù)振蕩的多體系統(tǒng)？雖然確實(shí)在一些多體系統(tǒng)中可以觀(guān)察到集體同步的振蕩，例如聲子或質(zhì)點(diǎn)彈簧系統(tǒng)，但是這些振蕩在孤立的多體系統(tǒng)中一般無(wú)法持續(xù)。即使能夠持續(xù)，往往需要對(duì)其初始構(gòu)型進(jìn)行高度調(diào)節(jié)，而這種對(duì)初態(tài)的高度依賴(lài)性使其不能構(gòu)成一個(gè)新的物相。

在相互作用多粒子系統(tǒng)中時(shí)空周期性的顯著差異有些出人預(yù)料，畢竟愛(ài)因斯坦的相對(duì)論已經(jīng)將時(shí)間和空間統(tǒng)一成了一個(gè)整體。盡管通過(guò)洛倫茲變換將時(shí)空坐標(biāo)聯(lián)系起來(lái)，卻并不意味著時(shí)空維度的完全等價(jià)，因?yàn)檫€存在著因果律的約束。

面對(duì)熱力學(xué)第二定律

對(duì)于時(shí)間的正向、反向演化，或者對(duì)于一個(gè)給定的方程來(lái)選擇任意的初始時(shí)間，物理基本定律都具有不變性。但熱力學(xué)第二定律則是一個(gè)例外。

熱力學(xué)第二定律告訴我們，任何一個(gè)孤立的多體系統(tǒng)都會(huì)自發(fā)地演化至其平衡態(tài)的構(gòu)型，在此構(gòu)型下我們不能通過(guò)對(duì)局域量的測(cè)量來(lái)分辨時(shí)間的流逝。這種在時(shí)間上具有的同質(zhì)性與我們想要建立一個(gè)穩(wěn)定的時(shí)間序(時(shí)間上的周期結(jié)構(gòu))相矛盾。這種矛盾使得對(duì)時(shí)間晶體的研究極具挑戰(zhàn)性。

在一個(gè)開(kāi)放系統(tǒng)中，系統(tǒng)可以與外界發(fā)生能量交換，封閉系統(tǒng)的熵理論不再適用，因而我們可以通過(guò)調(diào)節(jié)系統(tǒng)的參數(shù)來(lái)建立一個(gè)穩(wěn)定的時(shí)間序。然而在我們的定義中，時(shí)間晶體是一個(gè)孤立相互作用多體系統(tǒng)，其可以在無(wú)限長(zhǎng)的時(shí)間內(nèi)進(jìn)行振蕩。因此系統(tǒng)中大量粒子自由度的存在是這一定義的關(guān)鍵。

舉例來(lái)說(shuō)，在超導(dǎo)體約瑟夫森結(jié)中觀(guān)測(cè)到的振蕩并不構(gòu)成時(shí)間晶體。盡管這些振蕩能夠永久地持續(xù)下去，但是整個(gè)超導(dǎo)體的自由度十分有限：在極低溫下成對(duì)的電子被綁定在一起形成庫(kù)珀對(duì)，進(jìn)而形成一種宏觀(guān)相干態(tài)。其中，不同庫(kù)珀對(duì)的相位自由度都被凍結(jié)，就像當(dāng)我們翻轉(zhuǎn)一個(gè)硬幣時(shí)，其中所有的原子只能跟著一起運(yùn)動(dòng)，而不能各自獨(dú)立運(yùn)動(dòng)。

十年探索

2012年，諾貝爾獎(jiǎng)得主弗蘭克·維爾切克第一次提出了一個(gè)機(jī)制來(lái)實(shí)現(xiàn)一種永久的周期振蕩。他建議用小磁場(chǎng)穿過(guò)一個(gè)超導(dǎo)環(huán)，從而在其中產(chǎn)生一個(gè)無(wú)限期循環(huán)的電流。然而這個(gè)自發(fā)產(chǎn)生的電流雖然是一個(gè)永久的運(yùn)動(dòng)但并不是一個(gè)永久的振蕩，因?yàn)樵诿總€(gè)時(shí)刻，環(huán)上電子密度分布都是均勻且相同的。

維爾切克提出可以在循環(huán)流動(dòng)的庫(kù)珀對(duì)中引入一個(gè)比較弱的相互作用使得它們能夠束縛在一起。這將會(huì)導(dǎo)致在這一系統(tǒng)的基態(tài)中，粒子密度在環(huán)上出現(xiàn)不均勻的分布，而這種空間不均勻的狀態(tài)一旦出現(xiàn)流動(dòng)，會(huì)呈現(xiàn)出一種清晰的振蕩(圖1(b))。然而2014年，物理學(xué)家渡邊悠樹(shù)和押川正毅通過(guò)考慮系統(tǒng)在平衡態(tài)下所需要滿(mǎn)足的一些隱含條件否定了這一結(jié)論。他們更進(jìn)一步提出了“不可行定理”，該定理證明具有非長(zhǎng)程相互作用的系統(tǒng)不可能在其基態(tài)或熱力學(xué)平衡態(tài)下形成時(shí)間晶體。

局域化導(dǎo)致穩(wěn)定

因此為了能夠穩(wěn)定地得到時(shí)間序，不可避免地要跳出平衡態(tài)的限制。一個(gè)最簡(jiǎn)單的解決辦法是通過(guò)將具有周期性的脈沖施加到系統(tǒng)上使其遠(yuǎn)離平衡態(tài)。從表面上看，選擇周期驅(qū)動(dòng)的系統(tǒng)似乎違背直覺(jué)，因?yàn)檫@類(lèi)系統(tǒng)一般會(huì)不斷地從驅(qū)動(dòng)中吸收能量并朝著熵最大的狀態(tài)演化進(jìn)而毀掉所有的序。然而最近的研究表明，如果系統(tǒng)本身具有一個(gè)很強(qiáng)的無(wú)序，則這種無(wú)序能夠避免系統(tǒng)不同能級(jí)之間的能量交換，進(jìn)而防止系統(tǒng)的熵一直增加。滿(mǎn)足這一條件的系統(tǒng)被稱(chēng)為多體局域化系統(tǒng)。

由于熵理論的存在，大多數(shù)系統(tǒng)會(huì)通過(guò)與外部環(huán)境進(jìn)行能量交換抹除對(duì)初始信息的記憶，進(jìn)而達(dá)到熱力學(xué)平衡態(tài)。但是對(duì)于多體局域化的系統(tǒng)來(lái)說(shuō)，無(wú)序結(jié)構(gòu)會(huì)使其無(wú)法達(dá)到熱力學(xué)平衡態(tài)，從而可以無(wú)限期地保留對(duì)初態(tài)信息的記憶。系統(tǒng)的熵最終穩(wěn)定在一個(gè)較小的值，因此可以允許時(shí)間序的存在。

盡管存在周期驅(qū)動(dòng)，能量的凈流動(dòng)卻變?yōu)榱悖氐姆€(wěn)定值會(huì)低于其可能的最大值(圖1(c))。雖然熱力學(xué)第二定律要求一個(gè)孤立系統(tǒng)的熵不會(huì)隨著時(shí)間減少，但熵的飽和值低于其可達(dá)到的最大值并不違背該定律。熱力學(xué)第二定律只要求系統(tǒng)熵的變化率始終不為負(fù)數(shù)，可以為零或其他正值。

借助多體局域化系統(tǒng)的穩(wěn)定性

當(dāng)一個(gè)系統(tǒng)處于平衡態(tài)時(shí)，它不會(huì)再與周?chē)h(huán)境發(fā)生凈的能量流動(dòng)也不會(huì)有新的熵產(chǎn)生。許多理論和實(shí)驗(yàn)的研究表明，多體局域化的系統(tǒng)也會(huì)有這些特性，但是其本質(zhì)卻與平衡態(tài)相差甚遠(yuǎn)。因此它可能是唯一可以產(chǎn)生穩(wěn)定時(shí)間晶體相的系統(tǒng)。迄今為止，所有已知的經(jīng)典系統(tǒng)都沒(méi)有辦法維持無(wú)限期的振蕩。

多體局域化的系統(tǒng)究竟有多穩(wěn)定？我們又能否確定它們不能達(dá)到最大熵的平衡態(tài)呢？事實(shí)上，迄今為止，二維和三維多體局域化系統(tǒng)是否穩(wěn)定依然是一個(gè)有爭(zhēng)議的問(wèn)題。2006年美國(guó)的研究者指出，一維的多體局域化系統(tǒng)能夠在任意級(jí)微擾展開(kāi)下維持它們局域化的性質(zhì)。然而，這并不能排除亞穩(wěn)態(tài)的情況，很有可能只是系統(tǒng)的熱化時(shí)間極長(zhǎng)，才在有限時(shí)間下顯現(xiàn)出局域化的特征。但是2016年，弗吉尼亞大學(xué)的喬治·帕里西在某些特定的系統(tǒng)中，對(duì)幾乎所有非微擾的效應(yīng)進(jìn)行了排除，使得對(duì)多體局域相的研究有了突破性的進(jìn)展。

建立一種新物相

即使我們已經(jīng)觀(guān)測(cè)到時(shí)間序存在的證據(jù)，但是將它稱(chēng)為一個(gè)新的物相需要滿(mǎn)足一定的規(guī)范和要求。我們需要排除目前觀(guān)測(cè)到的證據(jù)只是一個(gè)短時(shí)間行為或者只是一個(gè)在極小參數(shù)范圍內(nèi)精確調(diào)節(jié)結(jié)果的可能性。為了實(shí)現(xiàn)這一目的，我們將考慮以下4個(gè)因素來(lái)測(cè)試時(shí)間響應(yīng)的剛性：(1)為了建立一個(gè)非平衡的物相，我們需要考慮系統(tǒng)在無(wú)限長(zhǎng)時(shí)間這一極限下的情況；(2)在熱力學(xué)中，物相只有在無(wú)限大尺寸的極限下才能被精確定義；(3)證明一個(gè)相具有穩(wěn)定性需要保證它的本征模式對(duì)于施加在其運(yùn)動(dòng)方程上的任何微擾都是穩(wěn)定的；(4)它不具有對(duì)初始構(gòu)型的依賴(lài)性。

通過(guò)使用谷歌的“懸鈴木”量子處理器，我們?cè)谠胍糁谐塘孔佑?jì)算機(jī)上實(shí)現(xiàn)了第一個(gè)令人信服的對(duì)時(shí)間晶體相的觀(guān)測(cè)，并通過(guò)了上述檢驗(yàn)標(biāo)準(zhǔn)。(i)為了探究無(wú)限長(zhǎng)的時(shí)間響應(yīng)并證明觀(guān)測(cè)到的振蕩并不是短暫的，我們?cè)O(shè)計(jì)了一個(gè)時(shí)間反轉(zhuǎn)方案來(lái)區(qū)別內(nèi)在的動(dòng)力學(xué)與外部的退相干(圖2(a))。這使我們能夠從一個(gè)由20個(gè)量子比特組成的鏈中觀(guān)測(cè)到穩(wěn)定的時(shí)間周期序。(ii)為了證明觀(guān)測(cè)到的振蕩能夠存在于更長(zhǎng)的鏈中，我們演示了有限尺寸標(biāo)度，從而能夠確定相變的參數(shù)(圖2(b))。(iii)我們也證明了這種序能夠在一個(gè)很大的參數(shù)范圍內(nèi)被觀(guān)測(cè)到，而且這個(gè)系統(tǒng)的確是局域化的。

最后，(iv)我們利用了“量子典型性”的概念來(lái)表明對(duì)于任何初態(tài)來(lái)說(shuō)都會(huì)存在持續(xù)的振蕩。典型性理論指出從希爾伯特空間中任意挑選出的一個(gè)純態(tài)，對(duì)于該純態(tài)計(jì)算物理量的期待值能夠很好地符合運(yùn)用統(tǒng)計(jì)系綜平均所得到的結(jié)果。因此，利用典型性我們可以規(guī)避從整個(gè)能譜中抽樣所花費(fèi)的指數(shù)級(jí)代價(jià)，并有效地確定所有初態(tài)的響應(yīng)。

圖2 通過(guò)使用由20個(gè)量子比特所組成的鏈，谷歌的量子人工智能團(tuán)隊(duì)驗(yàn)證了實(shí)現(xiàn)穩(wěn)定物相的所有要求? (a)在排除了退相干的影響之后，他們提供了有力的實(shí)驗(yàn)證據(jù)，證實(shí)觀(guān)測(cè)到了一個(gè)穩(wěn)定的而非短暫存在的振蕩，同時(shí)這也是時(shí)間晶體存在的信號(hào);? (b)他們測(cè)試了不同長(zhǎng)度的鏈并指出，時(shí)間晶體序參量在相變之前會(huì)隨著系統(tǒng)尺寸增大而變小，而在相變點(diǎn)之后則相反。對(duì)于這類(lèi)物相的逐步驗(yàn)證是在之前的實(shí)驗(yàn)工作中從未有過(guò)的

實(shí)現(xiàn)一種動(dòng)力學(xué)相

我們通過(guò)一種獨(dú)特的方式在量子處理器上實(shí)現(xiàn)了一個(gè)時(shí)間晶體相。因?yàn)樗械挠?jì)算通常由處理器通過(guò)一系列被稱(chēng)為量子門(mén)的邏輯運(yùn)算來(lái)實(shí)現(xiàn)。這種運(yùn)算和系統(tǒng)本身的動(dòng)力學(xué)并沒(méi)有聯(lián)系，在技術(shù)層面，預(yù)期的哈密頓量并沒(méi)有在處理器上實(shí)現(xiàn)。在這種計(jì)算中，量子處理器的使用方式和經(jīng)典計(jì)算機(jī)是大致相仿的。

然而，這種建立動(dòng)力學(xué)相的方法有著根本的不同。問(wèn)題在于一個(gè)穩(wěn)定的相究竟是否能從一個(gè)含有驅(qū)動(dòng)的多體孤立系統(tǒng)中產(chǎn)生。對(duì)于這類(lèi)問(wèn)題的探索，量子計(jì)算機(jī)是一個(gè)天然的平臺(tái)。但是這一結(jié)果對(duì)于動(dòng)力學(xué)相的完全實(shí)現(xiàn)仍然有一些距離：判斷系統(tǒng)在熱力學(xué)極限下的響應(yīng)依然是一個(gè)巨大的挑戰(zhàn)，因?yàn)橄到y(tǒng)的相干時(shí)間終歸是有限的。這一工作的核心成就便是設(shè)計(jì)了一種實(shí)驗(yàn)方法為下一步的外推提供了基礎(chǔ)。

正如這一結(jié)果中展示的那樣，我們發(fā)展的方案具有一般性并且建立了一種可擴(kuò)展的研究方法，可以被用于在噪聲中程量子計(jì)算機(jī)上研究非平衡物相。

編輯：黃飛

?