摘要: 在許多測距系統中,精確地調整用戶端回復幀的發送時刻是提高測距精度的關鍵。介紹了用FPGA實現的一種數字式成型濾波器組,它可大幅度地縮短發送時刻的調整步長,有效地提高測距精度,已被成功應用于某個測距系統中。
關鍵詞: 測距 幀參考時標 子波形 成型濾波器 成型濾波器組
在許多測距系統中,用戶端接收到基站發送的幀信號后,便以該幀中特定的位置(稱為幀參考時標)為基準發送“回復幀”給基站。基站收到回復幀后,提取它的幀參考時標,并以其作為測距的依據。
?
通常用戶端的系統時鐘精度較低(本文提到的系統時鐘均指用戶端的系統時鐘),因此接收到的幀參考時標會存在誤差。在用戶端經過計算估計出幀參考時標的誤差,再用該誤差調整發送回復幀的時刻,可實現精確測距。因此測距精度取決于兩個因素:幀參考時標誤差的估計精度和回復發送時刻的調整精度。本文主要討論如何提高回復幀發送時刻的調整精度。回復幀是由基帶碼組成的,因此下文中講的發送時刻的高速均指基帶碼發送時刻的調整。
發送時刻的調整精度是由發送時刻的調整步長決定的。在一般的數字系統中,發送時刻的高速步長不小于個系統時鐘的周期。本文利用 Altera 公司的EP20K300EQC240-3型FPGA器件設計了一種成型濾波器組,使發送時刻的調整步長縮短為時鐘周期的五分之一,從而將發送時刻的高速精度大幅度地提高。
1 成型濾波器組調整發送時刻的原理
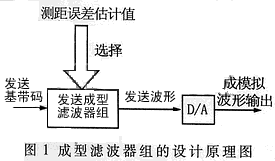
成型濾波器組的設計原理圖如圖1所示。成型濾波器組包括一組成型濾波器。相同的發送基帶碼經成型濾波器組中不同的成型濾波器濾波后,會產生不同延時的發送數據波形。發送數據波形的延時不同,則發送時刻也不同。這就是說,相同的基帶碼經過不同的成型濾波器濾波后可產生不同發送時刻的波形。因此,以測距誤差作為選擇字,根據誤差的大小選擇相應的成型濾波器,就可間接地調整發送基帶碼的時刻。
2 用FPGA設計成型濾波器
通常,系統時鐘頻率遠高于基帶碼的速率,因此在成型濾波前,要在基帶碼的相鄰碼之間進行內插。內插的方式有多種,通常的內插方法是在發送的基帶碼的相鄰碼之間內插“0”。將基帶碼插“0”后,與低通濾波器的沖激響應卷積,再送到D/A轉換器轉換成模擬濾波器就可以實現濾波成型。設計低通濾波器時,為了得到較好的波形,通常采用高階的FIR濾波器。如果在FPGA中用邏輯單元實現高階FIR濾波器,全占用大量的邏輯單元。比如在 Altera 公司的FPGA中用邏輯單元實現一個50階的FIR濾波器,需要26個乘法器和50個加法器,要占用一千多個邏輯單元。而本文利用FPGA中的ROM,用查表的方法設計同樣的FIR濾波器,則只需占用幾十個邏輯單元。圖2是成型濾波器的設計原理圖。該設計包括用數學工具——MATLAB預先設計的部分和在FPGA中實現的部分,MATLAB完成成型濾波后的數據波形文件的設計。FPGA存儲設計好的數據波形文件,并用發送的基帶碼選通相應波形的存儲地址,完成濾波成型。
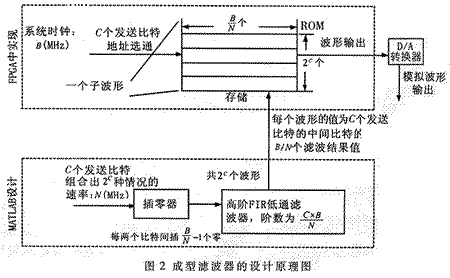
首先用MATLAB設計數據波形文件。設系統基帶碼速率為N MHz,系統時鐘頻率為B MHz。FIR濾波器的階數為(C×B)/N(C為奇數,可根據濾波器的階數要求進行選擇)。FIR濾波器的系數可通過MATLAB進行設計。將C個基帶碼排列組合成2 C種情況。對于每種組合,在C個基帶碼的相鄰碼間內插(B/N)-1個0后,與設計好的濾波器的沖激響應卷積。卷積結果的中間B/N個數據波形值就是該C個基帶組合的中間基帶碼(簡稱中間碼)的濾波結果值。這B/N個數據波形值可以存儲在以該種組合(C個碼)為基地址的ROM中。MATLAB可以計算出所有組合下C個基帶碼的中間碼的濾波結果值。
FPGA將所有濾波結果值存入ROM,將每個濾波結果值所對應的基帶碼組合作為該濾波結果值的存儲地址。系統運行時,用一個C位移位寄存器存儲C個基帶碼,作為地址選通ROM,則ROM輸出的濾波結果值是C個基帶碼的中間碼的濾波結果值。隨著基帶碼依次到達移位寄存器,移位寄存器中C個基帶碼的中間碼也被后面的基帶碼依次替換,ROM輸出的將是依次到達的中間碼的濾波結果值,從而實現基帶碼的濾波成型。
圖2中ROM存儲的數據是設計一個成型濾波器得到的波形數據,為了與下面成型濾波器組的存儲數據相區別,將圖2中ROM存儲的所有波形數據統稱為一個子波形。

3 在FPGA中用成型濾波器組調整發送時刻的方法
圖3是成型濾波器組的實現方案圖。圖中的FPGA的ROM中存儲了E個子波形,稱為一個成型濾波器組。第一個子波形就是圖2所設計的子波形,稱為原來的子波形。之后的E-1個子波形是原來的子波形以時鐘周期的1/E循環左移1,2,…,E-1次得到的。如果得到這些移位后的子波形是設計的關鍵。由于波形的移位在MATLAB中是以數值的變化體現出來的,而通過MATLAB計算可以得到數值精度很高的波形數據,所以用MATLAB設計的波形,移位可以遠小于時鐘周期,因此可以很容易用MATLAB得到以時鐘周期的1/E循環左移后的各個子波形。
各移位后的子波形按循環左移大小依次存儲在ROM中。因此一個時鐘周期的延時被劃分成了E個區間,將測距誤差除以時鐘周期,得到余數R,計算出R落在了E個區間中的哪個。選擇該區間的子波形,將該子波形送到調整步長降到時鐘周期的1/E。實際設計時,在MATLAB中將FIR濾波器的沖激響應以時鐘周期的1/E循環左移,再與插零后的基帶碼卷積,就實現了子波形的循環左移。再通常的系統實時產生的濾波是則系統時鐘控制的,延時不會小于一個時鐘周期,因此其調整精度遠不如用MATLAB設計的成型濾波器組的方法。
上面介紹的是子波形循環左移的方法,也可以將子波形循環右移,道理是一樣的。
4 實例與仿真
4.1 子波形的設計與仿真
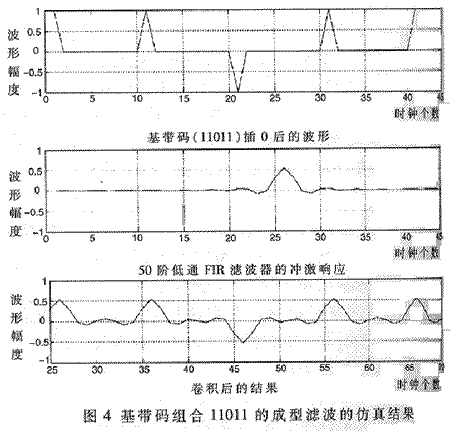
本設計所應用的測距系統的基帶碼速率為2MHz,系統時鐘頻率為20MHz,因此在2MHz基帶碼的相鄰比特間內插20/2-1=9個“0”,然后通過(5×20)/2=50階(C選為5)的FIR濾波器就可實現成型濾波。5個基帶碼可排列成32種組合,圖4是其中的一種基帶碼組合——11011的成型濾波的仿真結果。圖中顯示了該組合插零后與成型濾波器的沖激響應進行卷積的過程。可以看出,卷積的中間10點數據波形正好是插零前5個基帶碼中間的信號0經濾波器平滑后的波形。這10點數據波形存在11011為基地址的ROM中。
4.2 成型濾波器組的設計
由于時鐘周期為50ns,當要求最小調整步長不大于10ns時,在MATLAB中將FIR濾波器的沖激響應以時鐘周期的1/5循環左移,再與插零后的基帶碼進行卷積,就可以得到以時鐘周期的1/5循環左移0,1,2,3,4次后形成的五個子波形。圖5是組合為11011的基帶碼經上述方式產生的五個子波形的圖。
圖5
從圖5中中央的兩條虛線可以看出,經五次移位后的第五個子波形的0碼與原來的子波形的0碼相比,延時為4/5個時鐘周期。這樣就將調整發送時刻的步長減小到時鐘周期的1/5,大幅度提高了測距精度。
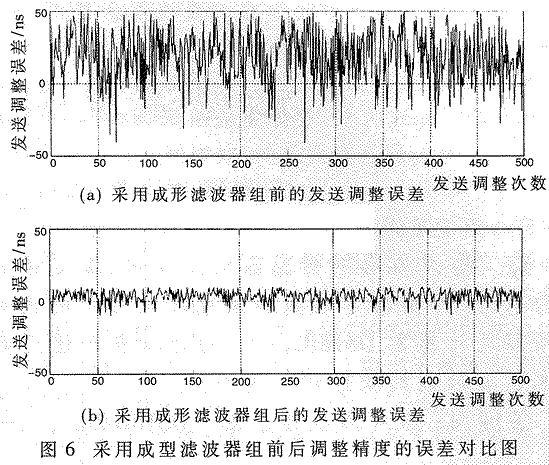
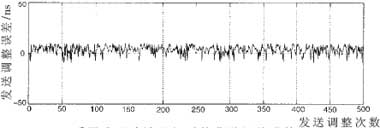
假設估計出的測距誤差是72ns,如果不采用成型濾波器的方法,調整步長為50ns,調整一個時鐘后,會產生72-50=22ns的調整精度誤差。而采用成型濾波器后,調整的步長縮小為10ns,在發送時將第三個數據波形送到D/A轉換器轉換成模擬波形,再將模擬波形送出就可調整精度的誤差降低到72-50-2×10=2ns。圖6是采用成型濾波器組前后調整精度的誤差對比圖(假設測距誤差估計服從高斯分布,均值為25ns,標準差為25ns)。
經圖中的數據計算得出:在不采用成型濾波器組的情況下,發送調整誤差的標準差為18.17ns。采用成型濾波器組后,發送調整誤差的標準為4.42ns,是不采用成型濾波器組時的4.42ns/18.7ns=24.33%。
成型濾波器組占用ROM的數量是則發送時刻調整的精度、成型濾波器的階數、波形的數值量化的比特數、每個基帶碼的時鐘采樣點個數因素決定的。對上面的例子而言,每五個基帶碼組合要生成10個8比特的波形數據,因此所存儲的地址長度為4比特,存儲單位是字節。五個基帶碼共有32種組合,所以一個子波形的地址長度為4+5=9位。在調整步長是時鐘的1/5的要求下,要另加為4+5=9位。在調整步長是時鐘的1/5的要求下,要另加3比特基地址來存儲五個子波形。所以整個成型濾波器組總共消耗的ROM的數量為2(4+5+3)×8=32768比特。
除采用數字電路方式外,許多系統還用模擬電路的方式調整發送時刻:將基帶碼通過模擬觸發電路發送,而測距誤差通過模擬發電路控制基帶碼的發送時刻。這種方式在理論上調整發送時刻的步長更小,但與數字電路相比,易愛到溫度、噪聲等多種因素的影響,可靠性差得多。而本文提出的方法是用數字的方式實現的,穩定性和可靠性均有無可比擬的優越性。
本文設計的成型濾波器充分地利用了硬件中所剩的ROM資源,占用了很少的邏輯單元。用該成型濾波器構成的成型濾波器組,可將基帶碼發送時刻的高速步長減小到時鐘周期的幾分之一,甚至十幾分之一,因此大幅度提高了發送時刻的調整精度。本文的設計已被應用于某個測距系統中,取得了很好的效果。該設計還可應用于其它許多測距系統中,如定位系統、二次雷達等,因此有較高的實用價值。
 電子發燒友App
電子發燒友App




















評論