近日,Mate Labs 聯(lián)合創(chuàng)始人兼 CTO 在 Medium 上撰文《Everything you need to know about Neural Networks》,從神經(jīng)元到 Epoch,扼要介紹了神經(jīng)網(wǎng)絡(luò)的主要核心術(shù)語。
理解什么是人工智能,以及機(jī)器學(xué)習(xí)和深度學(xué)習(xí)如何影響它,是一種不同凡響的體驗(yàn)。在 Mate Labs 我們有一群自學(xué)有成的工程師,希望本文能夠分享一些學(xué)習(xí)的經(jīng)驗(yàn)和捷徑,幫助機(jī)器學(xué)習(xí)入門者理解一些核心術(shù)語的意義。
神經(jīng)元(節(jié)點(diǎn))—神經(jīng)網(wǎng)絡(luò)的基本單元,它包括特定數(shù)量的輸入和一個(gè)偏置值。當(dāng)一個(gè)信號(hào)(值)輸入,它乘以一個(gè)權(quán)重值。如果一個(gè)神經(jīng)元有 4 個(gè)輸入,則有 4 個(gè)可在訓(xùn)練中調(diào)節(jié)的權(quán)重值。

?

?
神經(jīng)網(wǎng)絡(luò)中一個(gè)神經(jīng)元的運(yùn)算

?
連接—它負(fù)責(zé)連接同層或兩層之間的神經(jīng)元,一個(gè)連接總是帶有一個(gè)權(quán)重值。訓(xùn)練的目標(biāo)是更新這一權(quán)重值以降低損失(誤差)。

?
偏置(Offset)—它是神經(jīng)元的額外輸入,值總是 1,并有自己的連接權(quán)重。這確保即使當(dāng)所有輸入為 0 時(shí),神經(jīng)元中也存在一個(gè)激活函數(shù)。
激活函數(shù)(遷移函數(shù))—激活函數(shù)負(fù)責(zé)為神經(jīng)網(wǎng)絡(luò)引入非線性特征。它把值壓縮到一個(gè)更小范圍,即一個(gè) Sigmoid 激活函數(shù)的值區(qū)間為 [0,1]。深度學(xué)習(xí)中有很多激活函數(shù),ReLU、SeLU 、TanH 較 Sigmoid 更為常用。更多激活函數(shù),請(qǐng)參見《一文概覽深度學(xué)習(xí)中的激活函數(shù)》。

?
各種激活函數(shù)

?
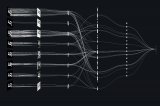
基本的神經(jīng)網(wǎng)絡(luò)設(shè)計(jì)
輸入層—神經(jīng)網(wǎng)絡(luò)的第一層。它接收輸入信號(hào)(值)并將其傳遞至下一層,但不對(duì)輸入信號(hào)(值)執(zhí)行任何運(yùn)算。它沒有自己的權(quán)重值和偏置值。我們的網(wǎng)絡(luò)中有 4 個(gè)輸入信號(hào) x1、x2、x3、x4。
隱藏層—隱藏層的神經(jīng)元(節(jié)點(diǎn))通過不同方式轉(zhuǎn)換輸入數(shù)據(jù)。一個(gè)隱藏層是一個(gè)垂直堆棧的神經(jīng)元集。下面的圖像有 5 個(gè)隱藏層,第 1 個(gè)隱藏層有 4 個(gè)神經(jīng)元(節(jié)點(diǎn)),第 2 個(gè) 5 個(gè)神經(jīng)元,第 3 個(gè) 6 個(gè)神經(jīng)元,第 4 個(gè) 4 個(gè)神經(jīng)元,第 5 個(gè) 3 個(gè)神經(jīng)元。最后一個(gè)隱藏層把值傳遞給輸出層。隱藏層中所有的神經(jīng)元彼此連接,下一層的每個(gè)神經(jīng)元也是同樣情況,從而我們得到一個(gè)全連接的隱藏層。
輸出層—它是神經(jīng)網(wǎng)絡(luò)的最后一層,接收來自最后一個(gè)隱藏層的輸入。通過它我們可以得到合理范圍內(nèi)的理想數(shù)值。該神經(jīng)網(wǎng)絡(luò)的輸出層有 3 個(gè)神經(jīng)元,分別輸出 y1、y2、y3。
輸入形狀—它是我們傳遞到輸入層的輸入矩陣的形狀。我們的神經(jīng)網(wǎng)絡(luò)的輸入層有 4 個(gè)神經(jīng)元,它預(yù)計(jì) 1 個(gè)樣本中的 4 個(gè)值。該網(wǎng)絡(luò)的理想輸入形狀是 (1, 4, 1),如果我們一次饋送它一個(gè)樣本。如果我們饋送 100 個(gè)樣本,輸入形狀將是 (100, 4, 1)。不同的庫預(yù)計(jì)有不同格式的形狀。
權(quán)重(參數(shù))—權(quán)重表征不同單元之間連接的強(qiáng)度。如果從節(jié)點(diǎn) 1 到節(jié)點(diǎn) 2 的權(quán)重有較大量級(jí),即意味著神將元 1 對(duì)神經(jīng)元 2 有較大的影響力。一個(gè)權(quán)重降低了輸入值的重要性。權(quán)重近于 0 意味著改變這一輸入將不會(huì)改變輸出。負(fù)權(quán)重意味著增加這一輸入將會(huì)降低輸出。權(quán)重決定著輸入對(duì)輸出的影響力。

?
前向傳播
前向傳播—它是把輸入值饋送至神經(jīng)網(wǎng)絡(luò)的過程,并獲得一個(gè)我們稱之為預(yù)測值的輸出。有時(shí)我們也把前向傳播稱為推斷。當(dāng)我們饋送輸入值到神經(jīng)網(wǎng)絡(luò)的第一層時(shí),它不執(zhí)行任何運(yùn)算。第二層接收第一層的值,接著執(zhí)行乘法、加法和激活運(yùn)算,然后傳遞至下一層。后續(xù)的層重復(fù)相同過程,最后我們從最后一層獲得輸出值。

反向傳播
反向傳播—前向傳播之后我們得到一個(gè)輸出值,即預(yù)測值。為了計(jì)算誤差我們對(duì)比了帶有真實(shí)輸出值的預(yù)測值。我們使用一個(gè)損失函數(shù)(下文提及)計(jì)算誤差值。接著我們計(jì)算每個(gè)誤差值的導(dǎo)數(shù)和神經(jīng)網(wǎng)絡(luò)的每個(gè)權(quán)重。反向傳播運(yùn)用微分學(xué)中的鏈?zhǔn)椒▌t,在其中我們首先計(jì)算最后一層中每個(gè)誤差值的導(dǎo)數(shù)。我們調(diào)用這些導(dǎo)數(shù)、梯度,并使用這些梯度值計(jì)算倒數(shù)第二層的梯度,并重復(fù)這一過程直到獲得梯度以及每個(gè)權(quán)重。接著我們從權(quán)重值中減去這一梯度值以降低誤差。通過這種方式我們不斷接近局部最小值(即最小損失)。

?
學(xué)習(xí)率—訓(xùn)練神經(jīng)網(wǎng)絡(luò)的時(shí)候通常會(huì)使用梯度下降優(yōu)化權(quán)重。在每一次迭代中使用反向傳播計(jì)算損失函數(shù)對(duì)每一個(gè)權(quán)重的導(dǎo)數(shù),并從當(dāng)前權(quán)重減去導(dǎo)數(shù)和學(xué)習(xí)率的乘積。學(xué)習(xí)率決定了更新權(quán)重(參數(shù))值的快慢。學(xué)習(xí)率應(yīng)該盡可能高而不會(huì)花費(fèi)太多時(shí)間達(dá)到收斂,也應(yīng)該盡可能低從而能找到局部最優(yōu)。

?
精度和召回率
準(zhǔn)確率—測量值對(duì)標(biāo)準(zhǔn)(或已知)值的接近程度。
精度—兩個(gè)測量值之間的接近程度,表示測量的可重復(fù)性或可再現(xiàn)性。
召回率(敏感度)—全部相關(guān)實(shí)例中被恢復(fù)的相關(guān)實(shí)例的比率。

?
Tp 指真正,Tn 指真負(fù),F(xiàn)p 指假正,F(xiàn)n 指假負(fù)。
混淆矩陣—維基百科的解釋是:
機(jī)器學(xué)習(xí)領(lǐng)域和統(tǒng)計(jì)分類問題中,混淆矩陣(也稱為誤差矩陣/error matrix)是一個(gè)算法性能的可視化表格,通常在監(jiān)督學(xué)習(xí)中使用(無監(jiān)督學(xué)習(xí)中混淆矩陣通常稱為匹配矩陣,/matching matrix)。矩陣的每一行表示一個(gè)預(yù)測類,每一列表示一個(gè)真實(shí)類(或相反)。使用真實(shí)的名詞使其易于解讀,能簡單地看出系統(tǒng)對(duì)兩個(gè)類別的混淆程度(即將一個(gè)類別的物體標(biāo)記為另一個(gè))。
?

?
混淆矩陣
收斂—隨著迭代次數(shù)增加,輸出越來越接近具體的值。
正則化—用于克服過擬合問題。正則化過程中通過添加一個(gè) L1(LASSO)或 L2(Ridge)規(guī)范到權(quán)重向量 w(通過給定算法學(xué)習(xí)到的參數(shù))上以「懲罰」損失項(xiàng):
L(損失函數(shù))+λN(w)—這里的λ是正則項(xiàng),N(w)是 L1 或 L2 規(guī)范。
歸一化—數(shù)據(jù)歸一化是將一個(gè)或多個(gè)屬性縮放至 0 到 1 的范圍的過程。當(dāng)不知道數(shù)據(jù)分布或分布不是高斯分布(鐘形曲線)()的時(shí)候,歸一化是很有用的,可加速學(xué)習(xí)過程。
全連接層—一個(gè)層所有的節(jié)點(diǎn)的激活函數(shù)值作為下一層的每個(gè)節(jié)點(diǎn)的輸入,若這對(duì)所有的層都成立,則稱這些層為全連接層。

?
全連接層
損失函數(shù)/代價(jià)函數(shù)—損失函數(shù)計(jì)算單個(gè)訓(xùn)練樣本的誤差,代價(jià)函數(shù)是整個(gè)訓(xùn)練集的損失函數(shù)的平均。
「mse」—平均方差
「binary_crossentropy」—二分類對(duì)數(shù)損失(logloss)
「categorical_crossentropy」—多分類對(duì)數(shù)損失(logloss)
模型優(yōu)化器—優(yōu)化器是一種搜索技術(shù),用于更新模型的權(quán)重。
SGD—隨機(jī)梯度下降,支持動(dòng)量算法。
RMSprop—適應(yīng)性學(xué)習(xí)率優(yōu)化方法,由 Geoff Hinton 提出。
Adam—適應(yīng)性矩估計(jì)(Adam)并同樣使用了適應(yīng)性學(xué)習(xí)率。
性能指標(biāo)—用于測量神經(jīng)網(wǎng)絡(luò)性能的指標(biāo),例如,準(zhǔn)確率、損失、驗(yàn)證準(zhǔn)確率、驗(yàn)證損失、平均絕對(duì)誤差、精度、召回率和 f1 分?jǐn)?shù)等等。
批大小—一次前向/反向傳播中適用的樣本數(shù),批大小越大,占用的內(nèi)存量越大。
訓(xùn)練 epochs—模型在訓(xùn)練數(shù)據(jù)集上重復(fù)訓(xùn)練的總次數(shù)。
一個(gè) epoch = 全部訓(xùn)練實(shí)例的一次前向和一次反向傳播。
 電子發(fā)燒友App
電子發(fā)燒友App
























評(píng)論