機器學習算法的分類是棘手的，有幾種合理的分類，他們可以分為生成/識別，參數/非參數，監督/無監督等。

例如，Scikit-Learn的文檔頁面通過學習機制對算法進行分組。這產生類別如：1，廣義線性模型，2，支持向量機，3，最近鄰居法，4，決策樹，5，神經網絡，等等…

但是，從我們的經驗來看，這并不總是算法分組最為實用的方法。那是因為對于應用機器學習，你通常不會想，“今天我要訓練一個支持向量機！”相反，你心里通常有一個最終目標，如利用它來預測結果或分類觀察。

所以在機器學習中，有一種叫做“沒有免費的午餐”的定理。簡而言之，它的意思就是說沒有任何一種算法可以完美地解決每個問題，這對于監督式學習（即預測性建模）尤其重要。

例如，你不能說神經網絡總是比決策樹好，反之亦然。有很多因素在起作用，比如數據集的大小和結構。因此，您應該為您的問題嘗試許多不同的算法，同時使用數據的“測試集”來評估性能并選擇優勝者。

當然，你嘗試的算法必須適合你的問題，這就是選擇正確的機器學習算法的重要性之所在。打個比方，如果你需要清理你的房子，你可以使用真空吸塵器，掃帚或拖把，但是你不會拿出一把鏟子然后開始挖掘。

因此，我們想要介紹另一種分類算法的方法，即通過機器學習所負責的任務來分類。

機器學習的任務

1.回歸

回歸是一種用于建模和預測連續數值變量的監督學習任務。例如預測房地產價格，股價變動或學生考試分數。

回歸任務的特征是具有數字目標變量的標記數據集。換句話說，對于每個可用于監督算法的觀察結果，您都有一些“基于事實”的數值。

1.1。 （正則化）線性回歸

線性回歸是回歸任務中最常用的算法之一。它最簡單的形式是試圖將一個直的超平面整合到你的數據集中（即當你只有兩個變量的時候，你只能得到一條直線）。正如您可能猜到的那樣，當數據集的變量之間存在線性關系時，它的效果是非常好的。

實際上，簡單的線性回歸經常被正則化的同類算法（LASSO，Ridge和Elastic-Net）所忽略。正則化是一種懲罰大系數的技術，以避免過度擬合，它應該調整其懲罰的力度。

優點：線性回歸可以直觀地理解和解釋，并且可以正則化以避免過度擬合。另外，使用隨機梯度下降的新數據可以很容易地更新線性模型。

缺點：當存在非線性關系時，線性回歸表現不佳。它們本身并不具有足夠的靈活性來捕捉更為復雜的模式，對于添加正確的交互作用項或者多項式來說可能會非常棘手和耗時。

實現：Python/ R

1.2。回歸樹（集成）

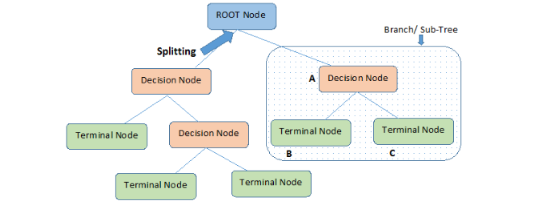
回歸樹（決策樹的一種）是通過將數據集反復分割成單獨的分支來實現分層化學習，從而最大化每個分割信息的增益效果。這種分支結構允許回歸樹自然地學習非線性關系。

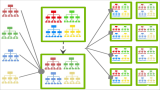
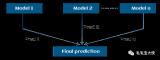
隨機森林（RF）和梯度增強樹（GBM）等集成方法結合了許多單獨樹的特性。我們不會在這里介紹他們的基本機制，但是在實踐中，隨機森林通常表現地非常好，而梯度增強樹則很難調整，但是后者往往會有更高的性能上限。

優點：回歸樹可以學習非線性關系，并且對異常值相當敏銳。在實踐中，回歸樹也表現地非常出色，贏得了許多經典（即非深度學習）的機器學習比賽。

缺點：無約束的單個樹很容易過擬合，因為它們可以保持分支直到它們記住了所有的訓練數據。但是，這個問題可以通過使用集成的方式來緩解。

實現：隨機森林 - Python / R，梯度增強樹 - Python / R

1.3。深度學習

深度學習是指能學習極其復雜模式的多層神經網絡。他們使用輸入和輸出之間的“隱藏層”來模擬其他算法難以學習的數據中介碼。

他們有幾個重要的機制，如卷積和丟棄，使他們能夠有效地從高維數據中學習。然而，與其他算法相比，深度學習仍然需要更多的數據來訓練，因為這些模型需要更多的參數來實現其更準確的推測。

優點：深度學習是在諸如計算機視覺和語音識別等領域內，目前可以被利用的最先進的方法。深度神經網絡在圖像，音頻和文本數據上表現地非常出色，可以輕松地使用成批量的傳播方法來更新數據。它的體系結構（即層的數量和結構）可以適應許多類型的問題，并且它們的隱藏層減少了對特征工程的需要。

缺點：深度學習算法不適合作為通用算法，因為它們需要大量的數據。事實上，對于傳統的機器學習問題，它們的表現通常遜色于決策樹。另外，它們需要密集型的計算訓練，而且需要更多的專業知識來做調試（即設置架構和超參數）。

實現：Python/ R

1.4。特別提及：最近鄰居法

最近鄰居算法是“基于實例的”，這意味著它會保存每個訓練觀察的結果。然后，通過搜索最相似的訓練觀察值并匯集結果，來預測新的觀測值。

這些算法是內存密集型的，對于高維度數據的表現不佳，并且需要有意義的距離函數來計算相似度。在實踐中，訓練正則化回歸或決策樹可能會更節省你的時間。

2.分類

分類是建模和預測分類變量的監督學習任務。例如預測員工的流失，垃圾郵件，財務欺詐或者學生信件等級。

如你所見，許多回歸算法都有分類對應。這種算法適用于預測類（或類概率）而不是實數類。

2.1。 （正則化的）邏輯回歸

邏輯回歸是線性回歸的分類對應。它預測被映射到介于0和1之間的邏輯函數，這意味著預測可以被解釋為類概率。

模型本身仍然是“線性的”，所以當你的類是線性可分的（即它們可以被一個單一的決策表面分開）時候，邏輯回歸算法十分有效。 邏輯回歸也可以通過具有可調懲罰強度的系數來實現正則化。

優點：數據的輸出有一個很好的概率解釋，算法可以正則化以避免過度擬合。 邏輯回歸可以使用隨機梯度下降的方法使得新數據的更新變得更為輕松。

缺點：當存在多個或非線性的決策邊界時，邏輯回歸往往表現不佳。它不夠靈活，無法自然地捕捉到更復雜的關系。

實現：Python/ R

2.2。分類樹（集成）

分類樹是回歸樹的分類對應算法。它們倆被統稱為“決策樹”，或者被稱為“分類和回歸樹（CART）”。

優點：與回歸樹一樣，集成分類樹在實踐中的表現也很好。它們對于異常值的控制是可靠的和可擴展的，并且由于它們的層次結構，能夠自然地對非線性決策邊界進行建模。

缺點：不受約束的單個樹容易過度擬合，但是這可以通過集成方法來緩解。

實現：隨機森林 - Python / R，梯度增強樹 - Python / R

2.3。深度學習

延續其一貫的趨勢，深度學習也很容易適應分類問題。實際上，深度學習往往是分類中比較常用的方法，比如在圖像分類中。

優點：在分類音頻，文本和圖像數據時，深度學習表現地非常出色。

缺點：與回歸一樣，深度神經網絡需要大量的數據進行訓練，所以它不被視為通用算法。

實現：Python的/ R

2.4。支持向量機

支持向量機（SVM）使用稱為核心（kernels）的機制，它計算兩個觀察對象之間的距離。隨后支持向量機算法找到一個決策邊界，最大化不同類別的最近成員之間的距離。

例如，具有線性內核的支持向量機類似于邏輯回歸。因此，在實踐中，支持向量機的好處通常來自于使用非線性的內核來建模一種非線性的決策邊界。

優點：支持向量機可以模擬非線性決策邊界，并有許多內核可供選擇。它們對于過度擬合的控制力也相當強大，特別是在高維空間。

缺點：然而，支持向量機是難以調整的內存密集型算法，而且很依賴于選擇正確的核心，并且不能很好地擴展到較大的數據集里。目前在行業中，隨機森林通常優于支持向量機。

實現：Python/ R

2.5。樸素貝葉斯

樸素貝葉斯（NB）是一個基于條件概率和計數的非常簡單的算法。從本質上講，你的模型實際上是一個概率表，通過你的訓練數據得到更新。為了預測一個新的觀察結果，您只需根據其“特征值”，在“概率表”中查找該類的概率。

它被稱為“樸素的”，是因為它條件獨立的核心假設（即所有輸入特征是相互獨立的），這在現實世界中很少成立。

優點：即使條件獨立性假設很少成立，但樸素貝葉斯模型在實踐中表現得非常出色，特別是它十分簡單。而且很容易實現，并可以和數據集同步擴展。

缺點：由于其簡單化的原因，樸素貝葉斯模型經常被經過適當訓練的其他模型和之前已經列出的算法吊打。

實現：Python/ R

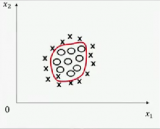
3.聚類

聚類是一種無監督的學習任務，用于基于數據集中的固有結構來發現自然的觀測分組（即聚類）。例子包括客戶細分，電子商務中的類似項目分組以及社交網絡分析。

因為聚類是無監督的（即沒有“正確答案”），所以通常使用可視化的數據來評估結果。如果有“正確的答案”（即你的訓練集中有預標記的聚類），那么選擇分類算法通常更合適。

3.1。K-Means算法

K-Means算法是一種通用算法，它根據點之間的幾何距離（即坐標平面上的距離）進行聚類。這些集群圍繞著質心分組，使它們成為球形，并具有相似的大小。

對于初學者來說，這是我們推薦的一種算法，因為它很簡單，而且足夠靈活，可以為大多數問題獲得合理的結果。

優點：K-Means算法是最流行的聚類算法，因為如果您想預處理數據或者編譯有用的功能，它是一種快速，簡單和擁有令人驚訝的靈活性的一種算法。

缺點：用戶必須指定簇的數目，這并不總是很容易的。另外，如果數據中真實的底層聚類不是球狀的，那么K-Means算法將產生錯誤的聚類。

實現：Python/ R

3.2。近鄰傳播

近鄰傳播是一種相對較新的聚類技術，可以根據點之間的圖距進行聚類。集群傾向于變得更小和具有不均勻的大小。

優點：用戶不需要指定簇的數量（但是需要指定“樣本偏好”和“阻尼”超參數）。

缺點：近鄰傳播的主要缺點是速度很慢，占用內存很大，難以擴展到較大的數據集。另外，它也需要假設真正的底層集群是球狀的。

實現：Python/ R

3.3。分層/凝聚

分層聚類，又名聚集聚類，是基于相同思想的一套算法：（1）從它自己的聚類中的每個點開始。 （2）對于每個簇，根據一些標準將其與另一個簇合并。 （3）重復，直到只剩下一個群集，并留下一個簇的層次結構。

優點：分層聚類的主要優點是不會假設球體是球狀的。另外，它可以很好地擴展到更大的數據集里。

缺點：就像K-Means算法一樣，用戶必須選擇聚類的數量（即在算法完成之后要保留的層次級別）。

實現：Python/ R

3.4。 DBSCAN（Density-Based Spatial Clustering of Applications with Noise）

DBSCAN是一種基于密度的算法，可以為密集的點區域生成集群。還有一個最近的新發展被稱為HDBSCAN，允許產生密度不同的集群。

優點：DBSCAN不假設集群為球狀，其性能也是可擴展的。另外，它不需要將每個點都分配給一個簇，從而減少簇的噪聲（這可能是一個弱點，取決于你的用的地方）。

缺點：用戶必須調用超參數“epsilon”和“min_samples”，它們定義了簇的密度。 DBSCAN對這些超參數非常敏感。

實現：Python/ R