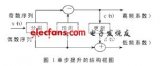
小波變換的原理

　　所謂的小波的小是針對傅里葉波而言，傅里葉波指的是在時域空間無窮震蕩的正弦（或余弦波）。

　　相對而言，小波指的是一種能量在時域非常集中的波，它的能量有限，都集中在某一點附近，而且積分的值為零，這說明它與傅里葉波一樣是正交波。

　　舉一些小波的例子：

　　可以看到，能量集中在x軸0值附近，以y軸的0值為基線，上下兩個區域的波形面積相等。

　　眾所周知，圖像的傅里葉變換是將圖像信號分解為各種不同頻率的正弦波。同樣，小波變換是將圖像信號分解為由原始小波位移和縮放之后的一組小波。

　　小波在圖像處理里被稱為圖像顯微鏡，原因在于它的多分辨率分解能力可以將圖片信息一層一層分解剝離開來。剝離的手段就是通過低通和高通濾波器，

　　這里我們以一個圖像的橫向一維為例，講講小波的分解與還原，采用的是Haar小波做分解：

　　圖像原始像素矩陣：［6 4 8 7 5 9 3 2］

　　分解低通濾波器：［ 1 1］/sqrt（2）

　　分解高通濾波器：［-1 1］/sqrt（2）

　　1、用低通濾波器與原始像素矩陣做卷積得：［8 10 12 15 12 14 12 5］/sqrt（2）

　　下采樣得：［10 15 14 5］/sqrt（2） -----》L

　　2、用高通濾波器與原始像素矩陣做卷積得：［-4 2 -4 1 2 -4 6 1］/sqrt（2）

　　下采樣得：［2 1 -4 1］/sqrt（2） -----》H

　　上例為一維情況，二維情況在做完橫向濾波之后再進行縱向濾波即可。

　　二、逆變換過程：

　　重構低通濾波器：［1 1］/sqrt（2）

　　重構高通濾波器：［1 -1］/sqrt（2）

　　1、對L數組插值得：［0 10 0 15 0 14 0 5］/sqrt（2）

　　再用低通濾波器做卷積得：［10 10 15 15 14 14 5 5］/2

　　2、對H數組插值得：［0 2 0 1 0 -4 0 1］/sqrt（2）

　　再用高通濾波器做卷積得：［2 -2 1 -1 -4 4 1 -1］/2

　　兩個數組求和得：［6 4 8 7 5 9 3 2］ ，矩陣被還原了。

　　三、基于小波變換的圖像壓縮

　　我們知道，圖像的低頻部分保存的是圖像的輪廓信息，而高頻保存的是圖像的邊緣和細節信息，大量的研究表明，幅值低的高頻信息對于圖像共享較小，

　　丟棄對圖像質量的影響不大，所以小波變換的特性給了圖像壓縮一個很好的工具，將原圖進行小波分解以后，為高頻信息設置一個閾值a，假如該點的值小于a則置零這樣就拋棄掉了圖像中影響不大的低幅值高頻信息，還原出來的圖像沒有明顯的質量下降，但是占用空間卻變小了。

　　給一個別人論文里的示例和統計：

　　效果：

　　圖像小波變換的matlab實現詳解

　　1、 一維小波變換的 Matlab 實現

　　（1） dwt 函數

　　功能：一維離散小波變換

　　格式：［cA，cD］=dwt（X，‘wname’）

　　［cA，cD］=dwt（X，Lo_D，Hi_D）

　　說明：［cA，cD］=dwt（X，‘wname’） 使用指定的小波基函數 ‘wname’ 對信號 X 進行分解，cA、cD 分別為近似分量和細節分量；［cA，cD］=dwt（X，Lo_D，Hi_D） 使用指定的濾波器組 Lo_D、Hi_D 對信號進行分解。

　　（2） idwt 函數

　　功能：一維離散小波反變換

　　格式：X=idwt（cA，cD，‘wname’）

　　X=idwt（cA，cD，Lo_R，Hi_R）

　　X=idwt（cA，cD，‘wname’，L）

　　X=idwt（cA，cD，Lo_R，Hi_R，L）

　　說明：X=idwt（cA，cD，‘wname’） 由近似分量 cA 和細節分量 cD 經小波反變換重構原始信號 X 。

　　‘wname’ 為所選的小波函數

　　X=idwt（cA，cD，Lo_R，Hi_R） 用指定的重構濾波器 Lo_R 和 Hi_R 經小波反變換重構原始信號 X 。

　　X=idwt（cA，cD，‘wname’，L） 和 X=idwt（cA，cD，Lo_R，Hi_R，L） 指定返回信號 X 中心附近的 L 個點。

　　2、二維小波變換的 Matlab 實現

　　（1） wcodemat 函數

　　功能：對數據矩陣進行偽彩色編碼

　　格式：Y=wcodemat（X，NB，OPT，ABSOL）

　　Y=wcodemat（X，NB，OPT）

　　Y=wcodemat（X，NB）

　　Y=wcodemat（X）

　　說明：Y=wcodemat（X，NB，OPT，ABSOL） 返回數據矩陣 X 的編碼矩陣 Y ；NB 偽編碼的最大值，即編碼范圍為 0～NB，缺省值 NB＝16；

　　OPT 指定了編碼的方式（缺省值為 ‘mat’），即：

　　OPT＝‘row’ ，按行編碼

　　OPT＝‘col’ ，按列編碼

　　OPT＝‘mat’ ，按整個矩陣編碼

　　ABSOL 是函數的控制參數（缺省值為 ‘1’），即：

　　ABSOL＝0 時，返回編碼矩陣

　　ABSOL＝1 時，返回數據矩陣的絕對值 ABS（X）

　　（2） dwt2 函數

　　功能：二維離散小波變換

　　格式：［cA，cH，cV，cD］=dwt2（X，‘wname’）

　　［cA，cH，cV，cD］=dwt2（X，Lo_D，Hi_D）

　　說明：［cA，cH，cV，cD］=dwt2（X，‘wname’）使用指定的小波基函數 ‘wname’ 對二維信號 X 進行二維離散小波變幻；cA，cH，cV，cD 分別為近似分量、水平細節分量、垂直細節分量和對角細節分量；［cA，cH，cV，cD］=dwt2（X，Lo_D，Hi_D） 使用指定的分解低通和高通濾波器 Lo_D 和 Hi_D 分解信號 X 。

　　（3） wavedec2 函數

　　功能：二維信號的多層小波分解

　　格式：［C，S］=wavedec2（X，N，‘wname’）

　　［C，S］=wavedec2（X，N，Lo_D，Hi_D）

　　說明：［C，S］=wavedec2（X，N，‘wname’） 使用小波基函數 ‘wname’ 對二維信號 X 進行 N 層分解；［C，S］=wavedec2（X，N，Lo_D，Hi_D） 使用指定的分解低通和高通濾波器 Lo_D 和 Hi_D 分解信號 X 。

　　（4） idwt2 函數

　　功能：二維離散小波反變換

　　格式：X=idwt2（cA，cH，cV，cD，‘wname’）

　　X=idwt2（cA，cH，cV，cD，Lo_R，Hi_R）

　　X=idwt2（cA，cH，cV，cD，‘wname’，S）

　　X=idwt2（cA，cH，cV，cD，Lo_R，Hi_R，S）

　　說明：X=idwt2（cA，cH，cV，cD，‘wname’） 由信號小波分解的近似信號 cA 和細節信號 cH、cH、cV、cD 經小波反變換重構原信號 X ；X=idwt2（cA，cH，cV，cD，Lo_R，Hi_R） 使用指定的重構低通和高通濾波器 Lo_R 和 Hi_R 重構原信號 X ；X=idwt2（cA，cH，cV，cD，‘wname’，S） 和 X=idwt2（cA，cH，cV，cD，Lo_R，Hi_R，S） 返回中心附近的 S 個數據點。

　　（5） waverec2 函數

　　說明：二維信號的多層小波重構

　　格式：X=waverec2（C，S，‘wname’）

　　X=waverec2（C，S，Lo_R，Hi_R）

　　說明：X=waverec2（C，S，‘wname’） 由多層二維小波分解的結果 C、S 重構原始信號 X ，‘wname’ 為使用的小波基函數；X=waverec2（C，S，Lo_R，Hi_R） 使用重構低通和高通濾波器 Lo_R 和 Hi_R 重構原信號。

　　圖像處理工具箱1. 圖像和圖像數據

　　缺省情況下，MATLAB將圖像中的數據存儲為雙精度類型（double），64位浮點

　　數，所需存儲量很大；MATLAB還支持另一種類型無符號整型（uint8），即圖像矩

　　陣中每個數據占用1個字節。

　　在使用MATLAB工具箱時，一定要注意函數所要求的參數類型。另外，uint8

　　與double兩種類型數據的值域不同，編程需注意值域轉換。

　　3、圖像處理工具箱所支持的圖像類型

　　3.1、真彩色圖像

　　R、G、B三個分量表示一個像素的顏色。如果要讀取圖像中（100，50）處的像素值，

　　可查看三元數據（100，50，1:3）。

　　真彩色圖像可用雙精度存儲，亮度值范圍是［0，1］；比較符合習慣的存儲方法是用無

　　符號整型存儲，亮度值范圍［0，255］

　　3.2、索引色圖像

　　包含兩個結構，一個是調色板，另一個是圖像數據矩陣。調色板是一個有3列和若干行

　　的色彩映象矩陣，矩陣每行代表一種顏色，3列分別代表紅、綠、藍色強度的雙精度數。

　　注意：MATLAB中調色板色彩強度［0，1］，0代表最暗，1代表最亮。