什么是電磁學?
電磁學屬于工程領域,傳統上來說,人們是通過分屬于眾多子領域(例如靜電學或光學)的專業術語和設備來逐漸了解電磁學的。靜電設置中使用的設備(如電容器)和光學器件(如光纖)幾乎沒有共同之處,盡管它們的特性有很大的差異,但所有這些應用基本上都用麥克斯韋方程組進行描述。在工程應用中,這些方程幾乎總是需要使用其他定律作為補充,通過這些定律來描述電磁場與介質相互作用的方式。下表列出了麥克斯韋方程組的微分形式:

我們將在以下各個章節中介紹這些方程的含義。在實際應用中,我們很少需要考慮可能發生的所有電磁現象。相反,我們往往是通過分析各種特殊情況來獲取對電磁學更實際的理解,其中包括靜電、恒定電流、靜磁、準靜態交流電、電感現象、微波工程和光學。
靜電學
靜電學是電磁學的一個子領域,研究靜(非運動)電荷引起的電場。靜電學是麥克斯韋方程組的近似表述,只能用于描述完全以介電常數(有時稱為電容率)表征的絕緣材料或電介質材料。在執行靜電分析時,我們首先從分析中去除所有導電材料(通常是金屬),然后從電介質材料的角度將金屬表面視為外部邊界。靜電分析的典型輸入和輸出匯總如下:
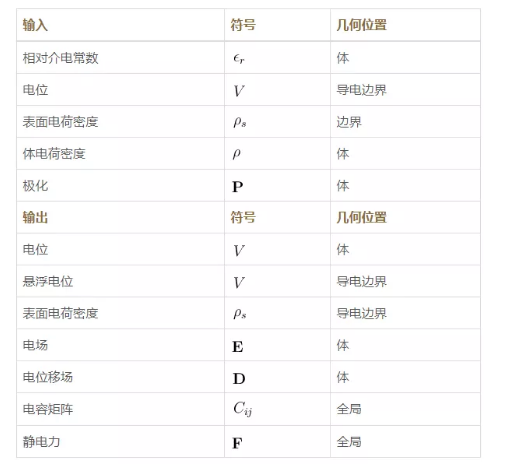
請注意,在靜電分析中,我們將所有電荷都視為靜止,因此沒有電流輸入或輸出。在某些情況下,體電荷密度也可以作為分析的輸出。
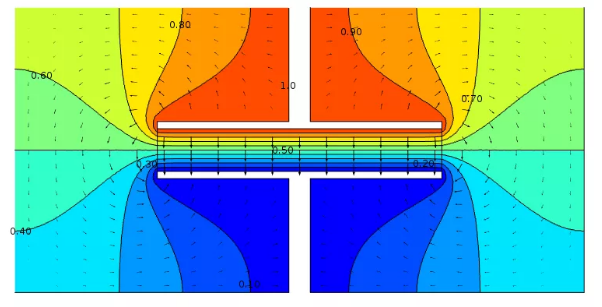
平行板電容器周圍整個體的電位和電場橫截面視圖。圖中用填充等值線表示電位,并通過標簽表明電位水平。電場顯示為具有對數比例的箭頭。電位還受到遠處周圍介質的影響(圖中未顯示)。
靜電分析的典型應用是電容器件和傳感器(如觸摸屏)的電容計算,以及絕緣體、MEMS 加速度計和 MEMS 陀螺儀的介電強度計算。
恒定電流
恒定電流分析用于計算金屬等高導電材料中的恒定電流流動。電子流在電位差的驅動下流過導體,盡管實際上電子的運動方向與電流方向相反,但按照慣例以及由于歷史原因,我們通常認為電流是從高電位流向低電位。這一慣例起源于人們發現電子之前。恒定電流分析中的材料完全用電導率來表征。在執行恒定電流分析時,我們首先從分析中去除所有絕緣材料,然后從導電材料的角度將絕緣表面視為外部邊界。恒定電流分析的典型輸入和輸出匯總如下:

螺旋電感中的電流密度,其中左右邊界之間施加了電位差。圖中顯示電感器內部的電流密度大小值。藍色和紅色分別表示大小的谷值和峰值。箭頭顯示電流密度的方向。電流趨向于流經最短路徑,如該結構內角處的紅色區域所示。
恒定電流分析的典型應用包括電子元件、電纜、高壓系統組件、醫療設備、傳感器、巖土分析和腐蝕。
電準靜態
電準靜態分析是在磁效應可以忽略的情況下,對靜電和恒定電流的泛化分析。如果存在時變場,我們就只能將靜電的電容效應與恒定電流分析的導電效應結合起來分析。對于靜態情況,我們可以將麥克斯韋方程組分為靜電和恒定電流兩種情況,由于二者表示相互排斥的現象,因此必須選擇其一。然而,如果某個物理量隨時間變化,如邊界上的電壓,則總電流為傳導電流與位移電流之和。傳導電流密度與電導率相關,位移電流密度與介電常數相關。電準靜態可以看作是恒定電流方程(包含位移電流產生的額外貢獻)的動態形式。對于驅動電流或電壓呈正弦變化的時諧分析,場變為復值,其中相角表示傳導電流與位移電流之比。
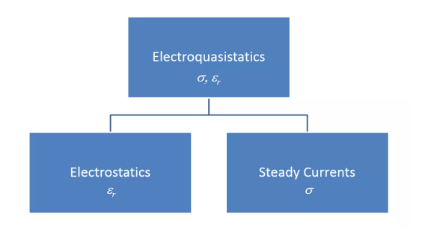
電準靜態是在磁效應可以忽略的情況下,對時變場的靜電和恒定電流的泛化表示。電準靜態分析的典型輸入和輸出匯總如下:

四極質譜儀中的離子軌跡。這種類型的質譜儀利用靜電位和時諧電位的巧妙組合對粒子進行分類。通過調節諧波頻率(本例為 4 MHz)以及靜電場和諧波場的強度,只有一定質量的粒子能通過該設備進行傳輸。電準靜態分析的典型應用包括醫療設備、傳感器,巖土分析和質譜儀。
靜磁學
靜磁學可以看作是恒定電流在磁場中的泛化表示,當我們想要了解導體周圍的磁場信息時,就需要研究這一領域。這種情況下,恒定電流分析有時用作預處理步驟,產生的電流用作后續靜磁分析的輸入。例如,電磁體的分析就是這種情況。用于執行靜磁分析的基本材料屬性是相對磁導率。非線性靜磁分析可能需要更廣泛的材料關系,比如磁場與磁通密度之間的函數關系:B-H 曲線。在許多情況下,靜磁分析的最終目的是計算線圈系統的互感和自感,或磁性元件系統中的力和力矩。永磁體分析是靜磁分析中的一種重要的特殊情況。在這種情況下,磁場的源是永磁化,而非電流。對于這類情況,磁通強度和方向以及力是非常重要的分析結果。
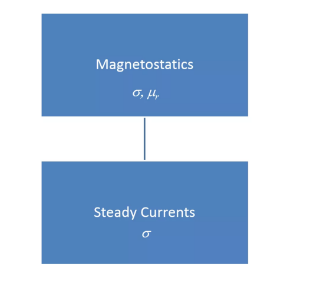
靜磁學可以看作是恒定電流的泛化表示,當我們想要了解磁場信息時,就需要研究這一領域。靜磁分析的典型輸入和輸出匯總如下:

載有恒定電流的電感器周圍的磁通量線。
馬蹄形磁鐵和鐵棒組成的系統中的磁通量可視化效果。
靜磁分析的典型應用包括電磁體、永磁體、線圈、電感器和螺線管。
磁準靜態
我們可以根據麥克斯韋方程組得到一個推論,即電流和電荷隨時間的變化與電磁場的變化不同步。場的變化總是滯后于源的變化,反映了電磁波的傳播速度有限。我們假設這一效應可以忽略不計,通過分析“每個瞬間的穩定電流”,就可以得到電磁場。只要時間變化足夠小,并且研究的幾何結構遠小于波長,就可以使用這種低頻近似。根據經驗,當設備的特征尺寸(電尺寸)小于波長的 10% 時,我們就可以使用準靜態近似。
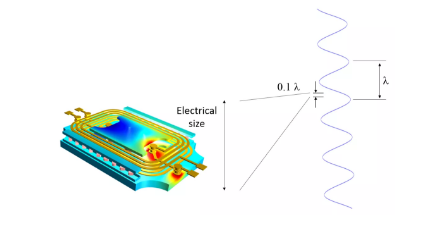
磁準靜態近似對于理解 50 Hz 或 60 Hz 電網中的電磁部件非常重要。這類分析對于更高頻的情況同樣起著非常重要的作用,有時還可與全波電磁分析相結合,用于評估電磁干擾現象。在分析線性材料屬性以及正弦電流和正弦場時,我們采用時諧研究。這類研究每次可以分析部件在一個頻率下的情況,并能夠一次性捕獲部件在所有時間的完整特性,因此非常高效。對于具有非線性材料或波形扭曲的部件,需要進行全瞬態分析,耗費的計算時間較長。磁準靜態元件的激勵通過在所研究域的邊界上施加時變電壓或電流來實現,也可以通過施加體積線圈電流實現。此類激勵方法僅在低頻工況下有效。在頻率較高時,有限光速引起的輻射損耗和影響變得非常重要,此時可能需要進行高頻分析。磁準靜態分析的典型輸入和輸出匯總如下:

纏繞鐵磁芯的 50 Hz 交流線圈。磁準靜態的典型應用包括電纜、電力線、變壓器、發電機、電動機、電抗鎮流器、電感器和電容器。
電磁波
詹姆斯·克拉克·麥克斯韋通過在安培定律中添加一個位移電流項以擴大其適用性,發現了現在稱為麥克斯韋-安培定律的方程。通過將該定律與法拉第定律相結合,他發現了可以用電磁波方程表示的電磁現象的波動性。電磁波方程有多種公式,以下是一個電場相關的公式例子:

用于分析電磁現象的連續介質方法已經證實在許多應用中獲得了成功,但仍存在一定的局限性。在微觀結構中,物質的離散性質起著重要的作用,在分析這種結構時,我們需要采用量子力學方法。對于甚高頻,可以更有效地將電磁波作為射線進行分析;對于高于甚高頻的情況,在模擬單個光子時,還必須為它們與物質之間的電離作用進行建模。為了確定合適的電磁分析方法,我們必須考慮物體特征尺寸與波長之間的相對關系。下圖對這一關系進行了概述。
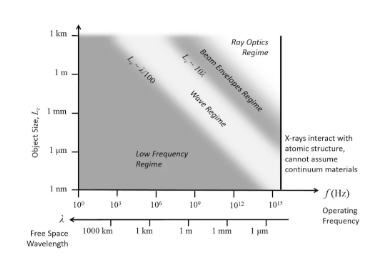
圖中演示了物體相對于波長的大小,以及首選的分析方法。在分析用于引導或輻射電磁波的裝置時,電磁場的波動性是非常重要的因素。這類裝置包括同軸電纜、微波電路、波導和天線等。在高頻下,有限光速的影響變得至關重要,電壓等物理量在邊界段上不再恒定,因此不能直接用于激勵裝置。此時,我們改為在端口或端口邊界上使用場模式,這是與麥克斯韋方程組相容的特征模態。只要使用正確,這些類型的邊界條件就能夠在很少的損耗下激勵結構,從而在理想條件下捕捉結構的固有性能。有時,使用工程方法會非常方便,這種方法用電壓和電流激勵表示來自相鄰電路的饋電。這些激勵可以同一些周密的方案結合使用,從而轉換為兼容的端口激勵。在這種情況下,能量損耗不可避免,這些損耗可能表示實際的設備饋電損耗或人工建模損耗,或兩者兼有。類似地,監聽端口用來以一種與麥克斯韋方程組一致的方式傳輸出射能量。傳輸和反射的能量作為散射參數或 S 參數進行計算,這些參數表示通過各個端口的能量輸入和輸出。電磁波分析的典型輸入和輸出匯總如下:
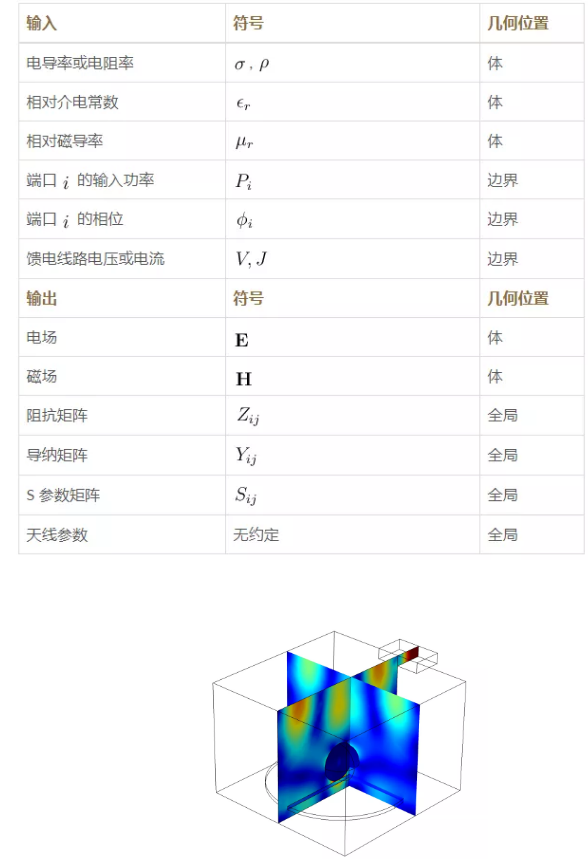
家用微波爐中的電磁駐波。
 電子發燒友App
電子發燒友App









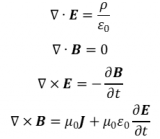






































評論