魚雷流體動力的主向量和力矩
魚雷流體動力
在任何情況下,流體對魚雷的作用力總是以某種規(guī)律連續(xù)分布于魚雷表面的表面力。當(dāng)然,這種分布規(guī)律是取決于許多因素的。
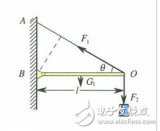
如圖2-6所示,魚雷表面上任一點(diǎn)處單位面積上流體的作用力可以分解為兩個(gè)分量;與表面垂直的分量![]() (稱為壓力);與表面相切的分量(稱為摩擦應(yīng)力)。
(稱為壓力);與表面相切的分量(稱為摩擦應(yīng)力)。
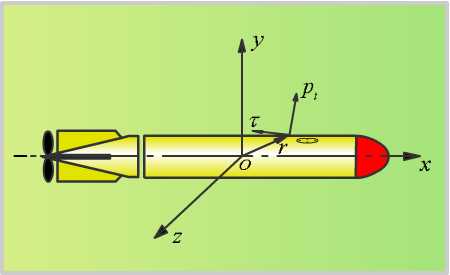
圖2-6魚雷表面受作用力
|
將這一表面力系簡化至原點(diǎn),可得流體動力的主向量和主矩為
|
式中 ——魚雷表面任一點(diǎn)的向徑;
![]() ——魚雷的沾濕面積。
——魚雷的沾濕面積。
容易理解,壓力![]() 是由兩部分組成的,即有
是由兩部分組成的,即有
|
|
(2-3) |
式中 ![]() ——靜水壓力;
——靜水壓力;
![]() ——流體動力壓力。
——流體動力壓力。
這樣,我們便有
|
|
(2-4) | |
|
|
(2-5) | |
| 或?qū)懗?/td> |
|
(2-6) |
|
|
(2-7) | |
| 式中 |
|
(2-8) |
|
|
(2-9) | |
為由靜水壓力所形成的主向量和主矩。顯然,它們正是魚雷的浮力和浮力的主矩。
|
|
(2-10) |
|
|
(2-11) |
為流體動力壓力和摩擦應(yīng)力所形成的主向量和主矩。這部分主向量和主矩正是我們所要研究的對象。
將R和M寫成速度坐標(biāo)系內(nèi)的投影形式:
|
|
(2-12) |
|
|
(2-13) |
式中![]() ——依次為沿x軸,y軸和z軸的單位向量;
——依次為沿x軸,y軸和z軸的單位向量;
![]() —阻力;
—阻力;
![]() —升力;
—升力;
![]() —側(cè)力;
—側(cè)力;
![]() —橫傾力矩;
—橫傾力矩;
![]() —偏航力矩;
—偏航力矩;
![]() —俯仰力矩。
—俯仰力矩。
同樣,還可以寫出R和M在雷體坐標(biāo)系內(nèi)的投影形式:
|
|
(2-14) |
|
? |
(2-15)
? |
式中![]() 稱為縱向力,
稱為縱向力,![]() 稱為法向力,
稱為法向力,![]() 稱為側(cè)向力;
稱為側(cè)向力;![]() 和
和![]() 依次與
依次與![]() 和
和![]() 同名。
同名。
實(shí)驗(yàn)和理論均可證明,在既定流體介質(zhì)(水或空氣)及介質(zhì)溫度的條件下,魚雷的流體動力及力矩與魚雷的流體動力外形,姿態(tài)(攻角及側(cè)滑角![]() )和魚雷的運(yùn)動參數(shù)(速度、角速度,加速度及角加速度)等因素有關(guān)。由此,對既定魚雷以法向力和俯仰力矩為例,可以寫出
)和魚雷的運(yùn)動參數(shù)(速度、角速度,加速度及角加速度)等因素有關(guān)。由此,對既定魚雷以法向力和俯仰力矩為例,可以寫出
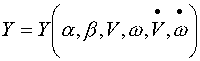 |
(2-16) |
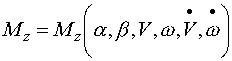 |
(2-17) |
在一般情況下,魚雷的角速度,加速度及角加速度均比較小,我們可以利用泰勒級數(shù)展開的方法,將上述法向力和俯仰力矩寫成如下線性關(guān)系式:
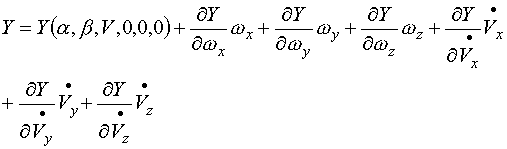 |
(2-18) |
? |
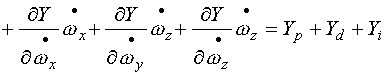 | ||
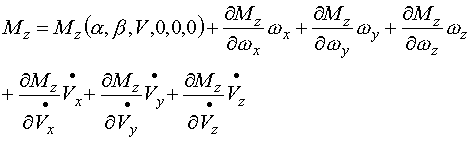 |
(2-19) |
? |
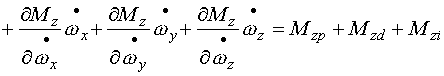 |
以上各導(dǎo)數(shù)均在![]() 出取值。
出取值。
| 在式中 |
|
(2-20) |
|
|
(2-21) |
為魚雷以姿態(tài)角和![]() ,速度V做定常直線平移運(yùn)動時(shí)的法向力和俯仰力矩。它們是該流體動力的主要成分,分別稱為位置力和位置力矩
,速度V做定常直線平移運(yùn)動時(shí)的法向力和俯仰力矩。它們是該流體動力的主要成分,分別稱為位置力和位置力矩
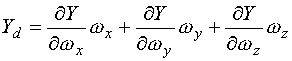 |
(2-22) |
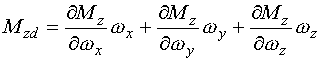 |
(2-23) |
為魚雷由于旋轉(zhuǎn)運(yùn)動而引起的流體動力分量的增量,分別稱為阻尼力和阻尼力矩。
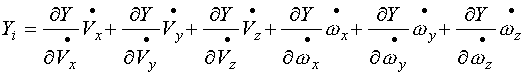 |
(2-24) |
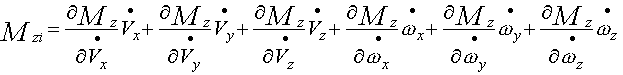 |
(2-25) |
| ? | ? |
為魚雷由于其運(yùn)動的不定常性而引起的流體動力分量的增量,稱為非定常流體動力和力矩。
式(2-24)-(2-25)中的各個(gè)導(dǎo)數(shù),按其自變量的性質(zhì)分別稱為某一流體動力分量對于該自變量的旋轉(zhuǎn)導(dǎo)數(shù),加速度導(dǎo)數(shù)或角加速度導(dǎo)數(shù)。例如:![]() 稱為法向力對于
稱為法向力對于 ![]() 的旋轉(zhuǎn)導(dǎo)數(shù);
的旋轉(zhuǎn)導(dǎo)數(shù);![]() 稱為俯仰力矩對于
稱為俯仰力矩對于![]() 的加速度導(dǎo)數(shù);
的加速度導(dǎo)數(shù);![]() 稱為法向力對于
稱為法向力對于![]() 的角加速度導(dǎo)數(shù)。
的角加速度導(dǎo)數(shù)。
以上,我們僅以法向力Y和俯仰力矩 為例得出上述表達(dá)式。對于其他流體動力分量,也可以得到類似的表達(dá)式。這樣,我們共有6個(gè)位置力分量,18個(gè)旋轉(zhuǎn)導(dǎo)數(shù),18個(gè)加速度導(dǎo)數(shù)和18個(gè)角加速度導(dǎo)數(shù)。上述各量的確定,便最終的確定了魚雷的流體動力和力矩。
 電子發(fā)燒友App
電子發(fā)燒友App
























評論