本文以線性伺服電機的用例說明了比例積分微分 (PID) 控制,包括其背后的數學原理。
通過本文你將能了解到:
PI
D 控制的基礎知識。
電
路中連接元件以完成位置控制的 PID 功能的那些部分的注意事項。
固件
代碼實現。
比例積分微分 (PID) 控制是用于調節系統動態行為的常用方法。在許多工業設備中都可以找到示例,其中它用于控制溫度、壓力、流量、速度或位置等。 PID 控制背后的理論和數學一直是很多討論的主題。但是如何應用這些數學和理論來實現一個真實的設備呢?為了演示這是如何完成的,本文將探討一個完整的示例。
位置控制的任務將針對線性伺服電機的情況進行討論。首先,介紹控制 PID 控制器運行的數學函數。我們將展示函數的各個部分如何在實際設計中組合在一起。具體來說,我們將解決電路中接口元件的注意事項,以完成用于位置控制的 PID 功能的那些部分,以及在將執行控制的微控制器的固件代碼中實現該功能所涉及的內容。
PID 基礎知識
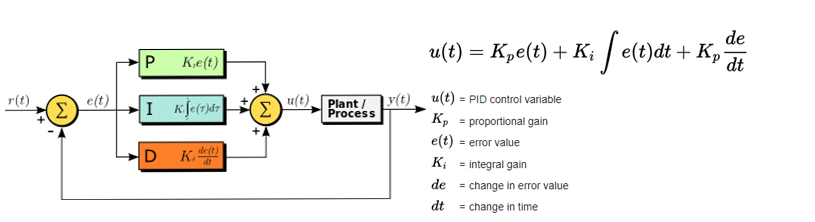
作為任何 PID 控制應用基礎的通用數學函數可以表述如下:
其中e(t)是偏差值:
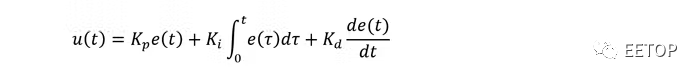
對于位置控制,r(t)為設定位置,y(t)為當前位置。

一張圖可以讓我們更直觀地理解這個數學在應用于伺服電機時是如何工作的。圖 1說明了線性伺服 PID 控制系統的框圖。
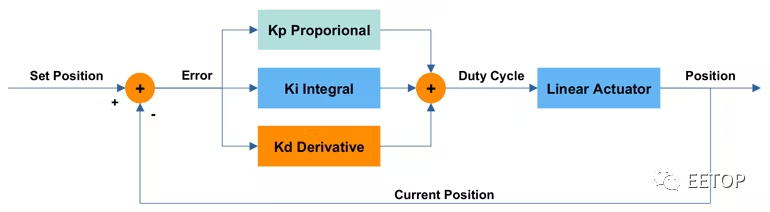
圖1、線性伺服PID控制系統。
圖 1中描繪的系統的一些關鍵元素是設置位置輸入(設定點,或我們的線性執行器的目標位置)、驅動執行器的某些占空比的脈沖寬度調制 (PWM) 信號,以及執行器的當前位置。它們分別對應于數學方程式中的量r(t)、 u(t)和y(t) 。
之所以稱為閉環控制,是因為反饋回路將有關當前狀態的信息傳遞回系統,使其能夠獲得當前狀態與所需設定點之間的差異,必須對其進行校正。具體到我們的案例,從設置位置中減去當前位置以獲得誤差(或偏差)信號,如上所示。此誤差對應于數量e(t)。
正如文章開頭提到的,PID 代表比例、積分和微分。這些是指為調節 PID 控制系統的運行而生成的三個控制信號。
如數學和圖表所示,三個控制信號由誤差信號產生,從Proportional、Integral和Derivative模塊輸出——也標有它們各自的增益K p、K i和K d ——并且是結合起來產生驅動執行器的 PWM 信號的占空比。
現在我們已經描述了系統的結構,我們想在固件中實現它。但要做到這一點,我們需要了解如何將線性致動器與微控制器連接起來。具體來說,我們如何從PID函數中獲取Duty Cycle信號來驅動執行器,以及執行器如何產生Current Position信號反饋給PID函數?
隨后,我們可以解釋如何將PID函數翻譯成用C語言編寫的固件源代碼。然后將提供一些演示工作實施的示例數據,作為理解三個 PID 控制信號的作用以及如何調整其性能的基礎。
電氣連接線性致動器
線性致動器用于提升、傾斜、拉動或推動物體(圖 2)。我們這里使用的微型線性執行器由驅動部分的直流伺服電機和位置傳感部分的電位器組成。

圖2. 線性致動器的示例。
對于該裝置,PID 控制器板需要輸出 12V PWM 信號來控制電機速度,并使用模數轉換器 (ADC) 通道來感測執行器的位置。因此,我們應該在微控制器上配置兩個 GPIO 引腳,一個用于 PWM,另一個用于 ADC。
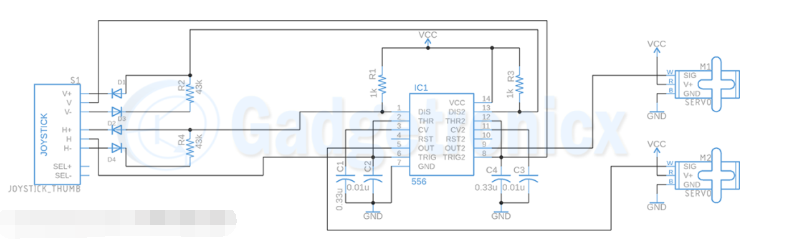
線性執行器的位置輸出是一個電阻值。如果電位器連接在電源V dd和地GND之間(圖 3),則可以將抽頭處的電阻作為簡單分壓器的輸出進行測量。位置的范圍和單位從 0 ~ 10,000 Ω 對應為 0 ~ V dd V,ADC 將電壓轉換為數字值,即我們實現的當前位置y(t)。如果 ADC 的分辨率為 10 位,則此數字值介于 0 和 1023 之間。
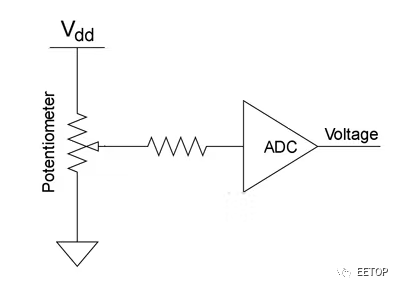
圖3、電位器ADC電路。
我們的控制器輸出u(t)也可以是表示電壓的數字值,這很方便。然而,該控制器輸出驅動線性致動器,線性致動器不期望變化的電壓作為輸入來控制其速度,而是期望具有變化占空比的固定電壓 PWM 信號。因此,需要進行轉換。
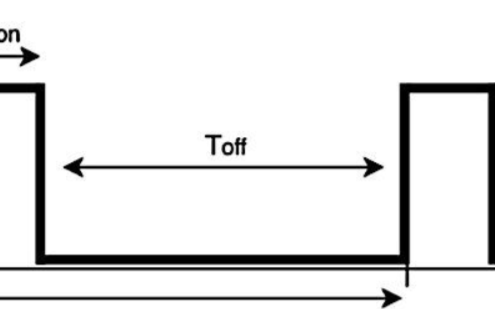
圖 4中的圖表顯示了 0 V 至 12 V 的電壓如何轉換為具有 0% 至 100% 占空比的可變寬度脈沖的 12 V PWM 信號。嚴格來說,高于 12 V 的電壓也必須考慮在內,并且必須轉換為 100% 的占空比,因為數學決不會將控制器輸出限制在 12 V 以下。
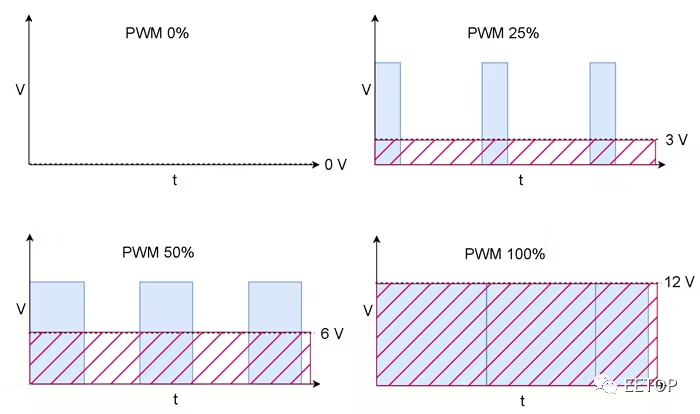
圖4. PWM 信號圖。
作為關于執行器接口的最后評論,我們應該強調,只有我們選擇的設備的速度控制和位置傳感特性的性質引導我們將 u(t) 和 y(t) 都指定為我們實施中的電壓值。這些數值沒有其他關系,如果受控設備接口的性質另有規定,在另一個應用程序中甚至可能不在同一測量單位中。
編寫固件
對于用作 PID 控制器的固件,它必須確定誤差值e(t),評估 PID 函數以調整驅動設備的信號u(t) ,并隨著時間的推移連續執行此操作。然而,對于固件執行而言,以真正連續的方式執行任務并不是一個可行的概念。最接近的是在很短的時間間隔內快速重復或迭代任務。?
如果該任務是 PID 算法,則其連續時間數學需要用離散時間版本替換,具有以下含義:
1. 固定間隔T被指定為迭代之間的時間,即它們的周期。
2. 將連續時間t時刻的誤差值e(t)的評估替換為離散時間迭代n時的評估,即e(n)?=?r(n)?–?y(n),其中n?= 0 , 1, 2, …
3. e(t)的連續時間積分由e(n)T的離散時間求和代替。
4. e(t)的連續時間導數替換為e(n)在前一次迭代和當前迭代之間的線性斜率——即:

因此,在第n次迭代中評估的離散時間輸出信號u(n)可以表示如下:
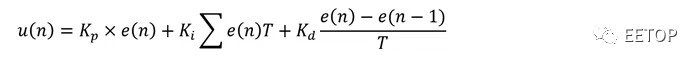
現在我們可以實現離散時間PID控制功能了。在示例 C 代碼(參見下面的代碼列表)中,變量和常量的名稱與數學方程式中的相應元素非常匹配。此代碼可以在 PID 固件的每次迭代中執行,通常在配置為每T毫秒觸發一次的定時器中斷內執行。
/* 當前誤差- 比例項 */
e = r - y;
/* 累積誤差- 積分項 */
總誤差 += e;
/* 差分誤差- 導數項 */
deltaError = e - 先前的錯誤;
/* PID控制*/
u = Kp * e + Ki * (totalError * T) + Kd * (deltaError /T);
/* 同時為下一次迭代做準備——將之前的設置為當前錯誤 */
以前的錯誤= e;
剩下要做的是為 PID 增益K p、K i、和K d以便系統在被要求移動到選定的設定點時正確執行。我們將為這些增益手動選擇不同的值,以研究它們對位置控制的影響,并在此過程中演示調整它們的通用方法。我們還將深入了解控制功能中每個術語的用途。
PID 增益調整
有幾個評估系統性能的標準,包括死區時間、上升時間、過沖、穩定時間和穩態誤差。雖然在調整 PID 增益之前應根據這些標準定義性能預期,但此類預期取決于應用程序的要求。因此,就本文而言,足以說明各種標準何時受到不同增益調整的影響。
Kp , K i , _和Kd增益將單獨調整,并按此順序,給定一個選定的設置點。更具體地說,代碼將在每次執行時將其中一個增益設置為不同的值,并將 r 的值設置為 700。
至于這個 700 值的相關性,讀者應該記得Current Position是一個數字值,表示從執行器的電位器獲得的電壓,而Current Position現在在我們的代碼中由變量 y 表示。設置位置-表示我們代碼中的變量 r - 是相同范圍內的數字值,如前所述,如果 ADC 具有 10 位分辨率,則該值介于 0 和 1023 之間。因此,700 的設定點值是合理的,盡管是任意的。
調整 K?p以接近目標位置
Kp是比例增益。控制函數的比例項通過使用與該電流誤差成比例的信號移動線性致動器來補償電流誤差。比例項用于使當前位置接近目標是有意義的,因為該誤差是執行器的設定位置與其當前位置之間的差異。比例項使控制函數尋求將其減少到零。
在調整的第一步中,我們將積分和微分增益K i和K d設置為零,并增加比例增益K p直到致動器穩定在目標位置附近 (700)。比例增益太高會引起振蕩。
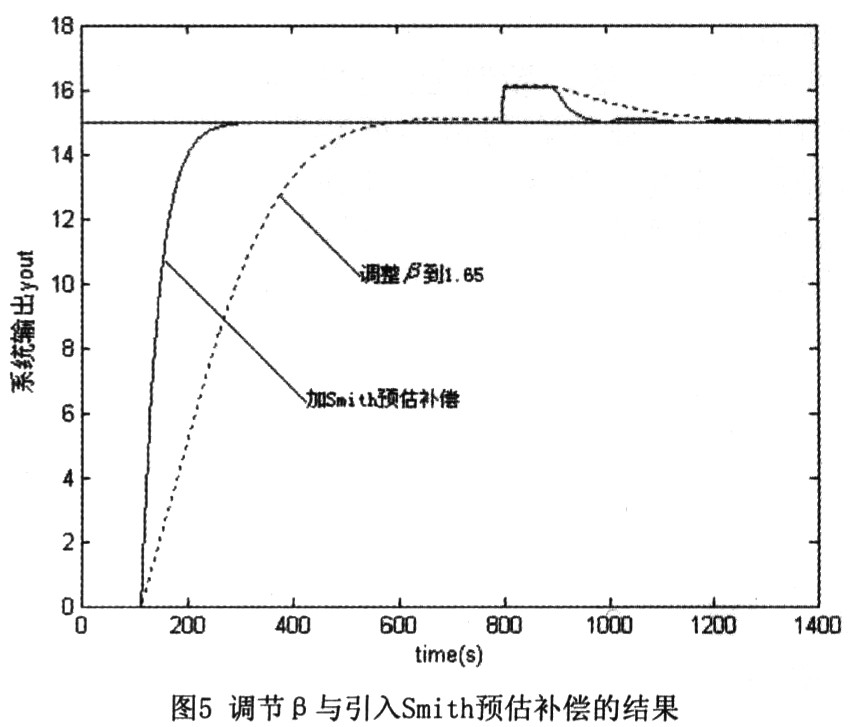
圖 5中的圖表顯示了對于不同的K p值,執行器的當前位置如何隨時間變化。我們將選擇K p = 1,觀察它會導致當前位置穩定在目標附近并且穩定時間最快。
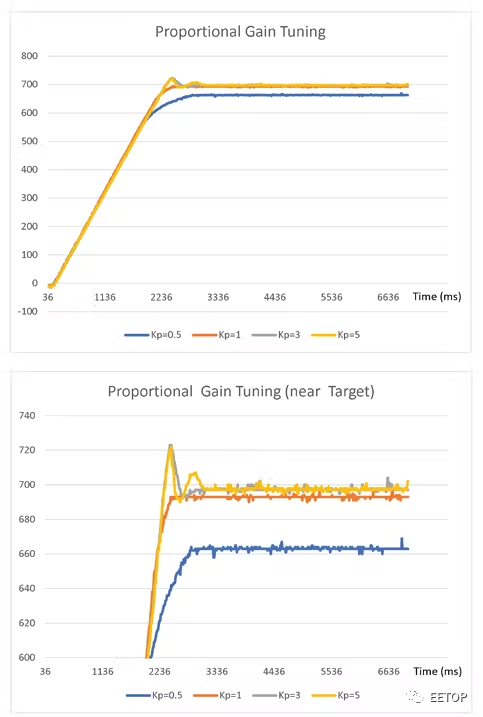
圖5.比例增益調整。
讀者會注意到有一個殘余的穩態誤差,即最終的當前位置與目標設定點位置有偏差。這種偏移在純比例控制器的情況下很常見,并且會在下一步調整積分增益時消除。
調整 K?i以消除穩態誤差
Ki是積分增益。控制函數的積分項通過使用與隨時間累積的過去誤差量成比例的信號移動線性致動器來補償過去誤差。積分項用于消除穩態誤差是有意義的,因為該誤差是一個常數偏移量,它會隨著時間的推移增加積分,從而使控制函數試圖將其減小到零。
在調整的第二步中,我們保持在第一步中選擇的比例增益K p = 1,將微分增益K d設置為零,并增加積分增益K i直到執行器穩定得更接近目標位置 (700) ——即,直到穩態誤差接近于零。
圖 6中的圖表顯示了對于K p = 1 的不同K i值,執行器的當前位置如何隨時間變化。對于一組給定的要求, Ki =?0.5的結果可能非常令人滿意,我們可能會選擇不涉及微分項,在這種情況下,解決方案將是比例積分 (PI) 控制器。
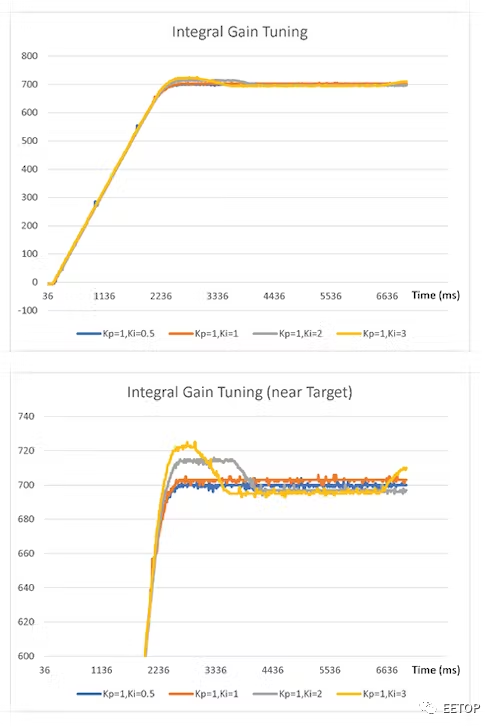
圖6.積分增益調整。
但是,或者,我們可能更愿意選擇K i = 2,這可能是由于其結果中顯示的上升時間有所改善。讀者會注意到,在這種情況下,更好的上升時間是以過沖為代價的。當在下一步中調整微分增益時,將消除這種過沖。
調整 K?d以消除過沖
Kd是微分增益。控制函數的導數項通過使用與根據誤差的時間導數(即其變化率)估計的未來誤差量成比例的信號移動線性致動器來補償未來(估計的)誤差。
微分項用于消除瞬態效應(如超調)是有道理的,它們自然反映在時間導數中,從而使控制函數尋求將它們減少到零。在存在干擾的情況下提高穩定性和縮短建立時間是額外的相關優勢。但是請注意,如果誤差信號非常嘈雜,微分項會使控制系統不穩定。
在這第三步調整中,我們保持在前兩步中選擇的比例和積分增益K p = 1 和K i = 2,并增加微分增益K d直到消除超調。微分增益太高會引起振蕩。
圖 7中的圖表顯示了對于不同的K d值,K p = 1 和K i = 2 ,執行器的當前位置如何隨時間變化。我們將選擇K d = 0.05,觀察到它有效地減少了過沖,同時保持了改進的上升時間。
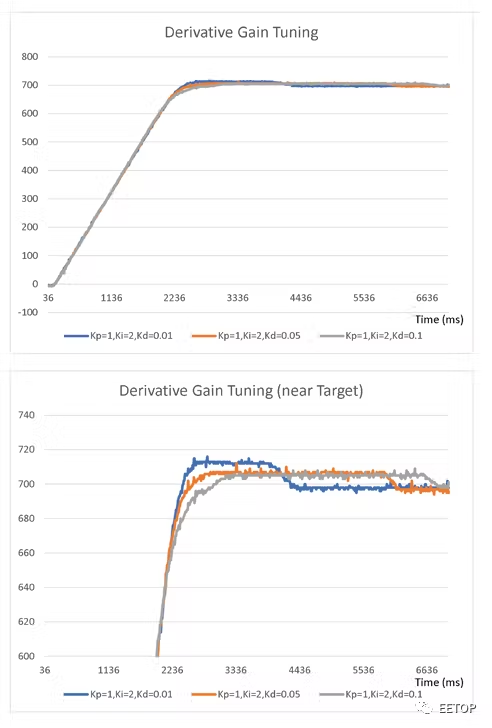
圖7. 微分增益調整。
然后,在我們的控制器版本中,啟用了所有三個信號比例、積分和微分,我們已經成功地調整了它們的增益以實現適當的控制器行為。我們還確定增益值應為K?p?= 1、K?i?= 2 和K?d?= 0.05。
結論
這篇關于 PID 控制的文章解釋了 PID 控制器核心的數學原理,并提供了一個實際示例,說明如何實現該數學原理以在微控制器上運行。討論了用于位置控制的微控制器和直流伺服電機之間的信號性質的實際考慮因素。
最后,提供了一些數據來演示如何手動調整控制函數的比例、積分和微分項以獲得適當的性能。它還讓讀者了解 PID 算法中每個函數的用途。
通用現成的 PID 控制器不是將 PID 控制設計到定制的嵌入式設備中,而是工業市場上可用的替代品,例如,其中一些基于可編程邏輯控制器 (PLC)。這些可能會滿足許多用戶的需求。
但是,如果它需要與您的工廠流程相關的非標準功能,它可能無法滿足您的應用需求。或者,如果它有特殊的數據通信需求,或者如果通用控制器具有您希望避免用于成本敏感型應用的不需要的功能。在這種情況下,定制 PID 控制器設計是一種選擇。(EETOP編譯自electronicdesign)
編輯:黃飛
?
 電子發燒友App
電子發燒友App






















評論