6.1.幾個基本定律
6.1.1畢奧-薩伐爾定律

圖6.1 畢奧薩伐爾定律
電流元Idl在空間某點P處產(chǎn)生的磁感應強度dB的大小與電流元Idl的大小成正比,與電流元Idl所在處到P點的位置矢量和電流元Idl之間的夾角的正弦成正比,而與電流元Idl到P點的距離的平方成反比。

描述的是電流元在真空任意點P處所激發(fā)的磁場的定量計算,當然P點的總磁場應為所有電流元在P點處磁感應強度dB的矢量疊加。
6.1.2.安培環(huán)路定理
畢奧-薩伐爾定律給出了由電流計算磁感應強度B的方法,由此定律可以推出:


圖6.2 安培環(huán)路定理
即安培環(huán)路定理:在真空穩(wěn)恒磁場中,磁場強度矢量H沿任何閉合路徑的線積分,等于這閉合路徑所包圍的各個電流的代數(shù)和。
在有磁介質(zhì)時,安培環(huán)路定理仍然適用,但磁場強度H取值應為:H=B/μ0-M。
6.1.3.全電流定律
全電流定律是由麥克斯韋將安培環(huán)路定理進行推廣,任意一個閉合回線上的總磁壓等于被這個閉合回路所包圍的面內(nèi)穿過的全部類型電流的代數(shù)和。

安培環(huán)路定理不適用于非恒定電流,比如在電容器兩極板間取一閉合曲面,由于曲面沒有包圍傳導電流(媒介中由電荷的運動產(chǎn)生的電流),所以安培環(huán)路定理右邊為零;若在有傳導電流處取回路,電流和是不為零的,導致運用安培環(huán)路定理的時候出現(xiàn)了矛盾;
麥克斯韋提出假設:變化的電場能在其周圍激發(fā)磁場,定義電場的變化率為位移電流,位移電流不是電荷作定向運動的電流,但它能引起的變化磁場,與傳導電流引起的變化磁場等效。
全電流是指通過空間某截面的電流應包括傳導電流與位移電流之和;全電流是連續(xù)的,在空間構成閉合回路。導線中有傳導電流,而電容器中有位移電流,即傳導電流中斷處,有位移電流接續(xù),此時安培環(huán)路定理就成立了,因此全電流定律是安培環(huán)路定理的補充,同時也是麥克斯韋預言電磁波存在的理論基礎之一。
6.2磁路
6.2.1 磁路的定義及構成
磁通量所通過的磁介質(zhì)的路徑稱為磁路;
與電路電流優(yōu)先從電導率高的路徑通過類似,磁通優(yōu)先從磁導率高的介質(zhì)中通過,但導磁材料磁導率一般是非導磁材料的幾千倍,與電路中導電材料是非導電材料的幾千億倍相差較大,因此磁路設計中有時需要考慮漏磁的因素。

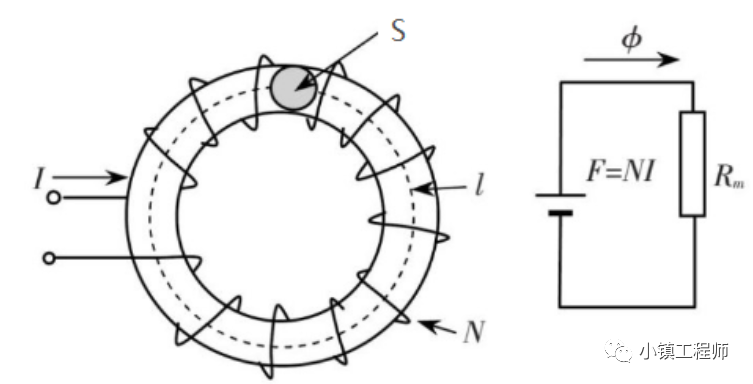
圖6.3 磁路示意圖
典型磁路構成:
1.磁源:通電線圈或永磁體,產(chǎn)生磁勢;磁勢也稱磁動勢,用F表示,為磁路磁場應力,類似于電學中的電動勢或電壓,單位為A*匝 (安培匝)。
2.高磁導鐵芯:目的是使磁通集中在指定的路徑上并獲取較強的磁感應強度,用軟磁材料制成指定形狀的鐵心來實現(xiàn)。
3.空氣隙:在電機的定轉(zhuǎn)子之間存在空氣隙,也是磁路的組成部分;一些特殊磁路中如變壓器是可以不存在氣隙的。

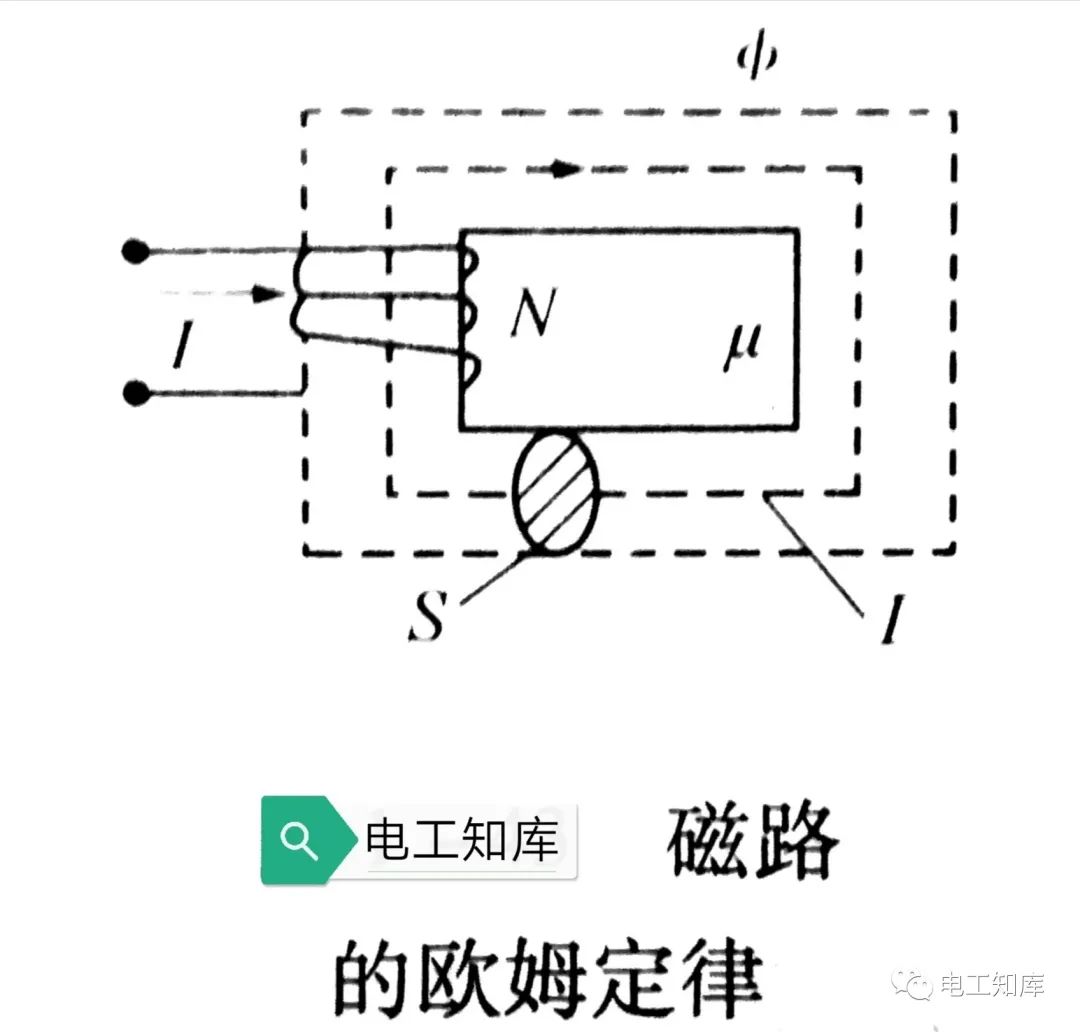
圖6.4 電機磁路示意圖
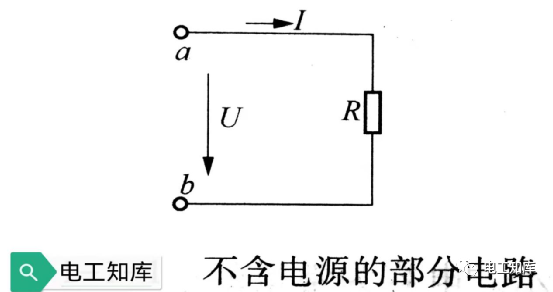
6.2.2磁路的歐姆定律
假設均勻磁路:鐵芯截面積為S,周長為l,磁導率為μ,鐵芯上繞以匝數(shù)為N、電流為i的通電線圈,計算其磁路特征量:

圖6.5 均勻磁路
根據(jù)安培環(huán)路定理可知:

假設磁路無漏磁,磁場全部從鐵芯中經(jīng)過,且鐵芯截面各處磁感應強度B均相等且與截面S垂直,定義磁通量為磁感應強度B與面積S的乘積,簡稱磁通(Magnetic Flux),磁通為標量,用“Φ”表示。
磁通Φ:


由上面的磁路,可參照電路圖的方式畫出其磁路圖:

圖6.6 磁路圖
6.2.3磁路的基爾霍夫定律
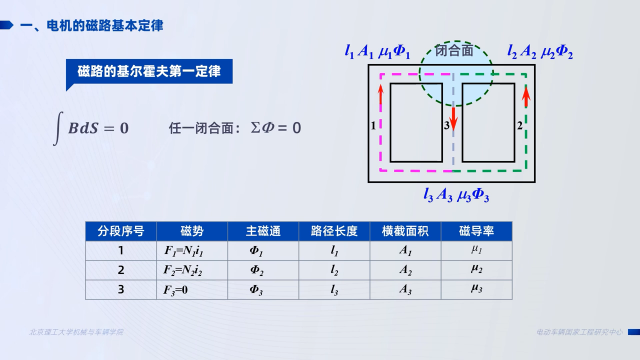
磁路的基爾霍夫第一定律:由于磁感線是封閉曲線,無頭無尾,因此磁路中任一節(jié)點處,進入該處的磁通與離開該處的磁通代數(shù)和應為零,表達式為:

磁路的基爾霍夫第二定律:由全電流定律可以推出,任一閉合磁路中各段磁壓的代數(shù)和等于環(huán)繞這個回路所有磁動勢的代數(shù)和,表達式為:

由于磁路與電路的相似性,二者各基本參數(shù)及定律的類比關系見下表:
表6.1 磁路與電路類比

6.2.4磁路的串聯(lián)、并聯(lián)

有如下圖磁路

圖6.7 磁路的串并聯(lián)
各變量間關系如下:

6.3氣隙
6.3.1氣隙定義及特征
在電磁鐵及電機的磁路結構中都包含氣隙,電機中氣隙指的是電機定子和電機轉(zhuǎn)子之間的間隙。
氣隙的邊緣效應和漏磁效應:
由于氣隙的磁阻為鐵芯磁阻的幾千倍,因此a與b之間的磁位差足以引起氣隙間磁力線向外擴散,導致磁力線經(jīng)過的面積變大,即氣隙的邊緣效應,甚至有少量磁力線不通過氣隙,直接從c到d,即漏磁。

圖6.8 氣隙的邊緣效應及漏磁
由于氣隙的漏磁效應,氣隙的有效截面積并不等于鐵芯的截面積,現(xiàn)實中若氣隙長度不超過氣隙處鐵芯截面尺寸的15%-20%且氣隙兩邊的鐵芯端面平行稱為短氣隙,其有效截面積可根據(jù)經(jīng)驗公式計算:
(1)氣隙兩邊端面同軸、平行、截面尺寸相同,則氣隙的有效截面為尺寸可將截面的長/寬各增加一個氣隙長度,若是圓形則將直徑增加一個氣隙長度。


圖6.9 鐵心兩端等面積氣隙
(2)若兩端面同軸、平行、截面尺寸差異較大,則氣隙的有效截面尺寸為將小截面邊長均增加兩個氣隙長度,若是圓形則將小截面的直徑增加兩個氣隙長度;即:


圖6.10 鐵心兩端不等面積氣隙
6.3.2存在氣隙的磁路的計算

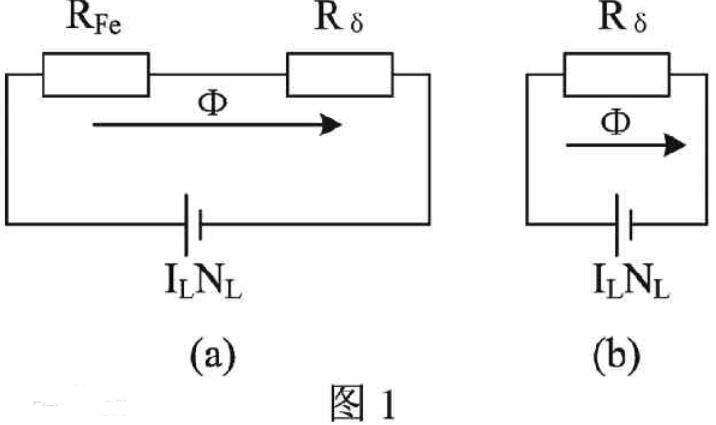
圖6.11 存在氣隙的磁路
假設氣隙δ足夠小,磁路無漏磁,計算鐵心及氣隙處的磁勢、磁阻、磁通、磁感應強度等量:
(1)磁動勢:整個系統(tǒng)的磁動勢為通以電流i的N匝繞組,系統(tǒng)的總磁勢為

(2)磁阻及磁導:由于系統(tǒng)假設為無漏磁,因此磁力線只從鐵心及氣隙中通過,因此磁路可以簡化為鐵心與氣隙串連起來的磁路,磁路的磁阻為鐵心磁阻與氣隙磁阻之和;

(3)磁通
磁路的磁通為:

磁通為連續(xù)量,不管在氣隙或鐵心,其磁通是相等的。
(4)磁位降及磁場強度
磁路某段的磁場強度與其路徑長度的乘積為此段磁路的磁位降,數(shù)值上等于磁通與磁阻之積,磁路上串連的總磁位降之和為磁動勢。

由于鐵心磁導率為空氣磁導率的幾千倍(如硅鋼大約為空氣的8000倍左右),由式6.26可知,雖然氣隙較短,但一般氣隙的磁壓降較鐵心大的多。

(5)磁通密度:
假設鐵心及氣隙的橫截面中,磁力線分布均勻,定義磁通密度為磁通除以磁路的面積,使用B表示:

結合前文磁感應強度的介紹,磁通密度與磁感應強度可以認為是同一個值,這也是為什么磁通密度與磁感應強度都使用B來表示。
根據(jù)式6.33及6.34可知,鐵心和氣隙處的磁通密度是不相等的。
根據(jù)上面的計算,以上磁路中重要的幾個量均可以使用已知量計算得出,這些已知量包括:電流i、匝數(shù)N、鐵心平均長度lFe、鐵心橫截面積SFe、鐵心磁導率μ、氣隙長度δ、氣隙面積Sg、真空磁導率μ0(這里空氣隙的磁導率使用真空磁導率表示),如圖6.11所示。
6.4 永磁體的等效
6.4.1 磁路中的永磁體等效原理
永磁體作為磁源與電流類似,會產(chǎn)生相應的磁動勢,但同時又是磁路的一部分,并且由于永磁體存在退磁曲線及回復曲線,且有些永磁材料兩個曲線并不重合,因此永磁體的工作狀態(tài)很復雜,這里假設永磁體為稀土永磁體,其退磁曲線接近直線,且回復線與退磁曲線相重合。
假設永磁體工作在恒定的磁場中,只需要將永磁體作為恒定的磁源串連或并聯(lián)到磁路中即可,但當其工作在交變的磁場中,比如永磁同步電機,可以按照等效磁通或等效磁勢的方法進行等效。
6.4.2等效磁通
永磁電機在運行時,將永磁體等效為一個恒磁通源Φr與一個恒定磁導Λr相并聯(lián)的磁通源:其中為Φr永磁體虛擬內(nèi)稟磁通,對于給定性能和尺寸的永磁體,它是一個常數(shù):

其中Sm為永磁體提供每極磁通的截面積;Br為剩余磁感應強度。
Λr為永磁體的內(nèi)磁導,對于給定性能和尺寸的永磁體,它也是一個常數(shù):

hMp為每對極磁路中永磁體磁化方向的長度(m),μr為相對回復磁導率,是永磁體固有參數(shù),μ0為真空磁導率。

圖6.12 永磁體等效為恒定磁通并聯(lián)磁導(磁阻)
6.4.3等效磁勢
上述磁通源也可等效變換為磁動勢源Fr與一個恒定內(nèi)磁導Λr相串聯(lián)的磁動勢源:
對于給定性能和尺寸的永磁體,F(xiàn)r為常數(shù):

Hc為永磁體矯頑力,hMp為每對極磁路中永磁體磁化方向的長度,Λr數(shù)值見上。

圖6.13 永磁體等效為恒定磁勢串連磁導(磁阻)
 電子發(fā)燒友App
電子發(fā)燒友App



























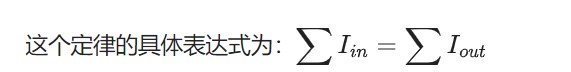










評論