前言

SVPWM調制直接著眼于如何使負載電機獲得圓形旋轉磁場，這與現代電機控制常用的磁場定向控制的思路高度吻合，因此在電機控制領域獲得了廣泛的應用，那么電控小白今天就來和大家說一說SVPWM到底是怎么回事。

SVPWM調制全稱為空間電壓矢量PWM調制，它可以使逆變器輸出線電壓最大幅值達到母線電壓Udc。

PWM發波的基礎-面積等效

我們以一個簡單的拓撲來說明PWM調制的基本原理。

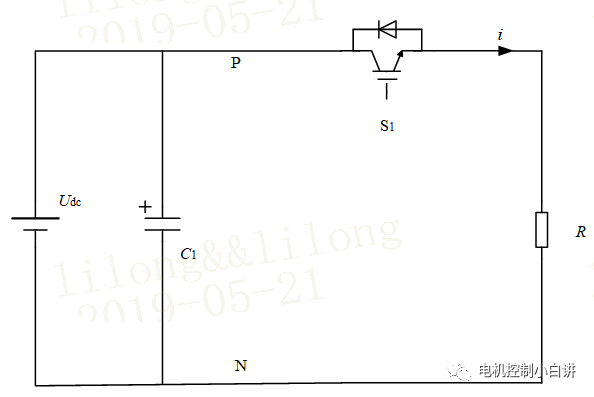
工況1：S1導通，此時負載R上的電壓Udc；

工況2：S1關斷，此時負載R上的電壓0；

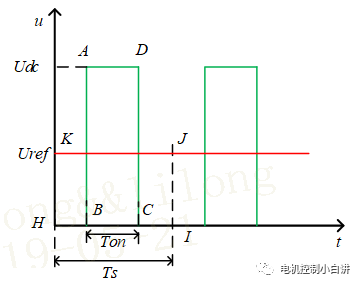
如果我們想給負載R施加一個電壓Uref，且滿足0≤Uref≤Udc，那我們怎么實現呢？

假定控制S1以Ts為周期進行開通關斷切換，同時導通時間為Ton，那么在負載R上就可以獲得如圖中綠色曲線所示的電壓波形。

如果我們保證Ton滿足以下約束條件：

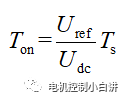
那么綠色曲線形成的電壓脈沖在Ts內的平均值就等于Uref。同時對于矩形ABCD和HIJK的面積相等：

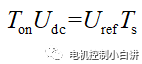
利用面積相等的周期性脈沖電壓來等效穩定直流電壓的方法即面積等效原理。

基于面積等效原理，我們就能利用脈沖電壓等效我們期望的其他直流輸出電壓。

如果我們輸出的脈沖電壓的脈沖寬度按正弦規律變化，那么我們就能得到等效電壓按正弦規律變化的一系列脈沖電壓，而這一系列脈沖電壓組合在一起就構成了完整的正弦電壓。

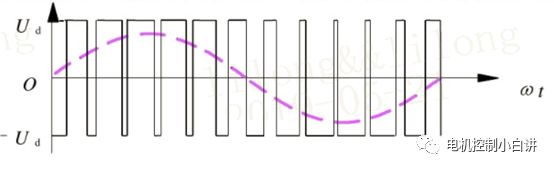
三相逆變器如何驅動？

三相逆變器由三個橋臂6個開關器件構成，忽略死區時間，同一橋臂上下兩個開關器件互補導通。對于每一個橋臂，上管導通，輸出電壓為Udc，下管導通，輸出電壓為0。

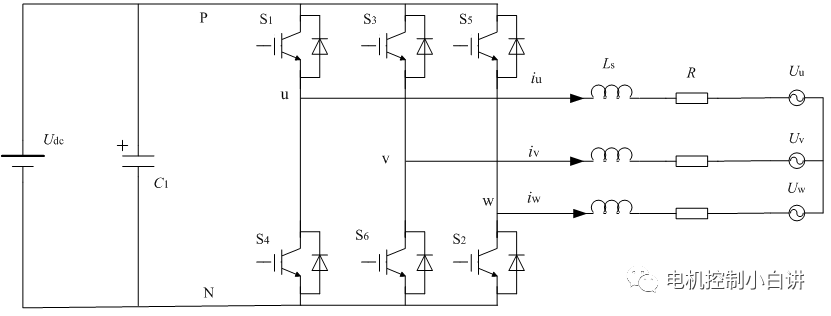
為了方便分析，我們假設上橋臂開關器件導通、下橋臂關斷狀態為1，上橋臂器件關斷、下橋臂導通狀態為0。

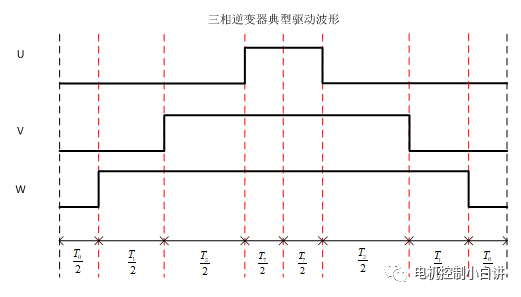
基于以上假設，三相逆變器的橋臂器件不同的開關狀態組合一共有8個，分別為（000）、（100）、（010）、（001）、（110）、（101）、（011）和（111），這八種不同的開關狀態組合就構成了SVPWM調制的8個基本電壓矢量。在這8個矢量中，（000）和（111）分別對應上管全開（下管全關）和下管全開（上管全關）狀態；在這兩種狀態下，等效將輸出的三相短路，這時候作用到負載上的線電壓為0，所以這兩個狀態被稱為零矢量，而其余6個為有效矢量。

如何理解8個基本電壓矢量？

前面說到了SVPWM調制的基礎是8個基本電壓矢量，那么這8個基本電壓矢量怎么理解呢？

我們以矢量（100）來說明這個問題，（100）表示U相上橋導通，V和W相下橋導通，這時候負載的等效電路如下圖所示。

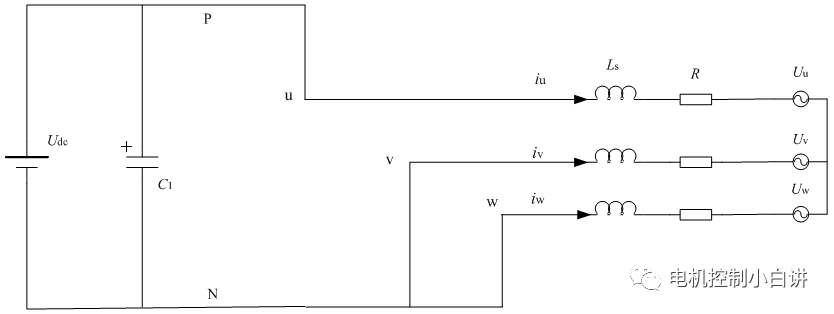
從圖中可以看出，負載側為V和W并聯，然后和U相串聯；電機三相的阻抗相等， V和W并聯阻抗為U相的一半，所以這時候作用到U、V、W三相的電壓為：

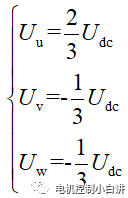
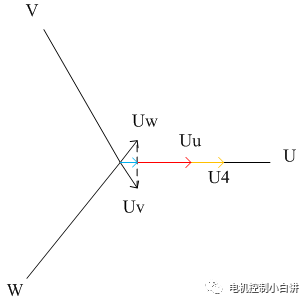
UVW在空間上構成三相靜止坐標系，可以畫出三相電壓在靜止坐標系的分布如下圖：Uu在U軸正方向，Uv在V軸負方向，Uw在W軸負方向 。Uv和Uw兩個矢量在U軸的投影為正方向，幅值均為（1/6）Udc，所以合成矢量U4（100）在U軸正方向，幅值為Udc。

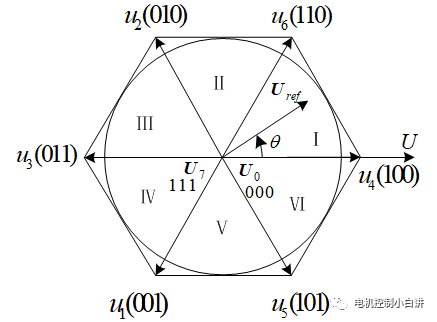
利用同樣的方法，可以分析出另外五個有效矢量在三相坐標的分布情況，這六個基本電壓矢量就夠成了我們常說的SVPWM電壓六邊形，SVPWM調制輸出的所有電壓都無法超出這個六邊形的范圍；6個有效電壓矢量將整個六邊形等分為6個扇區。

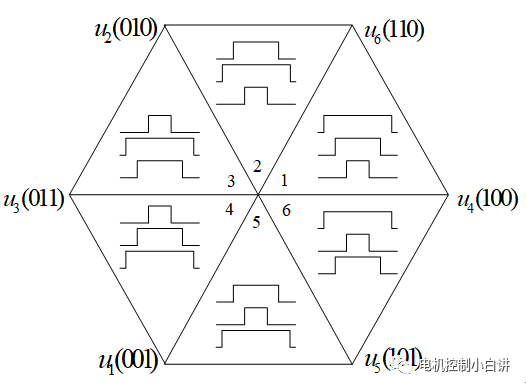
可能大家會記不清這6個基本電壓矢量的位置分布，在這里，電控小白提供一個簡單的方法：

1、這6個基本電壓矢量其實都是分布在UVW三相坐標系的坐標軸正負方向上。

2、對于上橋只有一個開關器件導通的矢量（u4(100)、u2(010)和u1(001)），我們可以發現：u4(100)是u相上橋導通，而它在U軸正方向上；u2(010)是v相上橋導通，而它在V軸正方向上；u1(001)是w相上橋導通，而它在w軸正方向上；因此對于上橋只有一個器件導通的矢量，哪一相導通，它就分布在對應的坐標軸正方向上。利用這個方法我們就能很簡單畫出三相坐標軸正方向上的矢量分布。

3、對于上橋兩個開關器件導通的矢量（u6(110)、u3(011)和u5(101)），我們可以發現：同一個坐標軸上的兩個矢量，它們的對應關系是開關狀態按位取反，比如坐標軸V上的矢量，正方向是u2(010)，那么將（010）按位取反得到（101），則V軸負方向上的矢量為u5(101)。

如何理解有效電壓矢量幅值為（2/3）Udc？

也許很多人會奇怪：其他文獻都是說SVPWM的基本電壓矢量幅值是（2/3）Udc，但我們前面分析的矢量幅值是Udc呢？

其實這個問題不難理解，對于三相對稱的正弦電壓

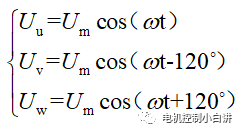
我們知道在三相靜止坐標系下，其合成矢量為逆時針方向旋轉的電壓矢量，旋轉角速度為w，矢量幅值為（3/2）Um。

這時候為了方便分析，我們可以將其乘以一個系數（2/3）作為合成矢量的幅值，這樣得到的合成矢量幅值就與相電壓的幅值相等，這種坐標變換的方法就是我們常說的等幅值變換。

所以我們常說的基本電壓矢量幅值為（2/3）Udc都是基于等幅值變換而言的，如果采用非等幅值變換，SVPWM的基本電壓矢量幅值就不在是（2/3）Udc，這個問題電控小白將在后續的文章為大家說明。

為了方便大家理解，后文的分析均針對等幅值變換。

如何利用基本電壓矢量輸出任意電壓呢？

有了8個基本電壓矢量，我們就可以利用矢量分解與合成的方法去構建電壓六邊形內的任意電壓矢量，這就是SVPWM發波的基本思路。

假定我們想輸出一個第一扇區的矢量Uref，與在靜止坐標系下的角度（與U軸的夾角，逆時針為正）為θ，那我們如何利用8個基本電壓矢量來實現它呢？

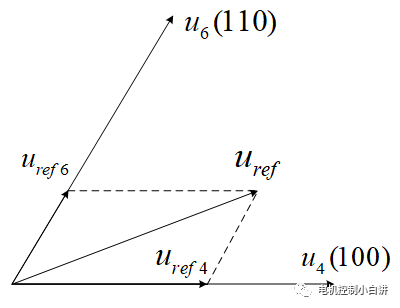
我們可以用Uref4和Uref6來合成Uref，它們的關系滿足：

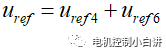
具體可以依據下面的步驟完成。

1、 根據扇區號確定用于合成的兩個基本電壓矢量：u4（100）和u6（110）。同時假定上橋臂導通一個器件的基本矢量為V1，作用時間T1；上橋臂導通兩個器件的基本矢量為V2，作用時間為T2；零矢量均用V0表示，作用時間T07。

2、 根據角度θ和扇區號，確定Uref與上橋只導通一個開關器件的基礎電壓矢量的角度θ1；舉例說明：如果Uref在第一扇區，θ1就是Uref和u4（100）之間的角度，即θ1=θ；如果Uref在第二扇區，θ1就是Uref和u2（010）之間的角度，即θ1=120°-θ。

3、 根據矢量合成的原理，需要滿足

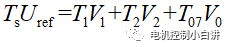
然后根據矢量關系，我們可以推到出

4、 利用計算的T1、T2和T07計算UVW三相對應的導通時間，根據前文的典型驅動波形，可以將三相驅動波形按高電平占空比時間大小區分為Tmax、Tmid和Tmin，并按下式計算

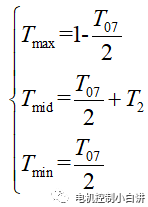
然后結合扇區號，將Tmax、Tmid和Tmin按對應關系賦值給U、V和W即可。

通過上面的方法，不論我們想輸出什么樣的三相電壓，我們都可以將它進行坐標變換，轉換為電壓矢量，然后利用SVPWM調制實現。

工程實現上的比較值如何理解

在實際的工程應用上，我們實現SVPWM都會借助微處理器（DSP、單片機）的發波模塊來實現。這里以常用的三角波模式（增減計數）來說明。

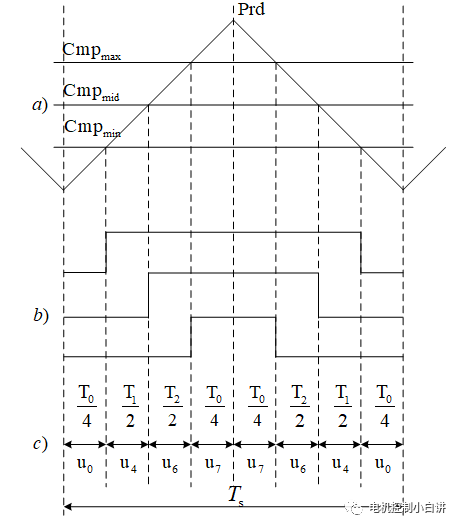
從比較值的計算和圖形，其實我們可以發現一些有趣的東西：

1、對于常規的SVPWM，CmpMax到計數器周期點的距離其實與CmpMin到0的距離相等，這里體現的正好是兩個零矢量（u0（000）和u7（111））的作用時間相等，兩者等分零矢量時間T07。

2、CmpMax和CmpMin之間的距離體現的是有效時間V1和V2的作用時間之和；

3、CmpMid的作用是使兩個有效電壓矢量進行切換，即決定兩個有效電壓矢量分別的作用時間。

非等分零矢量如何理解？

那么如果我們保持CmpMax、CmpMid和CmpMin三者的相對位置不變，同時對它們進行上下移動，這時候會怎么樣呢？

基于前面的分析，只要我們保持CmpMax、CmpMid和CmpMin三者之間的相對位置不變，有效矢量V1和V2的作用時間就不會改變，任然可以滿足

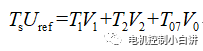
只要上式成立，那么合成電壓矢量就還是我們期望的電壓輸出；因此同時上下移動比較值，對合成電壓矢量沒有影響，那么它會對什么產生影響呢？

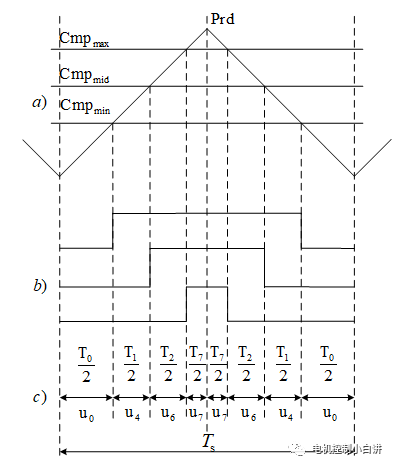
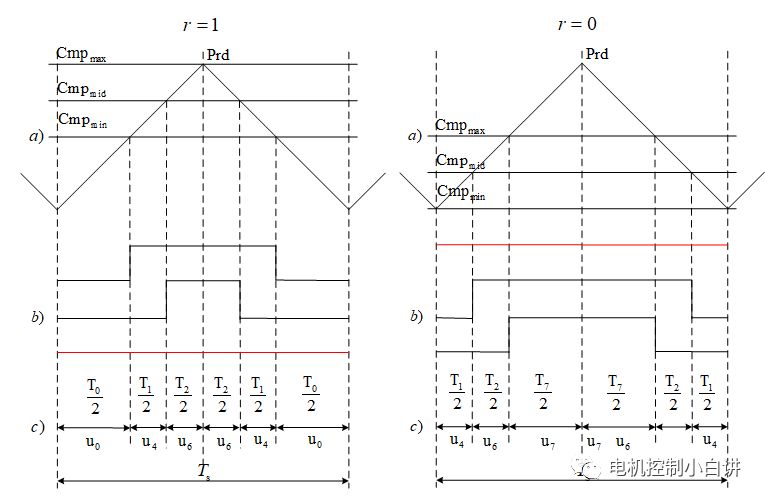
其實從調制波形不難看出，這種上下移動改變的是兩個零矢量（000）和（111）之間的時間分配，移動之后，U0和U7就不在等分零矢量時間。

為了說明這個問題，我們定義一個系數r，它滿足：

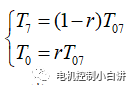
1、當r=1，CmpMax對應的橋臂一直維持0狀態，零矢量全部由U0實現；

2、當r=0，CmpMin對應的橋臂一直維持1狀態，零矢量全部由U7實現；

3、當r=0.5，與常規的CPWM模式一致，零矢量由U0和U7平分構成。

因此r=0和r=1其實是兩種不同的DPWM模式。

CPWM和DPWM模式下，輸出電流的諧波成分和THD均存在差異。我們可以通過仿真數據來具體說明一下：電流的基波頻率為20Hz，開關頻率為2kHz。

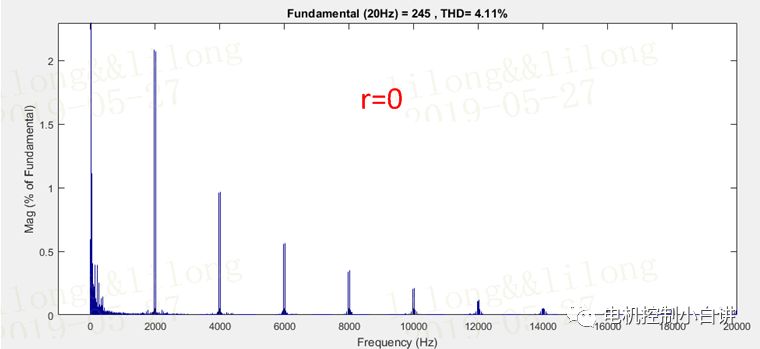
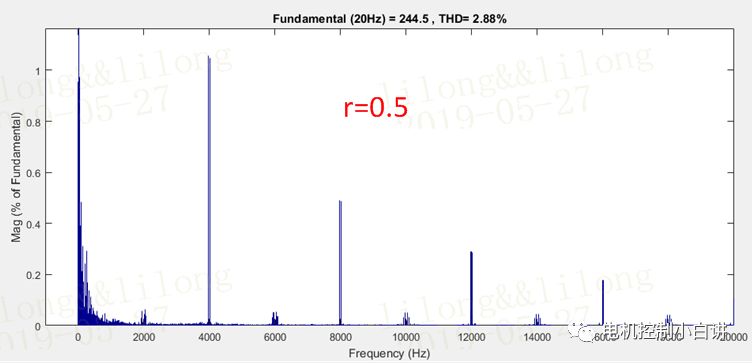
1、對于傳統CPWM發波方式，電流中的諧波成分主要分布在2倍開關頻率的倍頻次；

2、對于DPWM發波方式，電流中的諧波成分主要分布在載頻的倍頻次，而且THD大于CPWM模式。

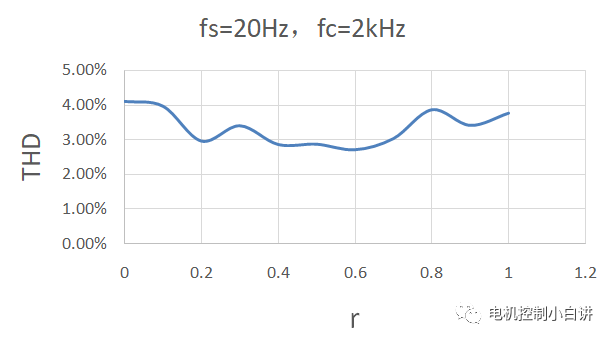
通過仿真我們可以得到不同r下的電流THD分布情況：

1、隨著r取值的變化，電流的THD會發生變化；

2、r=0.5時，電流的THD接近最小。

r對我們工程應用的價值

對于r取值會影響輸出電流諧波成分及THD這一特性對于我們實際工程應用是具有重要價值的。

對于幾百千瓦甚至上兆瓦級別的電機控制器而言，因為輸出電流極大，為了降低開關器件上的損耗，系統開關頻率一般都設置的較低（1kHz或者更低）。電機控制器在如此低的開關頻率下運行，系統的電磁噪音將會十分明顯，同時因為系統開關頻率只有1kHz，傳統的降噪方法（隨機開關頻率調制）效果將大打折扣。

這時候我們不妨讓r按一定的序列實時變化，這樣電流中的諧波成分也將實時變化，而不在是集中在某幾個頻率點附近。

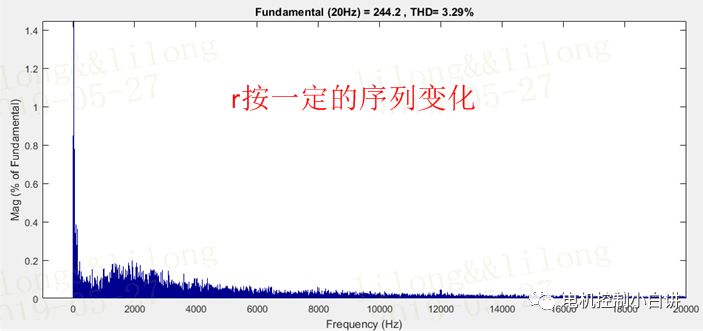
從仿真波形可看出，電流中的諧波成分主要均勻分布在低頻區域，不會出現在噪音集中的頻率點，這時候控制器的電磁噪音將從刺耳的高頻轉變為低沉的聲音。