蟻群算法是什么
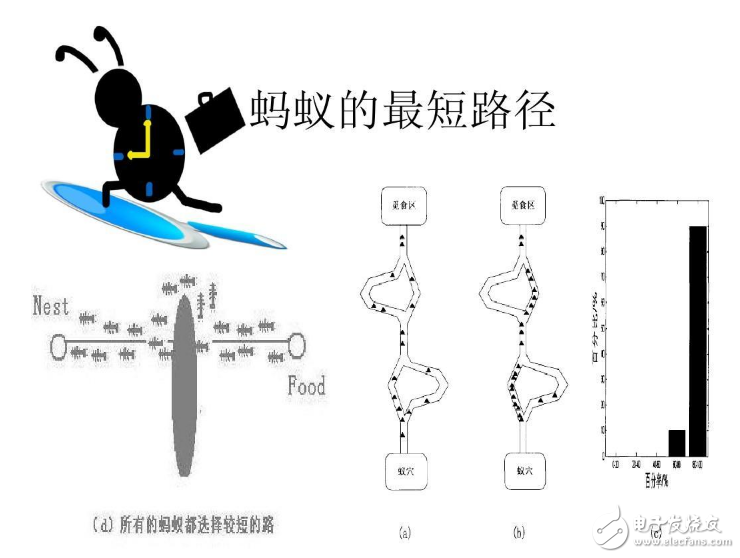
蟻群算法是一種群智能算法,也是啟發式算法。基本原理來源于自然界螞蟻覓食的最短路徑原理。
(一)蟻群算法的由來
蟻群算法最早是由Marco Dorigo等人在1991年提出,他們在研究新型算法的過程中,發現蟻群在尋找食物時,通過分泌一種稱為信息素的生物激素交流覓食信息從而能快速的找到目標,據此提出了基于信息正反饋原理的蟻群算法。
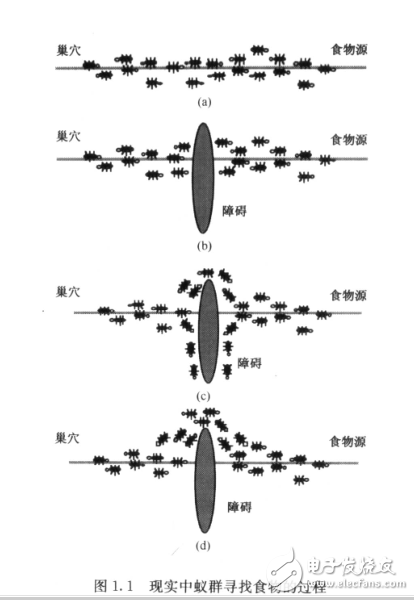
蟻群算法的基本思想來源于自然界螞蟻覓食的最短路徑原理,根據昆蟲科學家的觀察,發現自然界的螞蟻雖然視覺不發達,但它們可以在沒有任何提示的情況下找到從食物源到巢穴的最短路徑,并在周圍環境發生變化后,自適應地搜索新的最佳路徑。
螞蟻在尋找食物源的時候,能在其走過的路徑上釋放一種叫信息素的激素,使一定范圍內的其他螞蟻能夠察覺到。當一些路徑上通過的螞蟻越來越多時,信息素也就越來越多,螞蟻們選擇這條路徑的概率也就越高,結果導致這條路徑上的信息素又增多,螞蟻走這條路的概率又增加,生生不息。這種選擇過程被稱為螞蟻的自催化行為。對于單個螞蟻來說,它并沒有要尋找最短路徑,只是根據概率選擇;對于整個蟻群系統來說,它們卻達到了尋找到最優路徑的客觀上的效果。這就是群體智能。
(二)蟻群算法能做什么
蟻群算法根據模擬螞蟻尋找食物的最短路徑行為來設計的仿生算法,因此一般而言,蟻群算法用來解決最短路徑問題,并真的在旅行商問題(TSP,一個尋找最短路徑的問題)上取得了比較好的成效。目前,也已漸漸應用到其他領域中去,在圖著色問題、車輛調度問題、集成電路設計、通訊網絡、數據聚類分析等方面都有所應用。
(三)蟻群算法的流程步驟
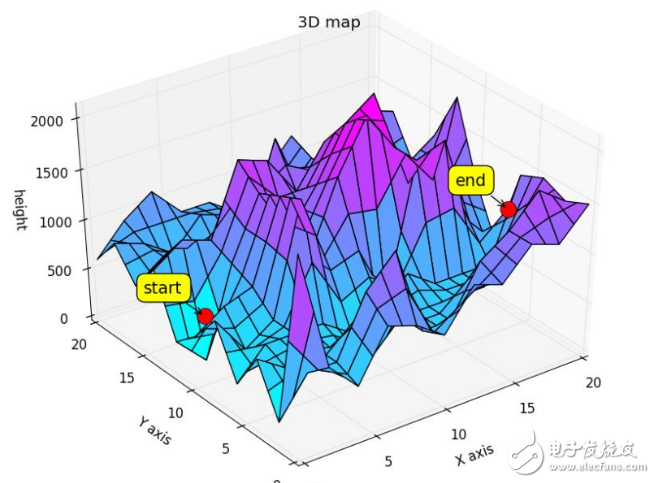
這里以TSP問題為例,算法設計的流程如下:
步驟1:對相關參數進行初始化,包括蟻群規模、信息素因子、啟發函數因子、信息素揮發因子、信息素常數、最大迭代次數等,以及將數據讀入程序,并進行預處理:比如將城市的坐標信息轉換為城市間的距離矩陣。
步驟2:隨機將螞蟻放于不同出發點,對每個螞蟻計算其下個訪問城市,直到有螞蟻訪問完所有城市。
步驟3:計算各螞蟻經過的路徑長度Lk,記錄當前迭代次數最優解,同時對路徑上的信息素濃度進行更新。
步驟4:判斷是否達到最大迭代次數,若否,返回步驟2;是,結束程序。
步驟5:輸出結果,并根據需要輸出尋優過程中的相關指標,如運行時間、收斂迭代次數等。
要用到的符號說明:
初始時刻螞蟻被放在不同的城市,且各城市路徑上的信息素濃度為0。
由于蟻群算法涉及到的參數蠻多的,且這些參數的選擇對程序又都有一定的影響,所以選擇合適的參數組合很重要。蟻群算法有個特點就是在尋優的過程中,帶有一定的隨機性,這種隨機性主要體現在出發點的選擇上。蟻群算法正是通過這個初始點的選擇將全局尋優慢慢轉化為局部尋優的。參數設定的關鍵就在于在“全局”和“局部”之間建立一個平衡點。
(四)蟻群算法的關鍵參數
在蟻群算法的發展中,關鍵參數的設定有一定的準則,一般來講遵循以下幾條:
盡可能在全局上搜索最優解,保證解的最優性;
算法盡快收斂,以節省尋優時間;
盡量反應客觀存在的規律,以保證這類仿生算法的真實性。
蟻群算法中主要有下面幾個參數需要設定:
(下面列的是一些書上的主要結論,實驗過程就不舉例了,具體參考《MATLAB在數學建模中的應用》)
螞蟻數量:
設M表示城市數量,m表示螞蟻數量。m的數量很重要,因為m過大時,會導致搜索過的路徑上信息素變化趨于平均,這樣就不好找出好的路徑了;m過小時,易使未被搜索到的路徑信息素減小到0,這樣可能會出現早熟,沒找到全局最優解。一般上,在時間等資源條件緊迫的情況下,螞蟻數設定為城市數的1.5倍較穩妥。
信息素因子:
信息素因子反映了螞蟻在移動過程中所積累的信息量在指導蟻群搜索中的相對重要程度,其值過大,螞蟻選擇以前走過的路徑概率大,搜索隨機性減弱;值過小,等同于貪婪算法,使搜索過早陷入局部最優。實驗發現,信息素因子選擇[1,4]區間,性能較好。
啟發函數因子:
啟發函數因子反映了啟發式信息在指導蟻群搜索過程中的相對重要程度,其大小反映的是蟻群尋優過程中先驗性和確定性因素的作用強度。過大時,雖然收斂速度會加快,但容易陷入局部最優;過小時,容易陷入隨機搜索,找不到最優解。實驗研究發現,當啟發函數因子為[3,4.5]時,綜合求解性能較好。
信息素揮發因子:
信息素揮發因子表示信息素的消失水平,它的大小直接關系到蟻群算法的全局搜索能力和收斂速度。實驗發現,當屬于[0.2,0.5]時,綜合性能較好。
信息素常數:
這個參數為信息素強度,表示螞蟻循環一周時釋放在路徑上的信息素總量,其作用是為了充分利用有向圖上的全局信息反饋量,使算法在正反饋機制作用下以合理的演化速度搜索到全局最優解。值越大,螞蟻在已遍歷路徑上的信息素積累越快,有助于快速收斂。實驗發現,當值屬于[10,1000]時,綜合性能較好。
最大迭代次數:
最大迭代次數值過小,可能導致算法還沒收斂就已結束;過大則會導致資源浪費。一般最大迭代次數可以取100到500次。一般來講,建議先取200,然后根據執行程序查看算法收斂的軌跡來修改取值。
蟻群算法的優勢在哪里?
圖論中很多問題都是求某個規則下的最短路徑,但因為規則不同,這些問題也有著本質上的不同,不能簡單地都歸于“最短路徑”問題,某些問題已有有效算法,有些問題至今沒有有效算法。
Prime 算法和 Kruskal 算法都是用來求加權連通簡單圖中權和最小的支撐樹(即最小樹)的,Prime算法的時間復雜度為O(n^2) (n 為頂點數),Kruskal 算法的時間復雜度為 O(eln(e)) (e為邊數),這兩種算法都是多項式時間算法,也就是說,最小樹問題已經有了有效算法去求解,屬于P問題。
Dijkstra 算法求解的是加權連通簡單圖中一個頂點到其它每個頂點的具有最小權和的有向路,最簡單版本的時間復雜度是O(n^2),也是多項式時間算法。
而蟻群算法是一種近似算法,它不是用來解決已存在精確有效算法的問題的,而是用來解決至今沒有找到精確的有效算法的問題的,比如旅行商問題(TSP)。
旅行商問題也可以說是求“最短路徑”,但它是求一個完全圖的最小哈密頓圈,這個問題至今未找到多項式時間算法,屬于NPC問題,也就是說,當問題規模稍大一點,現有的精確算法的運算量就會急劇增加。
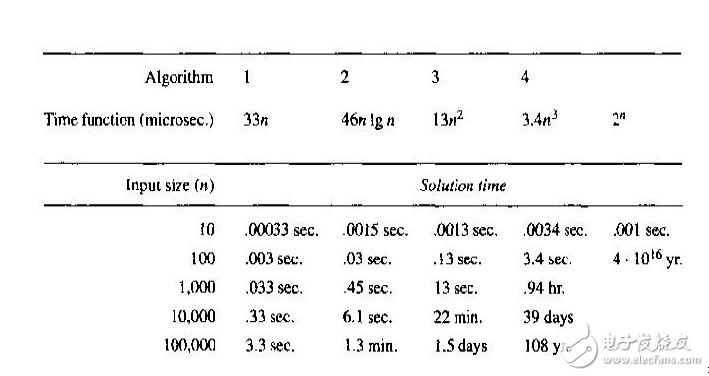
在上圖中,可以看到,當問題規模為10時,復雜度為O(3.4n^3) 的算法運行時間要0.0034s,復雜度為O(2^n) 的算法運行時間要0.001s,此時相差還不大,但當問題規模增加到100時,前者的運行時間只是增加到了3.4s,而后者的運行時間則增加到了4×10^16年!
因為實際問題的規模都比較大,100還是小數字,所以對一個問題,都努力尋求多項式算法。但也有問題目前還沒有找到多項式時間的精確算法,比如旅行商問題,因此就產生了各種近似算法,以解的質量來換取效率,尋求滿意解而不是最優解,蟻群算法就是其中一種。
所以,針對本問題的提法,蟻群算法和Prime 算法或Kruskal 算法等是兩個不同層面上的算法,基本沒有比較的必要,但可以做辨析:
1、Prime 算法,Kruskal 算法,Dijkstra 算法都只是解決某一種問題的,這些問題有了這些算法,就沒有必要使用蟻群算法。
2、蟻群算法可以用來解決一些尚未找到有效算法的問題,而且蟻群算法還是元啟發式算法(Metaheuristic),是一種算法框架,可以在其基本思想上針對不同問題做改進從而應用到不同問題上去。
3、蟻群算法可以和其它近似算法相比較,而這些算法本身也根據問題的不同有較大的改進彈性。
*圖片來源:Sara Baase, Allen Van Gelder,Computer Algorithms: Introduction to Design and Analysis,影印版第三版,高等教育出版社,2001 (第49頁 圖1.5)
 電子發燒友App
電子發燒友App






















評論