蟻群算法即相關代碼實現詳解
一.算法背景
蟻群算法是近年來剛剛誕生的隨機優化方法,它是一種源于大自然的新的仿生類算法.由意大利學者Dorigo最早提出,螞蟻算法主要是通過螞蟻群體之間的信息傳遞而達到尋優的目的,最初又稱蟻群優化方法(Ant Colony Optimization簡稱ACO).由于模擬仿真中使用了人工螞蟻的概念,因此亦稱螞蟻系統.
二.簡單說明
1)先看兩張圖
?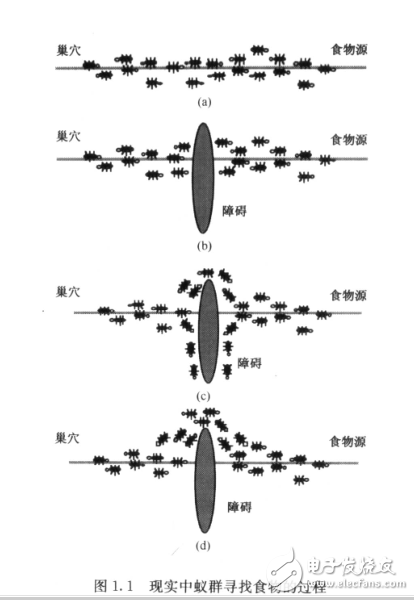
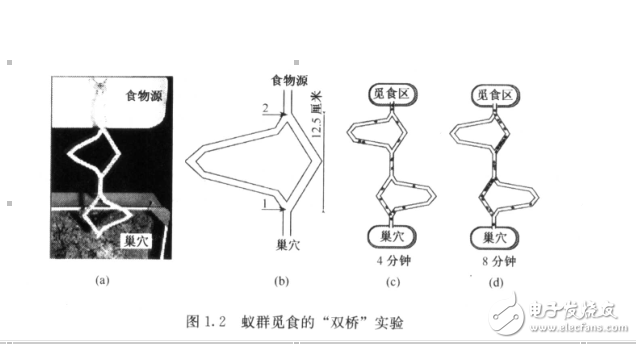
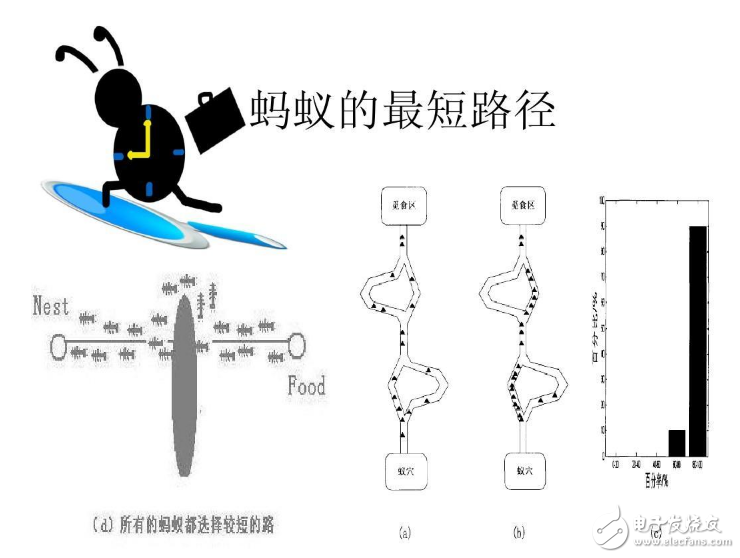
圖1-1顯示了螞蟻從巢穴出去覓食的過程,起初在遇到障礙的時候,會以相同的概率選擇通過障礙的路徑(即選擇了兩條路徑假設為路徑1和2,且每條路徑上的螞蟻數量是相同的).而在圖1-1(d)中,螞蟻們卻不再選擇路徑(2)),這就是蟻群算法的“雙橋模型”,這是什么原因呢?
2)算法探究
經過探究,上述的實驗反應了螞蟻在群體行為中的一種信息正反饋現象.螞蟻個體間通過這種信息交流機制來搜索食物.而用來交流反饋的化學因素現在被我們稱之為——————“信息素”.
然后建立相關“雙橋”實驗的數學模型,首先,假設在對稱橋的信息素的總數與過去一段時間內經過該橋的螞蟻數目成正比(即每只螞蟻都具有相同的信息素釋放能力);其次,假設某時刻螞蟻按照橋上殘留信息量的多少來選擇其中的某條路徑,經過該路徑的螞蟻數目越多,則該橋上的殘留信息素總量就越大.假設1-1圖中的兩條路徑分別為A和B,Am和Bm分別表示通過路徑A和B的螞蟻數目.則當所有M(Am+Bm=M)只螞蟻通過障礙后,第(M+1)只螞蟻選擇路徑A的概率為
??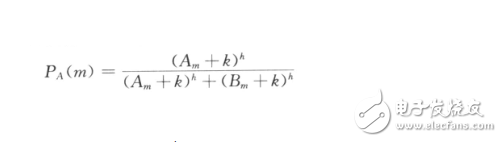
相反選擇路徑B的概率為
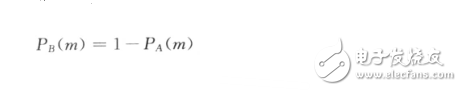
其中參數h(期望因子)和k(啟發因子)用來匹配真實實驗數據,第(M+1)只螞蟻按照上述公式計算概率,然后生成一個區間在[0,1]上均勻分布的隨機數w,若w<=P(A),則選擇路徑A,否則選擇路徑B.
三.matlab相關代碼實現(以TSP旅行商問題為例)
以下是解放軍信息工程大學一個老師編的matlab程序,網上有很多版本,已經由本人添加注釋并修改過請尊重原作者勞動,引用時請注明出處.
%符號說明
%SumOfant表示螞蟻數量
%SumOfCity表示城市數量
%sight為距離的倒數,表示每條邊的能見度
%Q表示信息素增強的系數
%nc_now表示當前的迭代次數
%nc_max表示自主設置的最大迭代次數 表示終止條件
%RouteOfBest表示各代的最佳路線
%LengthOfBest表示每次迭代的最佳路線的長度
%a表示啟發因子,表示信息素的相對重要程度
%b表示期望因子,表示能見度的重要性
%p表示信息素的蒸發系數,(1-p)表示信息素持久性系數
%length_address表示兩兩城市間的距離
for n=1:size(first_address)
for m=1:size(first_address)
length_address(n,m)=[(first_address(n,1)-first_address(m,1))^2+(first_address(n,2)-first_address(m,2))^2]^1/2;
end
end
sight=1./length_address;%表示每條邊的能見度
SumOfCity=20;
>> SumOfant=40;
>> sight=1./length_address;
info_pre=ones(SumOfCity,SumOfCity);
%info_pre為信息素矩陣,可以理解為在螞蟻還沒有被放入城市前,每條道路上就已經存在了一定含量的信息素(只是為了方便計算)
>> EachOfRoute=zeros(SumOfCity,SumOfCity);
> %存儲并記錄每次迭代時每只螞蟻經歷的路徑生成;
>> nc_now=1; nc_max=60; %迭代計數器,記錄迭代次數,此處設置為60次迭代
>> RouteOfBest=zeros(nc_max,SumOfCity); %各代最佳路線
Length_best=inf.*ones(nc_max,1); %各代最佳路線的長度
LengthOfAverage=zeros(nc_max,1); %各代路線的平均長度
while nc_now<=nc_max%表示循環終止條件,迭代終止器
%%第二步:將m只螞蟻放到n個城市上
Randpos=[]; %隨即存取
for i=1:(ceil(SumOfant/SumOfCity))
%ceil為取整函數,表示每個城市放幾只螞蟻
Randpos=[Randpos,randperm(SumOfCity)];
%randperm表示1-20隨機分配,也就是每只螞蟻的位置
end %表示每只螞蟻一開始所被放置的位置%第三步:所有螞蟻按概率函數選擇下一座城市,完成各自的周游
for j=2:SumOfCity %每只螞蟻從第一個城市出發,開始依次訪問
for i=1:SumOfant CityOfVisited=EachOfRoute(i,1:(j-1)); %記錄已訪問的城市,避免重復訪問
J=zeros(1,(SumOfCity-j+1)); %待訪問的城市
P=J;
%待訪問城市的選擇概率分布,用P表示
Jc=1;%記錄已經訪問的城市數目
for k=1:SumOfCity
if length(find(CityOfVisited==k))==0 %開始時置0
J(Jc)=k; Jc=Jc+1; %訪問的城市個數自加1
end
end
%下面計算待選城市的概率分布
for k=1:length(J)%對每只螞蟻還沒有訪問的城市依次計算概率
P(k)=(info_pre(CityOfVisited(end),J(k))^0.7)*(sight(CityOfVisited(end),J(k))^3.8);%在這里設置啟發因子=0.7,期望因子=3.8 end P=P/(sum(P));%按概率原則選取下一個城市
Pcum=cumsum(P); %cumsum,元素累加即求和
Select=find(Pcum>=rand); %若計算的概率大于原來的就選擇這條路線
CityOfNextVisit=J(Select(1));
EachOfRoute(i,j)=CityOfNextVisit;
end
end
if nc_now>=2
EachOfRoute(1,:)=RouteOfBest(nc_now-1,:);
%如果迭代次數大于2,則將前依次迭代的訪問順序存入EachOfRoute
end%%第四步:記錄本次迭代最佳路線
L=zeros(SumOfant,1); %開始距離為0,m*1的列向量
for i=1:SumOfant
R=EachOfRoute(i,:);
?


其中DrawRoute為自己寫的一個畫圖函數,推薦程序如下
?
 電子發燒友App
電子發燒友App
























評論