規則引導的知識圖譜聯合嵌入方法
人工智能技術與咨詢?
本文來自《計算機研究與發展》?,作者姚思雨等
摘 要?近年來,大量研究工作致力于知識圖譜的嵌入學習,旨在將知識圖譜中的實體與關系映射到低維連續的向量空間中.且所學習到的嵌入表示已被成功用于緩解大規模知識圖譜的計算效率低下問題.然而,大多數現有嵌入學習模型僅考慮知識圖譜的結構信息.知識圖譜中還包含有豐富的上下文信息和文本信息,它們也可被用于學習更準確的嵌入表示.針對這一問題,提出了一種規則引導的知識圖譜聯合嵌入學習模型,基于圖卷積網絡,將上下文信息與文本信息融合到實體與關系的嵌入表示中.特別是針對上下文信息的卷積編碼,通過計算單條上下文信息的置信度與關聯度來度量其重要程度.對于置信度,定義了一個簡單有效的規則并依據該規則進行計算.對于關聯度,提出了一種基于文本表示的計算方法.最后,在2個基準數據集上進行的實驗結果證明了模型的有效性.
關鍵詞?知識圖譜;表示學習;圖卷積網絡;上下文信息;文本信息
近年來,由于具有表達能力強、歧義性低、模式統一、且支持推理等優點,知識圖譜已被廣泛用于組織和發布各領域的結構化數據.通常,知識圖譜由實體、實體所具有的屬性以及實體間的關系所組成.例如,其中可能包含有實體中國、關系首都以及實體屬性“China”. 如圖1所示,知識圖譜的基礎構成則是描述2個實體之間的關系或實體及其屬性之間關系的三元組,如(中國,首都,北京)、(中國,英語標簽,“China”).
Fig. 1 Several triples which contain the entity Beijing and the related literals
圖1 包含實體“北京”的若干三元組及文本信息
目前,知識圖譜已被廣泛應用在智能問答[1]、推薦系統[2]和信息檢索[3]等任務中,其突出表現在學術與工業界均獲得了廣泛關注[4].但是,受益于知識圖譜所包含豐富信息的同時,其龐大的規模與數據稀疏性問題也給知識圖譜的應用帶來了挑戰.例如,Freebase[5], Yago[6]和Dbpedia[7]等開放領域知識圖譜中通常包含有數百萬個實體,以及上億條描述實體關系的三元組.將子圖匹配等傳統圖算法應用在這些大規模知識圖譜上往往存在計算低效性問題.為此,研究人員提出了知識圖譜嵌入學習模型(knowledge graph embedding learning model),將知識圖譜映射到低維、連續的向量空間中,學習實體與關系的嵌入表示[8].
通過設計特定的表示學習機制,知識圖譜的結構和語義等信息可被編碼在所學習到的嵌入表示中.一方面,原本需要對大規模知識圖譜進行頻繁訪問的操作,例如結構化查詢構建(structured query construction)[9]、邏輯查詢執行(logical query pro-cessing)[10]和查詢放縮(query relaxation)[11],均可在所學習到的嵌入表示空間中通過數值計算完成,極大地提高了效率.另一方面,知識圖譜的嵌入學習提供了一種抽取并高效表示知識圖譜特征信息的方法,類似于自然語言處理領域中被廣泛應用的詞嵌入(word embedding),知識圖譜的嵌入表示也為基于知識圖譜的深度學習工作提供了極大的便利.
現有知識圖譜嵌入學習模型大多僅關注知識圖譜中以三元組表示的結構信息.例如,Bordes等人提出了基于翻譯機制(translation mechanism)的TransE模型[12],其目標任務為鏈接預測(link prediction)與三元組分類(triple classification),概括而言就是判斷知識圖譜中給定的2個實體之間是否存在某個關系.因此TransE模型僅關注所學習到的嵌入表示對單條三元組結構信息的編碼,其在嵌入學習過程中將知識圖譜簡化為互不相關的三元組的有限集合.因此,TransE及其后續改進模型[13-16]對知識圖譜中上下文信息的編碼能力非常弱,很難應用于語義相關的任務.針對這一問題,相繼有一些基于上下文信息的嵌入表示模型被提出,如GAKE[17], RDF2Vec[18].但是它們仍然僅關注知識圖譜中由子圖、路徑等結構所表示的上下文信息.例如,在學習圖1中實體北京的嵌入表示時,上述方法僅關注(中國,首都,北京)與(北京,位于,華北)等描述實體間關系的三元組,而忽略了北京的簡介、英文標簽等文本信息.顯然,文本信息的缺失限制了所學到嵌入表示對語義信息的表達.
為解決這一問題,本文提出了一種規則引導的知識圖譜聯合嵌入學習模型.受Vashishth等人[19]所提出的圖卷積網絡啟發,模型首先通過多關系型圖卷積將實體在知識圖譜中的上下文信息編碼到實體的嵌入表示中.與Vashishth等人的工作所不同的是,本文認為實體的多條上下文信息應該具有不同的重要程度,并且某條上下文信息的重要程度取決于2個因素:該條上下文信息的置信度,以及其相對于實體的關聯度.為此,本文提出了一條簡單有效的規則引導上下文信息置信度的計算,并基于知識圖譜中的文本信息表示提出了實體與其上下文信息之間關聯度的計算方法.最后,模型將圖卷積網絡所編碼的嵌入表示與文本信息的向量表示整合,以鏈接預測任務的結果作為訓練目標,學習知識圖譜中實體與關系的嵌入表示.
本文貢獻主要體現在3個方面:
1) 基于圖卷積網絡,創新地提出了一種聯合考慮知識圖譜中上下文信息與文本信息,由規則引導的嵌入表示學習模型.
2) 針對上下文信息在圖卷積中的重要程度,提出了應用規則以及知識圖譜中文本信息來計算單條上下文信息置信度與關聯度的新方法.
3) 在基準數據集上進行了充分的實驗,并與相關的知識圖譜嵌入學習方法進行了對比,實驗結果驗證了本文模型的有效性.
1 相關工作
本節對與本文工作較相關的知識圖譜嵌入學習模型進行介紹,由于本文所提出的模型是基于圖神經網絡的,因此分別介紹基于圖神經網絡的知識圖譜嵌入學習模型和其他非圖神經網絡的嵌入學習模型.
1.1 基于圖神經網絡的模型
基于圖神經網絡的模型主要包括R-GCN[20], W-GCN[21], CompGCN[19]等.該類模型通常將圖卷積網絡作為編碼器,對圖結構數據進行編碼,并結合對應的解碼器進行知識圖譜上的鏈接預測、節點分類等任務.在R-GCN中,每層網絡中節點與關系的特征利用權重矩陣進行計算,并通過領域聚合的方式傳遞至后續網絡層.具體而言,R-GCN利用基分解和塊對角分解構造特定關系的權重矩陣,以處理不同類型的鄰居關系,將其與鄰居節點信息進行融合,并傳遞到目標實體上進行更新.W-GCN在圖卷積網絡聚合過程中為每個權重矩陣分配可學習的權重參數,使模型獲得更優的實體嵌入表示.CompGCN則提出了針對中心節點的領域信息聚合方法,在理論上使用多種“實體-關系”組合算法對當前主流的基于多關系的圖卷積網絡模型進行了概括.
1.2 非圖神經網絡的模型
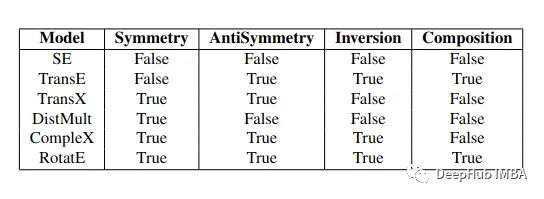
非圖神經網絡的嵌入學習模型類別較多,主要包括基于翻譯機制的模型,如TransE[12]及其后續改進模型,包括TransH[13],TransR[14],TransD[15],TransAH[16],基于上下文信息的模型,如GAKE[17],RDF2Vec[18],基于張量分解的模型,如ComplEx[22],RESCAL[23].
其中,基于翻譯機制的模型應用較為廣泛.該類模型通常僅關注知識圖譜的結構信息,將實體之間的關系表示為嵌入向量空間中的某種翻譯操作(translation operation).以TransE為例,其將知識圖譜中的實體與關系都表示在同一個低維歐幾里得空間中,以向量表示一個實體或關系.具體而言,對于知識圖譜中的一條三元組(h,r,t),TransE 將其中的關系r看作在歐幾里得空間中從頭實體h到尾實體t的平移操作,即其期望頭實體所對應的向量h經過關系所對應的向量r的平移操作后可以非常逼近尾實體所對應的向量t,即h+r≈t.
TransE的翻譯機制較為簡單,因此可以高效地應用于大規模知識圖譜,但同時又限制了其模型的表達能力,使其難以處理一對多、多對一以及多對多類型的復雜關系[14].為解決這一問題,TransE之后相繼有一些翻譯機制更加復雜的模型被提出.例如,TransH[15]相對于所給定三元組中關系的超平面空間設計翻譯機制,TransR[16]則針對知識圖譜中的每一個關系額外學習一個矩陣,借助該矩陣將頭、尾實體通過線性變換映射到相應的關系向量空間中,然后再計算其翻譯機制的損失值.
2 聯合嵌入表示學習
本節首先對知識圖譜嵌入學習問題進行形式化定義,介紹相關概念的符號表示,然后詳細介紹所提出的規則引導的聯合嵌入學習模型.
2.1 問題定義
本文將知識圖譜表示為
其中
分別代表知識圖譜中的實體與關系集合.對于某個三元組
其中頭尾實體均屬于實體集合,即
其中關系屬于關系集合,即
知識圖譜的嵌入學習問題在于學習給定知識圖譜
中任意實體
與任意關系
的向量表示e,r∈
d,其中為d嵌入表示的維度.本文通過鏈接預測任務評價所學習到的嵌入表示,該任務可能包括2種情形:給定實體
與關系
基于它們的嵌入表示e,r∈
d,預測另外一個實體
使得存在三元組
或
或者給定2個實體
基于它們的嵌入表示e,e′∈
d,預測一個關系
使得存在三元組
或
對于任意實體
與關系
本文將它們所對應的文本信息表示為le與lr.對于實體
本文將其所有鄰居三元組的集合
視為e的上下文,具體而言
為集合
與集合
的并集,且對于
中任意鄰居三元組,本文認為其表達了節點e的一條上下文信息.
與Vashishth等人[19]的做法類似,本文也對知識圖譜的關系集合進行擴充:
其中
為逆關系集合.具體而言,對于任意三元組
本文在關系集合中增加一條逆關系r-1,并相應地將三元組(et,r-1,eh)添加到知識圖譜
中,即
代表自環關系集合,即對于任意實體
在知識圖譜
中添加自環三元組,即
此外,本文使用
代表實體e周圍鄰居實體的集合,
代表實體e周圍鄰居關系的集合,例如對于圖1中的實體北京,其鄰居實體集合為{華北,中國,…},鄰居關系集合為{位于,首都,簡介,英文標簽,…}.
2.2 模型整體架構
本文基于知識圖譜的上下文信息與文本信息聯合學習實體與關系的嵌入表示.圖2展示了模型的整體架構,針對節點eh,其上下文信息
由包括三元組(eh,ri,eti)在內的所有鄰居三元組表達.本文模型利用圖卷積網絡,基于
將eh的上下文信息編碼到其嵌入表示中.并且,本文認為eh的不同鄰居三元組所各自表達的上下文信息具有不同的重要程度,通過計算單條上下文信息的置信度與關聯度對其重要程度進行度量.
對于置信度計算,本文針對上下文信息中所包含的關系提出一條簡單有效的規則,并基于該規則在嵌入學習之前預先計算特定于一對關系的置信度矩陣C,并在圖卷積過程中利用該矩陣計算某條上下文信息的置信度,如圖2中標有置信度計算的虛線所示.
Fig. 2 An overview of the core part of the model
圖2 模型核心部分框架圖
?
對于關聯度計算,本文首先利用預訓練語言模型對知識圖譜中實體與關系的文本信息進行編碼.如圖2所示,對于實體eh與關系ri的文本leh與lri,它們的文本向量分別記為Leh與Lri.本文基于實體與關系的文本向量表示計算單條上下文信息與其對應實體之間的關聯度,如圖2中標有關聯度計算的虛線所示.
值得一提的是,本文所提出的模型采用“編碼器-解碼器”框架(encoder-decoder).上述基于圖卷積網絡的上下文信息編碼即為編碼器的主要內容.除此之外,編碼器還將上述過程學習到的實體與關系的嵌入表示與它們的文本表示相結合.本文模型的解碼器則主要基于ConvE模型[24]實現.下面對模型的細節進行詳細的介紹.
2.3 編碼器
規則引導的置信度計算. 知識圖譜中的關系并非相互獨立.對于一個實體
當e擁有一條鄰居關系
時,這可能暗示其還同時擁有另一條鄰居關系
例如,當某個實體的一條鄰居關系為首都時,其很可能擁有另外一個鄰居關系市長.因為顯然只有城市才可能是“首都”,并且其往往擁有“市長”這一上下文信息.本文認為這種關系間的聯系可用于對上下文信息的置信度進行估算.因此,本文提出以下規則:對于實體
當其某條上下文信息中包含有關系
并且
中同時存在關系r2,r1≠r2.此時,對于知識圖譜中任意實體
出現
的概率越高,相對于e而言包含r1的上下文信息置信度越高.例如,當某個實體擁有一條包含有關系市長的上下文信息時,如果該實體同時擁有關系首都,那么包含有市長的上下文信息置信度較高,因為首都與市長通常同時出現在實體的上下文中.
基于上述規則,本文在進行圖卷積網絡的訓練前首先計算置信度矩陣C∈
表示集合的大小.對于矩陣中的任意參數Ci,j,0≤i,j≤
其計算如下:
(1)
其中,分母表示知識圖譜中擁有鄰居關系ri的實體的個數,分子表示同時擁有鄰居關系ri與rj的實體的個數,i與j在此表示關系ri與rj在關系集合
中的索引.
對于圖2中實體eh,當利用其鄰居三元組
通過圖卷積編碼其向量表示eh時,模型會首先基于置信度矩陣C評價eh的各個鄰居三元組.例如,圖2中鄰居三元組(eh,ri,eti)的置信度可以通過式(2)來計算:
(2)
其中,
代表實體eti鄰居關系集合,id(·)表示關系在
中的索引.值得一提的是,在本文模型的實現中,置信度計算被整合到了關聯度計算中對其進行詳細介紹.
基于文本信息的關聯度計算.考慮到知識圖譜中實體與其不同上下文信息之間關聯度的差異,在進行實體嵌入表示的卷積編碼時,關聯度高的上下文信息應該獲得更多的關注.為此,本文借助實體和關系的文本描述作為輔助信息計算實體與其單條上下文信息之間的關聯度,用于后續圖卷積網絡中實體嵌入表示的更新.本文首先將知識圖譜中實體和關系的文本描述輸入到預訓練的BERT[25]語言模型中,得到它們所對應的初始文本表示,然后再分別利用實體文本轉換矩陣與關系文本轉換矩陣計算它們的最終文本表示.具體而言,對于任意實體
與關系
其對應文本分別為le與lr,它們通過BERT得到的初始文本表示為
與
轉換后的最終文本表示為Le與Lr,其中
本文利用實體與關系的文本表示計算對于某一實體而言,其單條上下文信息的關聯度.如圖2所示,實體eh的一條鄰居三元組為(eh,ri,eti),本文計算參數βi與γi來度量該條鄰居三元組所表示的上下文信息與eh之間的關聯度,具體公式為:
(3)
其中,Lej與Leh分別為實體ej與eh的文本表示,
為實體eti的鄰居實體集合.
(4)
其中,Lrj與Lri分別為關系rj與ri的文本表示,
為實體eti的鄰居關系集合,Cid(ri),id(rj)如式(2)所定義.
基于圖卷積網絡的嵌入更新.本文采用Vashishth等人所提出的CompGCN[19]模型作為圖卷積網絡的架構,對知識圖譜上下文信息進行編碼.
初始狀態下,對于任意實體
與關系
其嵌入表示為隨機向量e0與r0,且e0,r0∈
d.以圖2中的實體eh為例,其嵌入表示通過以下圖卷積過程進行更新:
(5)
其中,
表示實體eh的鄰居三元組集合,
或
針對包含有鄰居關系ri與鄰居節點eti的一條上下文信息,αi基于置信度計算與關聯度計算度量該條上下文信息的重要程度,具體如下:
αi=λ1βi+λ2γi,
(6)
其中,βi由式(3)計算得到,γi則由式(4)計算得到;Wt(ri)為CompGCN[19]中定義的關系類別矩陣,由于知識圖譜中被加入了逆關系與自環關系,Wt(ri)∈
d′×d可能為3種不同的表示,具體為:
(7)
其中函數f(·)表示循環關聯操作(circular correla-tion)[26],可以將2個向量x,y∈
d進行融合,得到x°y∈
d,每個維度的數值計算為
(8)
遵循CompGCN框架,在對實體進行圖卷積編碼的同時,本文通過轉換矩陣Wr∈
d′×d更新關系的嵌入表示:
(9)
最后,本文將任意實體
與關系
的文本表示加入到其嵌入表示中,具體為:
e=e+Le,
(10)
r=r+Lr.
(11)
2.4 解碼器
本文采用ConvE[24]模型作為解碼器,基于所學習到的嵌入表示進行鏈接預測,通過提高鏈接預測的表現更新模型參數.當知識圖譜經過編碼器編碼后,對于某個任意構成的三元組(eh,r,et),可知其頭尾實體eh與et的嵌入表示為eh與et,關系r的嵌入表示為r.ConvE模型首先將eh與r轉換成二維形式,即
與
然后計算該三元組的分數值:
sc(eh,r,et)=
?
(12)
其中,[·]表示相連接,ω表示卷積過濾器,vec(·)為ConvE所定義的維度變換,Wcov為參數矩陣,f′(·)為非線性函數.當式(12)計算得到的分數值越高,(eh,r,et)越有可能是正確的三元組.
3 實 驗
本節首先對實驗所使用的數據集、對比模型和評價指標等進行說明,然后介紹本文所提模型的實驗結果,并與其他基準模型進行比較與分析.
3.1 數據集及對比模型介紹
本文在2個廣泛使用的數據集上進行試驗,分別是FB15K-237[27]和WN18[12],其統計數據如表1所示:
Table 1 Summary Statistics of Knowledge Graphs
表1 數據集的統計信息
為驗證所提模型的有效性,本文廣泛選取了當前被應用較多的知識圖譜嵌入學習模型作為對比方法,具體包括TransE[11],DistMult[28],ComplEx[22],R-GCN[20],KBGAN[29],ConvE[24],ConvKB[30],SACN[21],HypER[31],RotatE[32],ConvR[33],VR-GCN[34],CompGCN[19].其中,TransE[11]為基于翻譯機制的嵌入學習模型,上文已對其進行了詳細介紹.DistMult[28]將實體表示為通過神經網絡學習到的低維向量,將關系表示為雙線性或線性映射函數.ComplEx[22]與RESCAL[23]模型類似,屬于基于矩陣/張量分解進行鏈接預測的模型.R-GCN[20],VR-GCN[34]與CompGCN[19]屬于基于圖卷積網絡的嵌入表示模型,以R-GCN[20]為例,其將知識圖譜中的關系編碼為矩陣,通過關系矩陣傳遞相鄰實體的嵌入信息,并采用了多層圖卷積網絡.KBGAN則應用了對抗生成網絡(generative adversarial network, GAN),在訓練過程中生成更具迷惑性的負例來提高嵌入表示的訓練效果.本文應用了ConvE[24]模型作為解碼器,在第2節中對其進行了詳細介紹.ConvKB[30],ConvR[33],SACN[21]與HypER[31]均是基于卷積神經網絡的方法.以HypER[31]為例,其可以生成簡化的與關系相關的卷積過濾器,且可被構造為張量分解.RotatE[32]與TransE[11]等基于翻譯機制的模型類似,其將實體之間的關系表示為向量空間中從頭實體到尾實體的旋轉.
3.2 評價方法說明
本文通過鏈接預測任務來對模型的有效性進行評價.在實驗中,針對被事先去掉頭實體或尾實體的測試三元組,本文基于學習到的嵌入表示推測其被去掉的頭實體或尾實體.具體對于每個測試三元組,本文選取知識圖譜中的任意實體作為可能的預測結果,并計算利用該實體補全測試三元組后的分數值,如式(12)所示,最后對分數值進行排序.在此以缺失頭實體的預測為例,對于測試集中每個三元組(eh,r,et),事先刪除其頭實體eh,然后試圖使用G中的任意實體
補齊該測試三元組,從而產生候選三元組集合
最后,基于所學習到的嵌入表示計算候選三元組的分數值并進行排序,分數值越高表明學習到的模型,即嵌入表示,認為該結果更可靠,通過與真實結果進行比較從而判段所學習嵌入表示的優劣.
最后采用MR(mean rank),MRR(mean reciprocal rank)和Hit@k作為評價指標[12].其中,MR與MRR均為預測結果平均排名的指標,Hit@k則指預測結果排在前k名中的比例,本文具體采用Hit@10,Hit@3和Hit@1.總之,越好的預測結果,其MR值越低、MRR值越高、Hit@k也越高.
3.3 實驗設置
本文實驗代碼使用Python實現,在配置Ubuntu 16.04.6 LTS操作系統的服務器上完成,其CPU配置為16核Intel Core i7-6900K 3.20 GHz, 內存128 GB,GPU配置為4張GeForce GTX 1080 GPU卡.
對于實體和關系文本表示向量的編碼,本文借助pretrained-bert-base-uncased預訓練模型(1)https://github.com/google-research/bert,文本向量初始維度為768,轉換后的維度為200.在圖卷積網絡中,實體和關系的初始化向量維度為100,即d=100,GCN的維度為200,即d′=200.解碼器中維度轉換的高度和寬度分別為10和20,卷積過濾器的大小為7×7,數量為200.利用Adam優化器對整體模型進行訓練,批大小(batch size)為256,學習率(learning rate)為0.001.
本文對TransE模型進行了復現,其余模型則引用對比模型論文中所報告的結果.
3.4 實驗結果分析
表2報告了本文模型與對比模型在鏈接預測任務中的實驗結果.
通過表2可觀察到如下結果:
1) 本文模型在各個評價指標上顯著優于TransE,DistMult和ComplEx等基準模型,與SACN,HypER和CompGCN等最新提出的模型十分接近,由此可證明本文模型的有效性.對于FB15K-237數據集,本文在Hit@10指標上排名第一.
2) 在Hit@1和Hit@3指標上也與CompGCN,ConvR,SACN相差極小.具體在Hit@1指標上僅比最高的CompGCN低1.51%,在MRR指標上與CompGCN相比僅低0.8%.而對于WN18數據集,本文模型在MR指標上排名第一,在Hit@10和Hit@3指標上也與第一名差距微小.具體在Hit@10指標上比RotatE低0.2%,在Hit@3指標上比ConvR和HypER僅低0.9%.
3) 基于圖神經網絡的嵌入學習方法的表現普遍優于TransE等僅關注結構化信息的模型.就本文模型而言,由于其基于圖卷積網絡對知識圖譜的上下文信息與文本信息進行了聯合嵌入表示,顯著提高了在鏈接預測任務中的表現.
Table 2 Link Prediction Results on FB15K-237 and WN18
表2 鏈接預測在FB15K-237和WN18上的結果
Note: The best performance is in bold.
?
4 總 結
現有多數知識圖譜嵌入學習方法僅考慮由三元組表示的知識圖譜結構信息,而忽視了知識圖譜中豐富的上下文信息與文本信息,限制了嵌入表示在鏈接預測等任務中的表現.針對現有方法的這一局限性,本文提出一種利用圖卷積神經網絡,結合知識圖譜的上下文信息與文本信息學習嵌入表示的方法.為了對上下文信息的重要程度進行細粒度分析,本文提出一條簡單有效的規則來計算上下文信息的置信度,并基于文本信息的向量表示提出計算上下文信息關聯度的方法,加強了對上下文信息的約束和引導.最后,通過在2個廣泛使用的基準數據集上進行對比實驗,驗證了本文模型的有效性.
關注微信公眾號:人工智能技術與咨詢。了解更多咨詢!
審核編輯:符乾江
 電子發燒友App
電子發燒友App





































評論