圖靈計(jì)算機(jī)是基于液冷GPU服務(wù)器、大數(shù)據(jù)一體機(jī)等技術(shù)，應(yīng)用于大數(shù)據(jù)、人工智能、元宇宙等領(lǐng)域。

在哥德爾研究成果的影響下，二十世紀(jì)三十年代后期圖靈從計(jì)算一個(gè)數(shù)的一般過程入手對計(jì)算的本質(zhì)進(jìn)行研究，從而實(shí)現(xiàn)對計(jì)算本質(zhì)的真正認(rèn)識(shí)。該成果不僅再次表明某些數(shù)學(xué)問題是不能用任何機(jī)械過程來解決的思想而且還深刻揭示計(jì)算所具有的能行過程的本質(zhì)特征。描述的是關(guān)于數(shù)值計(jì)算知道英文字母表的字母以及漢字均可以用數(shù)來表示，計(jì)算的每一過程都可以用字符串的形式進(jìn)行編碼，并存放在存儲(chǔ)器中，以后使用時(shí)譯碼并由處理器執(zhí)行。

圖靈可計(jì)算理論和人工智能現(xiàn)狀

可計(jì)算理論起源于1930，貢獻(xiàn)者包含圖靈、邱奇、哥德爾等。其中哥德爾的理論被稱為哥德爾不完備定理，邱奇和圖靈的理論合稱邱奇-圖靈論題。這些成果形成現(xiàn)代的圖靈可計(jì)算概念。

圖靈機(jī)是一種標(biāo)準(zhǔn)的計(jì)算模型。任何可計(jì)算問題，都可以通過圖靈機(jī)來進(jìn)行計(jì)算。不可計(jì)算數(shù)，或者叫做超越數(shù)，就是圖靈機(jī)無法計(jì)算的數(shù)。

現(xiàn)代計(jì)算機(jī)的計(jì)算模型其實(shí)就是一種通用圖靈機(jī)，Stephen Wolfram的110號元胞自動(dòng)機(jī)，也等價(jià)于通用圖靈機(jī)。

計(jì)算

越接近現(xiàn)代，計(jì)算就顯得越重要。

算力不只是可以挖點(diǎn)比特幣，也不是游戲或者英雄電影。

新的科技發(fā)展是充分模型的能力和計(jì)算的優(yōu)勢。模擬可以類比為科學(xué)，而擬真可以類比為技術(shù)。科學(xué)應(yīng)用于技術(shù)，可以類比于使用計(jì)算模擬以了解其工作原理，然后擬真到真實(shí)世界，以替代現(xiàn)有的其他功能。

如果有人告訴你，計(jì)算機(jī)無論多快，部署的計(jì)算無論有多多，其實(shí)它的計(jì)算是有極限的呢？

這其實(shí)就是人工智能的奠基者，圖靈的工作。

人工智能越是發(fā)展，越需要回歸圖靈。

不可判定、不完備不可計(jì)算及其比較分析

不可判定

一個(gè)圖靈機(jī)輸入一個(gè)字符串之后，可能進(jìn)入3種狀態(tài)：接受、拒絕、循環(huán)（即不停機(jī)）。對于一種語言A，其中任意字符串ω，總能設(shè)計(jì)一個(gè)圖靈機(jī)M，將ω輸入M后，M進(jìn)入接受狀態(tài)，并停機(jī)。圖靈機(jī)由有限的字符編碼而成，任何一臺(tái)圖靈機(jī)均可表述為一個(gè)字符串。比如圖靈機(jī)M，其字符串為，它描寫一個(gè)圖靈機(jī)。可以看作程序，ω就是輸入。有通用圖靈機(jī)U，可以模擬圖靈機(jī)M，從中解析出M的行為，并模擬出輸入ω的動(dòng)作，產(chǎn)生一樣的結(jié)果：接受、拒絕、循環(huán)。我們稱U接受。

不完備

與圖靈機(jī)一樣，哥德爾將形式邏輯也符號化，一個(gè)命題可以寫成一個(gè)形式化語言符號的形式，就是公式組成的字符串序列。并給每一個(gè)符號指定一個(gè)數(shù)字，把它作為質(zhì)數(shù)的指數(shù)，將每一個(gè)字符串轉(zhuǎn)換為一個(gè)自然數(shù)，即哥德爾數(shù)。這樣，就將可證轉(zhuǎn)換為算術(shù)問題。

不可計(jì)算

邱奇、圖靈和哥德爾等的理論引入之后，我們漸漸開始將實(shí)數(shù)和不可計(jì)算聯(lián)系起來。哥德爾不完備定理可以表示為，存在一些實(shí)數(shù)，是不可計(jì)算的。可計(jì)算數(shù)被定義為，一個(gè)實(shí)數(shù)可以通過圖靈機(jī)通過有限的算法得到。比如e、π、方根。原則上，可以表示為連分?jǐn)?shù)的數(shù)，都可以由圖靈機(jī)進(jìn)行計(jì)算。在可計(jì)算數(shù)之外，仍然存在一些不可計(jì)算的函數(shù)。或者說，存在一些實(shí)數(shù)，不能通過圖靈機(jī)有限的算法得到。

元胞自動(dòng)機(jī)

元胞自動(dòng)機(jī)CA是一種多維格點(diǎn)，常用的是二維格點(diǎn)由顏色確定，黑或者白，代表0或者1。每個(gè)格點(diǎn)由臨近的格點(diǎn)位置狀態(tài)決定，即局域規(guī)則。通過計(jì)算步驟（即離散時(shí)間）的更新格點(diǎn)狀態(tài)。參考Conway的人生游戲。如果研究CA與其他系統(tǒng)的類比特性，可以約定一種停機(jī)條件，即達(dá)到某種吸引子為接受，達(dá)到某種吸引子的補(bǔ)集為拒絕，否則為循環(huán)運(yùn)行，精確定義參考Sutner。通用元胞自動(dòng)機(jī)，比如110號，參考Cook。這樣，一個(gè)元胞自動(dòng)機(jī)，可以由四種設(shè)置組成，值域A、維數(shù)d、局域規(guī)則φ，停機(jī)條件π。通用元胞自動(dòng)機(jī)U是能模擬其他元胞自動(dòng)機(jī)的行為。

比較分析

對形式系統(tǒng)、圖靈機(jī)、可計(jì)算、元胞自動(dòng)機(jī)等進(jìn)行比較分析。

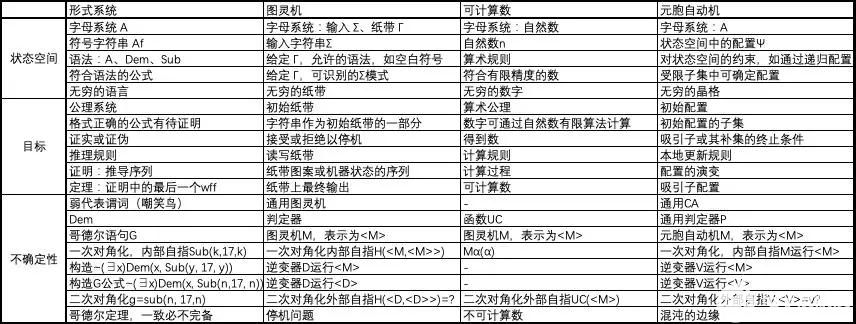
可以得出，不確定性的來源包含三個(gè)基本因素

一、程序數(shù)據(jù)的二元性；

二、必須有一個(gè)可數(shù)無窮；

三、是否運(yùn)算。

S. M. Markose也曾總結(jié)出三原則

一、代理可以對編碼信息、儲(chǔ)存的編碼代碼進(jìn)行操作；

二、代理可以進(jìn)行自指的離線模擬；

三、代理可以記錄否定，可自行參考。

但這里涉及的自指和無窮的問題還需要仔細(xì)進(jìn)行澄清。

拓?fù)淇捎?jì)算

可計(jì)算數(shù)只是簡單的把數(shù)分為了可計(jì)算數(shù)和不可計(jì)算數(shù)，但不可計(jì)算數(shù)實(shí)際上還可以深入考察。將圖靈可計(jì)算概念做一個(gè)簡單的擴(kuò)展，稱為拓?fù)淇捎?jì)算。

π是一個(gè)可計(jì)算數(shù)，雖然它是無窮的，它的勢為?0，即可數(shù)無窮，等勢于自然數(shù)，我們稱它拓?fù)淇捎?jì)算值為0（類比于球面）。實(shí)數(shù)中無理數(shù)之上的不可計(jì)算數(shù)，它的勢為?1，我們稱它拓?fù)淇捎?jì)算值為1（類比于環(huán)面的洞）。依次類推，?n的拓?fù)淇捎?jì)算值為n。

為什么所有整數(shù)、有理數(shù)都是可計(jì)算的？為什么π是可計(jì)算的？因?yàn)棣锌梢员硎緸檫B分?jǐn)?shù)的形式，即自然數(shù)的無窮次計(jì)算。可能是因?yàn)橹挥幸粋€(gè)可數(shù)無窮。所以，在圖靈機(jī)中就是可計(jì)算的。如果在圖靈機(jī)中再引入一個(gè)無窮，比如可數(shù)無窮狀態(tài)的圖靈機(jī)，那么拓?fù)淇捎?jì)算值為1的實(shí)數(shù)可能也是可計(jì)算的。這樣，拓?fù)淇捎?jì)算值為n的數(shù)，就可以用引入n個(gè)可數(shù)無窮的圖靈機(jī)來計(jì)算。

我們稱這種圖靈機(jī)為拓?fù)鋱D靈機(jī)。傳統(tǒng)的有限狀態(tài)圖靈機(jī)即0值拓?fù)鋱D靈機(jī)。可數(shù)無窮狀態(tài)圖靈機(jī)即1值拓?fù)鋱D靈機(jī)。

有意思的是，如果認(rèn)為自指與無窮等價(jià)（圖靈機(jī)中引入自指和引入可數(shù)無窮等價(jià)）。那么，在圖靈機(jī)中引入一個(gè)自指，相當(dāng)于引入一個(gè)無窮。自指有限狀態(tài)圖靈機(jī)相當(dāng)于1值拓?fù)鋱D靈機(jī)，1值圖靈機(jī)可以計(jì)算拓?fù)淇捎?jì)算值為1的實(shí)數(shù)。自指無限狀態(tài)圖靈機(jī)，就是2值拓?fù)鋱D靈機(jī)，可以計(jì)算實(shí)數(shù)函數(shù)、可數(shù)無窮維點(diǎn)集、不可導(dǎo)曲線集這些勢為?2的集合中的元素。

復(fù)雜計(jì)算

無窮∞，總是一個(gè)讓人難以割舍的概念。這里可以再做一個(gè)簡單的擴(kuò)展，試著將它從基本假設(shè)中排除掉。

考慮到圖靈可計(jì)算概念包含一個(gè)可數(shù)無窮，可以引入一個(gè)足夠大的數(shù)字n，將圖靈機(jī)的無窮限制在n之內(nèi)。但可以保留自然數(shù)集和實(shí)數(shù)集之間的關(guān)系，或者說?0、?1之間的關(guān)系，冪集關(guān)系。這樣，實(shí)數(shù)集對圖靈機(jī)不可計(jì)算。等價(jià)為?1的集合，對?0來說，不可計(jì)算。等價(jià)于，2^∞對于∞，不可計(jì)算。我們將∞換成n，即對于一個(gè)足夠大的數(shù)n，2^n對于n來說，不可計(jì)算。

這也重新定義一個(gè)“復(fù)雜”，即冪集2^n的系統(tǒng)，對于n的系統(tǒng)，是復(fù)雜的。而且，它就是不可計(jì)算，就是隨機(jī)。

注意到，自指產(chǎn)生一個(gè)復(fù)雜系統(tǒng)。

這樣，就對拓?fù)淇捎?jì)算概念做一個(gè)簡單的擴(kuò)展，可以稱為拓?fù)鋸?fù)雜可計(jì)算，或者簡稱復(fù)雜計(jì)算。

不妨將這種“復(fù)雜”直接定義為無窮（系統(tǒng)中，引入自指就是引入無窮，它引入一個(gè)冪集，產(chǎn)生不可判定），之前所知的“無窮”“∞”概念，不過是對于復(fù)雜度高于我們的世界的直覺而已。

從圖靈計(jì)算到量子計(jì)算

圖靈機(jī)包含目前的計(jì)算機(jī)的三個(gè)基本單元：存儲(chǔ)器、讀寫單元、控制單元。存儲(chǔ)器用以存儲(chǔ)信息，讀寫單元用以在存儲(chǔ)器中讀取或者寫入信息，而控制單元根據(jù)讀寫單元提供的信息按照內(nèi)部邏輯更改或刪除原有的信息，以達(dá)到我們期望的計(jì)算結(jié)果。

例如，在圖靈機(jī)執(zhí)行運(yùn)算時(shí)按照以下步驟依次進(jìn)行：

一、讀寫首先從儲(chǔ)存器獲取存儲(chǔ)信息，并將此信息傳遞到控制單元。

二、控制單元按照既定算法更改自身的狀態(tài)以及輸出新的數(shù)值到讀寫單元中。

三、讀寫單元向儲(chǔ)存器的當(dāng)前位置寫入新的值。

四、控制單元按照算法決定移動(dòng)方向，并進(jìn)行下一輪的讀寫。

下面我們嘗試使用一進(jìn)制加法說明這一工作過程。

在一進(jìn)制中，空=b，1=1，2=11，3=111。嘗試計(jì)算2+3的結(jié)果。控制器按照下面這個(gè)邏輯進(jìn)行操作：

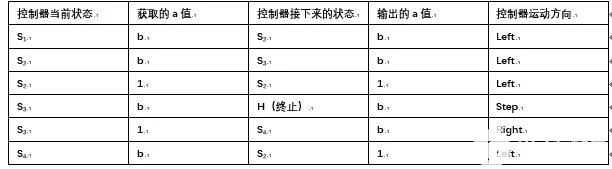
此時(shí)我們使用讀取單元讀取儲(chǔ)存器中記錄的數(shù)據(jù)為：

按照以上的邏輯，當(dāng)控制單元獲取不同a值時(shí)，將會(huì)改變自身的狀態(tài)并執(zhí)行相應(yīng)操作。例如開始時(shí)，控制單元狀態(tài)為S1讀取了b，控制器狀態(tài)轉(zhuǎn)變?yōu)镾2，并輸出b，隨后向左移動(dòng)一格，以此類推，不斷讀取并變換狀態(tài)完成整個(gè)加法運(yùn)算。

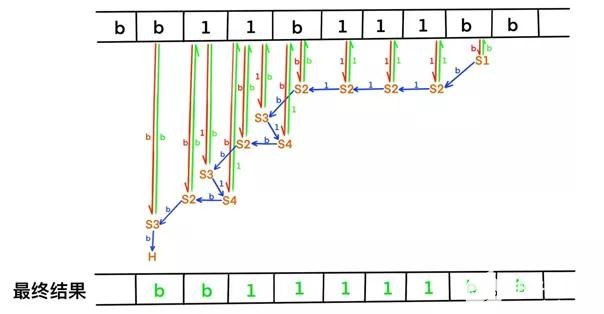
量子計(jì)算

自人類踏入到量子領(lǐng)域，找到一條使用粒子狀態(tài)作為計(jì)算的方法。一次量子計(jì)算由制備輸入態(tài)、對于初態(tài)執(zhí)行所期望的變換、測量輸出態(tài)這三個(gè)步驟組成。對應(yīng)于比特，我們在量子計(jì)算中稱這個(gè)記載信息的基本單位為量子比特。我們可以采用電子、核子、光子等等作為量子比特的載體。規(guī)定一對正交的量子態(tài)分別代表經(jīng)典比特的0與1，這對量子態(tài)構(gòu)成了量子計(jì)算的基矢。因此，相比于傳統(tǒng)計(jì)算機(jī)輸入僅可以是0或1的初值不同，量子力學(xué)的疊加原理允許量子計(jì)算輸入的初始態(tài)可以是疊加的。

量子比特所描繪的不再是單一的0或者1，而是一個(gè)以|0>與|1>為基失并由連續(xù)變量與描述的空間。由于信息載體的變化，發(fā)生的信息載體所承載的信息量由點(diǎn)向面變化。輸入的初始態(tài)就擁有著大量的信息。這樣的一個(gè)輸入態(tài)描繪了一部分態(tài)與一部分態(tài)的混合狀態(tài)，所以它既可以進(jìn)行態(tài)的相關(guān)運(yùn)算，也可以參與態(tài)的相關(guān)運(yùn)算。這種不同于傳統(tǒng)計(jì)算的模式，使得量子計(jì)算的過程是并行的（是尤為重要的），這就導(dǎo)致量子計(jì)算在一些特定問題上有著傳統(tǒng)計(jì)算模式（目前算法下）難以匹敵的計(jì)算能力。

這種并行計(jì)算所帶來的優(yōu)勢隨著量子比特的數(shù)目增多變得尤為明顯。假設(shè)我們都采用n個(gè)信息單位作為載體用以描述可能的狀態(tài)。對于經(jīng)典計(jì)算機(jī)而言，可以表示的狀態(tài)數(shù)目將會(huì)以模式增長。因此，兩者之間的差距在隨著n的增大而快速拉大。

走出實(shí)驗(yàn)室，賦能特色產(chǎn)業(yè)

如今量子計(jì)算所處的發(fā)展階段，有點(diǎn)類似于2012年的人工智能產(chǎn)業(yè)。2019年，谷歌演示了量子霸權(quán)，即在理論上越過了傳統(tǒng)算力，而在實(shí)踐上，行業(yè)正處于產(chǎn)業(yè)化爆發(fā)的前夜。

實(shí)驗(yàn)室里的理論再牛，也需要落地開花，而走出實(shí)驗(yàn)室，這場比拼已經(jīng)開始。圖靈量子完成1億元天使輪融資，而在美國和加拿大，PsiQ和Xanadu同期拿到了量子計(jì)算領(lǐng)域最大的兩筆投資。業(yè)內(nèi)人士甚至認(rèn)為，2021年可稱為光量子計(jì)算元年，上述三家行業(yè)最頂尖的公司，將決定更為廣泛的應(yīng)用走向。

?

《道德經(jīng)》有言：挫其銳，解其紛，和其光，同其塵。前沿科技特別是顛覆性技術(shù)，在發(fā)展道路上會(huì)遇到一些挫折和障礙，但既然選擇了這條道路，就要把阻力轉(zhuǎn)化為動(dòng)力，一旦實(shí)現(xiàn)顛覆性創(chuàng)新，回報(bào)必然是豐厚的。在上海創(chuàng)業(yè)的圖靈量子已定下最早應(yīng)用的方向——金融科技、生物醫(yī)藥、人工智能，這些是最需要算力算法支撐的行業(yè)，同時(shí)也最貼近上海的產(chǎn)業(yè)特色，可實(shí)現(xiàn)“上海賦能上海”的疊加效應(yīng)。

圖靈量子已與上海頂級三甲醫(yī)院、藥企巨頭、云計(jì)算服務(wù)商、金融機(jī)構(gòu)等戰(zhàn)略合作，通過量子計(jì)算來解決一類實(shí)用問題，真正賦能一個(gè)行業(yè)。在金賢敏看來，未來量子計(jì)算還可在智慧城市、大數(shù)據(jù)等需要復(fù)雜算法、算力的領(lǐng)域發(fā)揮優(yōu)勢。

《上海市戰(zhàn)略性新興產(chǎn)業(yè)和先導(dǎo)產(chǎn)業(yè)發(fā)展“十四五”規(guī)劃》提出，要形成“9+X”戰(zhàn)略性新興產(chǎn)業(yè)和先導(dǎo)產(chǎn)業(yè)發(fā)展體系，“重點(diǎn)布局光子芯片與器件”就是X之一。

藍(lán)海大腦大數(shù)據(jù)一體機(jī)

超能運(yùn)算

支持主流?GPU 顯卡虛擬化，提高計(jì)算性能和圖像渲染能力

快速實(shí)現(xiàn)系統(tǒng)擴(kuò)展，支持大規(guī)模并發(fā)運(yùn)行（百萬個(gè)理論節(jié)點(diǎn)）

高效運(yùn)維

一站式部署，開箱即用，助力企業(yè)快速實(shí)現(xiàn)業(yè)務(wù)轉(zhuǎn)型

強(qiáng)大的數(shù)據(jù)、網(wǎng)絡(luò)、虛擬化及管理安全保障，提高系統(tǒng)可靠性和高可用性

?

-END-

審核編輯：符乾江