今天給大俠帶來在畢業設計之基于FPGA的FIR數字濾波器設計,僅供大俠參考,話不多說,上貨。
本篇介紹基于FPGA的FIR數字濾波器設計,針對畢業設計要做的基本工作有如下幾點:
(一)掌握有限沖擊響應FIR(Finite Impulse Response, FIR)的基本結構,研究現有的實現方法,對各種方案和步驟進行比較和論證分析,然后針對目前FIR數字濾波器需要的特點,速度快和硬件規模小,作為指導思想進行設計計算。
(二)基于硬件FPGA的特點,利用Matlab軟件以及窗函數法設計濾波器。對整個FPGA元件,計劃采用模塊化、層次化設計思想,從而對各個部分功能進行更為詳細的理解和分工設計,最終FIR數字濾波器的設計語言選擇 Verilog HDL硬件編程語言。
(三)設計中的軟件仿真使用開發軟件Quartus II,并且利用Matlab工具進行對比仿真,在仿真的過程中,對比證明,本設計的濾波器的技術指標已經全部達標。
1.1 本課題研究意義
在現代通信信號處理領域中,隨著各種精密計算和快速計算的發展對信號處理的實時性、快速性的要求越來越高。以往的模擬濾波器無法克服電壓漂移、溫度漂移和噪聲等問題,從而帶來了許多誤差和不穩定因素。而數字濾波器具有穩定性高、精度高、設計靈活、實現方便等突出優點。
FPGA元器件在高速并行處理和數據傳輸中有獨特優勢,FPGA正在前端信號處理中越來越多地代替ASIC和DSP。我們需要的就是這種設計周期短,功能密度高,重組時間短的元器件。本文在FPGA元器件的基礎上,實現現代FIR數字濾波器功能。并且研究多種快速的FIR數字濾波器的理論設計思想和程序設計方法。
1.2 國內外研究現狀分析
1985年,Xilinx生產出了第一塊FPGA元器件,由于它有著集成度高、方便易用、開發和上市周期短的絕對優勢,使得FPGA器件在數字設計和電子生產中得到迅速普及和應用,發展潛力十分巨大。現在FPGA已經發展到可以利用硬件乘加器、片內儲存器、邏輯單元、流水處理技術等特有的硬件結構,高速完成FFT 、FIR 、復數乘加、卷積、三角函數以及矩陣運算等數字信號處理。這樣可以完成信號處理的主要技術,如中頻采樣、參數估計、自適應濾波、脈沖壓縮、自適應波束形成和旁瓣對消等。
1.3 研究思路
通過對目前數字濾波器的幾種實現方法的簡單分析,本文認為基于FPGA的數字濾波器具有許多優點,本文考慮到信息技術的發展對于數字濾波器的要求越來越高,而目前FIR數字濾波器的性能還不完善,于是選擇了基于FPGA的數字濾波器作為主要研究內容,通常濾波器在進行數據處理時用到了卷積運算,在設計中的解決這些乘法運算的思路是將它們轉換成加減法,這是目前解決乘法運算的主流思想。設計初期在Matlab下對濾波器原理進行證明包括(零極點圖、時域和頻域分析圖等),分析FIR數字濾波器的多種理論設計思想和窗函數選擇方法,在設計后期對FIR數字濾波器的小數乘法問題進行單獨論證。然后對分析出來的問題進行論證和解決,最后在Quartus Ⅱ中進行仿真驗證。
1.4 相關概念說明
數字濾波器(Digital filter)是由數字乘法器、加法器和延時單元組成的一種裝置。其功能是對輸入離散信號的數字代碼進行運算處理,以達到改變信號頻譜的目的。可認為是一個離散時間系統按預定的算法,將輸入離散時間信號轉換為所要求的輸出離散時間信號的特定功能裝置FIR(Finite Impulse Response )由線性系統理論可知,在某種適度條件下,輸入到線性系統的一個沖擊完全可以表征系統。當我們處理有限的離散數據時,線形系統的響應(包括對沖擊的響應)也是有限的。若線性系統僅是一個空間濾波器,則通過簡單地觀察它對沖擊的響應,我們就可以完全確定該濾波器。通過這種方式確定的濾波器稱為有限沖擊響應(FIR)濾波器。
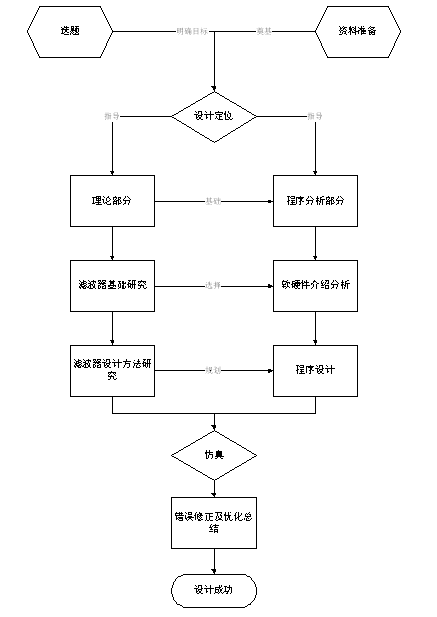
圖1-1總體設計流程圖
2 FIR數字濾波器的設計方法
2.1 理論部分
2.1.1? 引言
數字濾波器的功能一般是用來變換時域或者頻域中某些要求信號的屬性,濾除信號中某一部分頻率分量。經過數字濾波器的信號是讓其頻譜與數字濾波器的頻率響應相乘從而得出新的結果。經過一個線性卷積過程,從時域上輸入信號與濾波器的單位沖擊響應作一個卷積和。下面是卷積定義式:
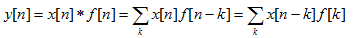 (1)
(1)
LTI數字濾波器在一般情況下分為有限脈沖響應(Finite impulse response)和無限脈沖響應(Infinite impulse response),FIR數字濾波器的設計方法和IIR濾波器的設計方法有很大的差別。因為其設計方向是選擇有限長度的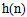 ,使頻率響應函數
,使頻率響應函數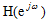 滿足指標。數字濾波器正在用直接的電子計算機規范和算法進行分析的方式來逐漸代替傳統的模擬濾波器的RLC元器件和放大電路。
滿足指標。數字濾波器正在用直接的電子計算機規范和算法進行分析的方式來逐漸代替傳統的模擬濾波器的RLC元器件和放大電路。
2.1.2? FIR數字濾波器的基礎
首先介紹FIR數字濾波器基本原理,在如下表格中對FIR和IIR數字濾波器進行了全面的比較:
表2-1兩種濾波器特點比較分析

通常情況下一般數字濾波器的N階FIR數字濾波器基于輸入信號x(n)的表達式為:
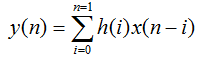
(2)
這個公式給我們了一個非常明了的直接型網絡結構,該結構表現出N個乘法器,每次采樣y(n)的內容是n次乘法和n-1次加法,然后做乘累加之和。如圖2-1所示:
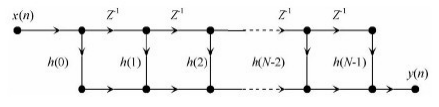
圖2-1 FIR濾波器直接型網絡結構
從DSP的介紹中,第一類線性相位對h(n)的約束條件:
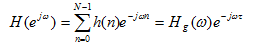 ?(3)
?(3)
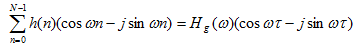 (4)
(4)
由公式(3),(4)我們可以推出:
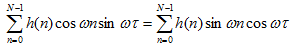 ?(5)
?(5)
移相并利用三角公式化簡得到:
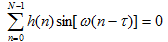 ?(6)
?(6)
從數字信號處理學科中知道函數關于求和區間的中心(N-1)/2奇對稱,于是我們要求和h(n)滿足如下條件:
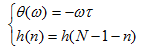
其中對應的有:
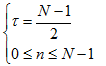 (7)
(7)
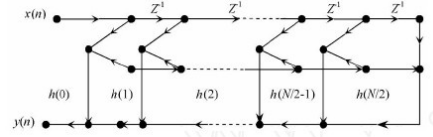
圖2-2 線性相位FIR濾波器結構
若h(n)呈現對稱特性,即此具有線性相位的濾波器是FIR數字濾波器。濾波器的基礎網絡結構可以相互進行轉換。
在前面本篇已經討論過, FPGA的實現中將對各種方法進行比較,找出最優設計方式。從而達到減少資源占有和提高系統作業速度的目的,更好的體現實時性的數字濾波器優勢。
2.1.3? 數字濾波器的設計原理
在數字信號處理技術的研究中,一般是使用的三種設計方法:窗函數法,FDATool直接設計法,程序編譯法。本文首先使用窗函數和Matlab軟件共同進行設計。
隨著技術的不斷發展,Matlab軟件能給設計者帶來的數字信號處理工作已經非常的完善和多樣了,設計者可以利用Matlab軟件進行數字濾波器的設計和仿真,而且還可以用這款軟件進行設計的優化。數字濾波器的一般設計步驟如下:
1.指標的確定
做任何工程或者設計,設計者都必須要有一個期望的指標用來限制設計范圍。在很多的實際應用中,設計者常常都是使用數字濾波器做選頻的工作。因此,指標的形式一半在頻域中給出相位響應和幅度。相位響應的指標形式,一半是指系統在通頻帶中藥有線性相位。幅度指標:絕對指標,它給出對幅度響應函數的要求,一般用于FIR濾波器的設計。相對指標,以分貝值的形式給出具體限制。
2.逼近目標
設計者做高頻的時候大概都有一個模式,就是首先得到技術指標,然后利用我們的技術和工具讓我們的產品去逼近這個指標。同理我們首先建立以個目標的數字濾波器模型。一般情況下都是采用理想的數字濾波器模型,然后去逼近我們想要的目標數字濾波器參數。
3.計算機仿真和性能優化分析
在工作中我們發現通過(1)、(2)之后本文會得到以差分、系統函數或者沖擊響應這三種方式描述的濾波器。這個時候設計者可以利用計算進行仿真,在系統中分析技術指標和濾波結果是否是希望得到的結果。
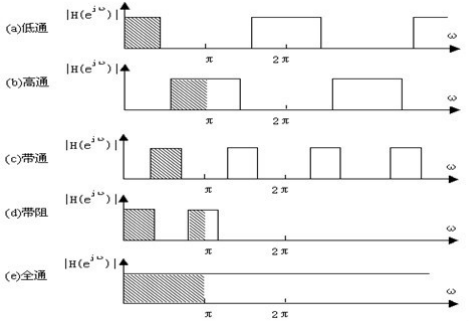
圖2-3各種理想數字濾波器的幅度頻率響應
2.1.4? FIR數字濾波器的理論計算方式與參數轉換思想
在理論上掌握了FIR數字濾波器的基本原理之后,本文需要對設計思想進行一個多方位的論證和嘗試。首先設計者設計濾波器要有一個硬性的指標,這個指標可以是直接給出最基本的數據,也有多重表現形式。于是我例舉兩種特殊的指標形式然后加以解決設計。然后我們分別用2種方式來設計不同指標的濾波器。接下來我首先用程序的方式來實現濾波器:
1.逼近法轉換與思想
使用remez函數設計FIR低通濾波器
設計濾波器,使逼近低通濾波特性|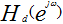 |。
|。
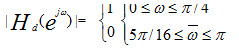
要求通帶波紋?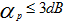 ,阻帶衰減
,阻帶衰減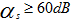 ,并用最小階數實現。
,并用最小階數實現。
繪出設計的FIR數字濾波幅頻特性曲線,檢驗設計指標。
這個指標我們可以以如下計算方法來得出詳細指標:
從給出的低通濾波特性|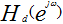 |。我們可以看出設計參數f=[1/4,5/16],m=[1,0];
|。我們可以看出設計參數f=[1/4,5/16],m=[1,0];
dev的計算根據公式: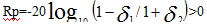
于是有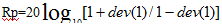 ,
,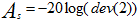
所以dev(1),dev(2)可以被表示出來。
2.逼近法程序描述與思想
有了這幾個參數我們現在就可以根據已經設定好的格式來調用函數remezord和remez函數了,于是可得如下程序。
?
?
clear;close all
fc=1/4;fs=5/16; %輸入給定指標
Rp=3;As=60;Fs=2;
f=[fc,fs];m=[1,0]; %計算remezord函數所需參數f,m,dev
dev=[(10^(Rp/20)-1)/(10^(Rp/20)+1),10^(-As/20)];
[N,fo,mo,W]=remezord(f,m,dev,Fs); %確定remez函數所需參數
hn=remez(N,fo,mo,W); %調用remez函數進行設計
hw=fft(hn,512); %求設計出的濾波器頻率特性
w=[0:511] *2/512;
plot(w,20*log10(abs(hw)));grid; %畫對數幅頻特性圖
axis([0,max(w)/2,-90,5]);
xlabel('w/pi');ylabel('Magnitude(dB)')
line([0,0.4],[-3,-3]); %畫線檢驗設計結果
line([1/4,1/4],[-90,5]);line([5/16,5/16],[-90,5]);
?
?
3.仿真圖像與結果
用以上的程序我們可以得到在Matlab中的許多參數和圖像,從而進一步分析我們的設計。首先引入程序輸出的幅頻特性圖:(如圖2-4)
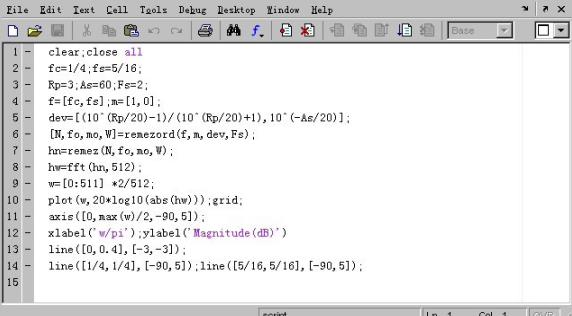
圖2-4在Matlab中的程序
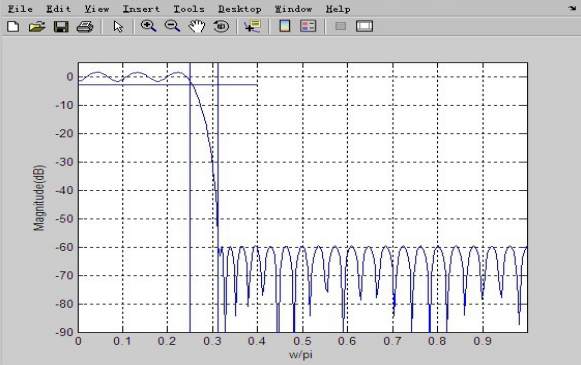
圖2-5程序輸出的幅頻特性
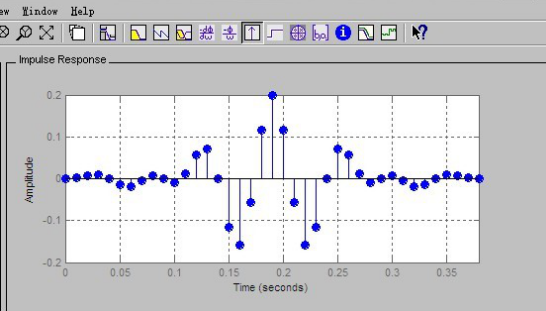
圖2-6 Impulse Response
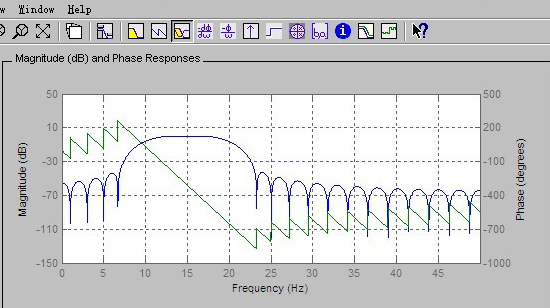
圖2-7 Magnitude and Phase Responses
圖2-8 Phase Delay
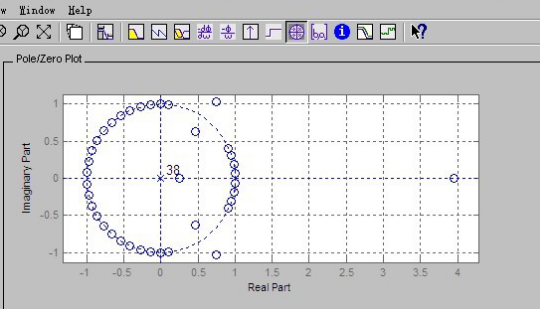
圖2-9 Pole,Zero plot
結論:從上面程序運行情況分析,觀察程序輸出的幅頻特性圖中橫線為-3dB,兩條豎線分別位于頻率π/4和5π/16。顯然,通帶指標有富裕,零極點圖反應出大部分零極點在圓內,過渡帶寬度和阻帶最小衰減剛好滿足指標要求。
4.窗函數選擇法與規劃思想
表2-2窗函數選擇指標
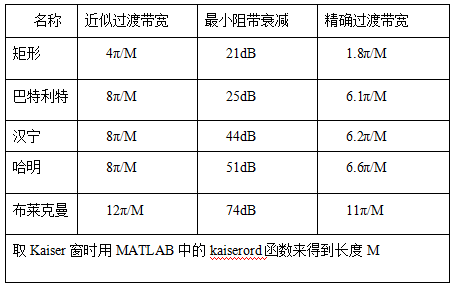
在設計指標中沒有直接給出窗函數的,可以利用下面這個表格進行篩選,具體方法如下:
這個表格給出了近似過渡帶寬、精確過渡帶寬和最小阻帶衰減,我們可以根據自己濾波器的參數來選擇我們的窗函數,因為選擇不同的窗函數設計出來的濾波器生成的過渡帶寬度和阻帶最小衰減是不同的。在這里我以一個例子來說明函數的選擇方式:
用窗函數法設計FIR帶通濾波器。指標如下:
高端通帶截止頻率: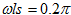
高端阻帶截止頻率: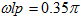
低端阻帶截止頻率: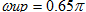
低端通帶截止頻率: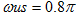
通帶最大衰減??Rp=1dB
阻帶最小衰減??Rs=60dB
在這樣一個例子中,可以看到它明確的給出了Rs=60dB來設置窗函數類型和階次。表格中給出的blackman窗其濾波器阻帶最小衰減是74dB,再利用給出的其他參數計算濾波器階數。表中顯示窗口長度M由過渡帶寬度B=0.8π-0.65π=0.15π決定,而Blackman窗設計的濾波器過渡帶寬度為12π/M,則M=12/0.15=80。又因M=N+1,所以濾波器階數N=79。?
在了解了怎么選擇窗函數和計算濾波器階數之后,本論文將針對實際FIR數字濾波器進行研究。已經給出了設計參數,下面開始利用MATLAB程序來設計這個濾波器。
5.窗函數法程序描述與思想
程序和對應的解釋:
?
?
%用窗函數法設計FIR帶通濾波器 clear;close?all; wls=0.2*pi;wlp=0.35*pi;whp=0.65*pi; B=wlp-wls;??????????????%這里是在計算過渡帶寬 N=ceil(12/0.15);????????%計算窗口長度 wc=[wlp/pi-6/N,whp/pi+6/N];??%設置理想帶通截止頻率 hn=fir1(N-1,wc,Blackman(N)); %設計濾波器參數
?
?
6.理論計算方法總結
仿真完成之后,掌握如何去利用已有的指標去設計一個濾波器,總的來說就是四項:
通過傅里葉逆變換獲得理想濾波器的單位脈沖響應hd(n)。
分析給定參數,計算出濾波器的階數,頻率等等相關指標。
把已經有的參數用程序函數表達出來,利用已經有的各種內置函數架設起濾波器。
參看Matlab的輸出圖形和參數是否滿足要求。
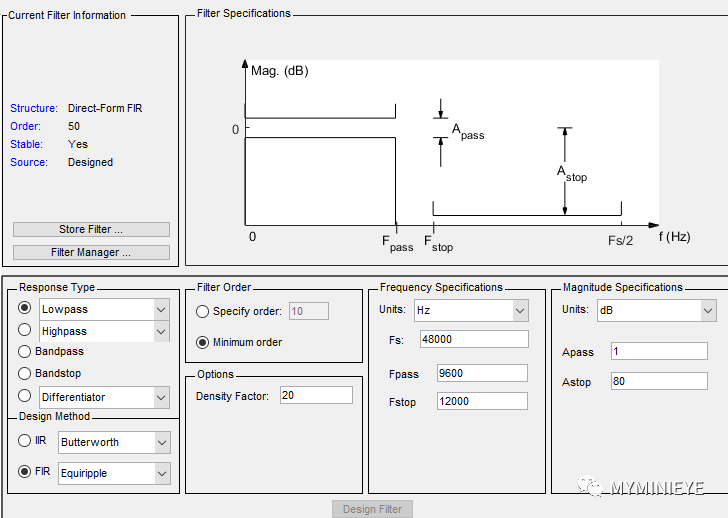
2.1.5? Matlab直接FDAtool設計方式解析
FDATool(Filter Design & Analysis Tool)是MATLAB信號處理工具箱里專用的濾波器設計分析工具,MATLAB6.0以上的版本還專門增加了濾波器設計工具箱(Filter Design Toolbox)。FDATool可以設計幾乎所有的基本的常規濾波器,包括FIR和IIR的各種設計方法。它操作簡單,方便靈活。
FDATool界面總共分兩大部分,一部分是Design Filter,在界面的下半部,用來設置濾波器的設計參數,另一部分則是特性區,在界面的上半部分,用來顯示濾波器的各種特性。Design Filter部分主要分為:
Filter Type(濾波器類型)選項,包括Lowpass(低通)、Highpass(高通)、Bandpass(帶通)、Bandstop(帶阻)和特殊的FIR濾波器。
Design Method(設計方法)選項,包括IIR濾波器的Butterworth(巴特沃思)法、Chebyshev Type I(切比雪夫I型)法、 Chebyshev Type II(切比雪夫II型) 法、Elliptic(橢圓濾波器)法和FIR濾波器的Equiripple法、Least-Squares(最小乘方)法、Window(窗函數)法。
Filter Order(濾波器階數)選項,定義濾波器的階數,包括Specify Order(指定階數)和Minimum Order(最小階數)。在Specify Order中填入所要設計的濾波器的階數(N階濾波器,Specify Order=N-1),如果選擇Minimum Order則MATLAB根據所選擇的濾波器類型自動使用最小階數。
Frenquency Specifications選項,可以詳細定義頻帶的各參數,包括采樣頻率Fs和頻帶的截止頻率。它的具體選項由Filter Type選項和Design Method選項決定,例如Bandpass(帶通)濾波器需要定義Fstop1(下阻帶截止頻率)、Fpass1(通帶下限截止頻率)、Fpass2(通帶上限截止頻率)、Fstop2(上阻帶截止頻率),而Lowpass(低通)濾波器只需要定義Fstop1、Fpass1。采用窗函數設計濾波器時,由于過渡帶是由窗函數的類型和階數所決定的,所以只需要定義通帶截止頻率,而不必定義阻帶參數。
Magnitude Specifications選項,可以定義幅值衰減的情況。例如設計帶通濾波器時,可以定義Wstop1(頻率Fstop1處的幅值衰減)、Wpass(通帶范圍內的幅值衰減)、Wstop2(頻率Fstop2處的幅值衰減)。當采用窗函數設計時,通帶截止頻率處的幅值衰減固定為6db,所以不必定義。
參數要求:采樣頻率fs=100Hz,通帶下限截止頻率fc1=10 Hz,通帶上限截止頻率fc2=20 Hz,過渡帶寬6 Hz,通阻帶波動0.01,采用凱塞窗設計。
針對一個含有5Hz、15Hz和30Hz的混和正弦波信號已知濾波器的階數n=38,beta=3.4。本例中,首先在Filter Type中選擇Bandpass;在Design Method選項中選擇FIR Window,接著在Window選項中選取Kaiser,Beta值為3.4;指定Filter Order項中的Specify order為38;采樣頻率Fs=100Hz,截止頻率Fc1=10Hz,Fc2=20Hz。設置完以后點擊窗口下方的Design Filter,在窗口上方就會看到所設計濾波器的幅頻響應,通過菜單選項Analysis還可以看到濾波器的相頻響應、組延遲、脈沖響應、階躍響應、零極點配置等。設計完成后將結果保存為kaiser15.fda文件。我們可以根據FDAtool工具得到我們的濾波器相關增益。
系數轉換成二進制碼:
若采用乘法器,用1位整數位,1位符號位,共22位定點二進制數進行運算,負數用補碼表示,由此將減法運算變成累加求和運算。各系數可用matlab編程轉成二進制補碼:?
?
?
/* General type conversion for MATLAB generated C-code */
#include "tmwtypes.h"
/*
* Expected path to tmwtypes.h
* D:MATLAB7externinclude mwtypes.h
*/
const int BL = 39;
const real64_T B[39] = {
-0.0008969942906957,0.001248746631882,0.007070735236406,0.009180571739749,-8.354434235897e-018,-0.01457672567709,-0.01798701306701,-0.005189936475222,0.006300913248271,-5.136773213647e-018,-0.009200436084654,0.01113207796169,0.05739543087552,0.07065284310647,-2.116878167777e-017,-0.1149210109554,-0.1575671556317,-0.05691148173912,0.1151784185022,0.2,0.1151784185022,-0.05691148173912,-0.1575671556317,-0.1149210109554,-2.116878167777e-017,0.07065284310647,0.05739543087552,0.01113207796169,-0.009200436084654,-5.136773213647e-018,0.006300913248271,-0.005189936475222,-0.01798701306701,-0.01457672567709,-8.354434235897e-018,0.009180571739749,0.007070735236406,0.001248746631882,-0.0008969942906957
};
?
?
這是一個非常典型的例子,可以清晰的看到利用Matlab提供的FDAtool設計濾波器的方便與快捷。比較以上幾種類型的濾波器參數,在給定的參數要求下,采用橢圓濾波器可以獲得最佳的幅頻響應特性,具有階數低,過渡帶窄等優點。雖然橢圓濾波器在通帶也會產生波動,但考慮到波動處在可接受的范圍內,仍然符合設計要求。
但由直接型傳輸函數表達式來實現并不實用。因此如前所說,將其分解為多個二階傳輸函數的級聯形式。借助Matlab 信號處理工具箱中函tf2sos(Transfer function to second- order- section)將傳遞函數轉換為二階級聯形式。
對于是數字信號,需要對先前分析計算中分解獲得的二階子系統的濾波器系數進行量化,即用一個固定的字長加以表示。量化過程中由于存在不同程度的量化誤差,由此會導致濾波器的頻率響應出現偏差,嚴重時會使濾波器的極點移到單位圓之外,使系統不穩定。為了獲得最優的濾波器系數,量化的精度也相當重要。
2.1.6 FDAtool設計模板及設計結果圖
這里把上面的濾波器設計參數的總體圖給出,如圖2-10
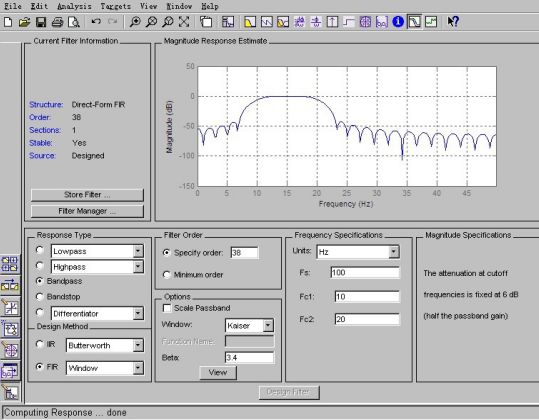
圖2-10 FIR帶通濾波器總體設計參數
2.2程序分析部分
根據上述FIR低通數字濾波器的原理與濾波特性,我們在上面的軟件實踐中已經掌握了設計數字濾波器的方法并且成功的使用Matlab/Simulink進行了設計和仿真。通過以上的過程我們可以導出一定性能的FIR濾波器頻率響應與抽頭系數,然后用Verilog HDL語言設計和QUARTUSⅡ仿真FIR低通數字濾波器,實現用軟件描述硬件的動作及功能,應用軟件來實現數字濾波器的功能和時序仿真。
2.2.1FPGA 可編程邏輯元件介紹
EDA是Electronic Design Automation的縮寫,意為電子設計自動化,即利用計算機自動完成電子系統的設計。EDA技術是以計算機和微電子技術為先導,匯集了計算機圖形學、拓撲、邏輯學、微電子工藝與結構學和計算數學等多種計算機應用學科最新成果的先進技術。
它與電子技術、微電子技術的發展密切相關,吸收了計算機領域的大多數最新研究成果,以高性能的計算機作為工作工具,在EDA軟件平臺土,根據硬件描述語言HDL完成的設計文件,自動地完成邏輯編譯、化簡、分割、綜合及優化、布線、仿真,直至對于特定目標芯片的適配編譯、邏輯映射和編程下載等工作。
可編程邏輯器PLD(Programmable Logic Devices)是ASIC(Application?Specific Integrated Circuits的一個重要分支。ASIC按制造方法又可分為全定制(Full Custom)產品、半定制(semi-custom)產品和可編程邏輯器件(PLD)。前兩種ASIC的設計和制造都離不開器件生產廠家,用戶主動性較差。隨著微電子技術的發展,設計師們更愿意自己設計專用集成電路芯片,并盡可能縮短設計周期,最好是在實驗室里就能設計出合適的ASIC芯片,并且立即投入實際應用之中,在使用中也能比較方便的對設計進行修改。可編程邏輯器件就是為滿足用戶的這一需求應運而生的。
使用FPGA器件設計數字電路,不僅可以簡化設計過程,而且可以降低整個系統的體積和成本,增加系統的可靠性。它們無需花費傳統意義下制造集成電路所需大量時間和精力,避免了投資風險,成為電子器件行業中發展最快的一族。使用FPGA器件設計數字系統電路的主要優點如下:
1.設計靈活
使用FPGA器件,可不受標準系列器件在邏輯功能上的限制。而且修改邏輯可在系統設計和使用過程的任一階段中進行,并且只須通過對所用的FPGA器件進行重新編程即可完成,給系統設計提供了很大的靈活性。
2.增大功能密集度
功能密集度是指在給定的空間能集成的邏輯功能數量。可編程邏輯芯片內的組件門數高,一片FPGA可代替幾片、幾十片乃至幾百片中小規模的數字集成電路芯片。用FPGA器件實現數字系統時用的芯片數量少,從而減少芯片的使用數目,減少印刷線路板面積和印刷線路板數目,最終導致系統規模的全面縮減。
3.提高可靠性
減少芯片和印刷板數目,不僅能縮小系統規模,而且它還極大的提高了系統的可靠性。具有較高集成度的系統比用許多低集成度的標準組件設計的相同系統具有高得多的可靠性。使用FPGA器件減少了實現系統所需要的芯片數目,在印刷線路板上的引線以及焊點數量也隨之減少,所以系統的可靠性得以提高。
4.縮短設計周期
基于FPGA器件的可編程性和靈活性,用它來設計一個系統所需時間比傳統方法大為縮短。FPGA器件集成度高,使用時印刷線路板電路布局布線簡單。同時,在樣機設計成功后,由于開發工具先進,自動化程度高,對其進行邏輯修改也十分簡便迅速。因此,使用FPGA器件可大大縮短系統的設計周期,加快產品投放市場的速度,提高產品的競爭能力。
5.工作速度快
FPGA/CPLD器件的工作速度快,一般可以達到幾百兆赫茲,遠遠大于DPS器件。同時,使用FPGA器件后實現系統所需要的電路級數又少,因而整個系統的工作速度會得到提高。
6.增加系統的保密性能
很多FPGA器件都具有加密功能,在系統中廣泛的使用FPGA器件可以有效防止產品被他人非法仿制。
7.降低成本
使用FPGA器件實現數字系統設計時,如果僅從器件本身的價格考慮,有時還看不出來它的優勢,但是影響系統成本的因素是多方面的,綜合考慮,使用FPGA的成本優越性是很明顯的。首先,使用FPGA器件修改設計方便,設計周期縮短,使系統的研制開發費用降低;其次,FPGA器件可使印刷線路板面積和需要的插件減少,從而使系統的制造費用降低;再次,使用FPGA器件能使系統的可靠性提高,維修工作量減少,進而使系統的維修服務費用降低。總之,使用FPGA器件進行系統設計能節約成本。
2.2.2 QuartusⅡ及Verilog HDL介紹
Quartus II 是 Intel 公司的綜合性開發軟件,支持原理圖、VHDL、VerilogHDL以及AHDL(Altera Hardware Description Language)等多種設計輸入形式,內嵌自有的綜合器以及仿真器,可以完成從設計輸入到硬件配置的完整PLD設計流程。
Quartus II可以在XP、Linux以及Unix上使用,除了可以使用Tcl腳本完成設計流程外,提供了完善的用戶圖形界面設計方式。具有運行速度快,界面統一,功能集中,易學易用等特點。
Quartus II支持Altera的IP核,包含了LPM/MegaFunction宏功能模塊庫,使用戶可以充分利用成熟的模塊,簡化了設計的復雜性、加快了設計速度。對第三方EDA工具的良好支持也使用戶可以在設計流程的各個階段使用熟悉的第三方EDA工具。
此外,Quartus II 通過和 DSP Builder工具 與 Matlab/Simulink相結合,可以方便地實現各種DSP應用系統;支持Altera的片上可編程系統(SOPC)開發,集系統級設計、嵌入式軟件開發、可編程邏輯設計于一體,是一種綜合性的開發平臺。?
Maxplus II 作為Altera的上一代PLD設計軟件,由于其出色的易用性而得到了廣泛的應用。目前 Altera 已經停止了對Maxplus II 的更新支持,Quartus II 與之相比不僅僅是支持器件類型的豐富和圖形界面的改變。Altera在Quartus II 中包含了許多諸如SignalTap II、Chip Editor和 RTL Viewer 的設計輔助工具,集成了SOPC和HardCopy設計流程,并且繼承了Maxplus II 友好的圖形界面及簡便的使用方法。
Altera Quartus II 作為一種可編程邏輯的設計環境, 由于其強大的設計能力和直觀易用的接口,越來越受到數字系統設計者的歡迎。
Verilog HDL是目前應用最為廣泛的硬件描述語言。Verilog HDL可以用來進行各種層次的邏輯設計,也可以進行數字系統的邏輯綜合,仿真驗證和時序分析等。該語言適合算法級,寄存器級,邏輯級,門級和版圖級等各個層次的設計和描述。Verilog HDL進行設計最大的優點是其工藝無關性。這使得我們在功能設計,邏輯驗證階段可以不必過多考慮門級及工藝實現的具體細節,只需根據系統設計的要求施加不同的約束條件,即可設計出實際電路。VerilogHDL是一種硬件描述語言(hardware description language),為了制作數字電路而用來描述ASIC和FPGA的設計之用。VerilogHDL 的設計者想要以 C 編程語言為基礎設計一種語言,可以使工程師比較容易學習。
2.2.3實際濾波器程序設計(11階FIR數字濾波器)
FPGA實現FIR濾波器,首先進行指標選定和Matlab軟件參數仿真,然后執行基于Verilog方法的硬件實現中用移位方法代替了乘法運算。
表2-3設計指標要求
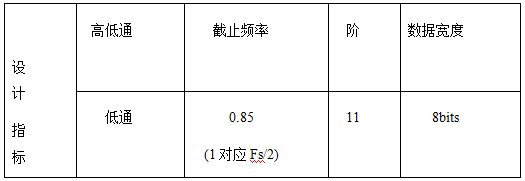
根據以上指標,利用MATLAB中的FIR濾波器系數設計命令fir1(10,0.85)所設計濾波器的系數。
表2-4 Matlab中導出的濾波器系數

MATLAB軟件仿真的濾波器的抽頭系數及其幅度頻響特性如下圖2-11所示。
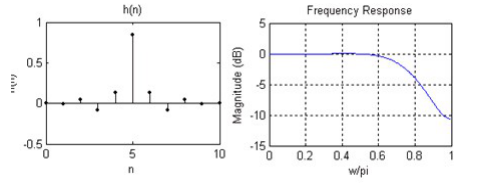
圖2-11 11階FIR濾波器的抽頭系數和幅頻特性曲線
可見抽頭系數是奇對稱的,即:
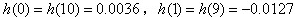 ,
,
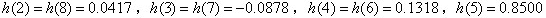 。
。
FIR濾波器采用對稱結構,每個抽頭的輸出分別乘以相應加權的二進制值,再將結果相加。同時,利用濾波器系數的及對稱的特性,對輸入信號?進行如下等效:?
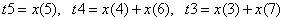 ,?
,?
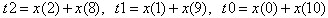 。
。
2.2.4.VerilogHDL的實現
這個方法的實現中,使用了移位代替乘法運算來實現濾波器乘加的方法。由于濾波器系數都是小數,所以我們先左移7位(即放大128倍),再用相應的移位來近似這些系數,最后經過乘加運算得到結果,對這個結果再右移7位(即縮小128倍)即可得出正確的結果。各個系數的移位情況如下:其中2表示左移1位,1表示不移位,0.5表示右移1位,其他依次類推:
128×h(0)=128×0.036=0.4608=0.5-0.03125
128×h(1)=128×0.0127=1.6256=1+0.5+0.125
128×h(2)=128×0.0417=5.3376=4+1+0.25+0.625+0.03125
128×h(3)=128×0.0878=11.2384=8+4-1+0.25
128×h(4)=128×0.1318=16.8704=16+1-0.125
128×h(5)=128×0.8500=108.800=128-16-4+0.25+0.0625
這樣,我們就可以把這個11階FIR數字濾波器的輸出用一下的算式得到
表2-5 Verilog方法設計FIR的實驗數據
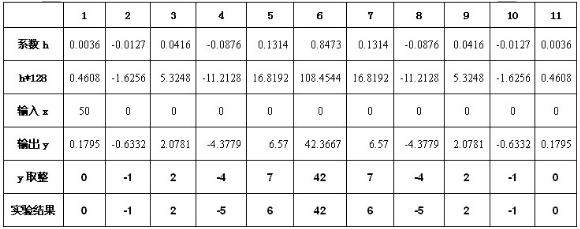

圖 2-12系數放大后求SUM
計算得到結果后再將sum右移7位,即可得到正確結果。程序的功能仿真結果如下圖2-12所示。

圖2-13功能仿真
由上圖2-12可以看出,tap0到tap10是輸入x的依次延時1個時鐘周期,結果sum輸出相對于輸入x延遲了2個時鐘周期,y輸出相對于sum輸出延遲了1個時鐘周期,這和程序設計相符合。同時,對比程序運行結果和MATLAB的計算結果(如章節開頭表格所示),可知,二者結果是一致的,其中個別數據的小誤差是由于移位取代小數乘法運算帶來的誤差。因此,程序設計是正確的。
于是,根據以上所有思想我們可以得出以下11階FIR數字濾波器的Verilog程序如下:
?
?
module firv2(clk, x, y);
input clk;
?input?[7:0]?x;
?output?[25:0]?y;
reg [26:0] y;
reg[7:0] x0,x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15,x16;
wire[21:0] acc1,acc2,acc3,acc4,acc5,acc6,acc7,acc8,acc9,acc10,acc11,acc12,acc13,acc14,acc15,acc16,acc17;
reg [8:0]sxin[0:32];
reg [5:0]i,k;
reg [8:0]xx[16:0];
parameter c0=-21,
c1=-8,
c2= 22,
c3=34,
c4=6,
c5=-34,
c6=-31,
c7=32,
c8=87,
c9=32,
c10=-154,
c11=-321,
c12=-217,
c13=321,
c14=1185,
c15=1996,
c16=2328;
always @ (posedge clk)
begin
xx[16]<=sxin[16] ;
for(i=0;i<16;i=i+1)
xx[i]<=sxin[i]+sxin[32-i] ;
for(k=32;k>0;k=k-1)
?????sxin[k]<=sxin[k-1];?
?????sxin[0]<={x[7],x};
end
mult13_8 uut0(clk,c0,xx[0],acc1);
mult13_8 uut1(clk,c1,xx[1],acc2);
mult13_8 uut2(clk,c2,xx[2],acc3);
mult13_8 uut3(clk,c3,xx[3],acc4);
mult13_8 uut4(clk,c4,xx[4],acc5);
mult13_8 uut5(clk,c5,xx[5],acc6);
mult13_8 uut6(clk,c6,xx[6],acc7);
mult13_8 uut7(clk,c7,xx[7],acc8);
mult13_8 uut8(clk,c8,xx[8],acc9);
mult13_8 uut9(clk,c9,xx[9],acc10);
mult13_8 uut10(clk,c10,xx[10],acc11);
mult13_8 uut11(clk,c11,xx[11],acc12);
mult13_8 uut12(clk,c12,xx[12],acc13);
mult13_8 uut13(clk,c13,xx[13],acc14);
mult13_8 uut14(clk,c14,xx[14],acc15);
mult13_8 uut15(clk,c15,xx[15],acc16);
mult13_8 uut16(clk,c16,xx[16],acc17);
always @(posedge clk)
begin
y<={acc16[1],acc16[1],acc16[1],acc16[1],acc16[1],acc16}+{acc17[1],acc17[1],acc17[1],acc17[1],acc17[1],acc17}
+{acc15[1],acc15[1],acc15[1],acc15[1],acc15[1],acc15}+{acc14[1],acc14[1],acc14[1],acc14[1],acc14[1],acc14}
+{acc13[1],acc13[1],acc13[1],acc13[1],acc13[1],acc13}+{acc12[1],acc12[1],acc12[1],acc12[1],acc12[1],acc12}
+{acc11[1],acc11[1],acc11[1],acc11[1],acc11[1],acc11}+{acc10[1],acc10[1],acc10[1],acc10[1],acc10[1],acc10}
+{acc9[1],acc9[1],acc9[1],acc9[1],acc9[1],acc9}+{acc8[1],acc8[1],acc8[1],acc8[1],acc8[1],acc8}
+{acc7[1],acc7[1],acc7[1],acc7[1],acc7[1],acc7}+{acc6[1],acc6[1],acc6[1],acc6[1],acc6[1],acc6}
+{acc5[1],acc5[1],acc5[1],acc5[1],acc5[1],acc5}+{acc4[1],acc4[1],acc4[1],acc4[1],acc4[1],acc4}
+{acc3[1],acc3[1],acc3[1],acc3[1],acc3[1],acc3}+{acc2[1],acc2[1],acc2[1],acc2[1],acc2[1],acc2}
+{acc1[1],acc1[1],acc1[1],acc1[1],acc1[1],acc1};
end
endmodule
?
?
1.分析程序設計
使用MAC單元完成乘加運算(包括單MAC和多MAC的情況)這個方法可以利用FPGA中已有的MAC單元(像Xilinx Spartan 3E-100中有四個乘加單元),只要設計好數據運算流程,就能方便高效地實現FIR運算。使用MAC單元還有一個優點是系數可以存成系數表,可以方便地修改,這是移位方法代替乘法運算所不及的。
使用移位代替乘法運算這個方法的優點是速度快,例如11階的濾波器,完成一次運算需要11次乘法,如果使用單MAC的話,需要11個時鐘周期來完成,而使用移位方法可以在一個時鐘周期完成11個乘法運算;缺點是需要另外去完成濾波系數到移位位數的換算,如果修改濾波系數的話,程序修改將會比較麻煩,同時硬件資源也要使用多一些。
t*0.125={t[7],t[7],t[7],t[7:3]} t*0.125?=?t/8?=?t>>3; t為有符號數,所以是帶符號右移,于是t>>3?={t[7],t[7],t[7],t[7:3]} 之所以這么些就是為了節省資源,提高頻率
以?-4*0.5?為例? -4的原碼:1000?0100B??補碼:1111?1100B -4>>1=0111?1110 而符號位不能變?應用原來的位代替?1111?1110B?的原碼?1000?0010B?=-2
2.?對程序設計中的問題分析與總結
在最開始的設計中,本文初始計劃使用乘法單元。但是在程序設計的過程中我們遇見了實數乘法的問題,程序的運行遇到了困難,在與指導老師的研究中我們發現問題出在實數乘法的問題上。在Verilog的運算中實數乘法需要特殊的小數乘法器來單元來實現。在原來的38階濾波器的設計中出現了這樣子的問題。我們使用過這樣的程序:
?
?
reg [63:0] filter_in_force [0:3344];
reg [63:0] filter_out_expected [0:3344];
// Function definitions
function real abs_real;
input real arg;
begin
abs_real = arg > 0 ? arg : -arg;
end
endfunction //function abs_real
// Component Instances
filter u_filter
(
.clk(clk),
.clk_enable(clk_enable),
.reset(reset),
.filter_in(filter_in),
.filter_out(filter_out)
);
initial
begin
// Constants
filter_in_force [0] <= $realtobits(1.0000000000000000E+000);
filter_in_force [1] <= $realtobits(0.0000000000000000E+000);
filter_in_force [2] <= $realtobits(0.0000000000000000E+000);
filter_in_force [3] <= $realtobits(0.0000000000000000E+000);
…
?
?
系統無法實現real值得計算,于是這里需要我們用小數乘法器進行特殊單元的方案解決。于是我們要進行小數乘法器的設計。
3.小數乘法器介紹及在設計中的作用
隨著FPGA 的發展以及相應EDA 軟件工具的成熟,FPGA 在高速數字信號處理領域得到了越來越廣泛的應用。而乘法,尤其是浮點乘法運算是數值計算和數據分析中最常用的運算之一。目前,多數FPGA 上可以實現整數和標準邏輯矢量的乘法,但不支持浮點乘法運算, 因此使得FPGA 在數值計算、數據分析和信號處理等方面受到了限制。本文采用適合于FPGA 實現的自定義26 位浮點數據格式,利用改進的基4Boot h 編碼運算方式,以及CSA和4 - 2 壓縮器綜合的Wallace 樹形結構,減少了部分積,使系統具有高速度,低功耗的特點,并且結構規則。在尾數的舍入中采用了基于預測和選擇的舍入方法,進一步提高了運算的速度,優化了乘法器的性能。
4.小數乘法器程序設計與仿真
?
?
modulefix_mult ( clk,rst_n,in_a,in_b,x1,x2,x3,x4,x5,x6,x7,y_out );
inputclk,rst_n;//時鐘和復位信號
input[31:0] in_a,in_b;//輸入的被乘數和乘數
output[31:0] y_out;//輸出的乘積
/*寄存器類型變量 為了能更清楚的了解全處理過程,
特地設計為輸出的,不然仿真可能會被綜合掉*/
output[15:0] x1,x2,x3,x4;
output[0:0] x5;
output[29:0] x6;
output[31:0] x7;
/////////////////////////////////////////////////////
reg[31:0] y_out;
reg[15:0] x1,x2,x3,x4;
reg[0:0] x5;
reg[29:0] x6;
reg[31:0] x7;
always@ (posedgeclk )
begin
if(!rst_n )//復位時,全部寄存器變量清零
begin
x1<=16'b0;
x2<=16'b0;
x3<=16'b0;
x4<=16'b0;
x5<=1'b0;
x6<=30'b0;
x7<=32'b0;
y_out<=32'b0;
end
else/
begin
x1<=in_a[31:16];//截取16位被乘數,
x2<=in_b[31:16];//截取16位乘數
x3<=(x1[15]==0)?x1:{x1[15],~x1[14:0]+1'b1}; //據最高位判斷是否為負數,
//若負數則把補碼轉成原碼
x4<=(x2[15]==0)?x2:{x2[15],~x2[14:0]+1'b1};
x5<=x3[15]^x4[15];//兩數符號位相異或,得到乘積的符號位
x6<=x3[14:0]*x4[14:0];//兩數的數據位相乘
x7<={x5,x6,1'b0}; //乘積由1位符號位和30位數據位及1位無關組成;
//因為是小數,往低位生長,所以無關位放置最低位
y_out<=(x7[31]==0)?x7:{x7[31],~x7[30:0]+1'b1};
end
end
endmodule
?
?
小數乘法器的仿真結果如下圖2-14所示:

圖2-14小數乘法器仿真結果
全過程可以看成:把32位的小數截取高16位左移16位,變為16位整數相乘得到32位整數乘積后,右移32位調整無關位的位置得到32位小數,這樣就可以完成早期程序中的小數乘法功能,然后來進行設計中的FPGA數字濾波器設計的優化。
在先前的設計中我們使用Matlab進行綜合仿真設計,并且借助FDAtool設計出濾波器。在Quartus II 的仿真中我們發現程序無法正常的完成運行,究其原因在于小數乘法器的問題。在原來的濾波器中需要對每一個參數進行單獨設置,這樣會使得程序占有巨量的篇幅大大的增加了工作量和容錯度。于是,我們需求另外一種方法來解決這個問題,后來我們研究了移位算法。利用移位來把小數運算轉換成整數運算,這樣我們的11階濾波器程序大大減少篇幅同時也增加了程序的可讀程度和穩定程度。
3?濾波器仿真濾波
3.1設置混合信號
在Matlab中進行我們設計過的FIR數字濾波器的仿真,首先我們啟動Matlab中的Simulink,啟動方式是直接在文本窗口中輸入命令Simulink,或者點擊Matlab中的快速啟動按鈕。
圖2-15 Simulink工具窗口圖
本論文模擬一個混合信號正弦波信號他包涵了10,30,60(Hz)的信號,在Matlab模擬出來是這樣一個信號:
?
?
Fs=200;
t=(1:200)/Fs;
x1=sin(2*pi*t*10);
x2=sin(2*pi*t*30);
x3=sin(2*pi*t*60);
X= x1+ x2+ x3;
plot(t,X);
title('混合正弦波信號X(t)-濾波前');
grid;
Module end
//整個模擬濾波信號結束
//使用軟件仿真出待濾波信號
?
?
混合信號設定之后利用Matlab工具進行模型仿真。
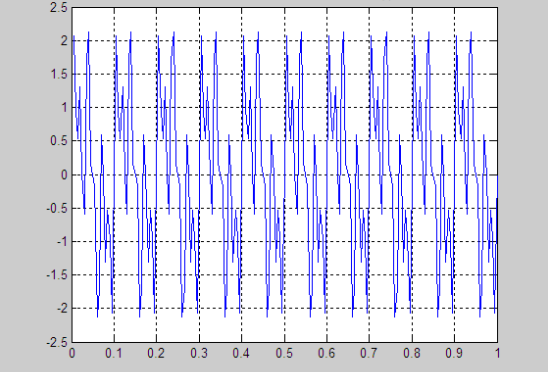
圖2-16 Matlab中模擬的混合信號
然后在程序中設置好仿真模型如下圖(2-17)
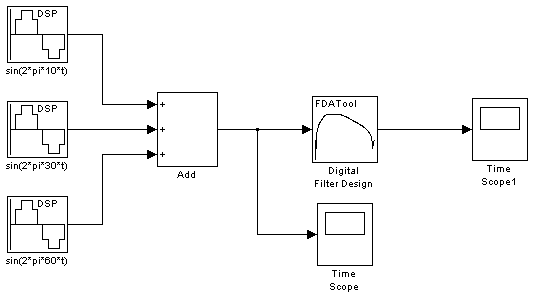
圖2-17 Simulink模型仿真
3.2設置仿真參數
設置好仿真參數,對各個信號進行單獨修改和設置如下圖(2-18):
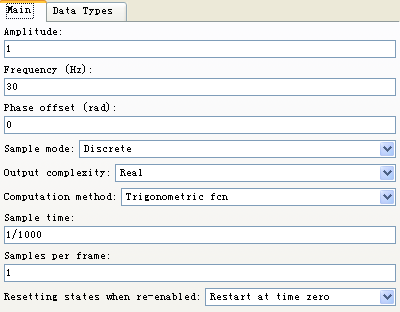
圖2-18 sin(2*pi*30*t)參數模塊
在主設置中,振幅(Amplitude)設置為1,?????????????????????????????????????
頻率(Frequency)設置為30Hz,????????????????????????????????????????????
輸出混合為實常量,樣本時間為1/1000,???????????????????????????????????????
采樣幀數設置為1幀,以下不同頻率信號同理設置:
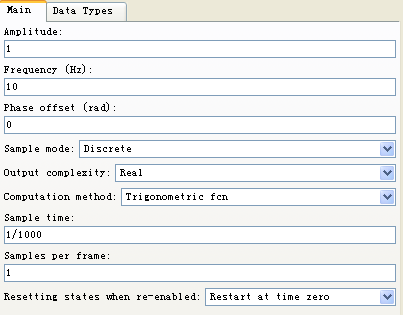
圖2-19 sin(2*pi*10*t)參數模塊
圖2-20 混合參數模塊
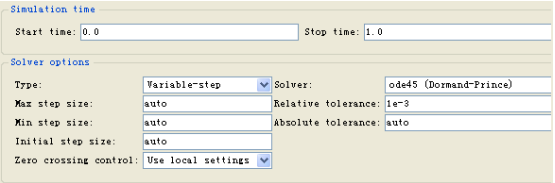
圖2-21 仿真設計模塊
最后來設置仿真參數:在Matlab模型窗口打開菜單[Simulation:Configuration Parameters];找到【SimulationConfiguration Parameters】對話框,設置仿真參數如下Configuration Parameters設置完成之后運行:可以直接點擊模塊窗口中的 ,開始進行仿真。輸出結果如圖2-22所示:
,開始進行仿真。輸出結果如圖2-22所示:
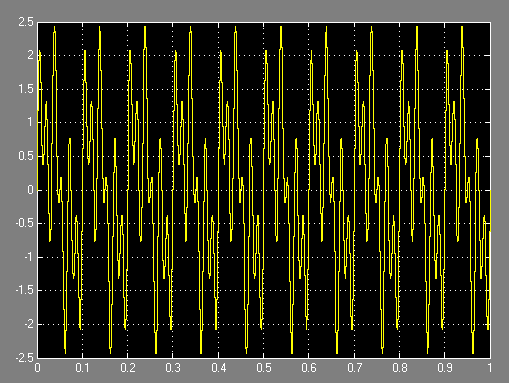
圖2-22 濾波前信號波形圖
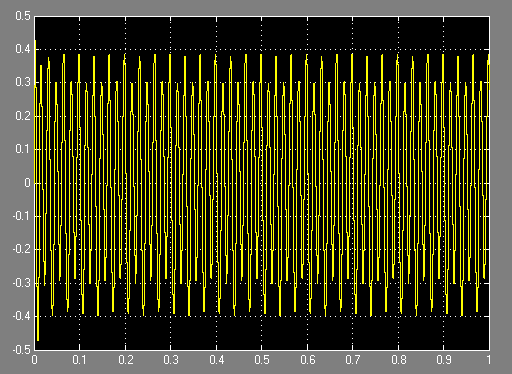
圖2-23濾波后信號波形圖
3.3 仿真總結
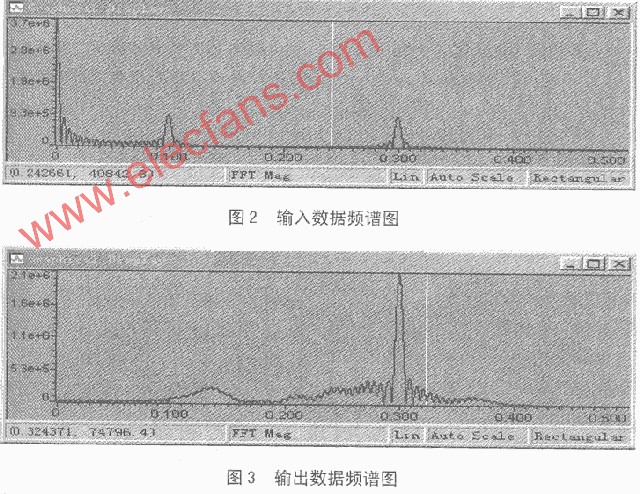
由上面的仿真結果輸出圖可以看出,所設計的數字帶通濾波器使混合輸入信號中頻率為30Hz的正弦波信號通過,明顯的出現了帶中信號。而將頻率為10Hz和60Hz的正弦波信號大大衰減,從而達到濾波效果。用Matlab Simulink仿真數字濾波器設計更加直觀,操作便捷,易于分析。
4 總結與展望
4.1 設計成果總結
在理論積累和重復實踐的基礎上,多種濾波器設計思路已經相當成熟,設計出來的濾波器通過仿真概率高,仿真結果符合設計要求。FIR數字濾波器的設計方式選擇更具有科學性和時效性,可以根據自己熟悉的軟件,需要的FIR數字濾波器的精度,FIR數字濾波器的類型和濾波器階數來靈活選擇設計思路和方法。
4.2 設計心得
本次畢業設計主要包含了信號與系統,數字信號處理和FPGA方面的相關知識。設計心得總結如下:
設計路徑優化?確定好所需要設計的FIR數字濾波器濾波器后,首先對其進行性能需求分析,明確FIR數字濾波器系統應該達到的各種性能指標,其次,擬定多種濾波器類型,對這些方案采用Matlab進行仿真,在這個過程中我們有許多的窗函數選擇和設計方法選擇,進行綜合分析和比較,選擇出最佳的濾波器類型作為本設計方案,然后依據其性能指標編寫Matlab程序,確定二階節系數,或者直接進行 Verilog HDL語言的編寫。
系統整體思維細節決定整體,整體展現細節。我們的設計必須有系統的設計思維,把每一個細節都融入到整個系統中考慮,去發現整個FIR數字濾波器系統的主觀性、完整性、穩定性和仿真功能的實現,才能讓各個細節完美縫合,才能快速的完成性能優越的硬件設計。
多做設計嘗試和總結,在FIR數字濾波器的設計中遇到過很多困難甚至是障礙。但是必須堅持自己的設計思路,去尋找其他的解決方法比如本論文中所提到的小數乘法器。這個本來是設計過程無法逾越的障礙,最后在不懈努力下,一樣做出的小數乘法器。并且我們要善于積累和總結讓障礙成為我們的另一種知識沉淀,這樣我們才能融會貫通,才能更善于發現問題和解決問題。無論在什么時候,科學的道路上永遠都是未知。我們應該一直堅持自己的原則,不拋棄,不放棄,這樣才能在這條充滿荊棘的路上走的更遠!
審核編輯:黃飛
 電子發燒友App
電子發燒友App










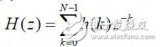




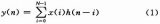
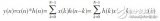
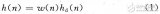











評論