1. 最佳優先搜索(Best-First Search)
最佳優先搜索(BFS),又稱A算法,是一種啟發式搜索算法(Heuristic Algorithm)。[不是廣度優先搜索算法( Breadth First Search , BFS )]
BFS算法在廣度優先搜索的基礎上,用啟發估價函數對將要被遍歷到的點進行估價,然后選擇代價小的進行遍歷,直到找到目標節點或者遍歷完所有點,算法結束。
要實現最佳優先搜索我們必須使用一個優先隊列(priority queue)來實現,通常采用一個open優先隊列和一個closed集,open優先隊列用來儲存還沒有遍歷將要遍歷的節點,而closed集用來儲存已經被遍歷過的節點。
1.1 最佳優先搜索的過程
最佳優先搜索的過程可以被描述為:
1、將根節點放入優先隊列open中。
2、從優先隊列中取出優先級最高的節點X。
3、根據節點X生成子節點Y:
X的子節點Y不在open隊列或者closed中,由估價函數計算出估價值,放入open隊列中。
X的子節點Y在open隊列中,且估價值優于open隊列中的子節點Y,將open隊列中的子節點Y的估價值替換成新的估價值并按優先值排序。
X的子節點Y在closed集中,且估價值優于closed集中的子節點Y,將closed集中的子節點Y移除,并將子節點Y加入open優先隊列。
4、將節點X放入closed集中。
5、重復過程2,3,4直到目標節點找到,或者open為空,程序結束。

BFS不能保證找到一條最短路徑。然而,它比Dijkstra算法快的多,因為它用了一個啟發式函數(heuristic function)快速地導向目標結點。
這篇博客對BFS進行了詳細的介紹用的是羅馬尼亞度假問題
https://blog.csdn.net/weixin_46582817/article/details/115217489
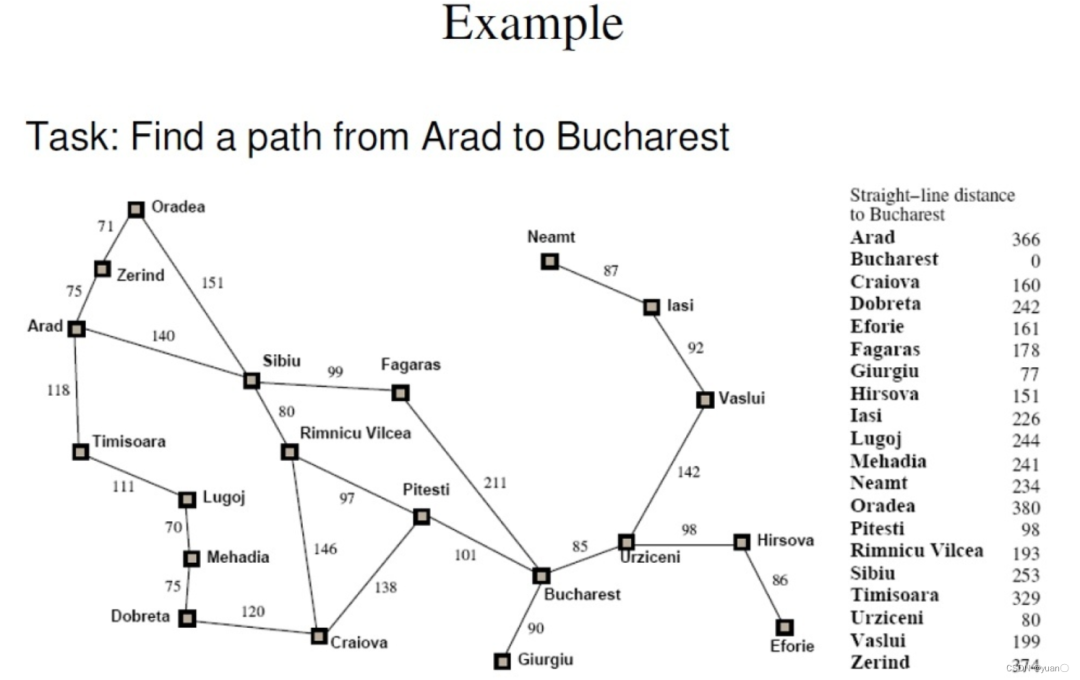
2. A-Star算法
1968年發明的A*算法就是把啟發式方法(heuristic approaches)如BFS,和常規方法如Dijsktra算法結合在一起的算法。
A-Star算法是一種靜態路網中求解最短路徑最有效的直接搜索方法,也是解決許多搜索問題的有效算法。
??和Dijkstra一樣,A*能用于搜索最短路徑。
??和BFS一樣,A*能用啟發式函數引導它自己。
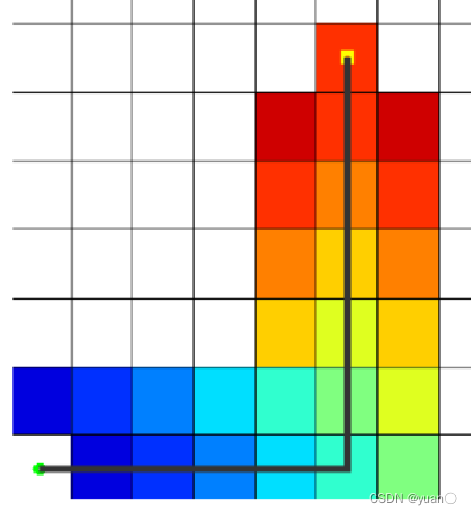
左圖為Astar算法效果圖,右圖為Dijkstra算法效果圖

Astar算法與Dijkstra算法的效果差不多,但Astar算法訪問的節點數明顯比Dijkstra算法少得多,說明其速度更快,運行時間更短。
2.1 Astar算法所屬分類
A*算法在最短路徑搜索算法中分類為:
??直接搜索算法:直接在實際地圖上進行搜索,不經過任何預處理;
??啟發式算法:通過啟發函數引導算法的搜索方向;
??靜態圖搜索算法:被搜索的圖的權值不隨時間變化(后被證明同樣可以適用于動態圖的搜索 )
2.2 Astar算法基本概念
A*算法啟發函數表示為: f(n)=g(n)+h(n)
?f(n) 是從初始狀態經由狀態n到目標狀態的代價估計
?g(n) 是在狀態空間中從初始狀態到狀態n的實際代價
?h(n) 是從狀態n到目標狀態的最佳路徑的估計代價
(對于路徑搜索問題,狀態就是圖中的節點,代價就是距離)
Astar算法是啟發式搜索算法,啟發式搜索是在狀態空間中對每一個搜索的位置進行評估,得到最好的位置,再從這個位置進行搜索直到目標。
這樣可以省略大量無謂的搜索路徑,提高效率。在啟發式搜索中,對位置的估價是十分重要的。采用了不同的估價可以有不同的效果。
啟發函數(Heuristics Function)(估價函數):?H為啟發函數,也被認為是一種試探。
由于在找到唯一路徑前,不確定在前面會出現什么障礙物,計算H的算法(例如,H可采用傳統的曼哈頓距離)具體根據實際場景決定
父節點(parent):?在路徑規劃中用于回溯的節點。
搜索區域(The Search Area):?前面圖中的搜索區域被劃分為了簡單的二維數組,數組每個元素對應一個小方格,也可以將區域等分成是五角星,矩形等,通常將一個單位的中心點稱之為搜索區域節點(Node)。
開放列表(Open List): 將路徑規劃過程中待檢測的節點存放于Open List中。
關閉列表(Close List):?將路徑規劃過程中已經檢查過的節點放在Close List。
2.3 啟發函數單調性的推導
單調性:單調性是Astar算法非常重要的一個性質,它決定了在用Astar算法進行路徑搜索時,一定能找到一條最優路徑。
設父節點的坐標為(x0,y0),它的任意一個子節點的坐標為(xi,yi),所以對兩者之間的h(x),就一定滿足

在Astar算法的運行過程中,后繼的f(x)值時大于當前f(x)的值,即f(x)在之后對子節點的搜索擴展是單調遞增的,不會像人工勢場法一樣出現局部極小值,因此使用Astar算法規劃出的路徑一定是最優路徑.
2.4 設計代價函數時所需注意的點
在使用A*算法的過程中,啟發代價的值必須盡量接近于真實值(盡量選取能取到的最大值,這樣可以提升搜索效率),以保證規劃出的路徑盡可能地與實際地圖環境相符合。
根據所需的模型選擇不同的啟發代價的計算方法時,同樣必須保證啟發代價所得的估計值小于真實值。
2.5 代價函數的選擇
2.5.1 曼哈頓距離
曼哈頓距離函數在標準坐標系中,表示起始和目標兩節點的絕對值總和,其估計值就是從當前點做水平和垂直運動,到達目標點的成本的估計,因此,曼哈頓距離函數中,兩點的距離如下
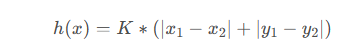
K——相鄰兩節點之間的距離,即單位距離; (x1,y1)——起始節點的坐標; (x2,y2)——目標節點的坐標;
2.5.2 歐幾里得距離
歐幾里得距離又稱為歐式距離,它是衡量兩點之間距離遠近的最常用的方法之一。歐幾里得距離函數的值可以直接看作起始節點和目標節點,在歐式空間中的直線距離,其表達式如下所示

K——相鄰兩節點之間的距離,即單位距離; (xi,yi)——當前節點的坐標; (xk,yk)——目標節點的坐標;

歐幾里德距離函數作為啟發代價的計算方法時,雖然尋徑時搜索空間增加從而導致搜索效率的降低,但其所得的估計值最小;
而在使用曼哈頓距離函數時,雖然尋徑需要遍歷的柵格空間少于歐幾里得距離函數,搜索效率較高,但這種方法得到的估計值與歐幾里得距離函數相比,距離真實值更遠。
2.6 確定最終路徑
已經確定了目標節點的坐標為,根據此目標節點的位置,和先前設置的方向存儲函數之中的方向,從目標節點利用方向反推至起始節點。具體實現的示意圖如下
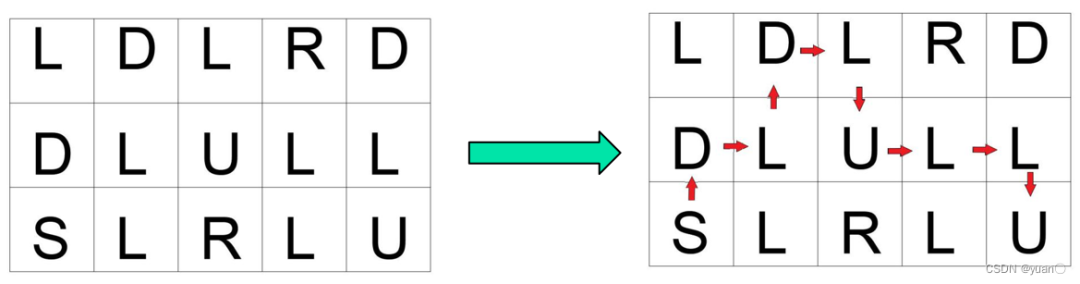
2.7 路徑平滑
我們需要對規劃出的路徑進行平滑處理,將路徑的轉折處轉化為平滑的曲線,使之更加符合無人車的實際運動路徑。
主要有基于B樣條曲線的路徑優化方法,基于Dubins圓的路徑優化方法,和基于Clothoid曲線的路徑優化方法,基于貝塞爾曲線的路徑平滑算法。
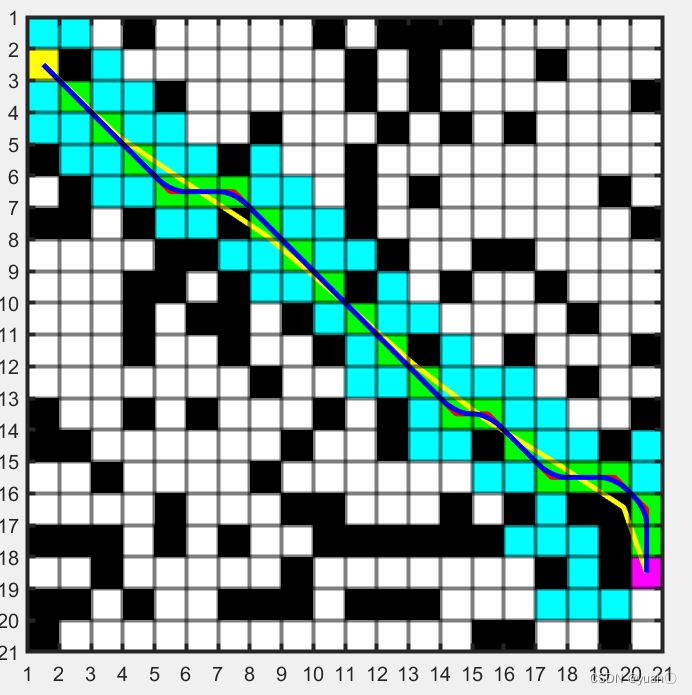
紅色為未平滑路徑,綠色方塊為最終路徑,黃色為貝塞爾曲線擬合得到,藍色為spcrv函數平滑得到。
2.8 Astar算法的優缺點
優點:
相對于需要將所有節點展開搜尋的算法,A*算法最大的優點就是引入了啟發信息作為向目標點移動的決策輔助,所以不再需要遍歷整個地圖,降低了計算復雜度,減少了時間損耗少。
缺點:
基于柵格法來分割地圖,精度越高,柵格分的就越小,就會使工作量幾何式的增長。
估價函數選取的不合理也有可能導致無法規劃出最優路徑。
距離估計與實際值越接近,估價函數取得就越好。估價函數f(n)在g(n)一定的情況下,會或多或少的受距離估計值h(n)的制約,節點距目標點近,h值小,f值相對就小,能保證最短路的搜索向終點的方向進行,明顯優于Dijkstra算法的毫無方向的向四周搜索。
2.9 Astar算法流程
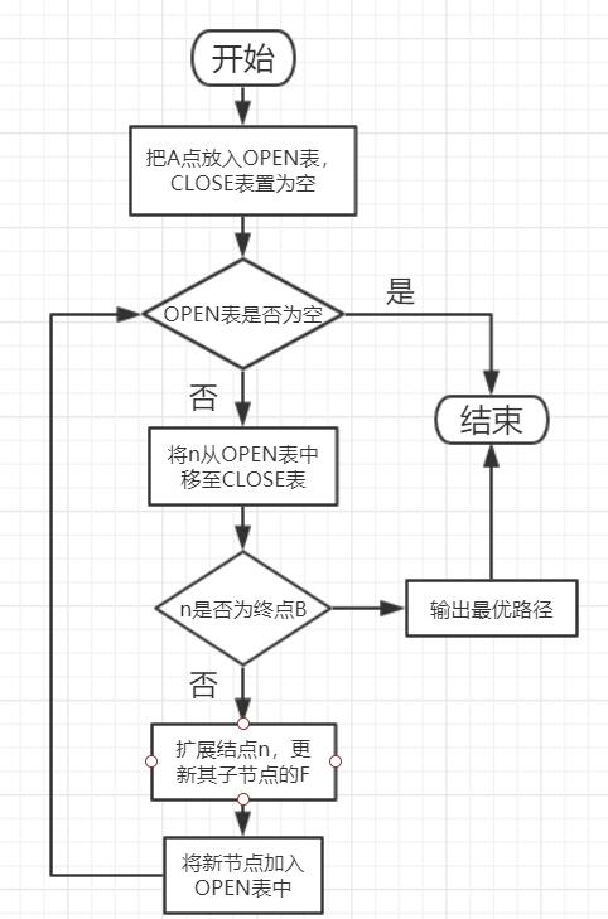
如下圖所示,綠色是起點A,紅色是終點B,一系列藍色是障礙物,從A移動到B,繞過障礙。
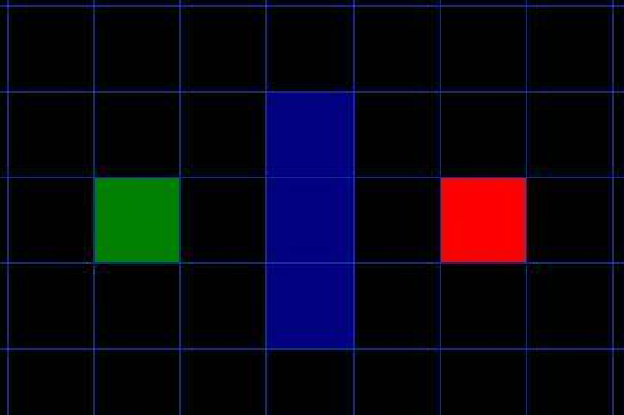
1、用方格(三角形、五角形)劃分空間,簡化搜索區域。空間被劃分為二維數組,數組中每個元素代表空間中的一個方格,可被標記為可行或不可行。未來的路徑就是一系列可行方塊的集合。Nodes的概念涵蓋了一系列可行方塊(或其它方塊)
2、將起點A放到Openlist中,Openlist存放著一系列需要檢查的節點(方塊)
3、給Openlist中每個節點賦值F=G+H (起點為0,橫向和縱向的移動代價為 10 ,對角線的移動代價為 14)
4、檢查Openlist,選取F值最小的節點(此處為A點)。
5、將A點從Openlist中刪除,放入Closelist中(Closelist中存放不可尋點,即已被訪問過的點),把A點臨近節點放入Openlist中,并將A點設為臨近節點的父節點。
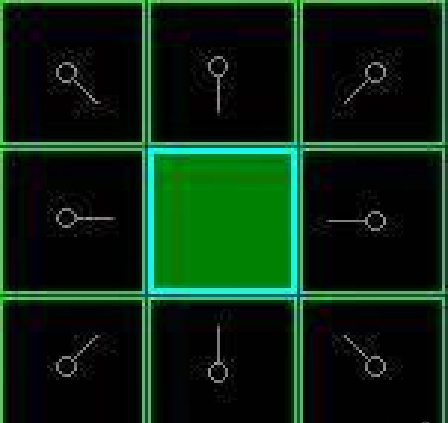
6、給Openlist中每個節點賦值,選取F值最小的節點設為當前節點Node,(若當前節點Node為終點,則尋路結束,若Openlist中沒有可尋節點,則尋路失敗)
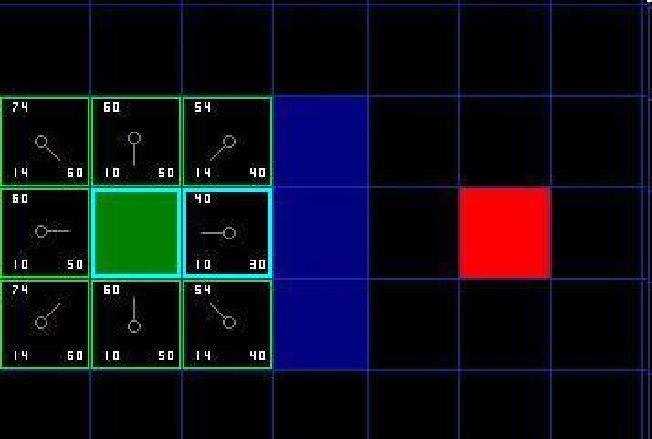
7、檢查當前節點Node周圍臨近節點。忽略Closelist中的節點和不可行節點(障礙),如果臨近節點在Openlist中,則對比一下是否從當前節點到臨近節點的G值比原G值(直接到臨近節點的實際代價值)小,若是,把當前節點作為父節點。否,不做改動。如果臨近節點不在Openlist中,將其加入到Openlist中,將當前節點設為它的父節點。
8、若上步驟中新節點未造成任何改動,將新節點作為當前節點,重復6,7)中的步驟,直到找到目標節點。

尋找到目標節點
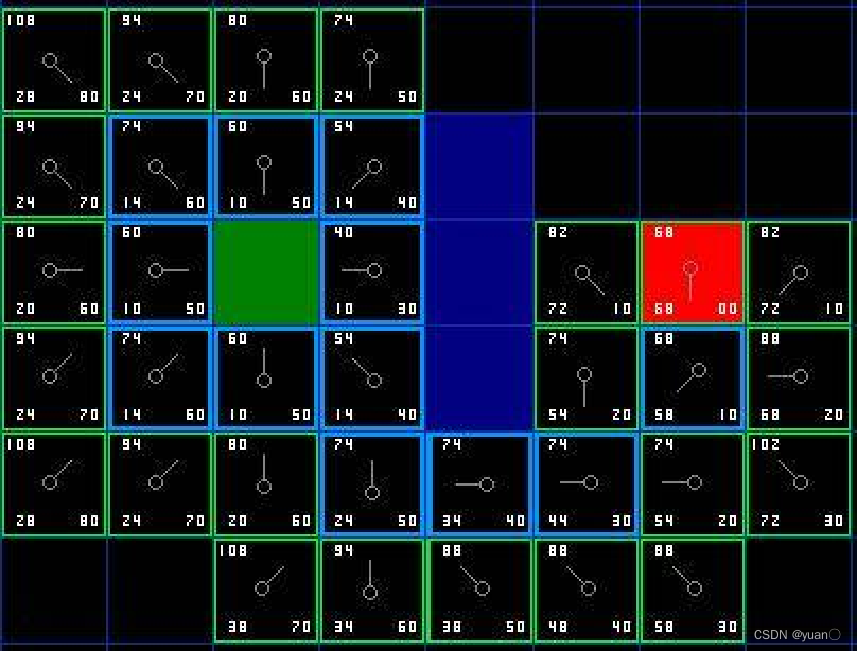
9、從目標節點回溯可以找到初始點,從而確定路徑

上述描述路徑的圖片有些錯誤,具體步驟如下圖所示。

3. 其他Astar算法
3.1 Astar——三維地圖規劃
3.1.1 3D-Astar原理
三維柵格地圖,顧名思義不是簡單的二維平面,它必須得有三維方向,也就是高度方向上的拓展。柵格地圖在XY水平面上的柵格的投影顏色不盡相同,柵格黃色程度越高,表明此處的高度越高。
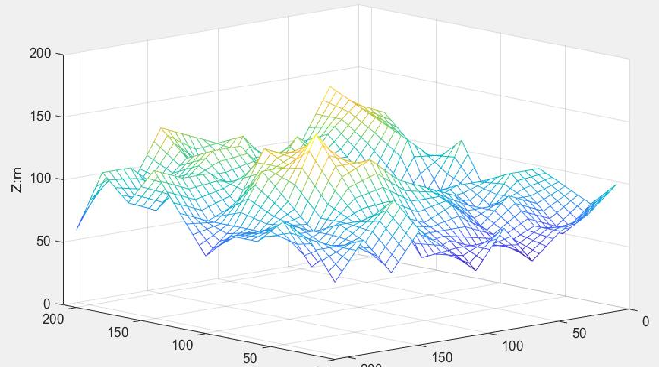
為了使啟發代價的值應該盡量接近于真實值,三維柵格地圖中仍然選用歐幾里得距離作為估價函數計算啟發代價的計算方法。
但本次實驗所處的環境為三維避障空間,因此相較于二維空間的路徑規劃,我們將公式做三維化推廣,具體形式如下:

h(n)——當前節點到目標節點的啟發代價值;
g(n-1)——當前節點到它的父節點之間的路徑代價;
D(n-1, n)——當前節點與它的子節點之間的代價值。
g(n-1)與二維規劃中的距離代價計算方法一致,但D(n-1, n)在計算時用父節點與子節點之間的距離值除以三維避障環境中設定的柵格可通行程度,h(n)也是用當前節點到目標節點的啟發代價值除以地圖環境中預先設定的柵格可通行程度。
3.1.2 基于MATLAB實現3D-Astar
這里是代碼的GitHub地址:
https://github.com/ybmasmiling/Astar_3D

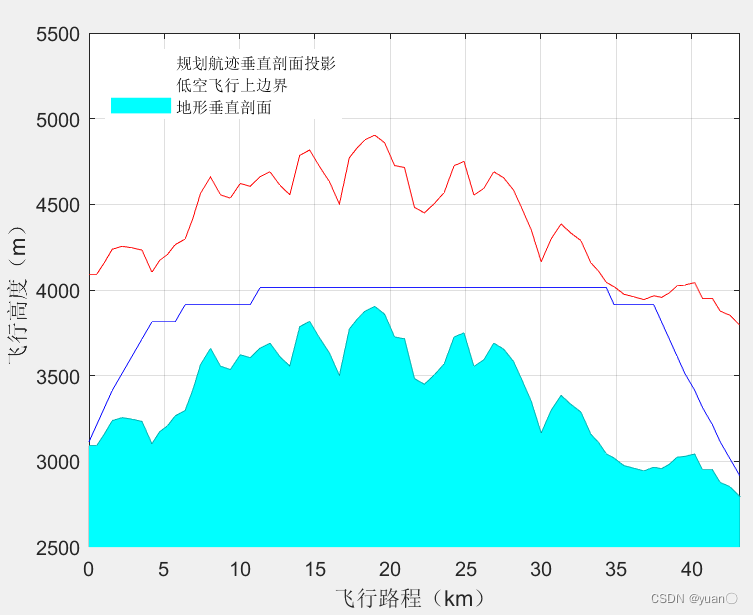
3.2 距離與能量復合Astar算法
經典Astar算法路徑規劃是取兩節點間曼哈頓距離作為距離估計為最優原則搜索路徑,從而得到最短路徑。
搜索路徑的過程中并沒有考慮實際道路坡度和道路滾動阻力系數對行駛車輛最短路徑搜索的影響,也沒有考慮在道路上行駛的能量損耗問題,即經典Astar算法搜索的最短路徑并非符合實際車輛行駛的最優路徑。
3.2.1 最短路徑啟發函數
最短路徑啟發函數:

?

最終得到的最短路徑啟發函數如下式:
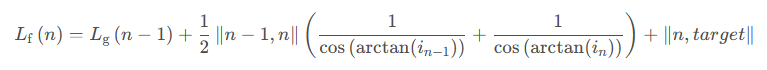
3.2.2 最短道路損耗功啟發函數
道路損耗功啟發函數:

?

最終得到的最短道路損耗功啟發函數如下式:
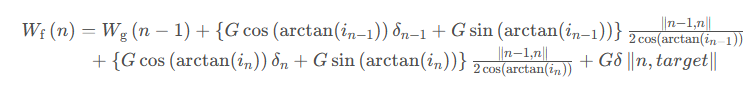
3.2.3 綜合啟發函數
綜合啟發函數:
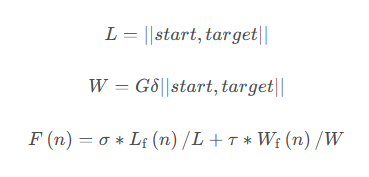
?
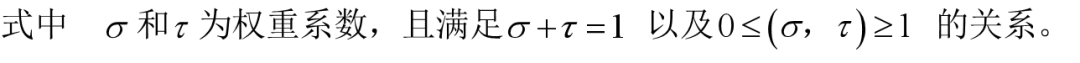
綜合式啟發函數統一最短路徑啟發函數和最小道路額外功函數,不同的權重大小決定最短路徑啟發函數和最小道路額外功函數在綜合式啟發函數中所占不同的比重。
3.3 雙向Astar算法
傳統A算法在大環境中搜索,存在著搜索效率低的問題。
傳統A算法是從起點開始向終點搜索,直到尋到可行路徑停止搜索,在搜索路徑的前期階段遠g(n)小于h(n),搜索時橫向搜索范圍窄,縱向搜索范圍寬,搜索速度快,在搜索的后期階段g(n)遠大于h(n),搜索時縱向搜索范圍窄,橫向搜索范圍寬,搜索速度慢;**而改進后的雙向A搜索算法分別從起點和終點開始搜索,當搜索到相同的當前節點時,搜索結束。
**相比于傳統A算法,雙向A*搜索算法都處于g(n)遠小于h(n)階段,一定程度上提高了算法的搜索效率,縮短搜索時間。

4. MATLAB實現Astar算法
4.1 defColorMap.m
用于初始化地圖參數
?
?
function [field,cmap] = defColorMap(rows, cols) cmap = [1 1 1; ... ? ? ? % 1-白色-空地 ? ?0 0 0; ... ? ? ? ? ? % 2-黑色-靜態障礙 ? ?1 0 0; ... ? ? ? ? ? % 3-紅色-動態障礙 ? ?1 1 0;... ? ? ? ? ? ?% 4-黃色-起始點 ? ?1 0 1;... ? ? ? ? ? ?% 5-品紅-目標點 ? ?0 1 0; ... ? ? ? ? ? % 6-綠色-到目標點的規劃路徑 ? ? ?0 1 1]; ? ? ? ? ? ? ?% 7-青色-動態規劃的路徑 % 構建顏色MAP圖 colormap(cmap); % 定義柵格地圖全域,并初始化空白區域 field = ones(rows, cols); % 障礙物區域 obsRate = 0.3; obsNum = floor(rows*cols*obsRate); obsIndex = randi([1,rows*cols],obsNum,1); field(obsIndex) = 2;
?
?
4.2 getChildNode.m
用于獲取子節點信息
?
?
function childNodes = getChildNode(field,closeList, parentNode) % 選取父節點周邊8個節點作為備選子節點,線性化坐標 % 排除超過邊界之外的、位于障礙區的、位于closeList中的 [rows, cols] = size(field); [row_parentNode, col_parentNode] = ind2sub([rows, cols], parentNode); childNodes = []; closeList = closeList(:,1); % 第1個子節點(右節點) childNode = [row_parentNode, col_parentNode+1]; if ~(childNode(1) < 1 || childNode(1) > rows ||... ? ? ? ?childNode(2) < 1 || childNode(2) > cols) ? ?if field(childNode(1), childNode(2)) ~= 2 ? ? ? ?childNode_LineIdx = sub2ind([rows, cols], childNode(1), childNode(2)); ? ? ? ?if ~ismember(childNode_LineIdx, closeList) ? ? ? ? ? ?childNodes(end+1) = childNode_LineIdx; ? ? ? ?end ? ?end end % 第2個子節點(右上節點) childNode = [row_parentNode-1, col_parentNode+1]; child_brother_node_sub1 = [row_parentNode-1, col_parentNode]; child_brother_node_sub2 = [row_parentNode, col_parentNode+1]; if ~(childNode(1) < 1 || childNode(1) > rows ||... ? ? ? ?childNode(2) < 1 || childNode(2) > cols) ? ?if field(childNode(1), childNode(2)) ~= 2 ? ? ? ?if ?~(field(child_brother_node_sub1(1), child_brother_node_sub1(2)) == 2 & field(child_brother_node_sub2(1), child_brother_node_sub2(2)) == 2) ? ? ? ? ? ?childNode_LineIdx = sub2ind([rows, cols], childNode(1), childNode(2)); ? ? ? ? ? ?if ~ismember(childNode_LineIdx, closeList) ? ? ? ? ? ? ? ?childNodes(end+1) = childNode_LineIdx; ? ? ? ? ? ?end ? ? ? ?end ? ? ?end end % 第3個子節點(上節點) childNode = [row_parentNode-1, col_parentNode]; if ~(childNode(1) < 1 || childNode(1) > rows ||... ? ? ? ?childNode(2) < 1 || childNode(2) > cols) ? ?if field(childNode(1), childNode(2)) ~= 2 ? ? ? ?childNode_LineIdx = sub2ind([rows, cols], childNode(1), childNode(2)); ? ? ? ?if ~ismember(childNode_LineIdx, closeList) ? ? ? ? ? ?childNodes(end+1) = childNode_LineIdx; ? ? ? ?end ? ?end end % 第4個子節點(左上) childNode = [row_parentNode-1, col_parentNode-1]; child_brother_node_sub1 = [row_parentNode-1, col_parentNode]; child_brother_node_sub2 = [row_parentNode, col_parentNode-1]; if ~(childNode(1) < 1 || childNode(1) > rows ||... ? ? ? ?childNode(2) < 1 || childNode(2) > cols) ? ?if field(childNode(1), childNode(2)) ~= 2 ? ? ? ?if ?~(field(child_brother_node_sub1(1), child_brother_node_sub1(2)) == 2 & field(child_brother_node_sub2(1), child_brother_node_sub2(2)) == 2) ? ? ? ? ? ?childNode_LineIdx = sub2ind([rows, cols], childNode(1), childNode(2)); ? ? ? ? ? ?if ~ismember(childNode_LineIdx, closeList) ? ? ? ? ? ? ? ?childNodes(end+1) = childNode_LineIdx; ? ? ? ? ? ?end ? ? ? ?end ? ? ?end end % 第5個子節點(左節點) childNode = [row_parentNode, col_parentNode-1]; if ~(childNode(1) < 1 || childNode(1) > rows ||... ? ? ? ?childNode(2) < 1 || childNode(2) > cols) ? ?if field(childNode(1), childNode(2)) ~= 2 ? ? ? ?childNode_LineIdx = sub2ind([rows, cols], childNode(1), childNode(2)); ? ? ? ?if ~ismember(childNode_LineIdx, closeList) ? ? ? ? ? ?childNodes(end+1) = childNode_LineIdx; ? ? ? ?end ? ?end end % 第6個子節點(左下) childNode = [row_parentNode+1, col_parentNode-1]; ? ?child_brother_node_sub1 = [row_parentNode, col_parentNode-1]; ? ?child_brother_node_sub2 = [row_parentNode+1, col_parentNode]; if ~(childNode(1) < 1 || childNode(1) > rows ||... ? ? ? ?childNode(2) < 1 || childNode(2) > cols) ? ?if field(childNode(1), childNode(2)) ~= 2 ? ? ? ?if ?~(field(child_brother_node_sub1(1), child_brother_node_sub1(2)) == 2 & field(child_brother_node_sub2(1), child_brother_node_sub2(2)) == 2) ? ? ? ? ? ?childNode_LineIdx = sub2ind([rows, cols], childNode(1), childNode(2)); ? ? ? ? ? ?if ~ismember(childNode_LineIdx, closeList) ? ? ? ? ? ? ? ?childNodes(end+1) = childNode_LineIdx; ? ? ? ? ? ?end ? ? ? ?end ? ?end end % 第7個子節點(下) childNode = [row_parentNode+1, col_parentNode]; if ~(childNode(1) < 1 || childNode(1) > rows ||... ? ? ? ?childNode(2) < 1 || childNode(2) > cols) ? ?if field(childNode(1), childNode(2)) ~= 2 ? ? ? ?childNode_LineIdx = sub2ind([rows, cols], childNode(1), childNode(2)); ? ? ? ?if ~ismember(childNode_LineIdx, closeList) ? ? ? ? ? ?childNodes(end+1) = childNode_LineIdx; ? ? ? ?end ? ?end end % 第8個子節點(右下) childNode = [row_parentNode+1, col_parentNode+1]; ? ?child_brother_node_sub1 = [row_parentNode, col_parentNode+1]; ? ?child_brother_node_sub2 = [row_parentNode+1, col_parentNode]; if ~(childNode(1) < 1 || childNode(1) > rows ||... ? ? ? ?childNode(2) < 1 || childNode(2) > cols) ? ?if field(childNode(1), childNode(2)) ~= 2 ? ? ? ? ?if ?~(field(child_brother_node_sub1(1), child_brother_node_sub1(2)) == 2 & field(child_brother_node_sub2(1), child_brother_node_sub2(2)) == 2) ? ? ? ? ? ?childNode_LineIdx = sub2ind([rows, cols], childNode(1), childNode(2)); ? ? ? ? ? ?if ~ismember(childNode_LineIdx, closeList) ? ? ? ? ? ? ? ?childNodes(end+1) = childNode_LineIdx; ? ? ? ? ? ?end ? ? ? ?end ? ?end end
?
?
4.3 Astar.m
主程序
?
?
% 基于柵格地圖的機器人路徑規劃算法 % A*算法 clc clear close all %% 柵格界面、場景定義 % 行數和列數 rows = 20; cols = 20; [field,cmap] = defColorMap(rows, cols); % 起點、終點、障礙物區域 startPos = 2; goalPos = rows*cols-2; field(startPos) = 4; field(goalPos) = 5; %% 預處理 % 初始化closeList parentNode = startPos; closeList = [startPos,0]; % 初始化openList openList = struct; childNodes = getChildNode(field,closeList,parentNode); for i = 1:length(childNodes) ? ?[row_startPos,col_startPos] = ind2sub([rows, cols],startPos); ? ?[row_goalPos,col_goalPos] = ind2sub([rows, cols],goalPos); ? ? ?[row,col] = ind2sub([rows, cols],childNodes(i)); ? ?% 存入openList結構體 ? ?openList(i).node = childNodes(i); ? ?openList(i).g = norm([row_startPos,col_startPos] - [row,col]); ?% 實際代價采用歐式距離 ? ?openList(i).h = abs(row_goalPos - row) + abs(col_goalPos - col); ?% 估計代價采用曼哈頓距離 ? ?openList(i).f = openList(i).g + openList(i).h; end % 初始化path for i = 1:rows*cols ? ?path{i,1} = i; ?% 線性索引值 end for i = 1:length(openList) ? ?node = openList(i).node; ? ?path{node,2} = [startPos,node]; end %% 開始搜索 % 從openList開始搜索移動代價最小的節點 [~, idx_min] = min([openList.f]); ? parentNode = openList(idx_min).node; % 進入循環 while true ? ? ? ? ?% 找出父節點的8個子節點,障礙物節點用inf, ? ?childNodes = getChildNode(field, closeList,parentNode); ? ? ? ?% 判斷這些子節點是否在openList中,若在,則比較更新;沒在則追加到openList中 ? ?for i = 1:length(childNodes) ? ? ? ? ? ? ? ?% 需要判斷的子節點 ? ? ? ?childNode = childNodes(i); ? ? ? ?[in_flag,idx] = ismember(childNode, [openList.node]); ? ? ? ? ? ? ? ? ?% 計算代價函數 ? ? ? ?[row_parentNode,col_parentNode] = ind2sub([rows, cols], parentNode); ? ? ? ?[row_childNode,col_childNode] = ind2sub([rows, cols], childNode); ? ? ? ?[row_goalPos,col_goalPos] = ind2sub([rows, cols],goalPos); ? ? ? ?g = openList(idx_min).g + norm( [row_parentNode,col_parentNode] -... ? ? ? ? ? ?[row_childNode,col_childNode]); ? ? ? ?h = abs(row_goalPos - row_childNode) + abs(col_goalPos - col_childNode); % 采用曼哈頓距離進行代價估計 ? ? ? ?f = g + h; ? ? ? ? ? ? ? ?if in_flag ? % 若在,比較更新g和f ? ? ? ? ? ? ? ? ? ?if f < openList(idx).f ? ? ? ? ? ? ? ?openList(idx).g = g; ? ? ? ? ? ? ? ?openList(idx).h = h; ? ? ? ? ? ? ? ?openList(idx).f = f; ? ? ? ? ? ? ? ?path{childNode,2} = [path{parentNode,2}, childNode]; ? ? ? ? ? ?end ? ? ? ?else ? ? ? ? % 若不在,追加到openList ? ? ? ? ? ?openList(end+1).node = childNode; ? ? ? ? ? ?openList(end).g = g; ? ? ? ? ? ?openList(end).h = h; ? ? ? ? ? ?openList(end).f = f; ? ? ? ? ? ?path{childNode,2} = [path{parentNode,2}, childNode]; ? ? ? ?end ? ?end ? ? ? ? ?% 從openList移出移動代價最小的節點到closeList ? ?closeList(end+1,: ) = [openList(idx_min).node, openList(idx_min).f]; ? ?openList(idx_min)= []; ? ?% 重新搜索:從openList搜索移動代價最小的節點 ? ?[~, idx_min] = min([openList.f]); ? ?parentNode = openList(idx_min).node; ? ? ? ?% 判斷是否搜索到終點 ? ?if parentNode == goalPos ? ? ? ?closeList(end+1,: ) = [openList(idx_min).node, openList(idx_min).f]; ? ? ? ?break ? ?end end %% 畫路徑 % 找出目標最優路徑 path_target = path{goalPos,2}; for i = 1:rows*cols ? ? if ~isempty(path{i,2}) ? ? ? ?field((path{i,1})) = 7; ? ? end end field(startPos) = 4; field(goalPos) = 5; field(path_target(2:end-1)) = 6; % 畫柵格圖 image(1.5,1.5,field); grid on; set(gca,'gridline','-','gridcolor','k','linewidth',2,'GridAlpha',0.5); set(gca,'xtick',1:cols+1,'ytick',1:rows+1); axis image; hold on; [y0,x0] = ind2sub([rows,cols], path_target); y = y0 + 0.5; x = x0 + 0.5; plot(x,y,'-','Color','r','LineWidth',2.5); hold on; points = [x',y']; M = 10; [x1,y1] = bezir_n(points, M); plot(x1,y1,'-','Color','y','LineWidth',2.5); hold on; values = spcrv([[x(1) x x(end)];[y(1) y y(end)]],3); plot(values(1,:),values(2,:),?'b','LineWidth',2.5);
?
?
4.4 算法效果
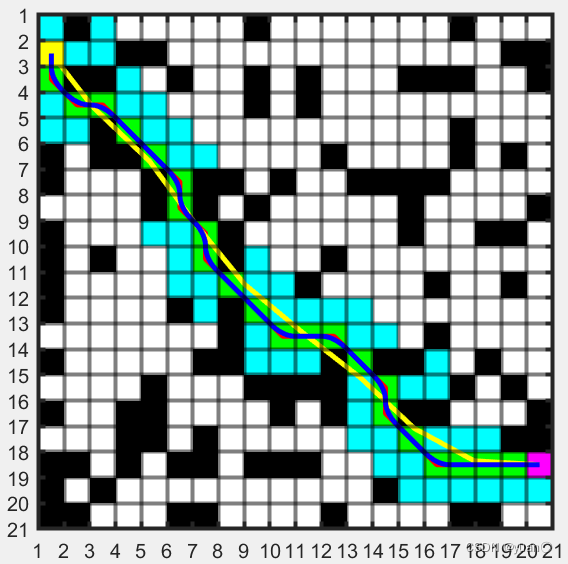
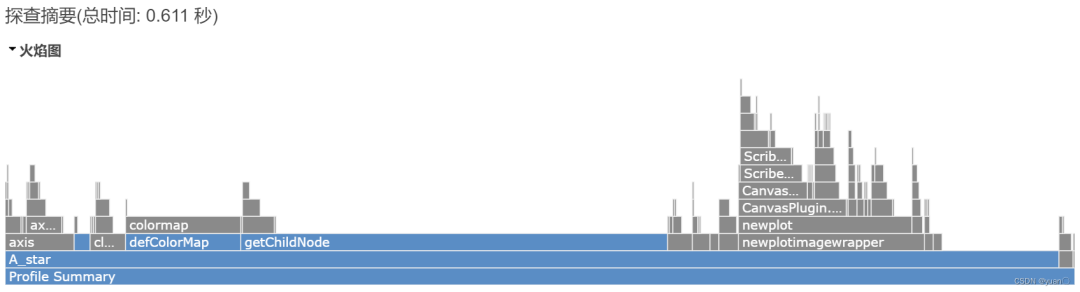
運行總時間

柵格地圖大小(20x20)
柵格地圖大小(30x30)

柵格地圖大小(40x40)
可以看到Astar算法對于柵格地圖越大的情況,搜索時間越長,其速度相比Dijkstra有優勢(尤其是在地圖比較大的時候,優勢更明顯)。
但其總耗時較長,不適用于實時的路徑規劃,不適用于局部路徑規劃,適用于全局路徑規劃。
5. python實現Astar算法
可以參考這篇文章
https://www.jianshu.com/p/5704e67f40aa
這篇文章介紹了Astar以及后續的變種算法
python 版本的偽代碼(來源:https://brilliant.org/wiki/a-star-search/)如下:
?
?
make an openlist containing only the starting node make an empty closed list ? while (the destination node has not been reached): ? ? ? consider the node with the lowest f score in the open list ? ? ? if (this node is our destination node) : ? ? ? ? ? we are finished ? ? ? if not: ? ? ? ? ? put the current node in the closed list and look at all of its neighbors ? ? ? ? ? for (each neighbor of the current node): ? ? ? ? ? ? ? if (neighbor has lower g value than current and is in the closed list) : ? ? ? ? ? ? ? ? ? replace the neighbor with the new, lower, g value ? ? ? ? ? ? ? ? ? current node is now the neighbor's parent ? ? ? ? ? ? ? ? ? ? ? ? ? else if (current g value is lower and this neighbor is in the open list ) : ? ? ? ? ? ? ? ? ? replace the neighbor with the new, lower, g value ? ? ? ? ? ? ? ? ? change the neighbor's parent to our current node ? ? ? ? ? ? ? else if this neighbor is not in both lists: ? ? ? ? ? ? ? ? ? add it to the open list and set its g
?
?
6. Java實現Astar算法
可以參考這篇文章:
https://www.jianshu.com/p/950233af52df
7. 實踐案例—基于ROS實現Astar與DWA算法
本項目以Astar算法作為全局路徑規劃算法,DWA作為局部路徑規劃算法,實現效果如下。(具體原理與算法代碼解釋與說明會在之后的文章附上)
編輯:黃飛
?
 電子發燒友App
電子發燒友App











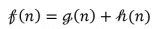











評論