???????1 引言
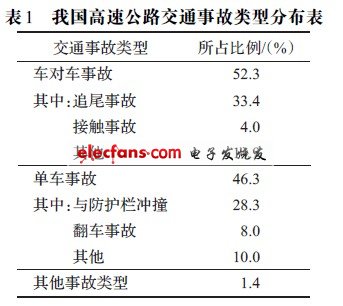
追尾碰撞是目前我國高速公路各類事故中較多的一類事故,占事故總數的33%左右。根據對沈大、合寧、廣深、西臨等高速公路交通事故的統計分析,交通事故類型如表1所示。
有關研究表明,若駕駛員能夠提早1 秒意識到有事故危險并采取相應的措施,則90%的追尾事故和60%的正面碰撞事故都可以避免。美、英、德、日的不少汽車公司(如德國的奔馳、日本的三菱、馬自達、日產、本田及富土重工等公司)都開展了高速公路車載毫米波雷達防追尾碰撞預警系統的研究。
我國主要有清華大學、浙江大學、上海交通大學、吉林大學等高校和部分研究所在進行車輛主動防撞報警、輔助駕駛系統等相關技術研究。例如上海交通大學卓斌教授等研究開發了“人—車—路綜合環境下主動安全性模擬系統”,實現了行車環境數據采集、通訊和駕駛軟件仿真的編制。在現行的高速公路交通管理中,為保證行車安全,常依據公路工程技術標準中的行車視距要求,規定一定行駛速度下的車輛必須保持相應的間距。那么如何準確跟蹤車輛之間的距離信息,就成了汽車毫米波雷達防追尾預警系統的關鍵。
把交互多模型(IMM)機動目標跟蹤算法運用到汽車毫米波雷達防追尾預警系統當中,當毫米波雷達存在一定測量誤差和噪聲時,目標跟蹤算法能使毫米波雷達能夠準確地探知前方車輛的運動狀態,如車間距離、行駛速度等,從而提高駕駛員在高速公路上行駛安全性。
2 汽車防追尾預警系統工作原理
高速公路汽車防追尾預警系統由信息采集單元、信息處理單元和信息輸出裝置3 部分組成。信息采集單元通常由毫米波雷達、自車速度傳感器、轉向角傳感器、制動傳感器、加速踏板傳感器和路面情況選擇開關等組成;信息處理單元主要為中央處理器;信息輸出裝置包括液晶顯示屏、報警蜂鳴器、報警指示燈等,圖1 是車載雷達防追尾預警系統組成方框圖。
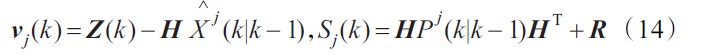
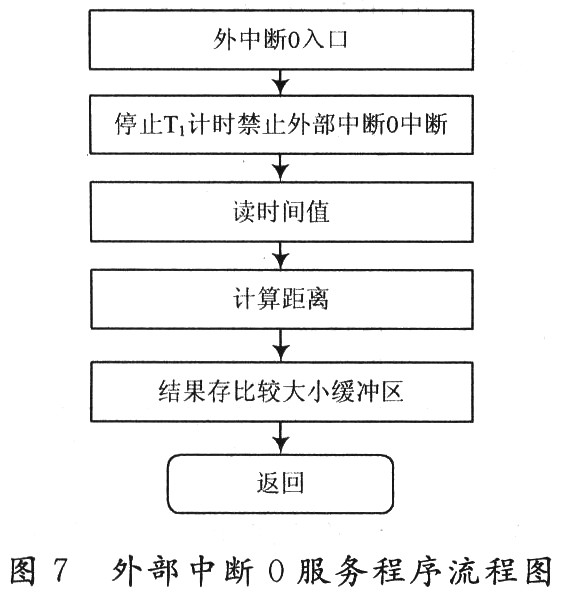
信息采集單元不斷地采集相關信息,利用車載毫米波雷達獲得前方目標車輛的運動信息,如車間距離、相對速度;利用自車傳感系統獲得自車運行狀態信息,如自車速度、有無轉向、有無制動等,并將此信息傳送至信息處理單元。信息處理單元根據自車速度、相對速度以及所建立的安全距離計算模型,計算出當前應保持的安全距離并與實測車間距離相比較。若實測車間距離大于提醒報警距離,則進入下一工作循環;若實測車間距離小于提醒報警距離,則進行一次報警,提醒駕駛員松油門并做好剎車準備;當實測車間距離小于危險報警距離,則進行二次報警,促使駕駛員立即制動,以避免追尾事故的發生。液晶顯示屏用于顯示兩車間實際距離及相對速度,報警蜂鳴器和報警指示燈用于提供聲音報警和指示燈報警,及時的報警可以有效地提醒駕駛員,促使其采取合適的應對措施。
汽車在道路上行駛時,經常要進行加速、減速和轉彎,其運動狀態是不斷改變的。行駛中的汽車所處的道路環境是相當復雜的,而安裝車載毫米波雷達的汽車本身也是不時地處于機動狀態之中,因此車載雷達所探測的目標也是在不停的變化當中,導致所測兩汽車之間的距離數據存在一定測量誤差和噪聲,就會使汽車防追尾預警系統產生虛警或漏警。過高虛警率的雷達不但不能減輕駕駛者的工作負擔,反而會造成駕駛者精神高度緊張,起到相反的效果。因此,采用合適的機動目標跟蹤算法,準確地跟蹤自車前面的車輛目標的狀態、及時估計行車的危險程度是車載雷達測距系統的一項主要任務。
3 交互多模型機動車輛跟蹤算法
交互多模算法是Blom和Bar-Shalom在多模型基礎上提出的,是在廣義偽貝葉斯算法基礎上,以卡爾曼濾波為出發點,提出的一種具有馬爾可夫切換系數的交互式多模型算法,其中多種模型并行工作,目標狀態估計是多個濾波器交互作用的結果。該算法不需要機動檢測,同時達到了全面自適應能力。IMM算法的基本思想是在每一時刻,假設某個模型在現在時刻有效的條件下,通過混合前一時刻所有濾波器的狀態估計值來獲得與這個特定模型匹配的濾波器的初始條件;然后對每個模型并行實現正規濾波(預測與修正)步驟;最后,以模型匹配似然函數為基礎更新模型概率,并組合所有濾波器修正后的狀態估計值(加權和)以得到狀態估計。一個模型有效的概率在狀態估值和協方差的加權綜合計算中有重要作用。IMM的設計參數為:不同匹配和結構的設置模型;不同模型的處理噪聲密度(一般來講,非機動模型具有低水平測量噪聲,機動模型具有較高水平的噪聲);模型之間的切換結構和轉移概率。與其他的機動目標的跟蹤算法相比,比如辛格(Singer)算法、輸入估計(IE)算法、變維濾波(VD)算法等,交互多模(IMM)算法的優點是它不需要機動檢測器監視機動[10],從而不會產生因模型在機動與非機動之間切換而帶來的誤差。其算法原理如下:
假定有r 個模型:
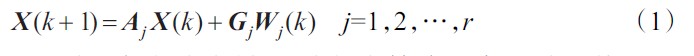
其中X(k)為目標狀態向量,Aj為狀態轉移矩陣,Gj為系統噪聲作用矩陣,Wj(k)是均值為零,協方差矩陣為Qj的白噪聲序列。
可用一個馬爾可夫鏈來控制這些模型之間的轉換,馬爾可夫鏈的轉移概率矩陣為:
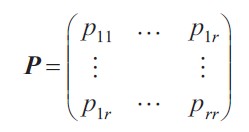
測量模型為:

其中Z(k)為量測向量,H為觀測矩陣,V(k)為量測噪聲,已知其方差為R(k)。W(k)和V(k)是零均值且相互獨立。
IMM算法可歸納如下4 個步驟。
步驟1 輸入交互:
根據兩模型(k-l)時刻的濾波值和模型概率,計算交互混合后的濾波初始值,包括模型1 的濾波初始值:濾波估計值X 01
(k - 1)和估計協方差μ1(k - 1);模型2 的濾波初始值:濾波估計值X 02
(k - 1)和估計誤差協方差P02
(k - 1)。設系統在(k-1)時刻模型1 概率為μ1(k - 1),濾波值X1
(k - 1),估計誤差協方差為P2(k - 1)。模型2 的概率為μ2(k - 1),濾波值為X 2
(k - 1),系統估計誤差協方差為P2(k - 1)。則進一步推廣到r 個模型,交互后r模型的濾波初始值為:


步驟2 模型條件濾波:
對應于模型Mj(k),以X 0j
(k - 1|k - 1),P0j(k - 1|k - 1)及Z(k)作為輸入進行卡爾曼濾波。
卡爾曼預測方程:
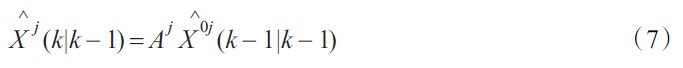
預測誤差協方差陣:
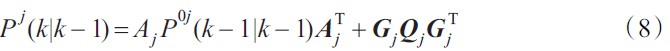
卡爾曼增益:
![]()
濾波方程為:
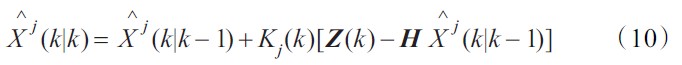
波誤差方差陣:
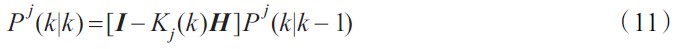
步驟3 模型概率更新:

i = 1rΛj(k)cj_,而Λj(k)為觀測Z(k)的似然函數:

其中:
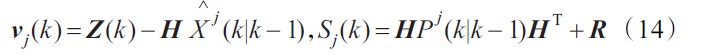
步驟4 輸出交互:


圖2 為IMM算法結構原理圖
?
4 車輛運動模型分析與IMM算法跟蹤仿真
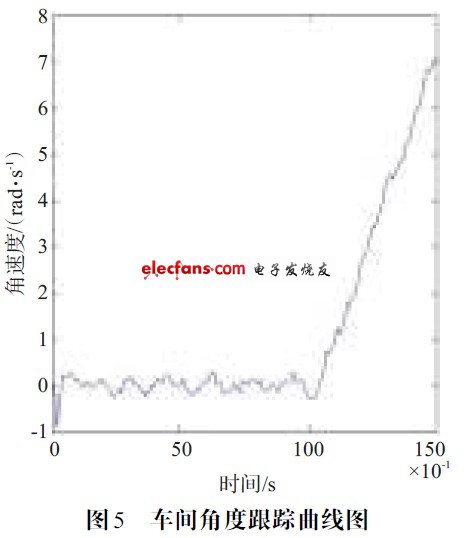
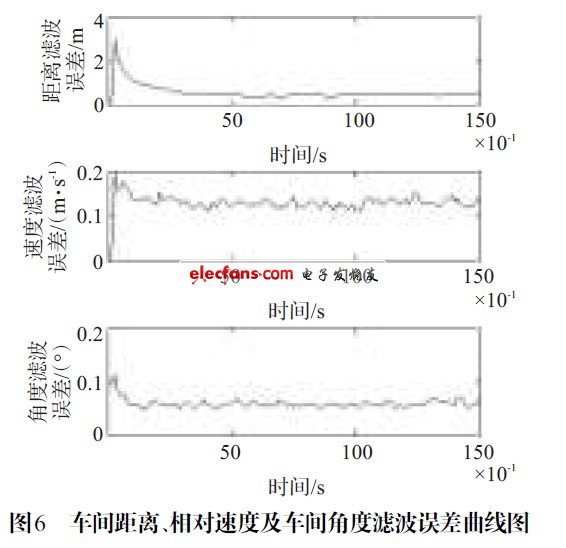
????? 實驗設計:考慮兩輛車在道路上同向行駛,在0~10 s 時,兩車均保持勻速直線運動,由安裝在后車上的車載毫米波雷達檢測出與前車的距離為100 m,相對速度為-3 m/s,方位角2°。
在10~15 s 時,前車向右偏轉,與后車的相對角加速度為1° s2。
后車加速,與前車的縱向相對加速度為a = -1.8 m/s2。雷達的掃描周期為T=0.1 s,系統噪聲為σα = 0.3 m/s,σβ = 0.3°/s。量測誤差為σ1 = 1 m?σ2 = 0.5 m/s?σ3 = 0.2°/s。
車輛勻速直線運動模型:

車輛加速運動模型:

兩種運動模型的系統噪聲向量W(k)協方差矩陣Q(k)=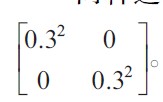
兩種運動模型的觀測模型都是Z(k) =HX(k) + V(k) 其中:

兩個模型之間的轉移概率矩陣是:

采用蒙特卡洛方法對跟蹤濾波器進行仿真分析,仿真次數為400 次。以下運用Matlab7.0 仿真的結果。
由圖3~圖6 仿真結果表明,該算法能夠有效地跟蹤前方車輛的運動信息,并且誤差較小,精度較高。
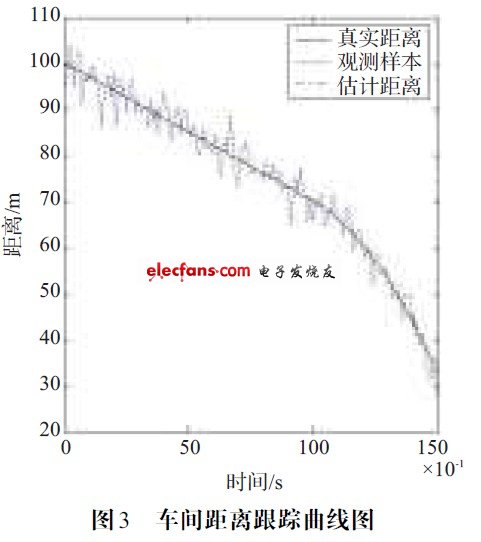
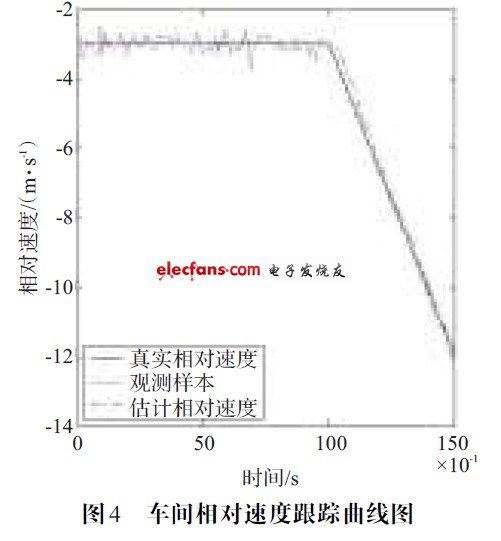
?
5 總結
重點研究了交互多模型機動目標跟蹤算法在車載毫米波雷達防追尾預警系統中的應用,介紹機動目標跟蹤算法原理和步驟,并以高速公路上行駛的汽車為對象進行防真,結果表明算法具有結構簡單、運算量小、精度較高的優點,能夠提高車載雷達防追尾預警系統的使用效率,從而提高車輛駕駛的安全性,具有一定的應用價值。
 電子發燒友App
電子發燒友App

























評論