1 RRT算法的簡(jiǎn)介

天下武功唯快不破，快是 RRT 的最大優(yōu)勢(shì)。RRT 的思想是快速擴(kuò)張一群像樹(shù)一樣的路徑以探索空間的大部分區(qū)域，找到可行的路徑。

RRT 算法是一種對(duì)狀態(tài)空間隨機(jī)采樣的算法，通過(guò)對(duì)采樣點(diǎn)進(jìn)行碰撞檢測(cè)，避免了對(duì)空間的精確建模帶來(lái)的大計(jì)算量，能夠有效地解決高維空間和復(fù)雜約束的路徑規(guī)劃問(wèn)題。

與PRM類(lèi)似，該方法是概率完備且非最優(yōu)的。可以輕松處理障礙物和差分約束（非完整和動(dòng)力學(xué)）的問(wèn)題，并被廣泛應(yīng)用于機(jī)器人路徑規(guī)劃。

2 RRT算法原理

2.1 算法流程

（1）設(shè)定初始點(diǎn)? 與目標(biāo)點(diǎn) ，自行設(shè)定狀態(tài)采樣空間?

（2）進(jìn)行隨機(jī)采樣得到采樣點(diǎn) ，如果采樣點(diǎn)? 在障礙物內(nèi)，則重新隨機(jī)采樣

（3）若不在障礙物內(nèi)，計(jì)算該采樣點(diǎn)? 與集合? (已經(jīng)生成的節(jié)點(diǎn)) 中的所有節(jié)點(diǎn)之間的距離，得到離得最近的節(jié)點(diǎn) ，再?gòu)墓?jié)點(diǎn)? 以步長(zhǎng)? 走向節(jié)點(diǎn)? ，生成一個(gè)新的節(jié)點(diǎn) ，若? 與? 的連線(xiàn)? 經(jīng)過(guò)障礙物，則重新隨機(jī)采樣

（4）經(jīng)過(guò)反復(fù)迭代，生成一個(gè)隨機(jī)擴(kuò)展樹(shù)，當(dāng)隨機(jī)擴(kuò)展樹(shù)中的子節(jié)點(diǎn)進(jìn)入了我們規(guī)定的目標(biāo)區(qū)域，便可以在隨機(jī)擴(kuò)展樹(shù)中找到一條由從初始點(diǎn)到目標(biāo)點(diǎn)的路徑。

2.2 算法偽代碼

可以將偽代碼與上述算法流程對(duì)照起來(lái)看

2.3 算法流程圖

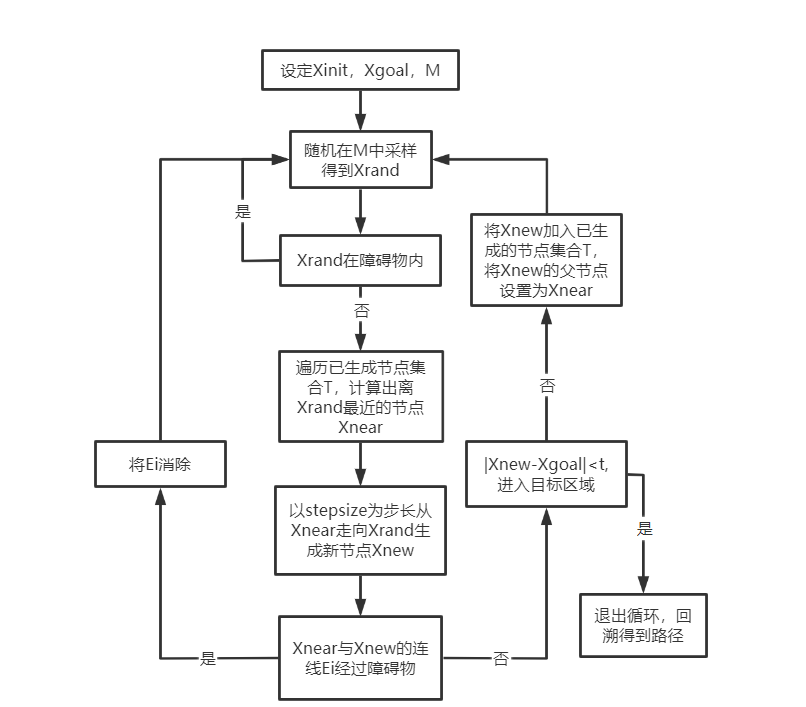
3 RRT算法matlab實(shí)現(xiàn)

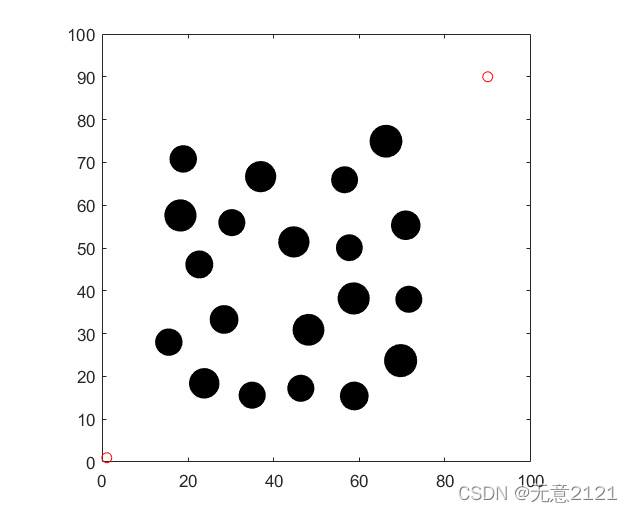
3.1 測(cè)試地圖

%隨機(jī)生成障礙物
function [f,n1]=ob(n)
f=[];%儲(chǔ)存障礙物信息
n1=n;%返回障礙物個(gè)數(shù)
p=0;
for i=1:n
 ? ?k=1;
 ? ?while(k)
 ? ? ? ?D=[rand(1,2)*60+15,rand(1,1)*1+3];%隨機(jī)生成障礙物的坐標(biāo)與半徑，自行調(diào)整
 ? ? ? ?if(distance(D(1),D(2),90,90)>(D(3)+5)) %與目標(biāo)點(diǎn)距離一定長(zhǎng)度，防止過(guò)多阻礙機(jī)器人到達(dá)目標(biāo)點(diǎn)
 ? ? ? ? ? ?k=0;
 ? ? ? ?end
 ? ? ? ?for t=1:p ?%障礙物之間的距離不能過(guò)窄，可自行調(diào)整去測(cè)試
 ? ? ? ? ? ?if(distance(D(1),D(2),f(3*t-2),f(3*t-1))<=(D(3)+f(3*t)+5))
 ? ? ? ? ? ? ? ?k=1;
 ? ? ? ? ? ?end
 ? ? ? ?end
 ? ?end
 ? ?%畫(huà)出障礙物
 ? ?aplha=0:pi/40:2*pi;
 ? ?r=D(3);
 ? ?x=D(1)+r*cos(aplha);
 ? ?y=D(2)+r*sin(aplha);
 ? ?fill(x,y,'k');
 ? ?axis equal;
 ? ?hold on;
 ? ?xlim([0,100]);ylim([0,100]);
 ? ?f=[f,D];
 ? ?p=p+1;%目前生成的障礙物個(gè)數(shù)
end
hold all;

3.2 distance函數(shù)

function f=distance(x,y,x1,y1)
 ? f=sqrt((x-x1)^2+(y-y1)^2);

3.3 RRT算法

clc
clear all
[f,n1]=ob(10);%隨機(jī)生成障礙物
Xinit=[1,1];%定義初始點(diǎn)
Xgoal=[90,90];%定義目標(biāo)點(diǎn)
plot(Xinit(1),Xinit(2),'ro');
plot(Xgoal(1),Xgoal(2),'ko');
T=[Xinit(1),Xinit(2)];%已生成節(jié)點(diǎn)集合用順序表的數(shù)據(jù)結(jié)構(gòu)存儲(chǔ)
Xnew=Xinit;
D(1)=0;%初始節(jié)點(diǎn)的父節(jié)點(diǎn)指向0
while distance(Xnew(1),Xnew(2),Xgoal(1),Xgoal(2))>3 ?%進(jìn)入目標(biāo)區(qū)域
 ? ?Xrand=round(rand(1,2)*100)+1;%狀態(tài)采樣空間：橫縱坐標(biāo)均為整數(shù)，范圍1~100
 ? ?k=1;%進(jìn)入循環(huán)
 ? ?while k==1
 ? ? ? ?k=0;%初始化采樣成功
 ? ? ? ?for i=1:n1
 ? ? ? ? ? ?if distance(Xrand(1),Xrand(2),f(i*3-2),f(i*3-1))<(f(i*3)+1)%判斷隨機(jī)采樣點(diǎn)是否在障礙物內(nèi)
 ? ? ? ? ? ? ? ?k=1;%采樣不成功
 ? ? ? ? ? ? ? ?break;
 ? ? ? ? ? ?end
 ? ? ? ?end
 ? ? ? ?Xrand=round(rand(1,2)*100);%重新采樣
 ? ?end
 ? ?min=10000;
 ? ?for i=1:size(T,2)/2 %遍歷已生成節(jié)點(diǎn)集合
 ? ? ? ?if distance(T(2*i-1),T(2*i),Xrand(1),Xrand(2))Xnew(1)
 ? ? ? ?caiyang=-0.001;
 ? ?else
 ? ? ? ?caiyang=0.001;
 ? ?end
 ? ?for i=Xnear(1)Xnew(1)%均勻采樣進(jìn)行碰撞檢測(cè)
 ? ? ? ?for j=1:n1
 ? ? ? ? ? ?if distance(f(3*j-2),f(3*j-1),i,Xnear(2)+(i-Xnear(1))/(Xnew(1)-Xnear(1))*(Xnew(2)-Xnear(2)))<=(f(3*j)+1)
 ? ? ? ? ? ? ? ?t=1;%代表碰撞
 ? ? ? ? ? ? ? ?break;
 ? ? ? ? ? ?end
 ? ? ? ?end
 ? ? ? ?if t==1
 ? ? ? ? ? ?break;
 ? ? ? ?end
 ? ?end
 ? ?if t==0
 ? ? ? ?T=[T,Xnew(1),Xnew(2)];
 ? ? ? ?for i=1:size(T,2)/2 %遍歷已生成節(jié)點(diǎn)集合
 ? ? ? ? ? ?if (T(i*2-1)==Xnear(1))&&(T(i*2)==Xnear(2)) ?%得到最近的節(jié)點(diǎn)的索引
 ? ? ? ? ? ? ? ?D(size(T,2)/2)=i;%記錄父節(jié)點(diǎn)
 ? ? ? ? ? ? ? ?break;
 ? ? ? ? ? ?end
 ? ? ? ?end
 ? ? ? ?plot([Xnew(1),Xnear(1)],[Xnew(2),Xnear(2)],'b-');hold on;pause(0.005);
 ? ? ? ?plot(Xnew(1),Xnew(2),'r.');xlim([0,100]);ylim([0,100]);
 ? ?end
end
i=size(T,2)/2;
jg=[i];
while D(i)
 ? ?i=D(i); %通過(guò)鏈表回溯
 ? ?if D(i)~=0
 ? ? ? ?jg=[D(i),jg];%存儲(chǔ)最短路徑通過(guò)的節(jié)點(diǎn)
 ? ?end
end
Fx=T(jg(1)*2-1);Fy=T(jg(1)*2);
i=2;
while jg(i)~=size(T,2)/2
 ? ?x=T(jg(i)*2-1);
 ? ?y=T(jg(i)*2);
 ? ?plot([x,Fx],[y,Fy],'g-');hold on;pause(0.05);
 ? ?Fx=x;Fy=y;
 ? ?i=i+1;
end
 plot([T(jg(i)*2-1),Fx],[T(jg(i)*2),Fy],'g-');hold on;pause(0.05);

3.4 動(dòng)畫(huà)效果

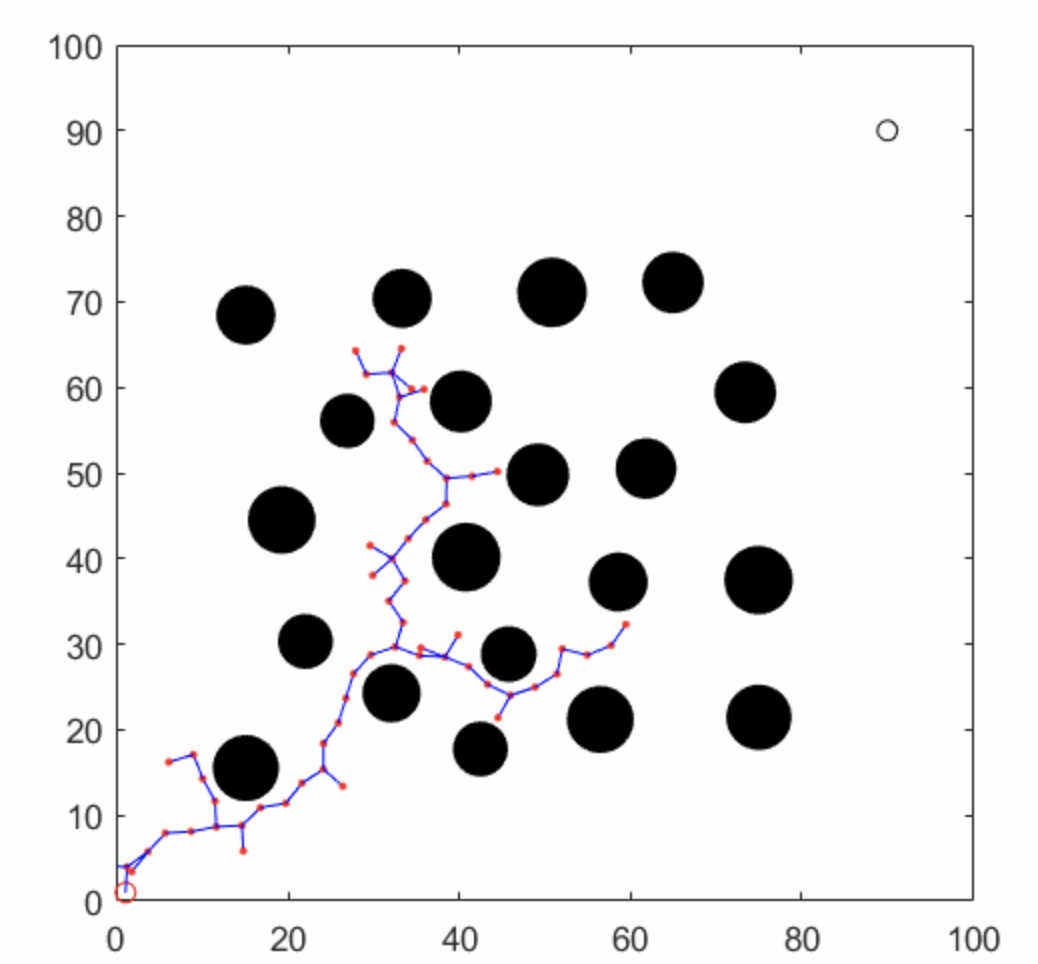
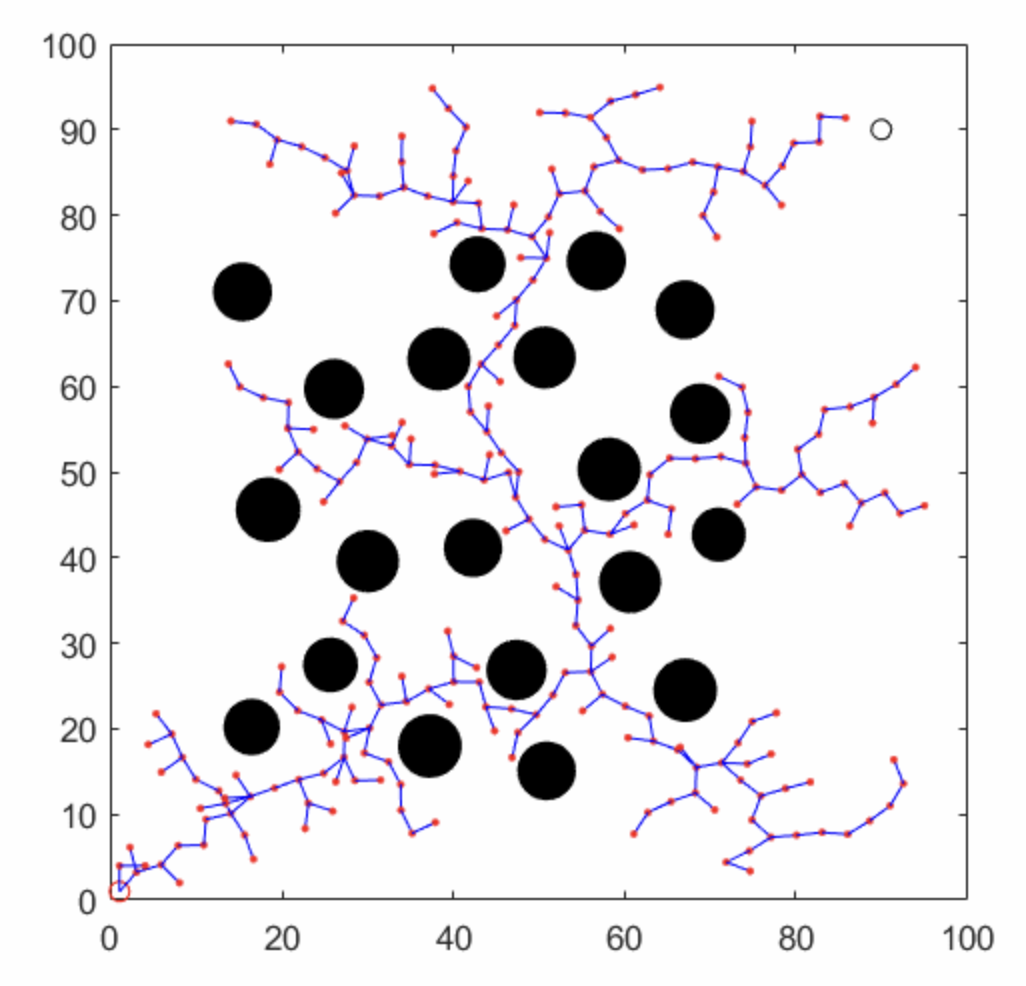
4 RRT的缺陷

（1）很明顯RRT算法得到的路徑不是最優(yōu)的

（2）RRT算法未考慮運(yùn)動(dòng)學(xué)模型

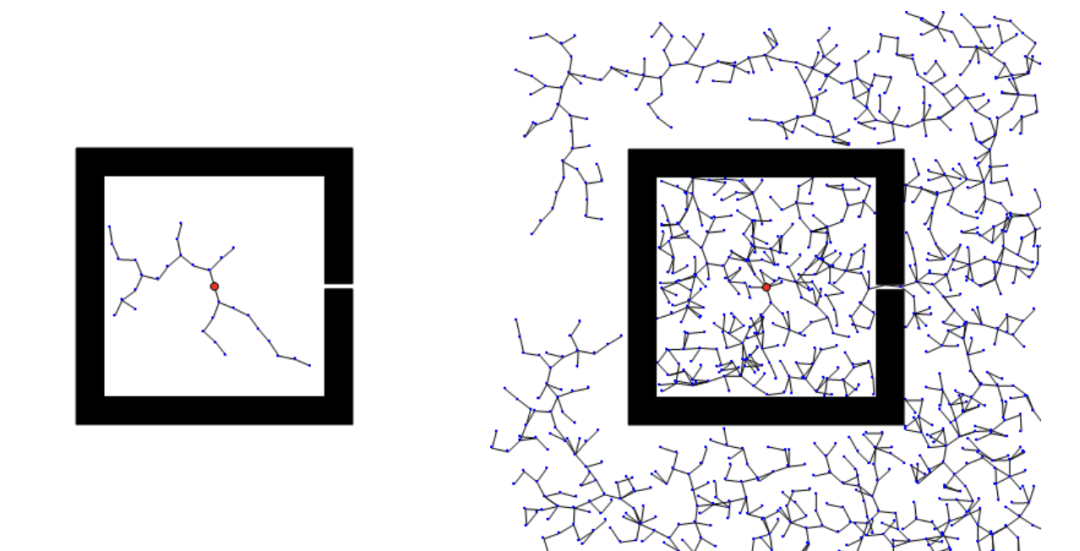
（3）RRT算法對(duì)于狹小的通道的探索性能不好，如下圖的對(duì)比，有可能探索不到出口

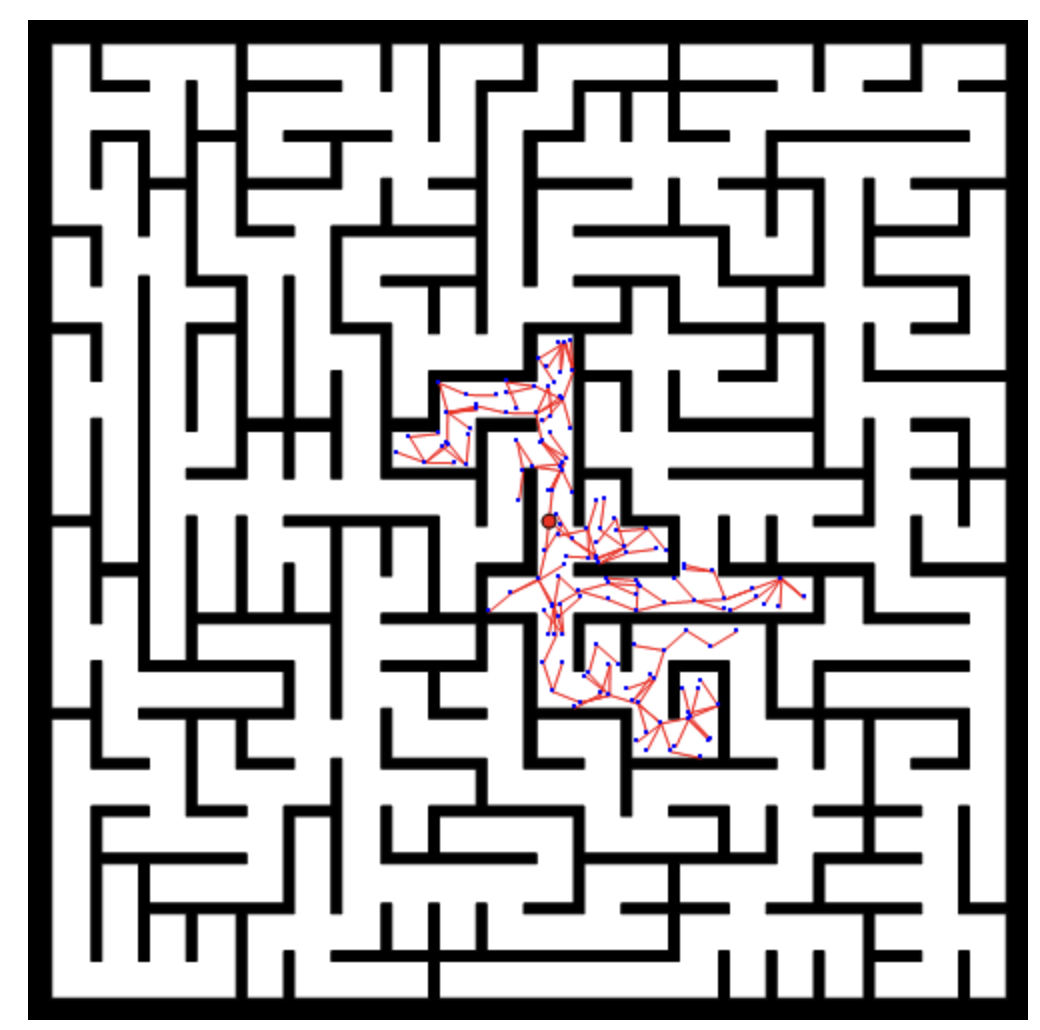
（4）沒(méi)有啟發(fā)信息的RRT像無(wú)頭蒼蠅，探索空間完全靠運(yùn)氣，如下圖

針對(duì)上述缺陷，又出現(xiàn)了很多RRT算法的變種，以后的文章中會(huì)介紹。

編輯：黃飛

?