當數據在傳送中出錯，且錯幀被漏檢時，就意味著錯誤的數據被送到應用層，除非應用層有額外的數據識別措施，這個數據就可能引起不可預測的結果。CAN協議聲稱有很低的錯幀漏檢率（4.7×10-11×出錯率），有的宣傳材料在一定條件下推出要1000年才有1次漏檢，這是不正確的。錯幀漏檢率是一個十分重要的指標，很多應用就是看到Bosch CAN2.0規范上的說明才選用CAN的。但是對這個指標的來源僅有極少的公開資料，以及很少的討論，使用戶很難對它確認或驗證，這給用戶帶來風險。本文采用了重構出錯漏檢實例的方法，導出了CAN的漏檢錯幀概率下限，它比CAN聲稱的要大幾個數量級。在許多應用中，CAN已是可靠性和價格平衡下的不二選擇，或者已被長期生產和使用，面對這個新發現的問題，在CAN本身未作改進之前，迫切需要一種“補丁”來加以改善。由于篇幅有限，所以只能摘要介紹錯幀漏檢率的推導過程，重點在提供解決方案。

　　1 關于CAN漏檢錯幀概率文獻的討論

　　Bosch CAN2.0規范說它的漏檢錯幀概率小于錯幀率（message error rate）×4.7×10-11。它的來源見參考文獻，其中沒有提供產生漏檢的分析算法，僅提到用大量仿真得到了公式。要判斷一個幀出錯后是否會漏檢，至少要計算2次CRC，對每一bit僅就匯編語言也需要幾條指令，以該文考慮的80～90 bit的幀，CRC覆蓋58～66 bit就要循環58～66次，以1989年時常用的PDP11或VAX機，一條機器指令要0.1 μs左右，一幀的判斷要0.07 ms，即使不停機做一年，能作2.20×1011幀，考慮58 bit可構成258=2.88×1017種不同的幀，再加有58×57種不同的加入2位bit錯的位置組合，所以能作的仿真只是可能情況的微乎其微的一部分（百萬分之一）。由于樣本太小，歸納的公式也就很難把影響因素考慮完整。

　　1999年Tran對錯幀漏檢率也作了研究，鑒于分析困難，他也采用計算機大量仿真的辦法，針對11位ID 、8字節數據幀，他用的是600 MB的Alpha服務器。與上述討論一樣，雖然仿真量很大，仍然是可能情況的極小部分。

　　CAN有關的另一個標準CANopen Draft Standard 304 （2005）給出的錯幀漏檢率是（7.2×10-9）。同樣來自CAN自動化協會的不同數據，使人無可適從。

　　2 新錯幀漏檢率的導出

　　本文的研究方法是構造出漏檢的實例，確定該種實例占可能的幀的概率，乘以與該實例相應的出多位錯的概率，然后求出所有可能的實例，得到CAN的錯幀漏檢率。本文對最有可能造成漏檢的二位錯情況進行分析，然后擴大為有多位錯。數據域取8字節，并假定錯都發生在數據域內。它并沒有將超過CRC校驗能力時的分散的多bit錯漏檢率考慮進去，所以得到的是漏檢錯幀概率的下界。

　　2.1 CAN位填充中有錯時的位序錯開

　　在有可能產生填充的位流中有bit錯時，就有可能造成發送方與接收方只有一方執行填充規則，造成填充位與信息位理解的錯亂。圖1（a）的第3位傳送中出錯，結果發送方的填充位1被接收方誤讀為數據1，整個接收數據比發送數據長了1位。圖1（b）的第3位傳送中的錯使接收方產生了刪除填充位的條件，因此它把發送的數據1刪去，接收數據流短了1位。

　　圖1 CAN的位填充規則使出錯后接收位流變化

　　從位流變化可以知道，如果發生的2個bit錯正好一次是圖1（a）的類型，一次是圖1（b）的類型，那么發送數據流和接收數據流的長度將仍然相等，如果2個錯都發生在數據域，CAN的其他檢驗是發現不了它們的。

　　2.2 發生漏檢的條件

　　發送的位流與接收的位流可寫為多項式形式Tx（x）和Rx（x），CRC檢驗就是用CAN的生成多項式G（x）除這2個式子，得到的余數稱為CRC值，如果2個余數相同，CRC檢驗通過。當發生傳送錯誤，Rx （x）= Tx（x）+U（x）×G（x）時，對Tx（x）和Rx（x）求到的余數是相同的，這時就發生了錯幀的漏檢。因此只要找到U（x），就可以構造出漏檢的實例。

　　2.3 由Ec（x）尾部確定漏錯多項式U（x）

　　為了使讀者了解推導過程的合理性，以下是舉例。在前面已經發生過圖1（b）的錯后，Tx的i位被Rx收到為第i-1位。尾部發生的錯對應圖1（a）的情況如圖2所示。圖中Tx的這6位構成漏檢實例的尾部，第1位1用于隔離前面位值的影響，使后面5位0后一定產生填充位。由于傳送中有錯，Rx不再有連續5位 0。Tx的填充位被Rx視為數據位，Rx和Tx就對齊，在此以后的傳送不再有位序錯。由bit錯發生位置的不同，Rx也不同，錯誤序列Ec也不同。這個 Ec也是整個錯誤序列的尾部，用Ec，t表示。由圖2可以看到，共有5種不同的錯誤序列尾部。顯然，將Tx中的0/1取反并不改變錯誤序列尾部Ec，t的形式。

　　圖2 第2個傳送錯造成填充位誤讀為信息位的5種漏檢錯序列尾部形式

　　在已知錯誤序列尾部形式Ec，t后便可以求出滿足它的漏錯多項式尾部Ut。將各多項式的系數表示為：

　　為滿足Ec，t=G×Ut的尾部，那么系數有如下關系：

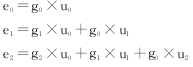
　　實際上將Ec，t、G均作逆序排列：

　　類似于求CRC值時的方法，將Ec，tR×x5除以GR就可以得到Ut的逆序系數，也就得到了Ut。由CAN生成多項式G的系數（1100，0101，1001，1001）以及Ec，t系數便得到了滿足錯誤序列尾部形式的漏錯多項式Ut，如表1所列。

　　表1 錯誤序列尾部形式和漏錯多項式Ut（x）

　　2.4 Ut的擴充形成Ec頭部

　　在Ut中增加高于x5的項成為U，它不會影響Ec尾部的形式，但是它會增加錯誤序列的長度。由此U生成的Ec與Tx序列也將被漏檢。Tx在數據域內不同位置的集合就構成了所有漏檢實例。發生第一次bit錯后并不立即開始Tx?Rx位序的錯位，要等到有填充位發生時才會有位序錯。

　　2.5 構造出錯實例Tx

　　以Ut= x4+x3+1為例，對應尾部第1位處出了傳送錯，Ut加上x6后有U=x6+x4+x3+1，計算得Ec=U×G= （1110，1111，0101，1010，0000，01），整個錯誤序列的長度為22位。該Ec確定頭部出第1個傳送錯的位置是6，假定為漏刪填充位錯，則在尾部應取誤刪信息位錯。假定在頭部出現的是Tx送100000，在第6位處Rx收到的是1，出了第1個bit錯，第7位Rx得到填充位1而未刪去，Tx第7位可由Ec及Rx求得為0，然后逐位反推，得到Tx發生漏檢錯的實例，如圖3所示。

　　圖3 構造的會出漏檢錯的Tx實例

　　這個例子中Tx序列的長度為27 bit。此種長度的Tx可以有227種，每一種都可能出錯，但重構出的這一種在特定位發生2個bit錯時會漏檢。這個Tx在別的位置發生bit錯時，將可以檢出錯，因此它是一個可能被漏檢的可疑實例。Tx頭部共有4種可能：Tx=10000（0），10000（1），01111（1），01111（0）。（括號中的位在傳送中出了錯）。因此這幾種可疑實例占可能Tx的2-25。可疑Tx在64 bit的數據域中會有64-27+1=38種位置。對頭部Tx=100000和100001，其高4位可以與CAN的DLC重合，對Tx=011111和 011110，其最高位可和DLC0重合，因此此種Tx實例在8字節數據域的幀中出現的可能數目是39種。于是這一種漏檢實例有概率 39×2-25=1.16×10-6。當誤碼率為0.02時，64 bit內出2個bit錯的概率是（1-0.02）62×0.022=1.14×10-4，由這一個實例引起的CAN錯幀漏檢率就是1.32×10-10，已經大于Bosch的指標。考慮U中可增加的xk中k可由6一直到43，各種xk項有237=1.37×1011種組合，需要對每一種U進行計算，雖然它們的漏檢實例概率不同，其增量還是很大的。還要考慮不同Ut的貢獻，可見CAN錯幀漏檢率是非常大的。

　　2.6 計算結果

　　根據上述分析編制了在MATLAB中運行的程序pcan.m，在MATLAB中設置format long e格式，運行pcan（ber）即可得到不同誤碼率ber時的結果，如表2所列。

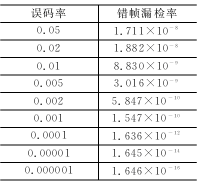
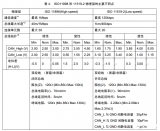
　　表2 典型的CAN漏檢錯幀概率

　　表中ber=0.02的錯幀漏檢率為1.882×10-8，而參考文獻在同樣誤碼率下給出的漏檢率是：低速系統4.7×10-14和高速系統 8.5×10-14。可見差別極大。對500 kbps的系統，假定總線利用率為40%，幀長為135 bit，那么按這個結果，CAN系統將在9.96小時出1個漏檢錯幀。

　　3 改善錯幀漏檢率的方法

　　在本文的分析中可以見到，由于填充位規則需要收發同步執行，不同步時會極大干擾CRC校驗，例如CRC校驗本來可以將所有奇數個錯檢測出的，小于5位的多 bit錯是可以檢測出的，但只要有了成對的填充位錯位，增加的奇數個錯也可以是漏檢的，增加的多bit錯也可以是漏檢的，如圖4所示。

　　圖4 有多位錯的例子

　　漏檢錯的根源是CAN的CRC在執行填充位規則前生成，最根本的解決辦法是像參考文獻［3］指出的那樣，要把CRC校驗放在執行填充位規則之后。但是這樣作就會根本修改CAN協議，在已經大量應用的情況下如何作到的改進前后的兼容性是個艱難的課題。作為局部的改正，參考文獻建議加附加的檢驗。在數據域添加一個新的不同的CRC檢驗時，根據本文的分析方法，當誤差多項式Ec是這個新CRC和CAN的CRC的公倍數時，仍然可以構造出漏檢的實例，并計算出新條件下的漏檢錯幀概率。例如采用8位的DARC?8生成多項式x8+x5+x4+x3+1，它不含x+1因子，所以與CAN生成多項式的最小公倍數構成的漏錯多項式Ec將有24階，此時如2.5節所分析的那樣，總幀數將增大28倍，而漏檢幀數不變，漏檢率就減少28。但是這種方法的缺點是不能實現自動報錯，無法使節點間取得數據的一致性：有局部錯的節點在添加上述措施后在收完幀后才能發現錯，已無法要其他節點也丟棄該幀并要求自動重發。

　　本文建議采用7b/8b的編碼辦法，犧牲一些帶寬，換取錯幀漏檢的避免。具體做法是在8b代碼中選取不會發生填充位條件的部分，供原來7b編碼使用。

　　其他的編碼辦法也是可行的，類似7b/8b的還有6b/7b、5b/6b、4b/5b，它們的區別是軟件實現時的復雜程度以及開銷占用數據域的多少，當用7b/8b時CAN可以每幀送7字節數據，而用4b/5b時每幀只能送6字節數據。

　　在附加數據域的軟件補丁后，若發生在ID域和CRC域的填充位規則只有單邊執行情況時，夾在它們中間的控制域就會左移或右移，幀長就會變大或變小。幀長的單位是1字節，它會使CRC域移入EOF域，CRC最多連續5位相同，就破壞了EOF的格式，或者EOF域移入CRC域，EOF的連續8位破壞了CRC的填充格式，所以此時單邊執行填充位規則的錯的后果是能被發現的。也就是說加軟件補丁后不再有錯幀漏檢可能。

　　如果可疑Tx只發生在ID域，由于Tx有一個最短長度，相應于Ec，t= x3+x+1，這個長度是3+15+6=24位，所以對CAN2.0B的29位ID可能會出錯，那么產生的后果就是接收節點收到的ID有錯，這是一種假冒錯（Masquerade）。在參考文獻中提到了CAN防止假冒錯的方法，實際上將ID分為二部分，一部分是一個附加的CRC，只要這個CRC生成多項式與CAN的不同，就不會產生假冒ID通過接收濾的可能。

　　4 小結

　　CAN的錯幀漏檢率對應用的可靠性有非常大的影響，本文發現了可能出錯漏檢的可疑幀重構的方法，從而求出的錯幀漏檢率高于Bosch提供的數據幾個數量級。對于已經在應用的大量可靠性要求高的系統，迫且需要應對的方案，2007年CAN芯片1年的出貨量為6億，可見影響之廣。本文提出了對數據添加 7b/8b編碼/譯碼的中間軟件補丁的方法。這種方法在犧牲部分帶寬，增加一些個復雜性的付出后，根本上解決了填充規則對CRC檢驗的干擾，使CAN的錯幀漏檢率回到與一般通信協議中CRC檢驗同等的水平。數據域犧牲的帶寬為8 bit，相對可能出現16 bit填充位而言，這算不了什么，而且減少了送達時間的抖動，可說是有好處的。不利之處是編碼/譯碼需要的時間與空間。

　　這個方法也可以在將來加入到芯片中去，利用CAN的保留位，識別有無7b/8b編碼/譯碼功能，從而實現與原有CAN2.0的兼容。有7b/8b編碼/譯碼功能時，需要的7b/8b編碼/譯碼、字長圓整以及幀長修正均可由硬件自動完成。