人工神經網絡(ANN)是一種從信息處理角度對人腦神經元網絡進行抽象從而建立的某種簡單模型,按不同的連接方式組成不同的網絡。其在語音識別、計算機視覺和文本處理等方面取得的突破性成果。
神經元
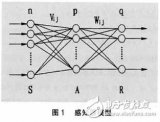
在神經網絡中,神經元是計算的基本單元,也被稱為節點或單元。它接受其他節點或外部的輸入,在計算后產生輸出。每兩個節點間的連接都代表一個對于通過該連接信號的加權值,稱之為權重(w)。該節點將一個函數f(定義如下)作用于輸入的加權和,如下圖所示
上述網絡采用數值輸入X1和X2、與輸入相關聯的權重w1和w2以及輸入權重b(稱為偏置)。稍后我們會介紹更多關于偏置的細節。
神經元輸出Y的計算上圖所示。函數f是非線性的,稱為激活函數。它的作用是將非線性引入到神經元的輸出中,以此達到神經元學習非線性表示的目的,滿足實際環境的數據要求。
每個激活函數都取一個數并對它進行特定的運算。在實際應用中我們可能會遇到下面幾種激活函數:
Sigmoid函數:σ(x)=1/(1+exp(?x))
tanh函數:tanh(x)=2σ(2x)?1
ReLU函數:f(x)=max(0,x)
下面是這幾個激活函數的圖像
偏差的重要性:如果沒有偏置的話,我們所有的分割線都是經過原點的,但是現實問題并不會那么如我們所愿。都是能夠是經過原點線性可分的。
前饋神經網絡
前饋神經網絡是第一個也是最簡單的人工神經網絡,各神經元從輸入層開始,接收前一級輸入,并輸出到下一級,直至輸出層。整個網絡中無反饋,可用一個有向無環圖表示。
前饋神經網絡結構如下圖所示
前饋神經網絡由三種節點組成:
1.輸入節點-輸入階段將來自外部的信息提供給網絡,統稱為“輸入層”。任何輸入節點都不執行計算,它們只是將信息傳遞給隱含階段。
2.隱含節點-隱含節點與外界沒有直接聯系(因此名稱為“隱含”)。他們執行計算并將信息從輸入節點傳輸到輸出節點。隱藏節點的集合形成“隱藏層”。雖然前饋網絡只有一個輸入層和一個輸出層,但它可以沒有或有多個隱藏層。
3.輸出節點-輸出節點統稱為“輸出層”,負責計算并將信息從網絡傳輸到外部世界。
前饋網絡的兩個例子如下:
1.單層感知器-這是最簡單的前饋神經網絡,不包含任何隱藏層。
2.多層感知器-多層感知器具有一個或多個隱藏層。我們只討論下面的多層感知器,因為它們比實際應用中的單層感知器更常用。
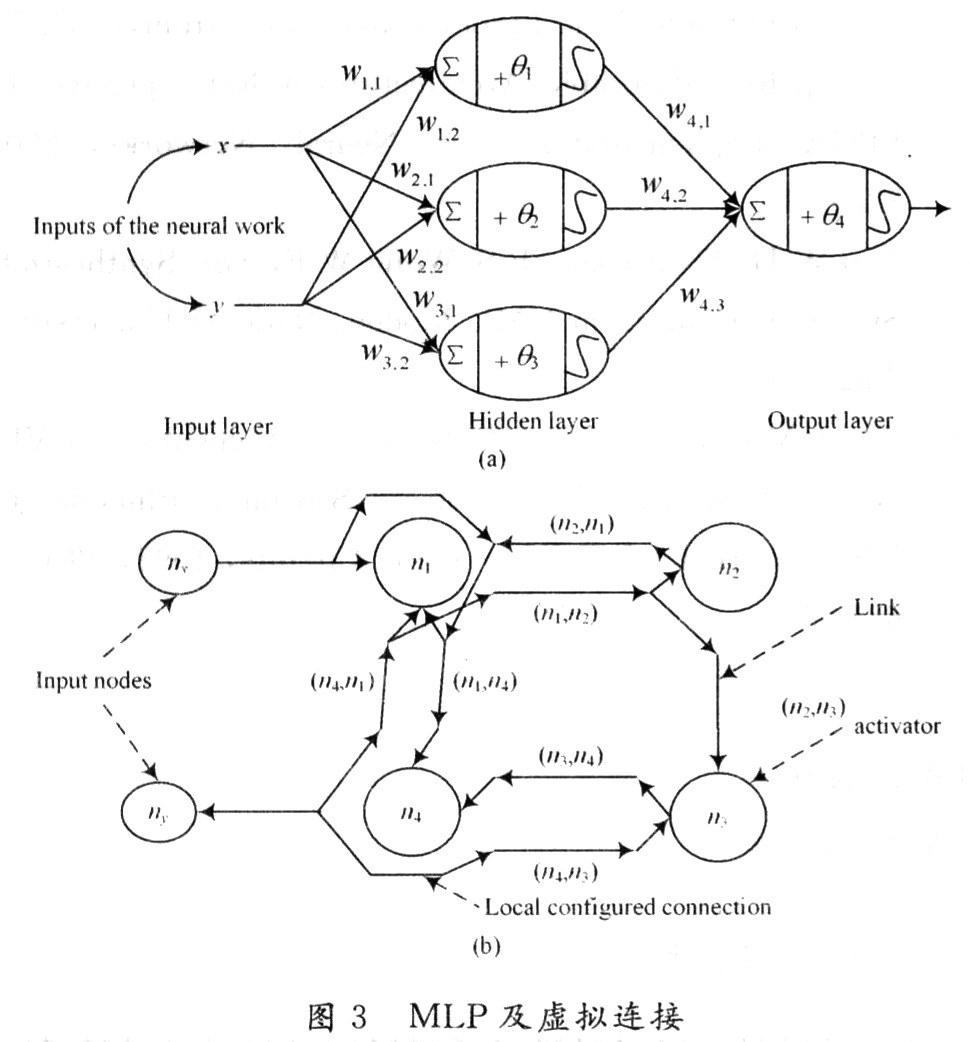
多層感知器
多層感知器(MLP)包含一個或多個隱藏層(除了一個輸入層和一個輸出層)。單層感知器只能學習線性函數,而多層感知器也可以學習非線性函數。
下圖顯示了具有單個隱藏層的多層感知器。需要注意的是,所有連接都有與之相關的權重,但圖中只顯示了三個權重(w0,w1,w2)。
輸入層:輸入層有三個節點。偏置節點的值為1,其他兩個節點將X1和X2作為外部輸入(數字值取決于輸入數據集)。
如上所述,在輸入層中不執行計算,所以來自輸入層中的節點的輸出分別是1,X1和X2,這些輸入被饋送到隱藏層中。
隱藏層:隱藏層也有三個節點,其偏置節點的輸出為1,隱藏層中另外兩個節點的輸出取決于輸入層(1,X1,X2)的輸出以及與其相關的權重。
下圖顯示了其中一個隱藏節點的輸出計算。同樣,可以計算其他隱藏節點的輸出。然后,這些輸出被反饋到輸出層中的節點。
輸出層:輸出層有兩個節點,它們從隱藏層獲取輸入,并執行與隱藏節點相似的計算。計算結果(Y1和Y2)將成為多層感知器的輸出。
給定一組特征X=(x1,x2,。。。)和一個目標y,多層感知器可以學習特征和目標之間的關系,無論是分類還是回歸。
我們舉個例子來更好地理解多層感知器。假設我們有以下的學生標記數據集:
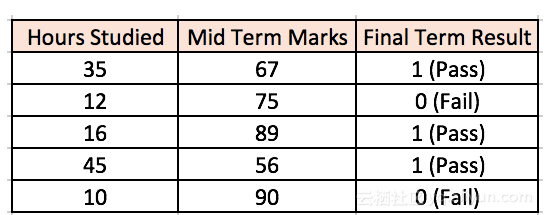
兩個輸入欄顯示學生學習的小時數和學生獲得的期中分數。最終結果欄可以有兩個值1或0,表示學生是否通過了期末測試。例如,我們可以看到,如果學生學習了35個小時,并在期中獲得了67分,他最終通過了期末測試。
現在假設我們想預測一個學習25小時,期中70分的學生是否能通過期末測試。

這是一個二元分類問題,其中多層感知器可以從給定的例子(訓練數據)中學習,并給出一個新的數據點的預測。我們將在下面看到多層感知器如何學習這種關系。
訓練我們的多層感知器
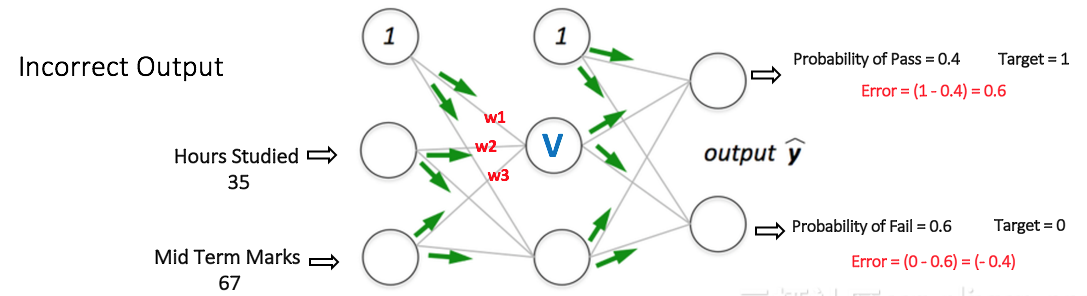
下圖所示的多層感知器在輸入層(除了偏置節點之外)有兩個節點,它們采用輸入“小時分析”和“期中標記”。它也有一個帶有兩個節點(除了偏置節點)的隱藏層。輸出層也有兩個節點-上層節點輸出“通過”的概率,而下層節點輸出“失敗”的概率。
在分類任務中,我們通常使用Softmax函數作為多層感知器的輸出層中的激活函數,以確保輸出是確實存在的,并且它們概率相加為1。Softmax函數采用任意實值向量,并且將其化為一個在0和1之間的矢量,其總和為1。所以,在這種情況下
P(合格)+P(不合格)=1
第1步:向前傳播
網絡中的所有權重都是隨機分配的。讓我們考慮圖中標記為V的隱藏層節點。假設從輸入到該節點的連接的權重是w1,w2和w3(如圖所示)。
然后網絡將第一個訓練樣例作為輸入(我們知道對于輸入35和67,通過的概率是1)。
輸入到網絡=[35,67]
來自網絡的期望輸出(目標)=[1,0]
那么考慮節點的輸出V可以計算如下(f是一個激活函數,如Sigmoid函數):
V=f(1*w1+35*w2+67*w3)
同樣,也計算隱藏層中另一個節點的輸出。隱藏層中兩個節點的輸出作為輸出層中兩個節點的輸入。這使我們能夠計算輸出層中兩個節點的輸出概率。
假設輸出層兩個節點的輸出概率分別為0.4和0.6(因為權重是隨機分配的,所以輸出也是隨機的)。我們可以看到,計算的概率(0.4和0.6)與期望的概率(分別為1和0)相差很遠,因此圖中的網絡被認為有“不正確的輸出”。
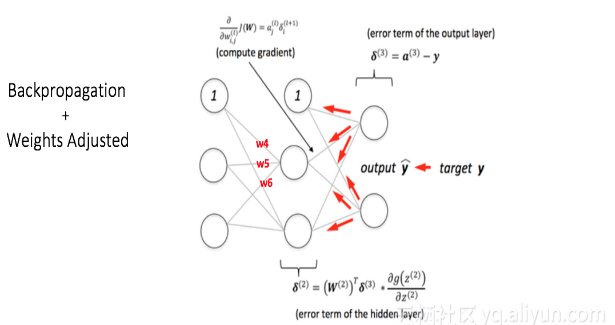
第2步:向后傳播和權重更新
我們計算輸出節點處的總誤差,并使用反向傳播將這些誤差返回網絡以計算梯度。然后,我們使用一種優化方法諸如梯度下降,以減小輸出層誤差在網絡中的權重。這將在下面的圖中顯示。
假設與所考慮的節點相關的新權重是w4,w5和w6(在反向傳播和調整權重之后)。
如果我們現在再次向網絡輸入相同的示例,則網絡應該比以前執行得更好,因為權重現在已經被調整到最小化誤差。如圖所示,與之前的[0.6,-0.4]相比,輸出節點的誤差現在降低到[0.2,-0.2]。這意味著我們的神經網絡已經學會了正確的分類我們的第一個訓練樣例。
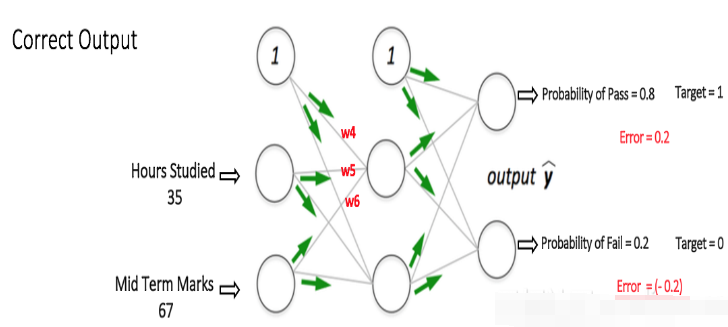
我們在數據集中重復這個過程和所有其他的訓練樣例。那么,神經網絡將完全學會這些例子。
如果我們現在要預測一個學習25小時,期中有70分的學生是否能通過期末測試,我們就要經過前向傳播步驟,找到通過和失敗的概率。
多層感知器的三維可視化
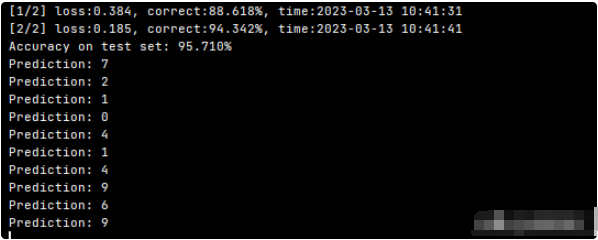
AdamHarley創建了一個已經在手寫數字的MNIST數據庫上訓練(使用反向傳播)的多層感知器的三維可視化。
網絡將784個數字像素值作為來自手寫數字(其在輸入層中具有對應于像素的784個節點)的28×28圖像的輸入。網絡在第一個隱藏層有300個節點,第二個隱藏層有100個節點,輸出層有10個節點(對應于10個數字)。
雖然這里描述的網絡比前一節討論的要大得多(使用更多的隱藏層和節點),但正向傳播步驟和反向傳播步驟中的所有計算都是按照相同的方式(在每個節點處)進行的之前。
較亮的顏色表示比其他更高的輸出值的節點。在輸入層中,亮節點是那些接收較高像素值作為輸入的節點。在輸出層中,唯一亮節點對應于數字5(它的輸出概率為1,比輸出概率為0的其他九個節點高)。這表明MLP已經正確分類輸入的數字。我強烈推薦使用這個可視化例子來觀察不同層次的節點之間的連接。
責任編輯人:CC
 電子發燒友App
電子發燒友App
























評論