本質上，深度學習是一個新興的時髦名稱，衍生于一個已經存在了相當長一段時間的主題——神經網絡。 ?

從20世紀40年代開始，深度學習發展迅速，直到現在。該領域取得了巨大的成功，深度學習廣泛運用于智能手機、汽車和許多其他設備。

那么，什么是神經網絡，它可以做什么？

現在，一起來關注計算機科學的經典方法：

程序員設計一種算法，它對于給定的輸入數據，生成輸出數據。

程序員們準確地設計函數f（x）的所有邏輯：

y = f(x)

其中x和y分別是輸入數據和輸出數據

但是，有時設計 f(x) 可能并不那么容易。例如，假設x是面部圖像，y是通信員的名字。對于大腦來說，這項任務非常容易，而計算機算法卻難以完成！

這就是深度學習和神經網絡大顯神通的地方。

基本原則是：放棄 f() 算法，試著模仿大腦。

那么，大腦是如何表現的？

大腦使用幾個無限對 (x，y) 樣本（訓練集）不斷訓練，在這個過程中，f(x) 函數會自動形成。它不是由任何人設計的，而是從無休止的試錯法提煉機制中形成的。

想想一個孩子每天看著周圍熟悉的人：數十億個快照，取自不同的位置、視角、光線條件，每次識別都要進行關聯，每次都要修正和銳化自然神經網絡。

人工神經網絡是由大腦中的神經元和突觸組成的自然神經網絡模型。

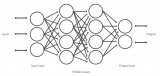
典型的神經網絡結構

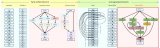
為了保持簡單，并且利用當今機器的數學和計算能力，可以將神經網絡設計為一組層，每層包含節點（大腦神經元的人工對應物），其中層中的每個節點連接到下一層中的節點。

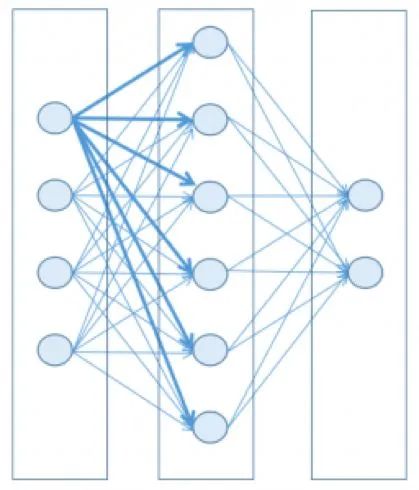
每個節點都有一個狀態，通過浮點數表示，其取值范圍通常介于0到1。該狀態接近其最小值時，該節點被認為是非活動的（關閉），而它接近最大值時，該節點被認為是活動的（打開）。可以把它想象成一個燈泡；不嚴格依賴于二進制狀態，但位于取值范圍內的某個中間值。

每個連接都有一個權重，因此前一層中的活動節點或多或少地會影響到下一層中節點的活動（興奮性連結），而非活動節點不會產生任何影響。

連接的權重也可以是負的，這意味著前一層中的節點（或多或少地）對下一層中的節點的不活動性（抑制性連結）產生影響。

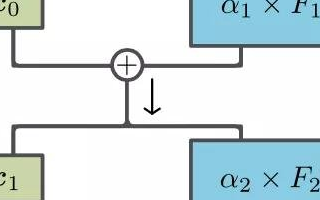
簡單來說，現在假設一個網絡的子集，其中前一層中的三個節點與下一層中的節點相連結。簡而言之，假設前一層中的前兩個節點處于其最大激活值（1），而第三個節點處于其最小值（0）。

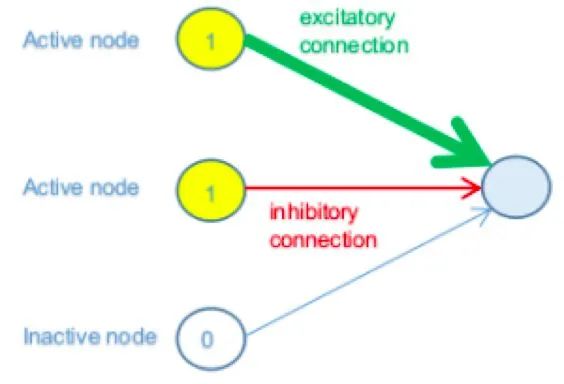
在上圖中，前一層中的前兩個節點是活動的（開），因此，它們對下一層中節點的狀態有所貢獻，而第三個節點是非活動的（關），因此它不會以任何方式產生影響（獨立于其連結權重）。

第一個節點具有強（厚）正（綠色）連接權重，這意味著它對激活的貢獻很大。第二個具有弱（薄）負（紅色）連接權重；因此，它有助于抑制連接節點。

最后，得到了來自前一層的傳入連接節點的所有貢獻值的加權和。

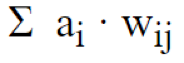
其中i是節點 i 的激活狀態，w ij是連接節點 i 和節點 j 的連接權重。

那么，給定加權和，如何判斷下一層中的節點是否會被激活？規則真的像“總和為正即被激活，結果為負則不會”？有可能，但一般來說，這取決于你為這個節點選擇哪個激活函數及閾值）。

想一想。這個最終數字可以是實數范圍內的任何數字，我們需要使用它來設置更有限范圍內的節點狀態（假設從0到1）。然后將第一個范圍映射到第二個范圍，以便將任意（負數或正數）數字壓縮到0到1的范圍內。

sigmoid 函數是執行此任務的一個常見激活函數。

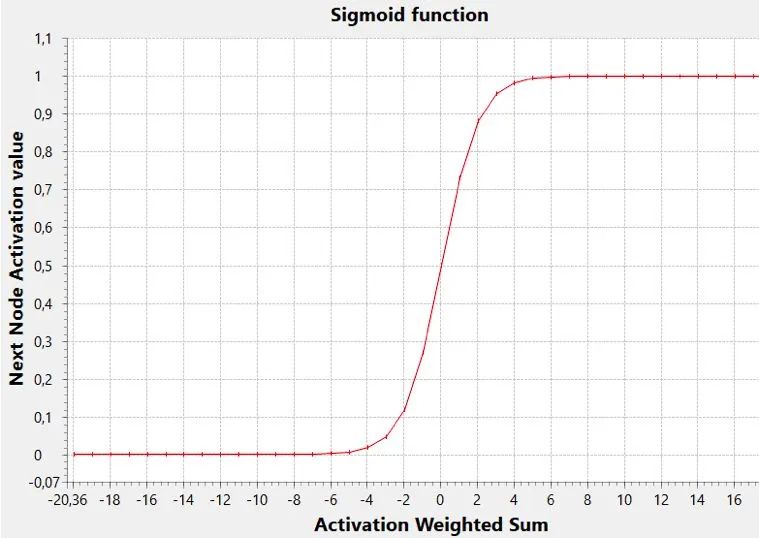
在該圖中，閾值（y 值達到范圍中間的 x 值，即0.5）為零，但一般來講，它可以是任何值（負數或正數，其變化影響sigmoid向左或向右移動）。

低閾值允許使用較低的加權和激活節點，而高閾值將僅使用該和的高值確定激活。

該閾值可以通過考慮前一層中的附加虛節點來實現，其激活值恒定為 1。在這種情況下，該虛節點的連接權重可以用作閾值，并且上文提到的和公式可以被認為包括閾值本身。

最終，網絡的狀態由其所有權重的一組值來表示（從廣義上講，包括閾值）。

給定狀態或一組權重值可能會產生不良結果或大錯誤，而另一個狀態可能會產生良好結果，換句話說，就是小錯誤。

因此，在N維狀態空間中移動會造成小錯誤或大錯誤。損失函數能將權重域映射到錯誤值的函數。在n+1空間里，人們的大腦很難想象這樣的函數。但是，對于N = 2是個特殊情況。

訓練神經網絡包括找到最小的損失函數。為什么是最佳最小值而不是全局最小值？其實是因為這個函數通常是不可微分的，所以只能借助一些 梯度下降技術在權重域中游蕩，并避免以下情況：

做出太大的改變，可能你還沒意識到就錯過最佳最小值

做出太小的改變，你可能會卡在一個不太好的局部最小值

不容易，對吧？這就是深度學習的主要問題，也解釋了為什么訓練階段可能要花數小時、數天甚至數周。

這就是為什么硬件對于此任務至關重要，同時也解釋了為什么經常需要暫停，考慮不同的方法和配置參數來重新開始。

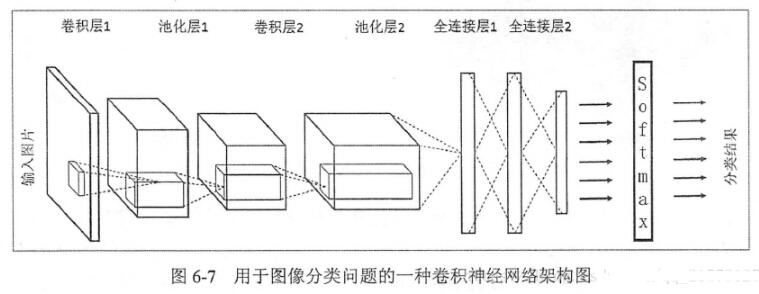
現在回到網絡的一般結構，這是一堆層。第一層是輸入數據 (x)，而最后一層是輸出數據 (y)。

中間的層可以是零個、一個或多個。它們被稱為隱藏層，深度學習中的“深度”一詞恰好指的是網絡可以有許多隱藏層，因此可能在訓練期間找到更多關聯輸入和輸出的特征。

提示：在20世紀90年代，你會聽說過多層網絡而不是深度網絡，但這是一回事。現在，越來越清楚的是，篩選層離輸入層越遠（深），就能越好地捕捉抽象特征。

學習過程

在學習過程開始時，權重是隨機設置的，因此第一層中的給定輸入集將傳送并生成隨機（計算）輸出數據。將實際輸出數據與期望輸出數據進行比較；其差異就是網絡誤差（損失函數）的度量。

然后，此錯誤用于調整生成它的連接權重，此過程從輸出層開始，逐步向后移動到第一層。

調整的量可以很小，也可以很大，并且通常在稱為學習率的因素中定義。

這種算法稱為反向傳播，并在Rumelhart，Hinton和Williams研究之后，于1986年開始流行。

記住這個名字：杰弗里·辛頓 (Geoffrey Hinton)，他被譽為“深度學習的教父”，是一位孜孜不倦的科學家，為他人指引前進方向。例如，他現在正在研究一種名為膠囊神經網絡 (Capsule Neural Networks) 的新范式，聽起來像是該領域的另一場偉大革命！

反向傳播旨在通過對訓練每次集中迭代的權重進行適當的校正，來逐漸減少網絡的整體誤差。另外，減少誤差這個步驟很困難，因為不能保證權重調整總是朝著正確的方向進行最小化。

簡而言之，你戴著眼罩走來走去時，在一個n維曲面上找到一個最小值：你可以找到一個局部最小值，但永遠不知道是否可以找到更小的。

如果學習率太低，則該過程可能過于緩慢，并且網絡也可能停滯在局部極小值。另一方面，較高的學習率可能導致跳過全局最小值并使算法發散。

事實上，訓練階段的問題在于，錯誤只多不少！

現狀

為什么這個領域現在取得如此巨大的成功？

主要是因為以下兩個原因：

訓練所需的大量數據（來自智能手機、設備、物聯網傳感器和互聯網）的可用性

現代計算機的計算能力可以大大縮短訓練階段（訓練階段只有幾周甚至幾天的情況很常見）

想了解更多？這里有幾本好書推薦：

亞當?吉布森（Adam Gibson）和 喬希·帕特森（Josh Patterson）所著的《深度學習》，O’Reilly媒體出版社。

莫希特·賽瓦克（Mohit Sewark）、默罕默德·禮薩·卡里姆（Md Rezaul Karim）和普拉蒂普·普賈里（Pradeep Pujari）所著的《實用卷積神經網絡》， Packt出版社。

審核編輯 ：李倩

?