問題來源

最近讀到一篇模型蒸餾的文章 [1]，其中在設計軟標簽的損失函數(shù)時使用了一種特殊的 softmax： ?

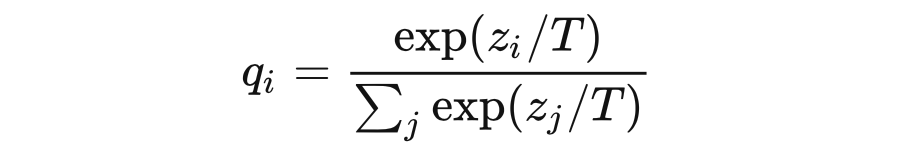
文章中只是簡單的提了一下，其中 T 是 softmax 函數(shù)的溫度超參數(shù)，而沒有做過多解釋。這說明這種用法并非其首創(chuàng)，應該是流傳已久。經(jīng)過一番調研和學習，發(fā)現(xiàn)知乎上最高贊的文章《深度學習中的 temperature parameter 是什么》[13] 對超參數(shù) T 的講解具有很強的誤導性，所以在此重新寫一篇文章為其正名。 ? 本文的標題有兩個雙關。一個是知識蒸餾的方法用于深度學習，同時也需要深入學習；另一個則是本文的核心：蒸餾中如何合理運用溫度，讓隱藏的知識更好地揮發(fā)和凝結。下面我將詳細講解以上 softmax 公式中溫度系數(shù)的由來以及它起到的作用。 ? ?

蒸餾模型

模型蒸餾或知識蒸餾，最早在 2006 年由 Buciluǎ 在文章 Model Compression?[14]?中提出（很多博主把人名都寫錯了。其后，Hinton 進行了歸納和發(fā)展，并在 2015 年發(fā)表了經(jīng)典之作 Distilling the Knowledge in a Neural Network [15]。正是在這篇文章 [2] 中，Hinton 首次提出了 Softmax with Temperature 的方法。 ? 先簡要概括一下模型蒸餾在做什么。出于計算資源的限制或效率的要求，深度學習模型在部署推斷時往往需要進行壓縮，模型蒸餾是其中一種常見方法。將原始數(shù)據(jù)集上訓練的重量級（cumbersome）模型作為教師，讓一個相對更輕量的模型作為學生。 ? 對于相同的輸入，讓學生輸出的概率分布盡可能的逼近教師輸出的分布，則大模型的知識就通過這種監(jiān)督訓練的方式「蒸餾」到了小模型里。小模型的準確率往往下降很小，卻能大幅度減少參數(shù)量，從而降低推斷時對 CPU、內(nèi)存、能耗等資源的需求。 ? 對于傳統(tǒng)的監(jiān)督訓練，損失函數(shù)可以寫為 KL-散度 ，表示用分布 擬合分布 帶來的誤差。其中 是輸出的真實分布，我們的數(shù)據(jù)集的標簽 就從這個分布中采樣而來，對于一個 分類問題， 常常會表示為 one-hot 向量，包含 1? 個 1 和 個 0。對于模型蒸餾，損失函數(shù)可以表示為 ，表示用學生模型的輸出 來擬合教師模型的輸出 。 ? 我們知道模型在訓練收斂后，往往通過 softmax 的輸出不會是完全符合 one-hot 向量那種極端分布的，而是在各個類別上均有概率，推斷時通過 argmax 取得概率最大的類別。Hinton 的文章就指出，教師模型中在這些負類別（非正確類別）上輸出的概率分布包含了一定的隱藏信息。比如 MNIST 手寫數(shù)字識別，標簽為 7 的樣本在輸出時，類別 7 的概率雖然最大，但和類別 1 的概率更加接近，這就說明 1 和 7 很像，這是模型已經(jīng)學到的隱藏的知識。 ? 我們在使用 softmax 的時候往往會將一個差別不大的輸出變成很極端的分布，用一個三分類模型的輸出舉例： ?

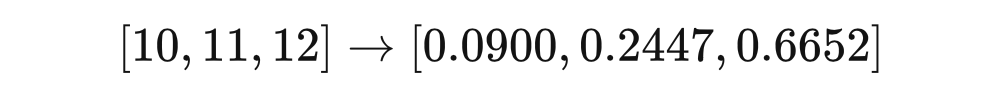
可以看到原本的分布很接近均勻分布，但經(jīng)過 softmax，不同類別的概率相差很大。這就導致類別間的隱藏的相關性信息不再那么明顯，有誰知道 0.09 和 0.24 對應的類別很像呢？為了解決這個問題，我們就引入了溫度系數(shù)。 ? ?

溫度系數(shù)

我們看看對于隨機生成的相同的模型輸出，經(jīng)過不同的函數(shù)處理，分布會如何變化： ?

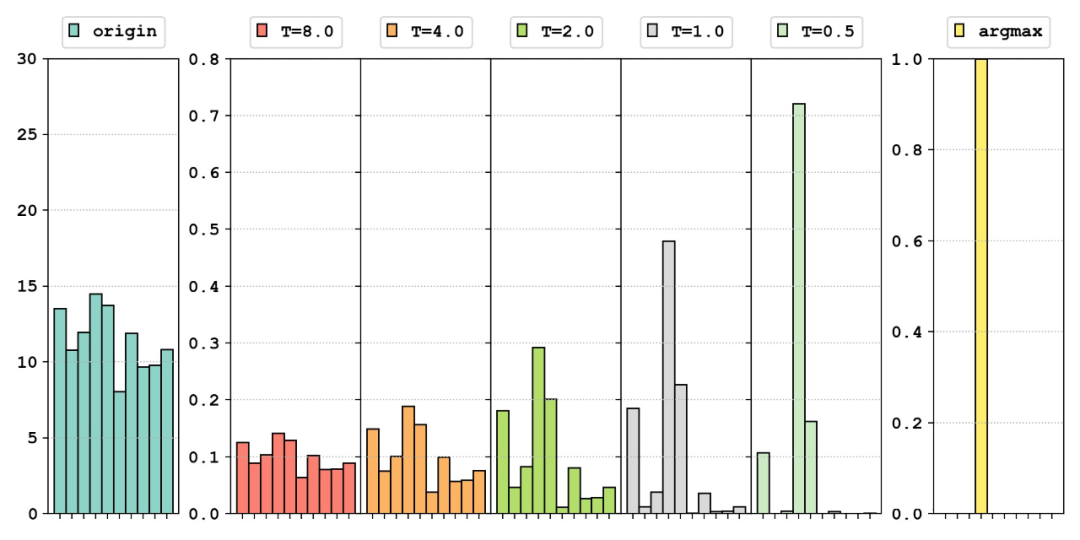
最左邊是我們隨機生成的分布來模擬模型的輸出：。中間五幅圖是使用 softmax 得到的結果；其中溫度系數(shù) 時相當于原始的 softmax；右側對比了 argmax 得到的結果。可以看出，從左到右，這些輸出結果逐漸從均勻分布向尖銳分布過渡，其中保留的除正確類別以外的信息越來越少。下圖 [3] 更加直觀地展示了不同的溫度系數(shù) 對輸出分布的影響。 ?

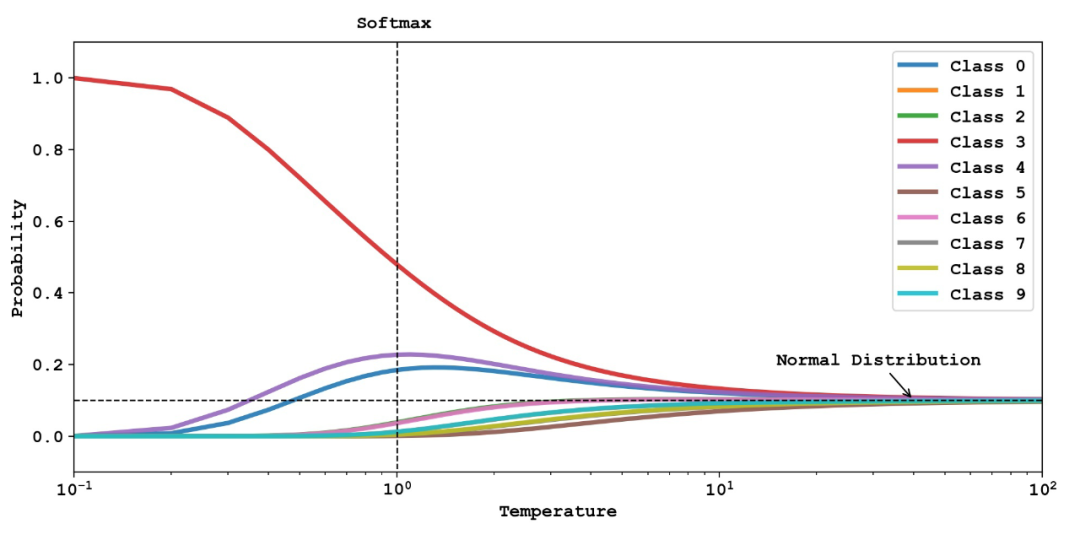
靈感來源：https://www.youtube.com/watch?v=tOItokBZSfU

不同的曲線代表不同類別上的概率輸出，同樣 時代表傳統(tǒng)的 softmax，在 時，分布逐漸極端化，最終等價于 argmax，在 時，分布逐漸趨于均勻分布，10 個類別的概率都趨近于1/10。 ? 這兩幅畫很好的說明了 softmax 的本質。相對于 argmax 這種直接取最大的「hardmax」，softmax 采用更溫和的方式，將正確類別的概率一定程度地突顯出來。而引入溫度系數(shù)的本質目的，就是讓 softmax 的 soft 程度變成可以調節(jié)的超參數(shù)。 ?

而至于這個系數(shù)為啥叫 Temperature，其實很有深意。我們知道這個場景最早用于模型蒸餾，一般來說蒸餾需要加熱，而加熱會導致熵增。我們發(fā)現(xiàn)，提高溫度系數(shù)會導致輸出分布的信息熵增大！[4] 而在 Hinton 的這篇論文里，為了充分利用教師模型負類別的 dark 信息，一般會選用一個較高的溫度系數(shù)，這也是本文標題叫做高溫蒸餾的原因。 ? 我們可以輕松地推導出 趨于無窮大時，分布將趨于均勻分布，此時信息熵趨于最大 ?

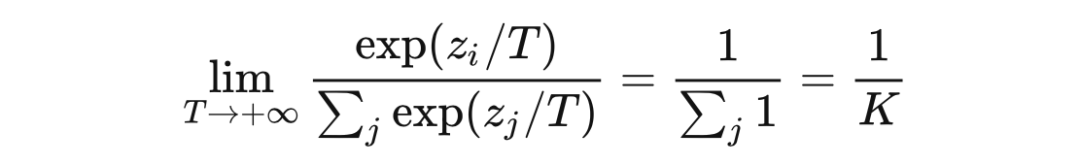
而當 趨于 0 時，正確類別的概率接近 1，softmax 的效果逼近 argmax ?

?

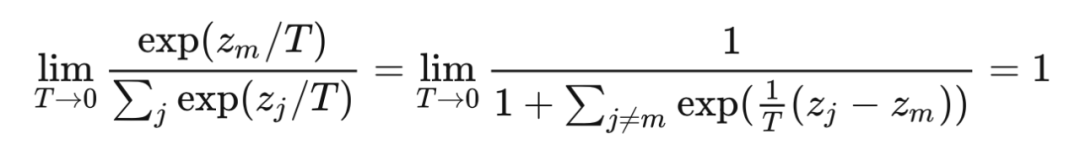
反對意見

在最高贊的那篇文章中提到：

如果我們在訓練時將t設置比較大，那么預測的概率分布會比較平滑，那么loss會很大

首先，如果原文考慮的問題中數(shù)據(jù)的標簽是 one-hot 向量而不是蒸餾這種軟標簽， 較大時 loss 確實會較大，因為輸出分布比較均勻，不能很好地凸顯正類別上的概率優(yōu)勢。但在蒸餾時并非如此，Hinton 給出的 Loss 函數(shù)如下圖 [5] 所示，分為兩項： ?

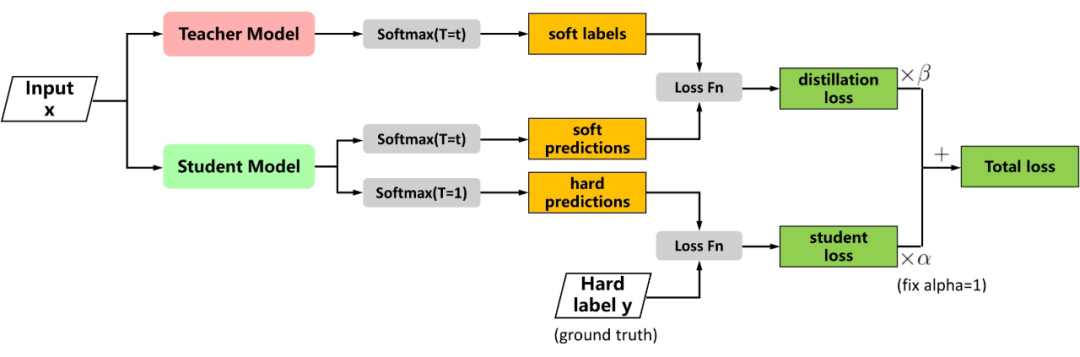
圖源：https://nni.readthedocs.io/en/stable/sharings/kd_example.html

第一項? 是教師模型與學生模型的輸出之間的交叉熵，第二項 是學生模型與真實標簽之間的交叉熵。傳統(tǒng)訓練模型時只有 項，所以 可以看做是引入的正則項。文中指出這個正則項使得學生模型能夠學到教師模型中的高度泛化的知識，從而需要更少的真實訓練樣本。 ? 文中的實驗只用了 3% 的訓練樣本，就達到了近似教師模型的準確率。我們可以看到這里的 項中，兩個模型都使用了同樣的、較大的溫度系數(shù) ，對輸出的作用是相同的，未必會使 loss 變大。 ?

……那么loss會很大，這樣可以避免我們陷入局部最優(yōu)解。

為什么 loss 大就可以避免陷入局部最優(yōu)呢？我猜作者想表達的是 loss 很大，從而隨機梯度下降的時候梯度很大，步長就會很大，從而更容易跳出局部最優(yōu)。該文章的評論區(qū)也有同樣的聲音，但可惜這并不正確。我們還以硬標簽 監(jiān)督訓練為例，使用交叉熵損失函數(shù)，設 softmax 的輸出為 ，我們可以推導 loss 對于模型輸出 的梯度： ?

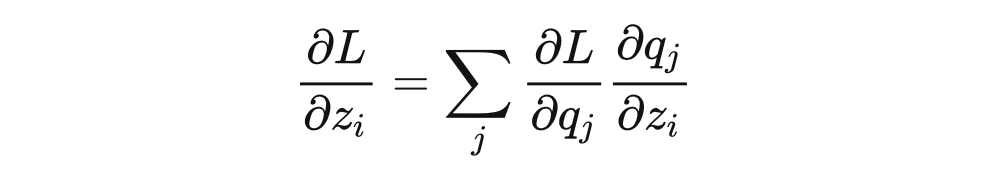
交叉熵的梯度 ?

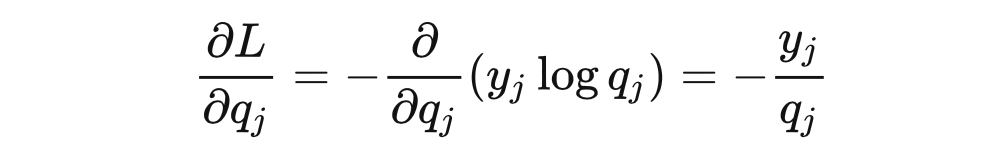
softmax 的梯度 ?

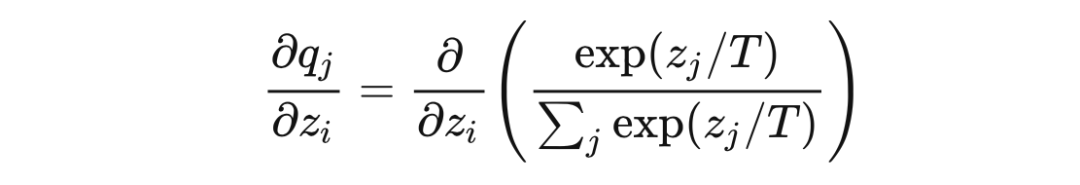
當 時 ?

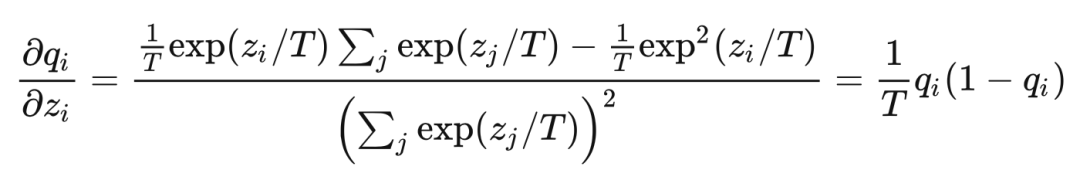
當 時 ?

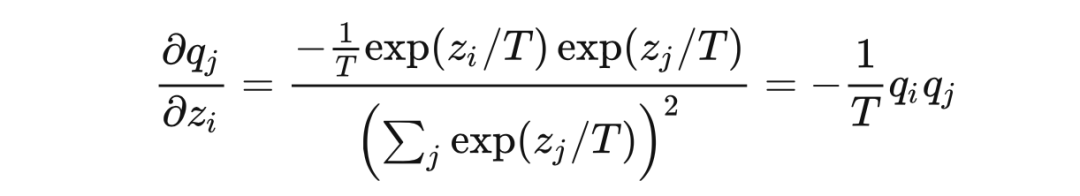
代入鏈式法則，最終的梯度為（推導參考了 [6][7]） ?

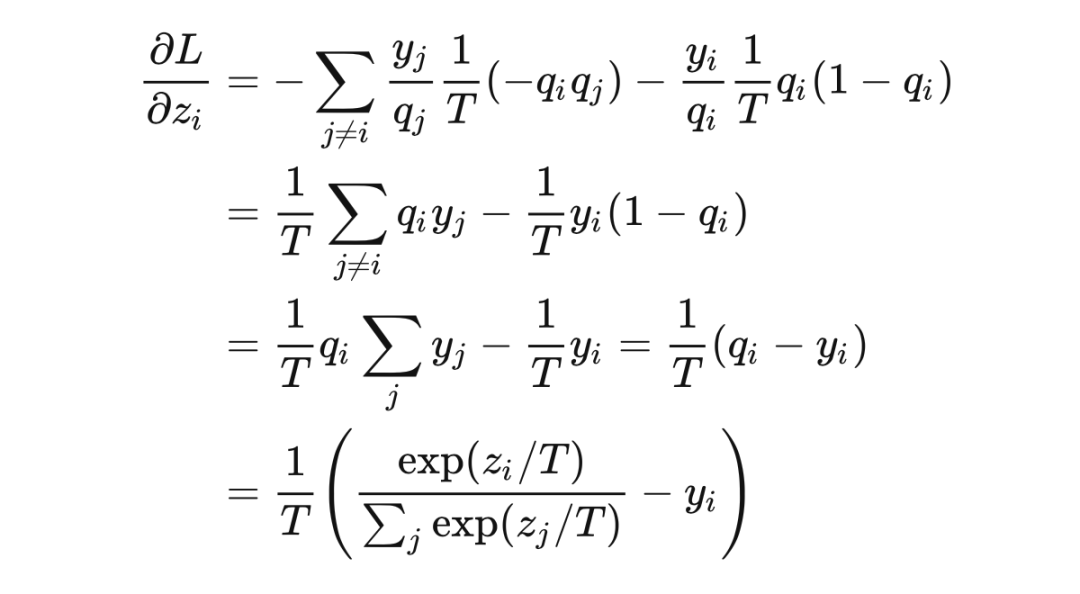
顯然標簽 與 softmax 的輸出 之差不總能增長 倍，大家可以自己舉一些反例，會發(fā)現(xiàn)大多數(shù)情況下，梯度都不是增大的。那么對于 Hinton 這篇論文，由于 loss 的數(shù)量級沒有變化，所以梯度實際是減小的，所以文章中特意強調了要將系數(shù) 設置大一些來補償，比如設置為 ，在這里給出的 Pytorch 實現(xiàn) [16] 中也是這么做的。 ? 文章中給出了一個高溫情況下的等價，在 時，利用等價無窮小或者是泰勒展開得到： ?

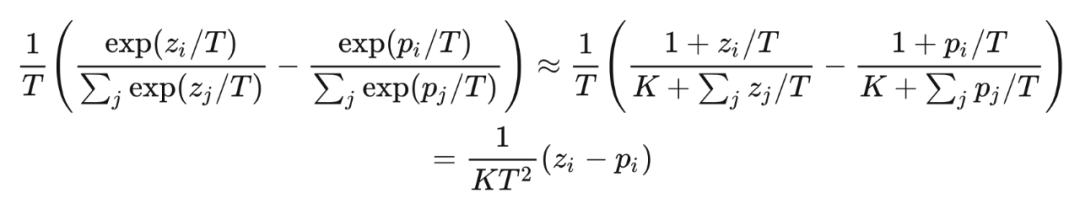
可以清晰的看出這里是 的關系。 ?

隨著訓練的進行，我們將 t 變小，也可以稱作降溫，類似于模擬退火算法，這也是為什么要把 t 稱作溫度參數(shù)的原因。變小模型才能收斂。

我不知道將這里的溫度系數(shù)類比模擬退火算法的溫度系數(shù)有什么依據(jù)（Quora 上有個類似的 [8]），但它們真的是不怎么像。同樣也未必是溫度系數(shù)變小模型才能收斂，需要分情況：如果是模型蒸餾， 項始終都使用較大的溫度；如果是使用真實標簽訓練，確實選取較小的溫度系數(shù)，更利于模型收斂。 ? 可以這樣理解，溫度系數(shù)較大時，模型需要訓練得到一個很陡峭的輸出，經(jīng)過 softmax 之后才能獲得一個相對陡峭的結果；溫度系數(shù)較小時，模型輸出稍微有點起伏，softmax 就很敏感地把分布變得尖銳，認為模型學到了知識。 ? 所以，使用一個固定的小于 1 的溫度系數(shù)是合理的，這也是那篇文章里提到的推薦系統(tǒng)所做的，它沒有降溫過程，直接設置了?T=0.05?。如果大家在哪篇文章中看到了降溫過程，還請在評論區(qū)指正。 ? ?

其他場景

? 這里我們天馬行空地設想一個場景：在一些序列生成任務中，比如 seq2seq 的機器翻譯模型，或者是驗證碼識別的 CTC 算法 [9] 中，輸出的每一個時間步都會有一個分布。最終的序列會使用 BeamSearch [10] 或者 Viterbi [11] 等算法搜索 Top-K 概率的序列。 ? 這類方法介于逐時間步 argmax 的完全貪心策略和全局動態(tài)規(guī)劃的優(yōu)化策略之間。雖然 BeamSearch 中我們不需要提前 softmax，但假如我們做了帶溫度系數(shù)的 softmax，就可以控制輸出分布的尖銳程度。對于這類逐步計算累積概率的算法，在每個時間步的概率分布較為均勻時就容易輸出不同的結果。所以在這類問題下，高溫可能導致輸出序列的多樣性。 ? 對于這類場景，我沒有進行嚴格證明也沒有很深的經(jīng)驗，只是一個猜想。這里有類似的說法 [12]，但都不能作為參考依據(jù)。大家感興趣的話可以將 softmax with temperature 引入 BeamSearch 看看會不會對輸出的豐富性造成影響。假如算法只依賴每個時間步的概率大小關系，那輸出就是確定的，說明我們猜想失敗。或者有相關經(jīng)驗的同學也可以在評論區(qū)給出參考文獻。 ? ?

后話

寫完這篇文章才發(fā)現(xiàn)，潘小小【經(jīng)典簡讀】知識蒸餾（Knowledge Distillation）經(jīng)典之作 [17] 一文中已有類似的探討。盡管如此，我相信這篇文章還是可以起到一定的科普作用，讓那些和我一樣對知識蒸餾不太了解的同學，從溫度系數(shù)這個關鍵詞入手，能夠快速得到想要的答案。 ? 讀完 Hinton 的文章，有兩個強烈的感受：一是感覺他太牛了，3 句話讓我讀了? 18 遍，全文很少用公式，基本沒有配圖，但把算法講得清清楚楚；二就是，他的寫作中長從句實在太多了，一句話 60 個單詞，讀起來很不友好。如果對這篇文章感興趣，也可以看上面潘小小的那篇解讀。文章最后講到了一種和 MOE 很像的分布式集成學習方法，在潘的文章中沒有介紹，由于這不是今天的主題，所以我也沒用筆墨，大家如果對這部分感興趣也可以來找我討論。 ? 說出來很難相信，我其實不是做 AI 方向的，我是做系統(tǒng)的，所以歡迎大家懟我（°ー°〃）。 ? ? ?

參考文獻

[1] Group knowledge transfer: Federated learning of large cnns at the edgehttps://proceedings.neurips.cc/paper/2020/file/a1d4c20b182ad7137ab3606f0e3fc8a4-Paper.pdf

[2]Distilling the Knowledge in a Neural Network?https://arxiv.org/abs/1503.02531

[3] PR-009: Distilling the Knowledge in a Neural Network (Slide: English, Speaking: Korean)?https://www.youtube.com/watch?v=tOItokBZSfU

[4] What is the role of temperature in Softmax?https://stats.stackexchange.com/questions/527080/what-is-the-role-of-temperature-in-softmax#answer-527082

[5] Knowledge Distillation on NNIhttps://nni.readthedocs.io/en/stable/sharings/kd_example.html

[6] softmax, CrossEntropyLoss 與梯度計算公式https://blog.csdn.net/jiongjiongai/article/details/88324000

[7] 關于Softmax的數(shù)值穩(wěn)定性和梯度反向傳播https://zhuanlan.zhihu.com/p/92714192

[8] What is the temperature parameter in deep learning?https://www.quora.com/What-is-the-temperature-parameter-in-deep-learning

[9] 詳解CTChttps://zhuanlan.zhihu.com/p/42719047

[10] 文本生成解碼之 Beam Searchhttps://zhuanlan.zhihu.com/p/43703136

[11] 如何通俗地講解 viterbi 算法？https://www.zhihu.com/question/20136144/answer/763021768

[12]What is Temperature in LSTM??https://www.quora.com/What-is-Temperature-in-LSTM

[13] https://zhuanlan.zhihu.com/p/132785733?

[14] https://dl.acm.org/doi/abs/10.1145/1150402.1150464?

[15] https://arxiv.org/abs/1503.02531?

[16]?https://nni.readthedocs.io/en/stable/sharings/kd_example.html?

[17] https://zhuanlan.zhihu.com/p/102038521

編輯：黃飛