目標檢測是計算機視覺領域的重要研究方向. 傳統的目標檢測方法在特征設計上花費了大量時間, 且手工設計的特征對于目標多樣性的問題并沒有好的魯棒性, 深度學習技術逐漸成為近年來計算機視覺領域的突破口. 為此, 對現有的基礎神經網絡進行研究, 采用經典卷積神經網絡VGGNet作為基礎網絡, 添加部分深層網絡, 結合SSD (single shot multibox detector)算法構建網絡框架. 針對模型訓練中出現的正負樣本不均衡問題, 根據困難樣本挖掘原理, 在原有的損失函數中引入調制因子, 將背景部分視為簡單樣本, 減小背景損失在置信損失中的占比, 使得模型收斂更快速, 模型訓練更充分, 從而提高復雜背景下的目標檢測精度. 同時, 通過構建特征金字塔和融合多層特征圖的方式, 實現對低層特征圖的語義信息融合增強, 以提高對小目標檢測的精度, 從而提高整體的檢測精度. 仿真實驗結果表明, 所提出的目標檢測算法(feature fusion based SSD, FF-SSD)在復雜背景下對各種目標均可取得較高的檢測精度.

關鍵詞

目標檢測????深度學習????SSD算法????復雜背景????困難樣本????特征融合? ?

?引言

復雜背景下的目標檢測是計算機視覺領域中一個十分重要的課題. 傳統的目標檢測方法面臨以下兩個問題: 一是基于滑動窗口的區域選擇策略容易產生窗口冗余; 二是手工設計的特征對于目標多樣性的變化并沒有好的魯棒性. 因此, 基于深度學習的目標檢測方法開始受到人們的廣泛關注. 深度學習方法能克服傳統人工選取特征的缺點, 自適應地學習表征目標的最佳特征, 且抗干擾性能優異, 可以有效提高目標識別的準確性和魯棒性[1].

在深度學習目標檢測模型中, 具有代表性的是Girshick等[2]提出的一系列目標檢測算法, 其開山之作是R-CNN (region-convolutional neural network). 針對R-CNN訓練時間過長的問題, Girshick[3]又提出了Fast R-CNN. 與R-CNN類似, Fast R-CNN依然采用selective search[4]生成候選區域, 但是, 與R-CNN提取出所有候選區域并使用SVM分類的方法不同, Fast R-CNN在整張圖片上使用CNN, 然后使用特征映射提取感興趣區域(region of interest, RoI); 同時, 利用反向傳播網絡進行分類和回歸. 該方法不僅檢測速度快, 而且具有RoI集中層和全連接層, 使得模型可求導, 更容易訓練. Ren等[5]又提出了Fast R-CNN的升級版本Faster R-CNN算法. Faster R-CNN是第一個真正意義上端到端的、準實時的深度學習目標檢測算法. Faster R-CNN最大的創新點在于設計了候選區域生成網絡(region proposal network, RPN), 并設計了anchor機制. 從R-CNN到Fast R-CNN再到Faster R-CNN, 候選區域生成、特征提取、候選目標確認以及邊界框坐標回歸被逐漸統一到同一個網絡框架中.

同樣是基于深度學習的目標檢測方法, 另一個發展分支是基于回歸的目標檢測方法. 華盛頓大學的Redmon等[6]提出了YOLO (you only look once)算法, 其核心思想是使用整張圖像作為網絡輸入, 直接在輸出層中輸出邊界框的位置及其所屬的類別. 它的訓練和檢測均在單獨的網絡中進行, 取得了較好的實時檢測效果. YOLO方法舍棄了區域備選框階段, 加快了速度, 但是定位和分類精度較低, 尤其對小目標以及比較密集的目標群檢測效果不夠理想, 召回率較低. 2017年, Redmon等[7]又提出了具有檢測速度更快、檢測精度更高和穩健性更強的YOLO v2. Ju等[8]則以YOLO v3[9]為基礎, 提出了一種改進的多尺度目標檢測算法, PASCAL VOC和KITTI數據集上的實驗結果均表明了該算法的有效性. 針對現有網絡模型在實時性方面存在的不足, He等[10]提出了實時的目標檢測模型TF-YOLO (tiny fast YOLO), 仿真結果表明, 該算法在多種設備上都可實現實時目標檢測.

針對YOLO算法定位精度低的問題, Liu等[11]提出了SSD算法, 該算法先根據錨點(anchor)提取備選框, 然后再進行分類. SSD算法將YOLO的回歸思想與Faster R-CNN的錨點機制相結合, 一次即可完成網絡訓練, 并且定位精度和分類精度相比YOLO都有大幅度提高. Bosquet等[12]提出了一種基于改進SSD模型的SAR (synthetic aperture radar)目標檢測算法, 仿真結果表明, 該算法可以實現復雜背景下SAR目標的檢測.

盡管SSD算法在特定數據集上已經取得了較高的準確率和較好的實時性, 但是, 該算法損失函數的設計未考慮正負樣本不均衡所帶來的問題, 也存在因網絡結構的缺陷而引起的小目標檢測精度不高的問題. 針對模型中出現的正負樣本失衡問題, 本文基于困難樣本挖掘原理, 在損失函數中引入調制因子; 針對因低層語義信息缺乏所導致的小目標檢測結果欠佳的問題, 采取多層特征融合的結構加以解決, 即進行預測之前先進行淺層特征圖的融合, 增強其低層的語義信息, 以期能夠提高小目標的檢測精度.

1 網絡模型

1.1

?

SSD網絡結構

本文檢測模型以傳統的基礎網絡VGG16 (visual geometry group)為基礎, 并添加深層卷積網絡而構成. 前部分淺層網絡采用卷積神經網絡提取圖像特征[10], 包括輸入層、卷積層和下采樣層; 后部分深層網絡用卷積層代替原始的全連接層. 卷積層尺寸逐層遞減, 分類和定位回歸在多尺度特征圖上完成.

1.2

?

先驗框設計

SSD網絡能夠識別多個物體, 其核心是預測固定集合的類別分數和位置偏移, 并使用應用于特征映射的小卷積濾波器的默認邊界框. SSD借鑒了Faster R-CNN中anchor的理念[5], 在特征圖上通過卷積計算產生若干覆蓋全圖的候選區域, 形成了先驗框機制. 通過為每個單元設置尺度或者長寬比不同的先驗框(預測的邊界框是以這些先驗框為基準的偏移系數), 在一定程度上減少了訓練難度. 對于每個單元的每個先驗框, 都輸出一套獨立的檢測值, 其對應的邊界框由兩部分描述: 第1部分是各個類別的置信度; 第2部分是邊界框的位置, 包含4個值(cx,cy,w,h), 分別表示邊界框的中心坐標以及寬和高. 由于先驗框在模型訓練之前就已確定, 很難與真實的標注區域完全重合. 為解決此問題, SSD算法使用位置回歸層來輸出4個位置校正參數(dx,dy,dw,dh). 先驗框經過適當變換后, 便能與真實的標注區域基本吻合.

1.3

?

引入調制因子的損失函數

損失函數用來計算模型預測值與真實值的不一致程度. 對于樣本集合(x,?y), 本文采用多任務損失函數(multi-task loss function), 可以在損失函數中完成置信度判別和位置回歸, 兩者加權求和, 得到最終的損失函數[11], 即

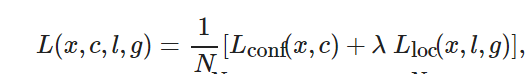
(1) ? ?

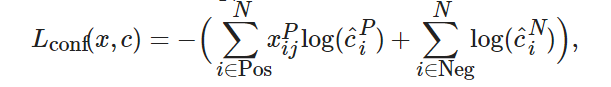
(2) ? ?

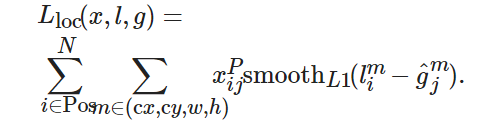
(3) ? ?

SSD算法在損失計算中, 所有的候選框可以分為正樣本和負樣本兩類, 即在所有的先驗框中, 與每個標注框有最大重疊率的被視為正樣本, 或者是與標注框的重疊大于某一閾值時, 被視為正樣本, 其他為負樣本. 然而, 在大多數圖像中, 目標所占的比例通常遠小于背景所占比例. 盡管人們對閾值選擇以及正負樣本的判斷標準有所放松, 但是仍然存在正負樣本不均衡的問題, 也就是“類別失衡”?[13]. 負樣本過多時, 容易造成負樣本損失占比過大, 進而導致正樣本的誤差損失被忽略, 不利于模型的收斂.

為解決上述問題, 本文首先將所有的待訓練先驗框進行排序, 按照置信度得分情況從大到小排列, 取前四分之一為正樣本, 其余為負樣本, 以減少負樣本比重; 然后, 在原損失函數中引入調制因子, 增加困難樣本對參數的貢獻值.

對于二分類的邏輯回歸問題, 損失函數為

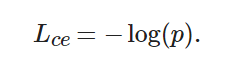
(4) ? ?

其中:?p∈(0,1)且Lce∈(0,+∞), 它代表預測框相對于標注框的置信度.?p越大,?Lce越小, 說明所訓練的樣本越容易, 該樣本越容易被正確識別, 從而對損失值的貢獻也越小; 反之,?p越小,?Lce?越大, 說明所訓練的樣本越困難, 該樣本越不容易被正確識別, 從而對損失值的貢獻也越大. 由于大量背景樣本都是容易樣本, 這些樣本疊加, 損失值之和較大, 就有可能造成“類別失衡”. 因此, 可將(1?p) 作為調制因子, 加入到原有的交叉熵損失函數中. 原有的損失函數[14]變為

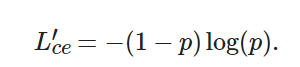
(5) ? ?

當樣本為容易樣本時,?(1?p) 越小, 損失值會在原基礎上進一步被降低, 該分類越容易, 被降低的程度也越大; 相反, 當樣本為困難樣本時,?(1?p) 越大, 分類越困難, 也有可能被誤判, 這時的調制因子相應較大, 損失值在一定程度上會被保持. 如此便實現了困難樣本的挖掘.

對于多分類問題, 仍然采用交叉熵損失函數, 區別在于p的取值不再由sigmod激活函數的輸出值所定義, 而是采用softmax函數來定義該變量, 這時p為某一類的回歸結果, 即

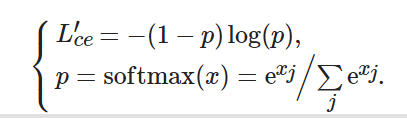
(6) ? ?

1.4?

?

引入調制因子后前向傳播函數和反向傳播函數的推導

為了讓引入調制因子后的損失函數能夠替換原有的損失函數, 下面進行損失函數的前向和反向傳播推導. 損失函數的前向傳播計算公式如下:

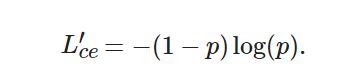
(7) ? ?

令t表示目標的類別(t∈[0,20]), 則損失函數為

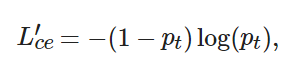
(8) ? ?

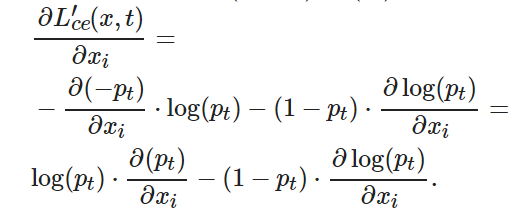
(9) ? ?

下面計算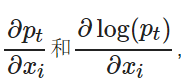?有

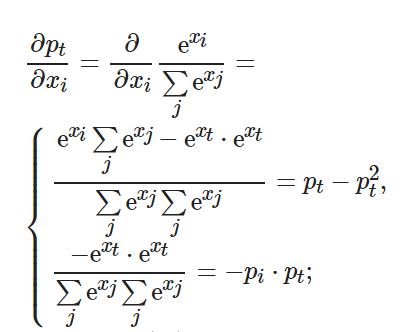
(10) ? ?

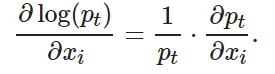
(11) ? ?

將式(10)代入(11), 可得

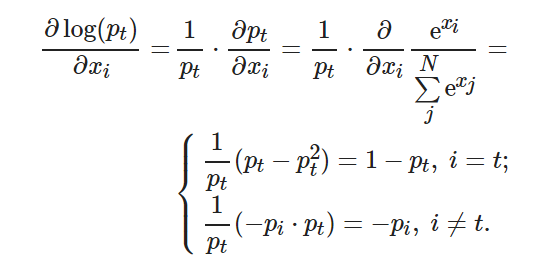
(12) ? ?

將式(10)和(12)代入(9), 可得

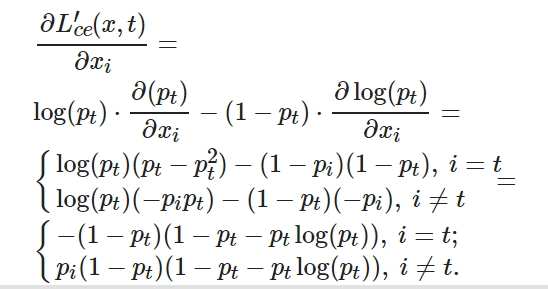
(13) ? ?

2 多層特征融合

SSD網絡參與分類和定位回歸的是多層特征圖, 這些特征圖呈金字塔結構. 下面先簡單介紹特征金字塔和圖像反卷積, 進而給出本文所設計的多層特征融合模型.

2.1

?

圖像金字塔與特征金字塔

在目標檢測中, 經常遇到多尺度問題, 通常采用圖像金字塔[15]和特征金字塔[16-17]的方法. 特征金字塔是由圖像金字塔發展而來, 它利用卷積特性, 在提取特征的同時也減小了圖像尺寸. 一個卷積神經網絡在不同的特征層, 其語義信息是不同的[18]. 特征金字塔中每一層特征都有豐富的語義信息, 但是, 如果使用金字塔中的全部特征圖, 無疑會加大運算量, 并且產生較多冗余信息. 經過對特征圖的分析, 實驗確定使用conv4-3之后的部分特征層用于目標檢測.

2.2

?

圖像反卷積

不同卷積層的特征圖有著不同的尺寸, 因此, 在進行特征融合之前, 需要對相融合的特征圖進行尺寸變換, 這就需要用到反卷積結構[19]. 反卷積, 可以簡單理解為卷積的逆過程. 即卷積層的反向傳播就是反卷積的前向傳播, 卷積層的前向傳播就是反卷積的反向傳播.

2.3

?

多層特征融合結構

SSD網絡分別在conv4??3至conv11的6層特征圖上進行分類回歸, 即使用conv4??3、conv7、conv8??2、conv9??2、conv10??2和conv11??2這6層特征圖進行檢測, 較大的特征圖用來檢測相對較小的目標, 而較小的特征圖負責檢測較大的目標[11].

通過對卷積層可視化結構圖可以看出: 特征層conv3??3由于深度較淺, 邊緣信息以及非目標干擾信息較為明顯; conv4??3和conv5??3兩層特征圖, 除了有大致的輪廓信息以外, 還包含了更多的抽象語義信息; 對于更深的conv8??2和conv9??2特征層, 基本的輪廓信息以及細節信息都丟失了, 這對于小目標的檢測效果不是很明顯. 如果加以融合, 則不僅增加了計算量, 而且對于融合后所帶來的信息增益并不明顯.

綜上, 針對SSD僅利用少量淺層特征圖來檢測目標, 缺少足夠的語義信息所導致的小目標檢測精度低的問題, 本文提取并融合淺層特征圖, 加強淺層特征圖的語義信息, 即選取conv4??3到conv7之間的特征圖進行特征融合, 多層特征融合結構如圖 1所示.

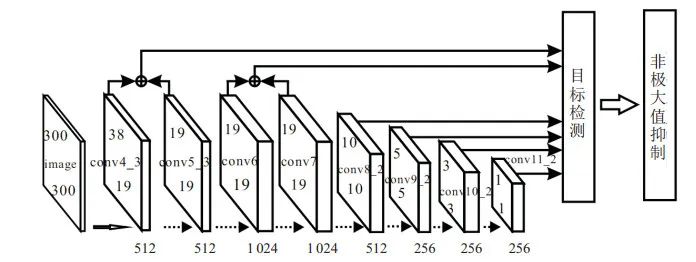
圖 1?多層特征融合結構

特征圖的融合方式主要有兩種: 通道級聯和同位置元素相加[20]. 通道級聯法增加了原有的通道數, 即描述圖像本身的特征數(通道數)增加了, 而每一特征下的信息沒有增加. 同位置元素相加法將所對應的特征圖相加, 再進行下一步的卷積操作. 該方法并未改變圖像的維度, 只是增加了每一維下的信息量, 這對最終的圖像分類顯然是有益的. 此外, 同位置元素相加法所需要的內存和參數量小于通道級聯法, 故計算量也小于通道級聯法. 所以, 本文選擇同位置元素相加法進行特征圖融合.

3 仿真實驗

3.1

?

實驗數據集

本文采用PASCAL VOC數據集(VOC2007和VOC2012)[21-22]進行訓練和測試, 該數據集組成為: 目標真值區域、類別標簽、包含目標的圖像、標注像素類別和標注像素所屬的物體. 該數據集總共分4個大類: vehicle、household、animal和person, 共計21個小類(包括1個背景類). 實驗統一圖片規格為300×300.

3.2

?

檢測模型評價指標

在對目標檢測模型進行分析評價中, 本文使用公共評價指標: 平均精確度均值(mean average precision, mAP)對模型進行評價[23]. 下面先給出準確率(precision)和召回率(recall)的定義, 進而給出mAP的定義.

準確率是指在所有正樣本中, 正確目標所占的比例, 衡量的是查準率; 召回率是指在所有真實的目標中, 被模型正確檢測出來的目標所占的比例, 衡量的是查全率. 其計算公式分別為

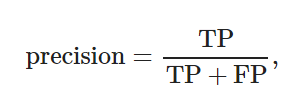
(14) ? ?

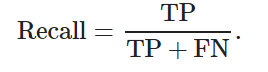
(15) ? ?

其中: TP為模型正確檢測的目標個數, FP為模型錯誤檢測的目標個數, FN為模型漏檢的正確目標個數.

以召回率為橫坐標, 以準確率為縱坐標, 二者形成的曲線稱為p-r曲線, 用來顯示檢測模型在準確率與召回率之間的平衡.?p-r曲線下的面積為該類別的平均精度(average precision, AP). 在多類別分類中, 通過求取各個類別AP的均值來計算模型整體的檢測性能指標, 其計算方法如下:

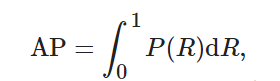
(16) ? ?

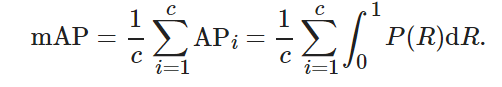
(17) ? ?

其中:?c為目標檢測的類別數, APii為第i類目標的平均精確度.

3.3

?

實驗結果與分析

為加快網絡模型的收斂速度并提升網絡性能, 本文將已訓練好的VGG16作為預訓練模型, 后續目標檢測只需在其基礎上進行微調訓練即可. 本文采用隨機梯度下降法進行模型優化, 設定初始學習速率為0.001, 權值衰減為0.000 5, 動量為0.9;卷積核大小為3×3, IOU設置為0.5;采用Pytorch深度學習框架, Python版本為Anaconda 3.6, 實驗統一圖片規格為300××300.

表 1給出了Fast R-CNN[3]、Faster R-CNN[5]、YOLO[6]、YOLO v3[9]、SSD300[11]、DSSD321[20]以及本文算法的目標檢測精度.

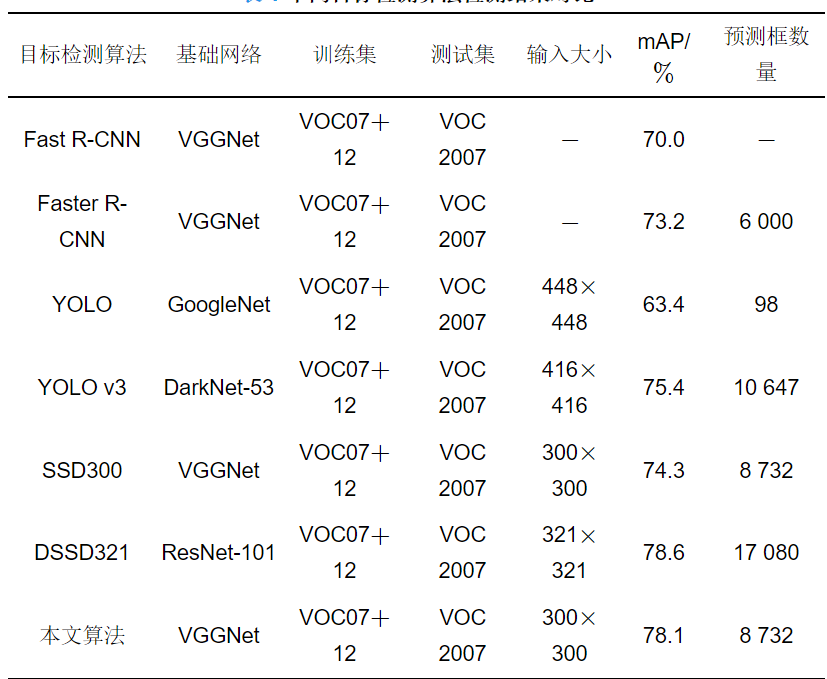
表 1?不同目標檢測算法檢測結果對比

本文算法以VGGNet為基礎網絡, 其在檢測精度方面較Fast R-CNN、Faster R-CNN、YOLO、YOLO v3和SSD300均有優勢, 但是對比基礎網絡為ResNet-101的DSSD算法而言, 精度稍有下降. 主要原因是, VGGNet網絡較淺, 而ResNet-101是非常深的網絡, 網絡越深, 目標特征越能夠更好地被提取出來, 因此檢測精度越高.

除了檢測精度外, 時間復雜度也是算法設計時需要考慮的問題. 因Fast R-CNN、Faster R-CNN、YOLO、SSD300、DSSD321算法的運行平臺與本文算法不同, 所以本文用基礎網絡的層數、基礎網絡所占內存的大小(網絡參數)和預測框的數量來衡量不同算法的時間復雜度. GoogleNet[24]、VGGNet[25]、DarkNet-53[7]和ResNet-101[26]的層數分別為22層、19層、53層和101層, 它們所占的內存分別為99.8 M、82.1 M、30.8 M和170 M.

一般而言, 層數越多, 所占內存越大, 預測框數量越多, 則認為算法的時間復雜度越高. 從表 1和上述基礎網絡參數可以看出, YOLO算法中基礎網絡的層數和所占內存略高于VGGNet, 但是預測框數量較少, 所以其計算復雜度較低. YOLO v3使用的基礎網絡是DarkNet53, 其性能可以與最先進的分類器媲美, 但是因DarkNet53需要更少的浮點運算, 所以時間復雜度較低. Fast R-CNN、Faster R-CNN、SSD300和本文算法都使用VGGNet作為基礎網絡, Faster R-CNN的預測框數量相對較少, 所以時間復雜度也較低. Fast R-CNN采用的是選擇性搜索算法, 其計算復雜度要高于采用候選框生成算法的Faster R-CNN. DSSD算法所使用的基礎網絡ResNet-101的層數遠多于本文所采用的VGGNet, 所占用的內存高出87.9 MB, 在預測框的數量上, DSSD網絡比本文算法多8 348個, 因此, DSSD算法計算復雜度最高.

圖 2給出了不同算法在20個種類的測試集上的目標檢測結果. 從實驗結果可以看出, 本文算法對于bicycle、bus、car、cat、dog、horse、motorbike、train這8類目標檢測效果較好, 都已達到了85 %以上.

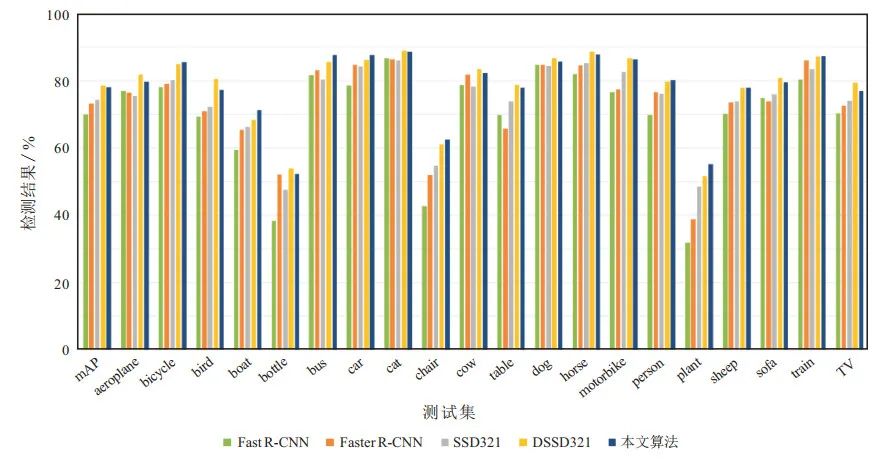
圖 2?VOC2007上各類別檢測結果對比

綜合表 1和圖 2可以看出, 本文算法在多數類別上的檢測精度均能獲得較好表現, 尤其是對于bicycle、bus、car、person等復雜背景下的目標, 相比于SSD網絡提升較為明顯, mAP分別提高了5.4 %、7.3 %、3.5 %、4 %. 但相比于DSSD網絡在bird、bottle、cow、table、sofa、TV這些類別上, 檢測精度稍有下降, 其原因可能是基礎網絡的不同而導致的特征提取信息不足.

為驗證本文算法對不同大小目標的檢測精度, 實驗中隨機選取100張圖片, 其中包含198個目標, 將其分為大、中、小三類. 由于該網絡的輸入圖像尺寸為300××300, 將圖像中的檢測目標按照其面積占圖像總面積的比例分為三類: 目標面積占圖像總面積5 %以下的認為是小目標, 目標面積占圖像面積5 %?～～?25 %的是中等目標, 目標面積占圖像總面積20 %以上的是大目標.?表 2給出了SSD算法和本文算法的檢測結果(其中: A方法為SSD算法, B方法為本文算法).

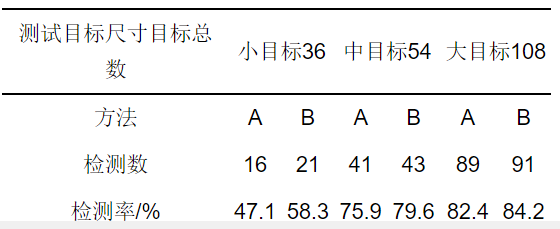
表 2?隨機檢測結果對比

由表 2可知, 本文算法對于不同尺寸的目標檢測精度均有不同程度的提高, 尤其是對于小目標的檢測率由原來的47.1 %增加到58.3 %.

圖 3給出了不同情況下的目標檢測結果, 可以看出, 本文算法對小目標的檢測、存在遮擋物的檢測以及在云霧天氣和夜間的檢測都有不錯的效果.

圖 3?不同條件下的目標檢測結果

4 結論

針對正負樣本不均衡所導致的低分類精度等問題, 本文在原SSD算法的損失函數中引入調制因子, 減小簡單樣本的損失權值, 增加困難樣本的損失值所占比重, 以達到提高復雜背景下目標檢測精度的目的. 同時, 調制因子的引入可以減少原模型交叉熵損失函數浪費在容易樣本上的計算力, 使得損失函數可以更快地跳過原有容易樣本的簡單數據, 更快地進入后面困難樣本的計算, 從而加快訓練階段的收斂速度. 其次, 針對因網絡結構的缺陷而引起的小目標檢測精度欠佳問題, 本文采取一種基于特征金字塔的多層特征檢測結構, 以增強用于檢測小目標的淺層特征圖語義信息. 實驗結果表明, 本文算法在多種類別目標的檢測精度上都較SSD算法有了不同程度的提高, 尤其是在小目標檢測識別方面, 檢測精度顯著提高.

編輯:黃飛

?