有個事情可能會讓初學者驚訝:神經網絡模型并不復雜!『神經網絡』這個詞讓人覺得很高大上,但實際上神經網絡算法要比人們想象的簡單。
這篇文章完全是為新手準備的。我們會通過用Python從頭實現一個神經網絡來理解神經網絡的原理。本文的脈絡是:
介紹了神經網絡的基本結構——神經元;
在神經元中使用S型激活函數;
神經網絡就是連接在一起的神經元;
構建了一個數據集,輸入(或特征)是體重和身高,輸出(或標簽)是性別;
學習了損失函數和均方差損失;
訓練網絡就是最小化其損失;
用反向傳播方法計算偏導;
用隨機梯度下降法訓練網絡。 ?
磚塊:神經元
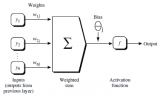
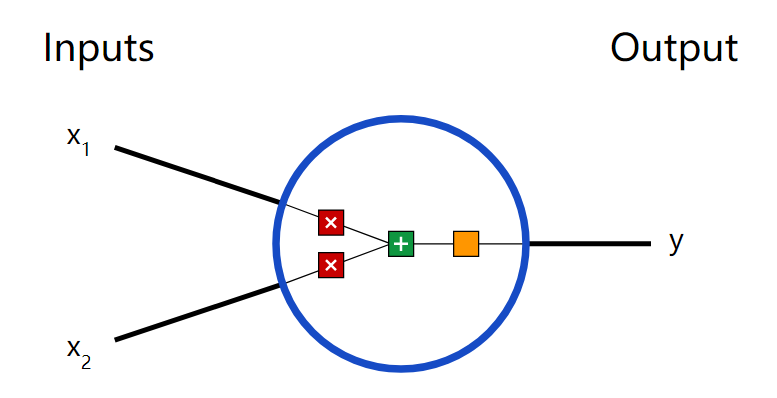
首先讓我們看看神經網絡的基本單位,神經元。神經元接受輸入,對其做一些數據操作,然后產生輸出。例如,這是一個2-輸入神經元:
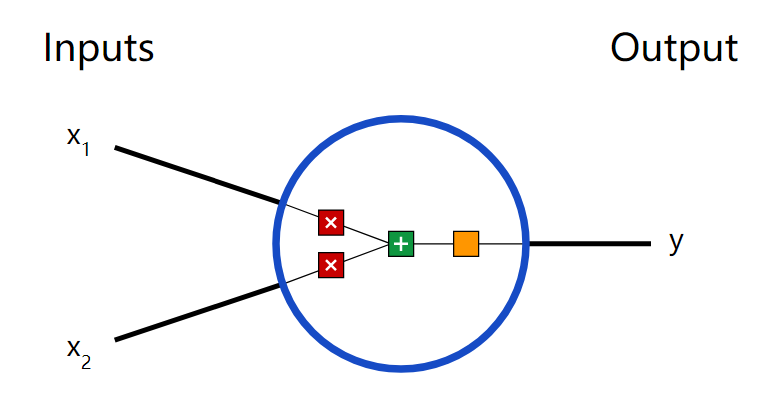
這里發生了三個事情。首先,每個輸入都跟一個權重相乘(紅色):
然后,加權后的輸入求和,加上一個偏差b(綠色):
最后,這個結果傳遞給一個激活函數f:
激活函數的用途是將一個無邊界的輸入,轉變成一個可預測的形式。常用的激活函數就就是S型函數:
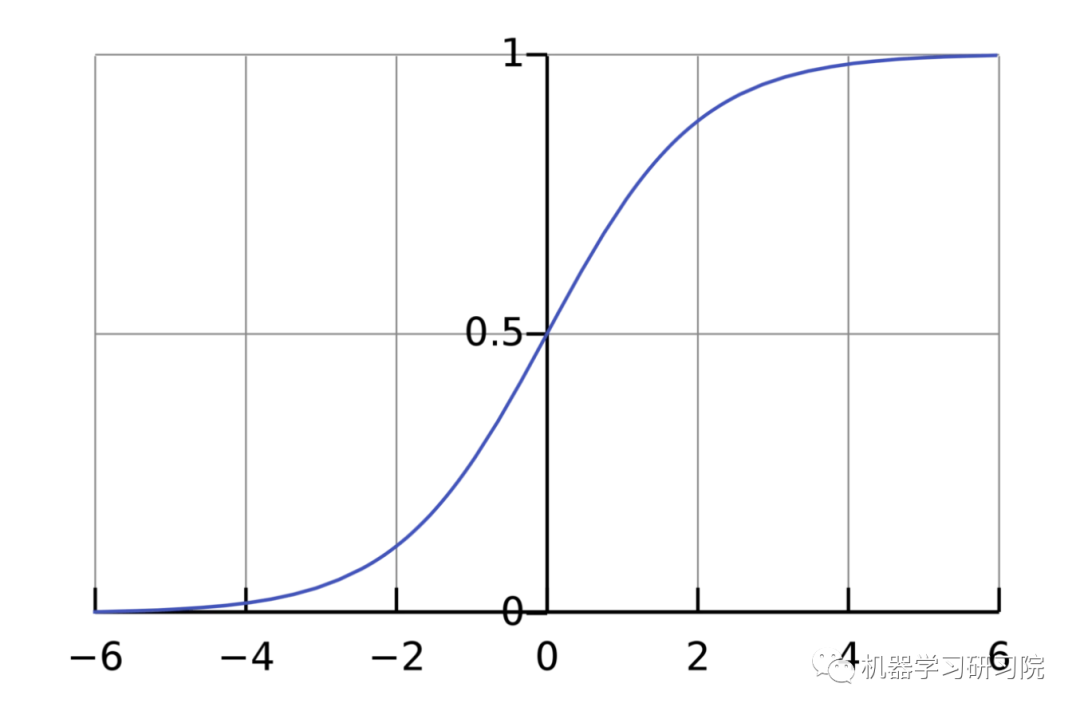
S型函數的值域是(0, 1)。簡單來說,就是把(?∞, +∞)壓縮到(0, 1) ,很大的負數約等于0,很大的正數約等于1。
一個簡單的例子
假設我們有一個神經元,激活函數就是S型函數,其參數如下:
就是以向量的形式表示。現在,我們給這個神經元一個輸入。我們用點積來表示:
當輸入是[2, 3]時,這個神經元的輸出是0.999。給定輸入,得到輸出的過程被稱為前饋(feedforward)。
編碼一個神經元
讓我們來實現一個神經元!用Python的NumPy庫來完成其中的數學計算:
?
?
import?numpy?as?np def?sigmoid(x): ??#?我們的激活函數:?f(x)?=?1?/?(1?+?e^(-x)) ??return?1?/?(1?+?np.exp(-x)) class?Neuron: ??def?__init__(self,?weights,?bias): ????self.weights?=?weights ????self.bias?=?bias ??def?feedforward(self,?inputs): ????#?加權輸入,加入偏置,然后使用激活函數 ????total?=?np.dot(self.weights,?inputs)?+?self.bias ????return?sigmoid(total) weights?=?np.array([0,?1])?#?w1?=?0,?w2?=?1 bias?=?4???????????????????#?b?=?4 n?=?Neuron(weights,?bias) x?=?np.array([2,?3])???????#?x1?=?2,?x2?=?3 print(n.feedforward(x))????#?0.9990889488055994
?
?
還記得這個數字嗎?就是我們前面算出來的例子中的0.999。
把神經元組裝成網絡
所謂的神經網絡就是一堆神經元。這就是一個簡單的神經網絡:
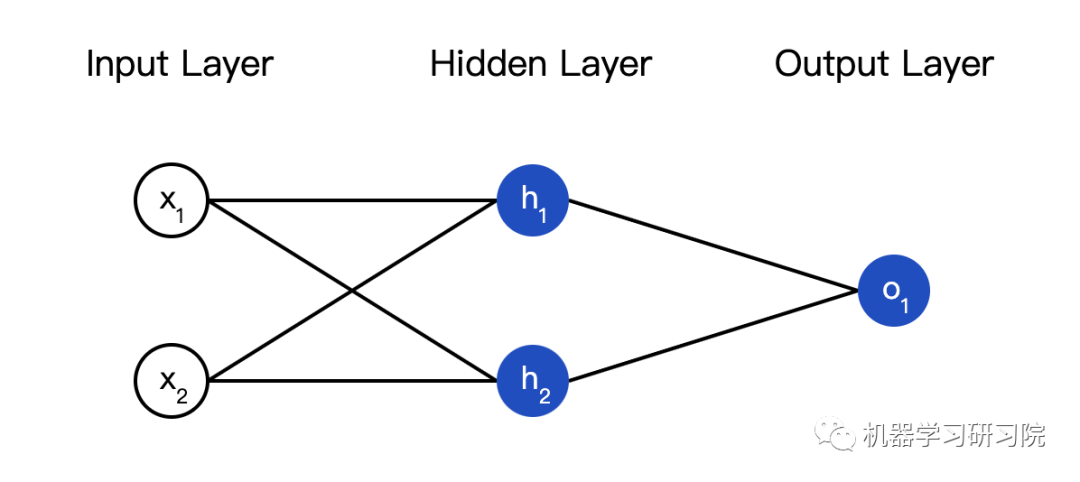
這個網絡有兩個輸入,一個有兩個神經元(?和?)的隱藏層,以及一個有一個神經元(?) )的輸出層。要注意,?的輸入就是?和??的輸出,這樣就組成了一個網絡。
隱藏層就是輸入層和輸出層之間的層,隱藏層可以是多層的。
例子:前饋
我們繼續用前面圖中的網絡,假設每個神經元的權重都是??,截距項也相同??,激活函數也都是S型函數。分別用?表示相應的神經元的輸出。
當輸入??時,會得到什么結果?
這個神經網絡對輸入的輸出是0.7216,很簡單。
一個神經網絡的層數以及每一層中的神經元數量都是任意的。基本邏輯都一樣:輸入在神經網絡中向前傳輸,最終得到輸出。接下來,我們會繼續使用前面的這個網絡。
編碼神經網絡:前饋
接下來我們實現這個神經網絡的前饋機制,還是這個圖:
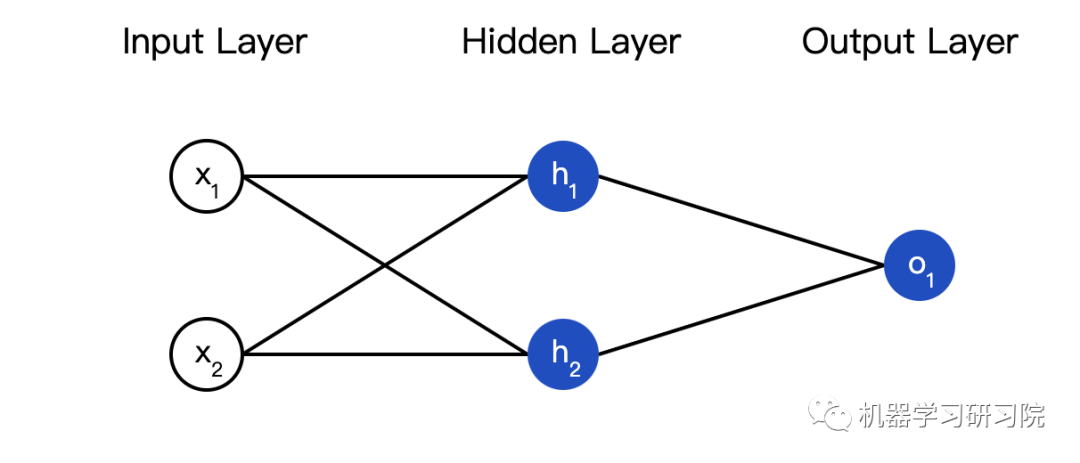
?
?
import?numpy?as?np #?...?code?from?previous?section?here class?OurNeuralNetwork: ??''' ??A?neural?network?with: ????-?2?inputs ????-?a?hidden?layer?with?2?neurons?(h1,?h2) ????-?an?output?layer?with?1?neuron?(o1) ??Each?neuron?has?the?same?weights?and?bias: ????-?w?=?[0,?1] ????-?b?=?0 ??''' ??def?__init__(self): ????weights?=?np.array([0,?1]) ????bias?=?0 ????#?這里是來自前一節的神經元類 ????self.h1?=?Neuron(weights,?bias) ????self.h2?=?Neuron(weights,?bias) ????self.o1?=?Neuron(weights,?bias) ??def?feedforward(self,?x): ????out_h1?=?self.h1.feedforward(x) ????out_h2?=?self.h2.feedforward(x) ????#?o1的輸入是h1和h2的輸出 ????out_o1?=?self.o1.feedforward(np.array([out_h1,?out_h2])) ????return?out_o1 network?=?OurNeuralNetwork() x?=?np.array([2,?3]) print(network.feedforward(x))?#?0.7216325609518421
?
?
結果正確,看上去沒問題。
訓練神經網絡 第一部分
現在有這樣的數據:
?
| 姓名 | 體重(磅) | 身高 (英寸) | 性別 |
|---|---|---|---|
| Alice | 133 | 65 | F |
| Bob | 160 | 72 | M |
| Charlie | 152 | 70 | M |
| Diana | 120 | 60 | F |
?
接下來我們用這個數據來訓練神經網絡的權重和截距項,從而可以根據身高體重預測性別:
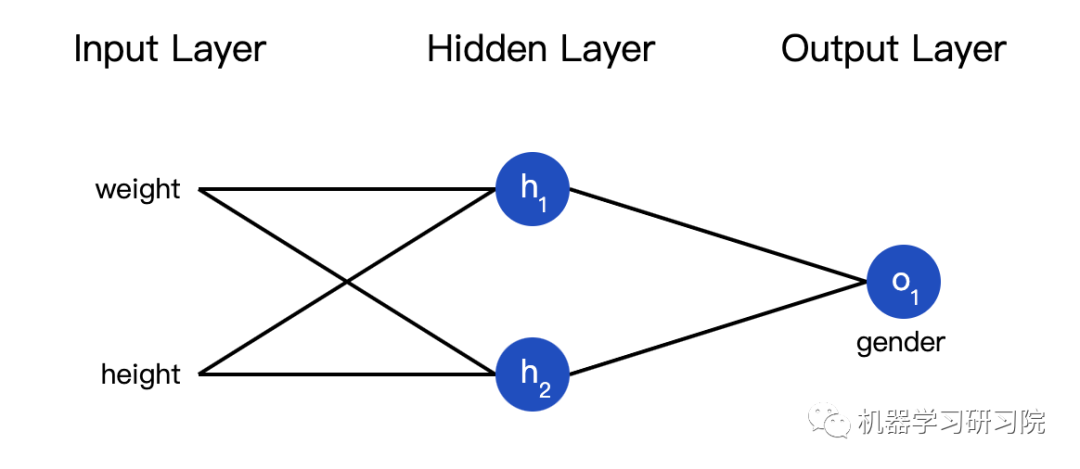
我們用0和1分別表示男性(M)和女性(F),并對數值做了轉化:
?
| 姓名 | 體重 (減 135) | 身高 (減 66) | 性別 |
|---|---|---|---|
| Alice | -2 | -1 | 1 |
| Bob | 25 | 6 | 0 |
| Charlie | 17 | 4 | 0 |
| Diana | -15 | -6 | 1 |
?
我這里是隨意選取了135和66來標準化數據,通常會使用平均值。
損失
在訓練網絡之前,我們需要量化當前的網絡是『好』還是『壞』,從而可以尋找更好的網絡。這就是定義損失的目的。
我們在這里用平均方差(MSE)損失:?,讓我們仔細看看:
是樣品數,這里等于4(Alice、Bob、Charlie和Diana)。
表示要預測的變量,這里是性別。
是變量的真實值(『正確答案』)。例如,Alice的??就是1(男性)。
變量的預測值。這就是我們網絡的輸出。
被稱為方差(squared error)。我們的損失函數就是所有方差的平均值。預測效果越好,損失就越少。
更好的預測 = 更少的損失!
訓練網絡 = 最小化它的損失。
損失計算例子
假設我們的網絡總是輸出0,換言之就是認為所有人都是男性。損失如何?
?
| Name | y_true | y_pred | (y_true - y_pred)^2 |
|---|---|---|---|
| Alice | 1 | 0 | 1 |
| Bob | 0 | 0 | 0 |
| Charlie | 0 | 0 | 0 |
| Diana | 1 | 0 | 1 |
?
代碼:MSE損失
下面是計算MSE損失的代碼:
?
?
import?numpy?as?np def?mse_loss(y_true,?y_pred): ??#?y_true?and?y_pred?are?numpy?arrays?of?the?same?length. ??return?((y_true?-?y_pred)?**?2).mean() y_true?=?np.array([1,?0,?0,?1]) y_pred?=?np.array([0,?0,?0,?0]) print(mse_loss(y_true,?y_pred))?#?0.5
?
?
如果你不理解這段代碼,可以看看NumPy的快速入門中關于數組的操作。
好的,繼續。
訓練神經網絡 第二部分
現在我們有了一個明確的目標:最小化神經網絡的損失。通過調整網絡的權重和截距項,我們可以改變其預測結果,但如何才能逐步地減少損失?
這一段內容涉及到多元微積分,如果不熟悉微積分的話,可以跳過這些數學內容。
為了簡化問題,假設我們的數據集中只有Alice:
假設我們的網絡總是輸出0,換言之就是認為所有人都是男性。損失如何?
?
| 姓名 | 體重 (減 135) | 身高 (減 66) | Gender |
|---|---|---|---|
| Alice | -2 | -1 | 1 |
?
那均方差損失就只是Alice的方差:
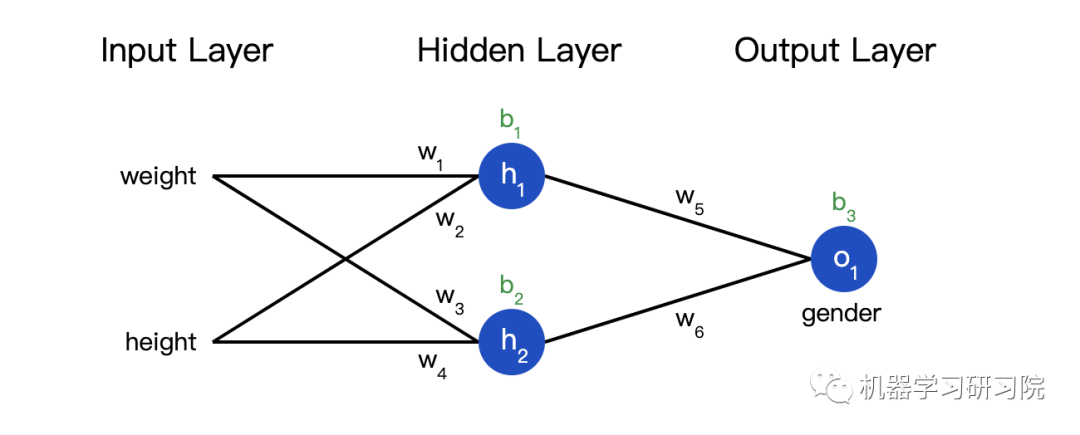
也可以把損失看成是權重和截距項的函數。讓我們給網絡標上權重和截距項:

這樣我們就可以把網絡的損失表示為:
假設我們要優化??,當我們改變??時,損失??會怎么變化?可以用??來回答這個問題,怎么計算?
接下來的數據稍微有點復雜,別擔心,準備好紙和筆。
首先,讓我們用來改寫這個偏導數:
因為我們已經知道??,所以我們可以計算
現在讓我們來搞定??。分別是其所表示的神經元的輸出,我們有:
由于??只會影響??(不會影響??),所以:
對??,我們也可以這么做:
在這里,?是身高,?是體重。這是我們第二次看到??(S型函數的導數)了。求解:
稍后我們會用到這個??。
我們已經把?分解成了幾個我們能計算的部分:
這種計算偏導的方法叫『反向傳播算法』(backpropagation)。
好多數學符號,如果你還沒搞明白的話,我們來看一個實際例子。
例子:計算偏導數
我們還是看數據集中只有Alice的情況:
?
| Name | ? | ? | ? |
|---|---|---|---|
| Alice | 1 | 0 | 1 |
| 姓名 | 身高 (minus 135) | 體重 (minus 66) | Gender |
|---|---|---|---|
| Alice | -2 | -1 | 1 |
?
把所有的權重和截距項都分別初始化為1和0。在網絡中做前饋計算:
網絡的輸出是??,對于Male(0)或者Female(1)都沒有太強的傾向性。算一下
提示:前面已經得到了S型激活函數的導數??。
搞定!這個結果的意思就是增加也會隨之輕微上升。
訓練:隨機梯度下降
現在訓練神經網絡已經萬事俱備了!我們會使用名為隨機梯度下降法的優化算法來優化網絡的權重和截距項,實現損失的最小化。核心就是這個更新等式:
是一個常數,被稱為學習率,用于調整訓練的速度。我們要做的就是用??減去
如果??是正數,??變小,?會下降。
如果???是負數,??會變大,??會上升。
如果我們對網絡中的每個權重和截距項都這樣進行優化,損失就會不斷下降,網絡性能會不斷上升。
我們的訓練過程是這樣的:
從我們的數據集中選擇一個樣本,用隨機梯度下降法進行優化——每次我們都只針對一個樣本進行優化;
計算每個權重或截距項對損失的偏導(例如?、?等);
用更新等式更新每個權重和截距項;
重復第一步;
代碼:一個完整的神經網絡
我們終于可以實現一個完整的神經網絡了:
?
| 姓名 | 身高 (減 135) | 體重 (減 66) | Gender |
|---|---|---|---|
| Alice | -2 | -1 | 1 |
| Bob | 25 | 6 | 0 |
| Charlie | 17 | 4 | 0 |
| Diana | -15 | -6 | 1 |
?
?
?
import?numpy?as?np def?sigmoid(x): ??#?Sigmoid?activation?function:?f(x)?=?1?/?(1?+?e^(-x)) ??return?1?/?(1?+?np.exp(-x)) def?deriv_sigmoid(x): ??#?Derivative?of?sigmoid:?f'(x)?=?f(x)?*?(1?-?f(x)) ??fx?=?sigmoid(x) ??return?fx?*?(1?-?fx) def?mse_loss(y_true,?y_pred): ??# y_true和y_pred是相同長度的numpy數組。 ??return?((y_true?-?y_pred)?**?2).mean() class?OurNeuralNetwork: ??''' ??A?neural?network?with: ????-?2?inputs ????-?a?hidden?layer?with?2?neurons?(h1,?h2) ????-?an?output?layer?with?1?neuron?(o1) ??***?免責聲明?***: ????下面的代碼是為了簡單和演示,而不是最佳的。 ????真正的神經網絡代碼與此完全不同。不要使用此代碼。 ????相反,讀/運行它來理解這個特定的網絡是如何工作的。 ??''' ??def?__init__(self): ????#?權重,Weights ????self.w1?=?np.random.normal() ????self.w2?=?np.random.normal() ????self.w3?=?np.random.normal() ????self.w4?=?np.random.normal() ????self.w5?=?np.random.normal() ????self.w6?=?np.random.normal() ????#?截距項,Biases ????self.b1?=?np.random.normal() ????self.b2?=?np.random.normal() ????self.b3?=?np.random.normal() ??def?feedforward(self,?x): ????# X是一個有2個元素的數字數組。 ????h1?=?sigmoid(self.w1?*?x[0]?+?self.w2?*?x[1]?+?self.b1) ????h2?=?sigmoid(self.w3?*?x[0]?+?self.w4?*?x[1]?+?self.b2) ????o1?=?sigmoid(self.w5?*?h1?+?self.w6?*?h2?+?self.b3) ????return?o1 ??def?train(self,?data,?all_y_trues): ????''' ????-?data?is?a?(n?x?2)?numpy?array,?n?=?#?of?samples?in?the?dataset. ????-?all_y_trues?is?a?numpy?array?with?n?elements. ??????Elements?in?all_y_trues?correspond?to?those?in?data. ????''' ????learn_rate?=?0.1 ????epochs?=?1000?#?遍歷整個數據集的次數 ????for?epoch?in?range(epochs): ??????for?x,?y_true?in?zip(data,?all_y_trues): ????????#?---?做一個前饋(稍后我們將需要這些值) ????????sum_h1?=?self.w1?*?x[0]?+?self.w2?*?x[1]?+?self.b1 ????????h1?=?sigmoid(sum_h1) ????????sum_h2?=?self.w3?*?x[0]?+?self.w4?*?x[1]?+?self.b2 ????????h2?=?sigmoid(sum_h2) ????????sum_o1?=?self.w5?*?h1?+?self.w6?*?h2?+?self.b3 ????????o1?=?sigmoid(sum_o1) ????????y_pred?=?o1 ????????#?---?計算偏導數。 ????????#?---?Naming:?d_L_d_w1?represents?"partial?L?/?partial?w1" ????????d_L_d_ypred?=?-2?*?(y_true?-?y_pred) ????????#?Neuron?o1 ????????d_ypred_d_w5?=?h1?*?deriv_sigmoid(sum_o1) ????????d_ypred_d_w6?=?h2?*?deriv_sigmoid(sum_o1) ????????d_ypred_d_b3?=?deriv_sigmoid(sum_o1) ????????d_ypred_d_h1?=?self.w5?*?deriv_sigmoid(sum_o1) ????????d_ypred_d_h2?=?self.w6?*?deriv_sigmoid(sum_o1) ????????#?Neuron?h1 ????????d_h1_d_w1?=?x[0]?*?deriv_sigmoid(sum_h1) ????????d_h1_d_w2?=?x[1]?*?deriv_sigmoid(sum_h1) ????????d_h1_d_b1?=?deriv_sigmoid(sum_h1) ????????#?Neuron?h2 ????????d_h2_d_w3?=?x[0]?*?deriv_sigmoid(sum_h2) ????????d_h2_d_w4?=?x[1]?*?deriv_sigmoid(sum_h2) ????????d_h2_d_b2?=?deriv_sigmoid(sum_h2) ????????#?---?更新權重和偏差 ????????#?Neuron?h1 ????????self.w1?-=?learn_rate?*?d_L_d_ypred?*?d_ypred_d_h1?*?d_h1_d_w1 ????????self.w2?-=?learn_rate?*?d_L_d_ypred?*?d_ypred_d_h1?*?d_h1_d_w2 ????????self.b1?-=?learn_rate?*?d_L_d_ypred?*?d_ypred_d_h1?*?d_h1_d_b1 ????????#?Neuron?h2 ????????self.w3?-=?learn_rate?*?d_L_d_ypred?*?d_ypred_d_h2?*?d_h2_d_w3 ????????self.w4?-=?learn_rate?*?d_L_d_ypred?*?d_ypred_d_h2?*?d_h2_d_w4 ????????self.b2?-=?learn_rate?*?d_L_d_ypred?*?d_ypred_d_h2?*?d_h2_d_b2 ????????#?Neuron?o1 ????????self.w5?-=?learn_rate?*?d_L_d_ypred?*?d_ypred_d_w5 ????????self.w6?-=?learn_rate?*?d_L_d_ypred?*?d_ypred_d_w6 ????????self.b3?-=?learn_rate?*?d_L_d_ypred?*?d_ypred_d_b3 ??????#?---?在每次epoch結束時計算總損失? ??????if?epoch?%?10?==?0: ????????y_preds?=?np.apply_along_axis(self.feedforward,?1,?data) ????????loss?=?mse_loss(all_y_trues,?y_preds) ????????print("Epoch?%d?loss:?%.3f"?%?(epoch,?loss)) #?定義數據集 data?=?np.array([ ??[-2,?-1],??#?Alice ??[25,?6],???#?Bob ??[17,?4],???#?Charlie ??[-15,?-6],?#?Diana ]) all_y_trues?=?np.array([ ??1,?#?Alice ??0,?#?Bob ??0,?#?Charlie ??1,?#?Diana ]) #?訓練我們的神經網絡! network?=?OurNeuralNetwork() network.train(data,?all_y_trues)
?
?
隨著網絡的學習,損失在穩步下降。
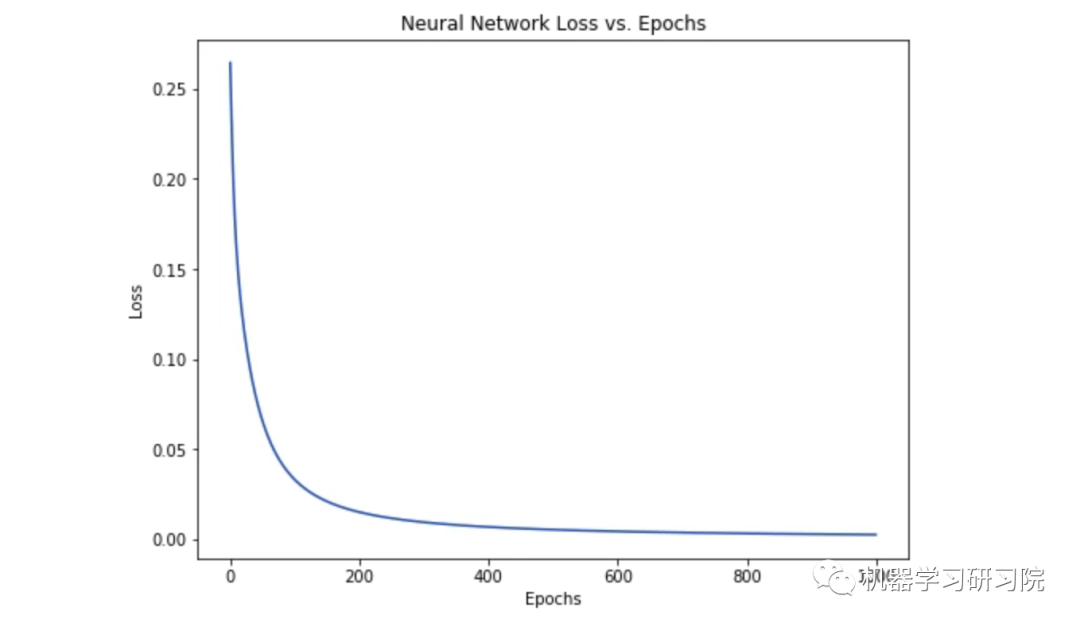
現在我們可以用這個網絡來預測性別了:
?
?
#?做一些預測
emily?=?np.array([-7,?-3])?#?128?磅,?63?英寸
frank?=?np.array([20,?2])??#?155?磅,?68?英寸
print("Emily:?%.3f"?%?network.feedforward(emily))?#?0.951?-?F
print("Frank:?%.3f"?%?network.feedforward(frank))?#?0.039?-?M
?
?

接下來?

搞定了一個簡單的神經網絡,快速回顧一下:
介紹了神經網絡的基本結構——神經元;
在神經元中使用S型激活函數;
神經網絡就是連接在一起的神經元;
構建了一個數據集,輸入(或特征)是體重和身高,輸出(或標簽)是性別;
學習了損失函數和均方差損失;
訓練網絡就是最小化其損失;
用反向傳播方法計算偏導;
用隨機梯度下降法訓練網絡;
接下來你還可以:
用機器學習庫實現更大更好的神經網絡,例如TensorFlow、Keras和PyTorch;
其他類型的激活函數;
其他類型的優化器;
學習卷積神經網絡,這給計算機視覺領域帶來了革命; 學習遞歸神經網絡,常用于自然語言處理;
作者:Victor Zhou?
編輯:黃飛
 電子發燒友App
電子發燒友App












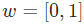












評論