本文討論了五個主要的先驗假設以及如何突破這些假設限制并進一步提升機器學習效果的方法。在此基礎上我們提出了機器學習自動化的概念以及SLeM框架。SLeM為機器學習自動化研究提供了一個形式化/模型化/科學化的研究框架和途徑。現有應用表明SLeM是一個強大而有效的工具，同時它也處于快速持續的發展過程中。

以深度學習為代表的人工智能已經突破了從“不能用”到“可以用”的技術拐點，但是從“可以用”到“很好用”，還有很長的路要走。人工智能最核心的技術是機器學習，即從給定的數據集中總結規律或尋求表征，可以概括為圖1所示的公式。

這個模型概括了機器學習解決問題的一般步驟：首先我們需要選擇一個較大范圍的、可能包含數據規律或表示函數的假設空間，然后指定一個損失度量，在該度量下，我們在假設空間中找一個函數，它能夠將函數在給定數據集上的平均損失極小化。極小化數據集上的平均損失這一目標被稱為“數據擬合項”，相應的方法即為經驗風險極小化。然而，僅通過極小化數據擬合項來尋找解常常是不適定的，因而必須添加某些額外的約束，新增加的希望滿足的這些約束構成“正則項”。極小化數據擬合項與正則項之和被稱為“正則化方法”，它構成了機器學習的最基本模型。

機器學習有先驗假設

使用機器學習時，我們總是自覺或不自覺地施加一些假設，例如：

損失度量的獨立性假設。我們總是習慣使用像最小二乘或者交叉熵這樣確定的度量作為損失，而不把損失度量的選擇與我們要解決的具體問題關聯起來，更沒有依據面臨的問題自適應地確定最優的損失度量。

假設空間的大容量假設。我們總是自然地認為，我們選擇使用的機器架構（例如用一個20層的深度學習架構）已經包含我們期望找到的解，或者說，已經包含數據所蘊含的規律。這個假設顯然是保證機器學習成功的前提。我們通常都很自信：我們選的架構是合理的，是包含所要找的解的。

訓練數據的完備性假設。我們使用機器學習時，總期望訓練機器的數據是非常充分的、足夠多的、高質量的。這個假定常常是我們選擇機器學習方法的前提和原由。

正則子的先驗決定論假設。為了使機器學習產生的決策函數有期望的性質，施加一定的正則約束是必須的。例如我們已習慣于使用L2正則保證光滑性，使用L1正則保證稀疏性，使用TV正則保持圖像邊緣稀疏性，等等。人們一般認為，正則項的形式是由先驗決定的，我們在使用機器學習時，能夠根據先驗事先加以確定。這個假定的本質是，我們已經能夠將問題的先驗抽象出知識，而且能夠正確地以“正則子”形式建模。之所以把這一認識叫作假設，是因為我們其實并不知道應用中所選擇的正則子是否已經正確地對先驗進行了建模。

分析框架的歐氏假設。當我們訓練深度網絡架構時，會自然地選擇使用BP或ADAM這樣類型的優化算法。為什么？這是因為這些算法都經過了嚴格的理論評判（收斂性、穩定性、復雜性等）。評判算法即把算法放在一個特定的數學框架內進行分析而得出結論的活動。我們通常把評判算法放在可使用二范數、正交性這樣的歐氏框架中。這樣的假設本質上限定了可用算法的類型和可用機器的架構（損失函數、正則項等）。在這樣的假設下，我們并不能處理和敢于使用更復雜的非歐氏空間算法和機器學習架構。

這5個假設相當大程度上決定了機器學習的效能。

如何突破機器學習的先驗假設

已有大量工作聚焦于如何突破機器學習的這些假設。以下是筆者團隊近年來在這方面的一些代表性工作。

關于分析框架歐氏假設

我們認為，歐氏空間之所以被廣泛使用，根本原因是我們在算法分析中能夠使用歐式架構(a+b)2=a2+b2 +2ab，在這樣的架構下，任何一個算法的性能（如收斂性）都和目標函數的凸性發生聯系。因此，要沖破目標函數的凸性假設，本質上就是要沖破歐氏假設。筆者1989年及1991年的工作打開了用非歐氏架構工具研究非歐氏算法的可能性，近年來這些工具得到廣泛應用。從這些研究中可看出，沖破歐氏假設的途徑在于應用Banach空間幾何學。

關于損失獨立性假設

損失有兩個功能，一是度量選定的函數在給定數據／數據集上的擬合程度，二是度量一個函數表示的精度。盡管在有導師學習和無導師學習模式下，它們可能有著不同的表現形式，但它的選擇本質上都應該是與問題相關的。事實上，如果我們把問題的標簽和特征用式(1)描述的觀察模型來理解，

y=fθ(x)+e????????????????(1)

那么，標簽由一個固定的規律加上一個噪聲得到，這個噪聲就是數據獲取的環境。根據概率公式，我們很容易看到，最好標簽出現的概率完全由它的誤差環境決定。這給我們一個很重要的啟示：機器學習的最佳度量應該由誤差決定。我們通過實驗發現，如果假定誤差是白噪聲，那么最優的恢復度量確實是最小二乘。但如果噪聲是其他類型，最優恢復度量就不再是最小二乘了。

給定一個具體的誤差分布形式，我們能確定出一個特定的最佳恢復度量，這樣的方法稱為誤差建模原理。對于任何機器學習問題，通過研究它生成的誤差形式，就能獲得一定意義下最優的損失度量，而在該度量下找到機器學習的經驗函數才是最好的。筆者團隊已有很多成功應用誤差建模原理的案例，最典型的是根據這一原理成功研發微劑量CT，實現了將CT幅射劑量降低到微劑量水平。

一般來說，我們并不知道要解決的問題處于一個什么樣的誤差環境，這種情況下，我們可以運用高斯混合來逼近。事實上，任何一個分式函數都能以多個高斯分布函數之和來逼近。據此，我們證明，不同的高斯混合導致不同加權的“加權最小二乘”最優度量。這給出一個非常有用的提示：當我們不知道誤差的真正形式時，加權最小二乘是一個不錯的選擇。

關于假設空間的大容量假設

如何設計一個機器架構使希望找到的問題解確在其中？我們提出了一個非常基礎的方法：先構建一個含大量超參數的粗糙模型（叫模型族）來刻畫問題解的范圍，然后求解“模型族”構成解決問題的“算法族”，再把“算法族”自適應化展開成一個深度網絡架構，它的參數包含模型簇和算法簇中的所有參數并且允許每個迭代步不同；最后應用數據來訓練這樣形成的網絡產生問題的解。這樣的一般化方法稱為模型驅動的深度學習。模型驅動的深度學習表面上看是解決深度學習的架構設計問題，但本質上是在深度學習過程中逐步設置包含解的最小假設空間來突破假設空間的大容量假設。這一方法不同于傳統的數學建模方法（要求精確建模），前者只要求對問題解的整體范圍進行刻畫；它也不同于傳統的深度學習（沒有融入物理機制），模型驅動的深度學習具有明確的物理機制解釋和嚴密的數學基礎。由此回避了深度學習架構設計難的問題，從而使機器學習架構能夠在理論指導及可解釋的意義下進行設計，如圖2所示。

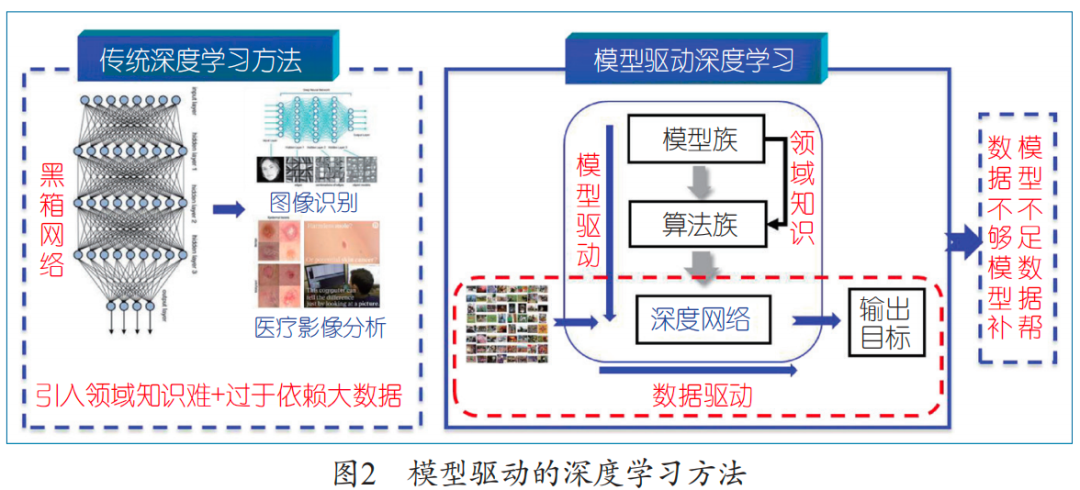
筆者團隊2018年在《國家科學評論》（NSR）上正式提出了這一方法。使用這一方法，筆者團隊提出了大家熟知的ADMM CS-Net深度學習架構。該架構是實現壓縮感知的一個普遍有效的深度學習模型，已經得到普遍應用，并被認為是一個開創性的、奠基性的網絡。它的重要意義是在最優化理論和深度學習網絡設計之間搭建起一座橋梁，尤其是它能夠比傳統的壓縮感知模型、正則化方法更好地處理稀疏性問題。

關于正則子先驗決定論假設

突破正則先驗假設是非常困難的，因為無論怎么選擇, 也很能保證所選的正則項能真實地反映先驗。我們分析認為，問題的困難性出在“正則化方法是在知識層面建模先驗”上，要擺脫困境，出路是直接從數據中學習先險。為此，我們提出并建立了一個稱為“隱正則化理論”的方法。我們證明：正則化問題的解在一定條件下能夠等價于一個含近點投影算子的不動點方程，從而可自然地迭代求解并展開成一個模型驅動的深度學習網絡，而近點投影算子與正則項是能夠惟一相互決定的。這樣，代替設置正則項，我們可以通過數據學習近點投影算子，從而起到與正則化方法一樣的效果。值得注意的是，設定正則項是利用先驗知識，而隱正則化是從數據中抽取知識，融入學習過程，因此在原理上具有重要的意義。

關于數據完備性假設

數據的完備性和高質量是保證機器學習效果的關鍵。課程學習的想法能夠把學習過程與人類受教育的過程類比，從而以“先易后難”分步處理的方式應對不完備的數據（正如小學生先學簡單的內容再學更難的內容一樣）。過去十余年，筆者團隊完整建立了“課程自步學習”的理論與算法體系，將類課程學習標準化成一個十分有效的處理不完備數據的機器學習方法。

總的來說，我們過去多年的工作是發展一些科學原理，希望在這些原理指導下，機器學習的先驗假設能得以突破。我們的工作主要是：利用Banach幾何工具來突破分析的歐氏假設，利用誤差建模原理來突破損失的獨立性假設，利用模型驅動的深度學習方式來突破假設空間的大容量假設，利用隱正則化方法來突破正則先驗假設，利用課程自步學習來突破數據的完備性假設（見圖3）。所有這些工作都被證明是很有效的。

機器學習要實現自動化

機器學習的當前發展基本上仍處于“人工”階段：在數據層面，仍需要人工收集數據、標注數據，且需要人工決定哪些數據用作訓練，哪些數據用作測試；在模型和算法層面，人們還大都只是從已知的模型和算法中選擇一個架構和算法，基本上處于被動選擇狀態；在應用層面，我們還是一個任務一個模型，做不到任務自切換、環境自適應。顯然，要想把人工智能從“人工化”推向“自主化”，中間必須要邁過一個關口，即機器學習要“自動化”，其過程如圖4所示。

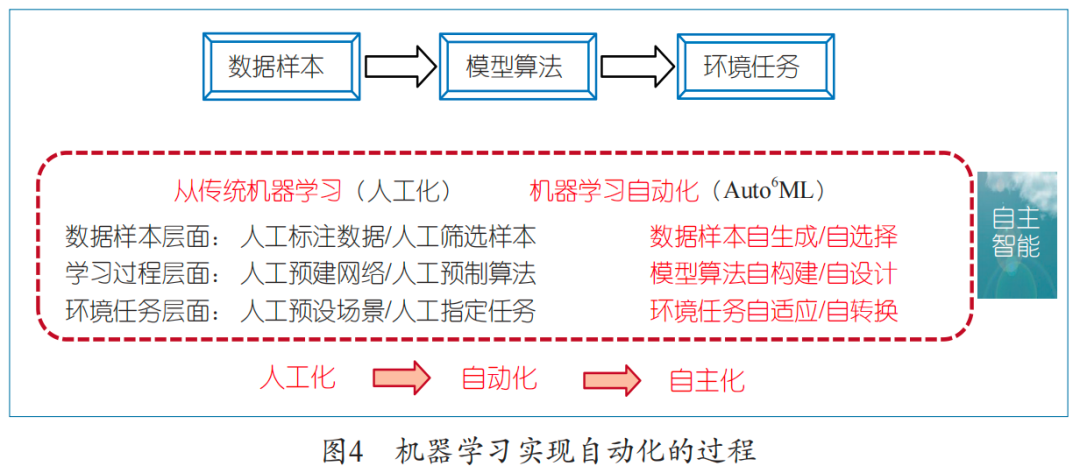
我們認為，機器學習自動化首先要至少實現六個方面的自動化。一是數據自動化 ：實現數據的自生成、自選擇。要根據目標任務需要或少量元數據（標準、高質量數據）的引導，實現訓練數據的自動生成，以及從海量非高質量數據中自動選擇可供學習的樣本；二是架構/算法自動化 ：實現網絡架構自構建和訓練算法自設計。要能根據目標任務自動解析完成任務所需的“功能塊”，并以最優方式加以組裝（以盡可能簡約，甚至極簡的方式）形成所需的深度網絡架構；三是應用/更新自動化 ：要實現損失度量隨問題（數據）的自適應設定和正則項的自適應設定，實現網絡訓練算法的自適應構建和選擇；實現任務自切換和環境自適應。要實現一個架構完成多項任務、自動切換的機器學習, 要能夠持續學習、自主進化、自適應地去完成新任務。

我們把能實現上述六個“自動化”目標的機器學習稱為“自動化機器學習”。顯然，我們現在仍處于機器學習的人工化階段，但正在走向自動化、自主化階段。應該高度認識實現機器學習自動化的重大意義與價值，筆者認為，它既是實現自主智能的必經之路，也是推動人工智能發展、應用的現實需求。

如何實現機器學習自動化：SLeM框架

如何實現機器學習自動化？表面上看，它涉及機器學習的各個要素（例如：假設空間、損失函數、正則項、學習算法等）的設計問題，但本質上涉及的是學習方法論的學習問題。這里提出一種模擬學習方法論(Simulate Learning Methodology，SLeM)的框架，如圖5所示，并闡述如何通過SLeM來實現機器學習自動化。

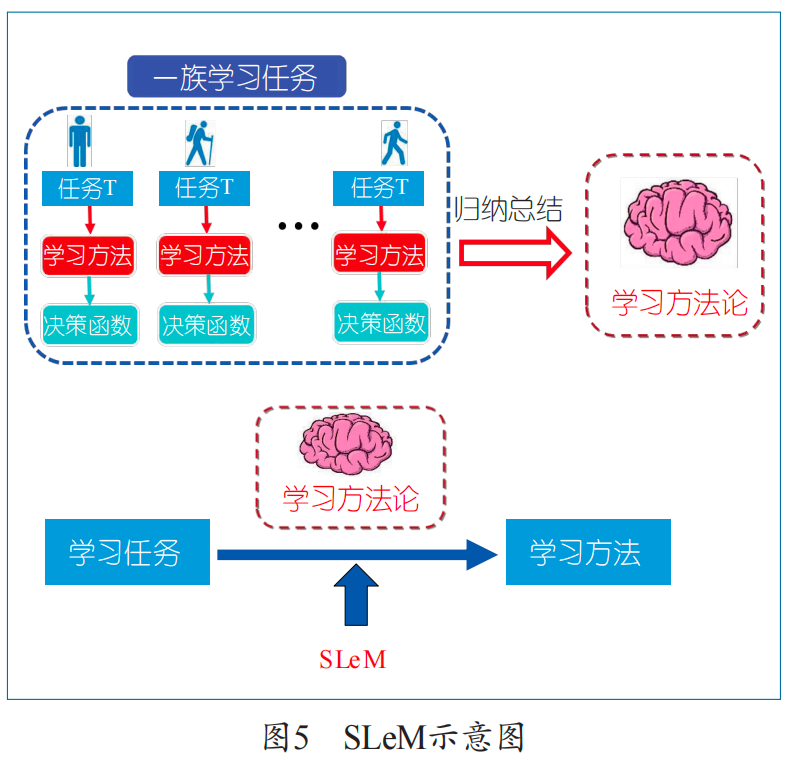
學習方法論是指導、管理學習者如何去學習的一般原則與方法學。為建立SLeM框架，我們需要先嚴格地從數學上定義學習任務、學習方法、學習方法論等概念。

學習任務

學習的目的是對可觀測的現實世界規律作總結和刻畫。我們認為，一個現實世界的規律可以用一個隨機變量來描述，或等價地，由一個分布函數（密度函數）來描述。一個隨機變量（現實世界規律）在不同時空的抽樣即表現為不同時空反映同一規律的數據（這些構成通常機器學習研究的對象）。從數據中學習，可以表現為分類、回歸、降維、隱變量識別等具體任務，但本質上是學習數據背后的分布（只要知道了分布，所有具體任務都能通過分布函數表示出來）。因此，學習任務宜定義作統計上的“密度估計問題”，即根據給定的數據，確定數據背后的隨機變量分布（密度函數）問題。學習的本質是對一個可觀測的現實世界規律作總結和刻畫。

學習方法

依據前文對機器學習要素的分析，只要指定一組特定的“數據產生方法、假設空間/機器架構、損失度量、優化算法”，就可以認為定義了一個學習方法。由此，我們定義一個學習方法是對學習空間的一組指定K=(D, f, L, A)，其中D是數據生成方法，f是機器架構，L是損失度量，A是一個可用以訓練的優化算法。這里學習空間K自然定義為分布函數空間、假設空間、損失函數空間、優化算法空間的乘積，如圖6所示。

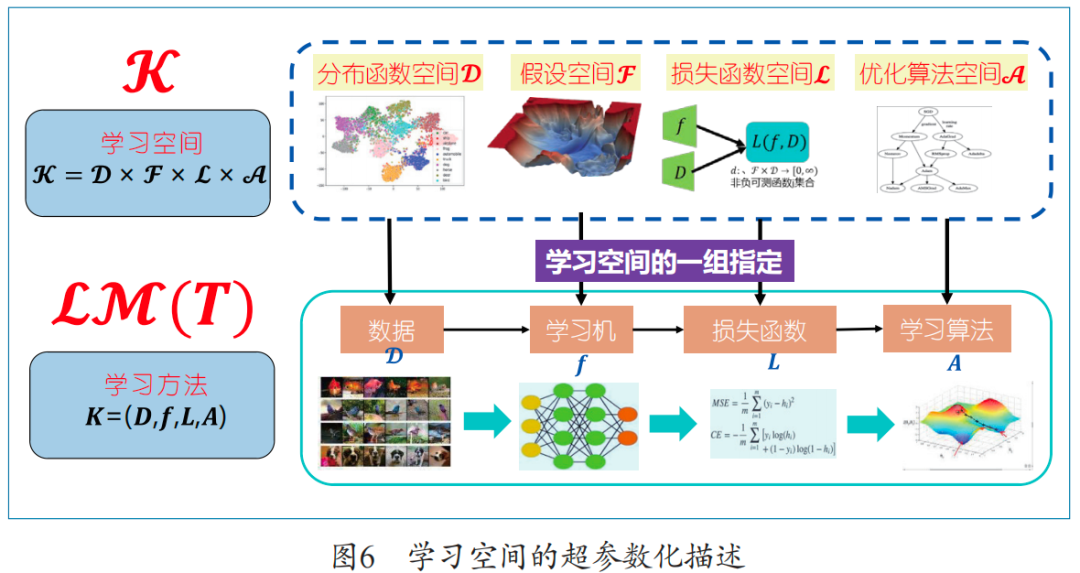
學習空間K顯然是無窮維的。但如果我們假設：K的每一因子空間都存在可數基底（應用中自然滿足，例如，不同均值與方差的高斯分布構成分布函數空間的可數基底），則學習空間K便可以序列化（即同構于序列空間），即對應地能用4個無窮序列來描述。這個過程被稱為學習空間的超參數化。如此一來，學習方法便可以表示為4個無窮序列，或進而將無窮維序列有限維截斷，近似表示為4個有窮序列。這樣參數化后，一個學習方法便可被描述為4個有限參數序列。

學習方法論

有了以上準備，我們將學習方法論定義為：從任務空間到學習空間的一個映照（可記為LM）。更具體地，給定一個任務T，LM(T)是在學習空間的一個取值，它由4元組描述，對應數據產生方法、假設空間/機器架構、損失度量和優化算法的參數化表示。這就是學習方法論。學習方法論本質上是函數空間上的一個映射，是參數的一個賦值規則。顯然，SLeM是函數空間上的函數逼近問題。

融合SLeM的問題求解過程如圖7所示。

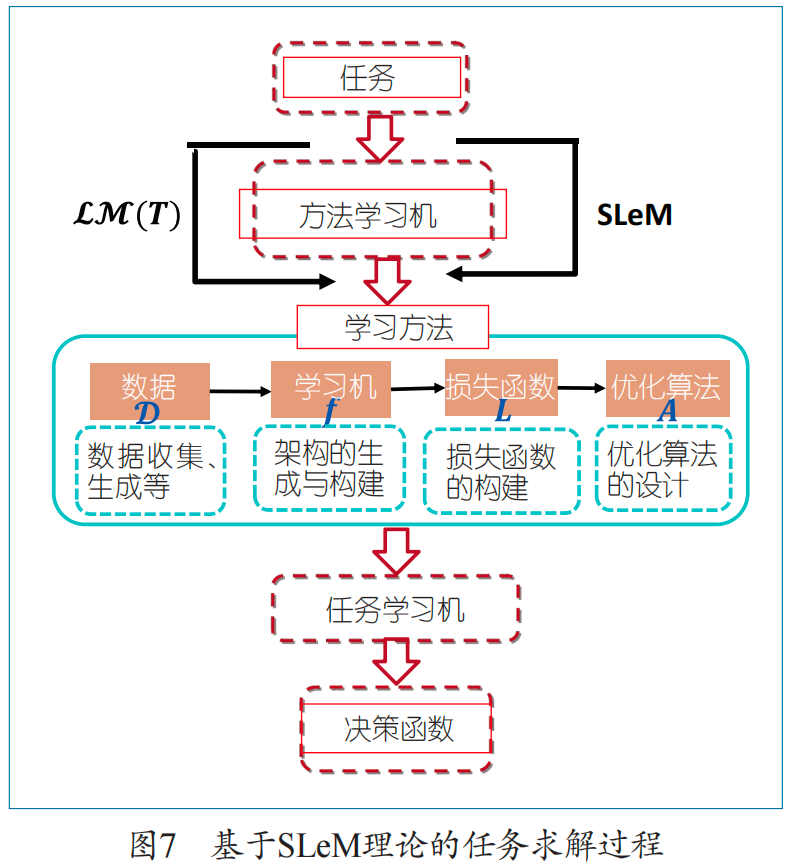
不同于傳統的機器學習過程（給定數據、機器架構，選擇一個優化算法去求解，得到決策函數），基于SLeM求解問題，是在傳統的機器學習之前增加了一步方法論學習，然后根據方法論學習機設計的方法去執行機器學習任務。因此，它是從任務出發，先產生方法，再執行任務，是一個典型的兩階段任務求解過程。

基于元數據的SLeM計算模型

SLeM可以描述成函數空間上的一個標準機器學習問題。但這種模型只有理論上的意義。然而，如果我們給出一些假設，就能將這樣的機器學習模型變成一個計算機可操作的模型。例如，如果假設學習方法論的好壞可以通過一組元數據來評判（類似于通過學生的考試成績度量老師的教學表現, 這里元數據可以類比為檢驗學生成績的一組標準考題），則SLeM模型可變成一個可操作的兩階段優化模型，它們能夠非常方便的用計算機處理。進而，如果把度量方法論優劣的元數據換成元知識，即基于規則來評判方法論，則可以獲得另一類型的雙層優化SLeM模型，即基于元知識的SLeM模型。總之，基于對方法論的不同評價標準，可獲得不同的SLeM計算模型。

SLeM框架與其他框架的比較

基于SLeM的一般問題求解是從任務出發，根據任務產生方法，然后再去完成任務。整個求解過程可以分為“方法學習”和“任務學習”兩個階段。顯然，這和現在的機器學習不同，這兩者泛化的目標不一樣，輸入、結構、模型也都不一樣。SLeM框架與元學習也非常不一樣，元學習包括很多演化過程，但總體上都是啟發式的，還沒有明確的數學模型。

SLeM應用舉例

遷移學習理論

我們首先應用SLeM理論解決遷移學習的度量問題。我們知道, 人工智能的目標是遷移學習，但是目前的遷移學習一直沒有很好的理論支撐。利用SLeM理論，我們可以證明：從完成一些任務中學到的知識能不能遷移，取決于三個基本要素。一是我們過去是否見過這個任務，即任務的相關性。二是任務機和學習機的空間復雜性。三是我們用于度量方法論的元數據和訓練數據的一致性。這三條要素的發現說明了遷移學習理論構建的可能性。

機器學習自動化

接下來展示如何用SLeM理論解決機器學習自動化的問題。首先要考慮數據自動化：通過給每一個數據賦權的方法來參數化，運用SLeM模型自動地從大量數據中選擇適用于網絡訓練的數據（即數據自選擇）。我們提出了一個名為Class-aware Meta-Weight-Net的方法論學習機。應用展示，基于SLeM選擇后的數據學習效果遠遠優于不選擇、人工選擇或隨機選擇數據集的學習效果，并且基于SLeM的方法對非均衡、高噪音數據集可用。該方法在粵港澳大灣區算法大賽（2022）中獲得冠軍。SLeM也被用來做標簽的自矯正，即對標記錯誤的數據進行自動校正，從而解決半監督學習所得的標簽的校正問題。關于網絡自動化方面，我們嘗試了在深度學習中自動嵌入變換問題，取得到非常好的效果。利用SLeM理論也可以進行度量自動化學習，換句話說，就是自適應設定與任務相關的損失度量。我們提出了一個Meta Loss Adjuster方法論學習網絡，取得了不錯的學習效果。最后我們將SLeM用于算法自動化，特別地，應用SLeM學習如何自動設置BP算法的學習率。為此，我們設計了一個稱作Meta-LR-Schedule-Net的方法論網絡。測試表明，耦合Meta-LR-Schedule-Net的深度學習平均提高深度學習泛化性能4%左右。

總的來說，通過構建SLeM方法機，可以學習具有明確物理意義的超參賦值學習方法，實現面向不同任務的機器學習自動化任務。筆者團隊已將所有研究成果公開在開源平臺上，參見https://github.com/xjtushujun/Auto-6ML。

總結與展望

人工智能的當前應用仍以“帶先驗假設的機器學習”和人工化為特征，下一步發展必然會以“實現機器學習自動化”為追求，這是機器學習發展的根本問題。實現機器學習自動化要求對數據、網絡、損失、算法、任務等要素進行設計和調控。實現這一目標要求“任務到方法的映射”，即學習方法論的學習（SLeM），現有研究/方法尚不能支持這一目標的實現。筆者團隊提出了SLeM的數學框架、嚴格定義、數學模型、一般算法，展示了如何用SLeM方法解決機器學習自動化問題。SLeM為機器學習自動化研究提供了一個形式化/模型化/科學化的研究框架和途徑。已有應用表明SLeM是一個強大而有效的工具。應用SLeM的關鍵在學習空間的超參數化方案和方法學習機的設計上。另外，元數據集的選擇是決定SLeM效果的關鍵要素。SLeM正在快速發展中，我們期待它的持續深化、拓廣和工具化。

（本文根據CNCC2022特邀報告整理而成）

作者：

徐宗本

西安交通大學數學與統計學院教授。中國科學院院士。主要研究方向為智能信息處理、機器學習、數據建模基礎理論。

zbxu@mail.xjtu.edu.cn

整理：

劉克彬?

CCF專業會員。清華大學副研究員。主要研究方向為物聯網和普適計算。

kebinliu2021@mail.tsinghua.edu.cn

朱追

CCF學生會員。清華大學自動化系博士研究生。主要研究方向為邊緣智能與物聯網。

z-zhu22@mails.tsinghua.edu.cn

編輯：黃飛

?