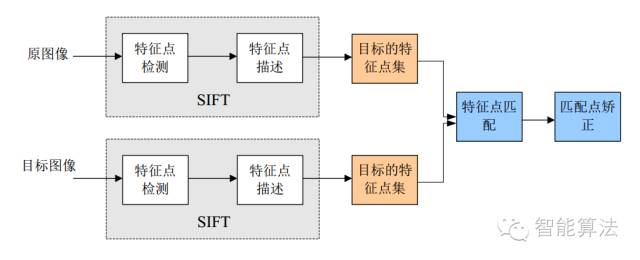
一. SIFT簡介
1.1 算法提出的背景:
成像匹配的核心問題是將同一目標在不同時間、不同分辨率、不同光照、不同位姿情況下所成的像相對應。傳統(tǒng)的匹配算法往往是直接提取角點或邊緣,對環(huán)境的適應能力較差,急需提出一種魯棒性強、能夠適應不同光照、不同位姿等情況下能夠有效識別目標的方法。1999年British Columbia大學大衛(wèi).勞伊( David G.Lowe)教授總結(jié)了現(xiàn)有的基于不變量技術的特征檢測方法,并正式提出了一種基于尺度空間的、對圖像縮放、旋轉(zhuǎn)甚至仿射變換保持不變性的圖像局部特征描述算子-SIFT(尺度不變特征變換),這種算法在2004年被加以完善。
1.2 算法思想:
將一幅圖像映射(變換)為一個局部特征向量集;特征向量具有平移、縮放、旋轉(zhuǎn)不變性,同時對光照變化、仿射及投影變換也有一定不變性。
算法實現(xiàn)步驟簡述:
SIFT算法的實質(zhì)可以歸為在不同尺度空間上查找特征點(關鍵點)的問題。
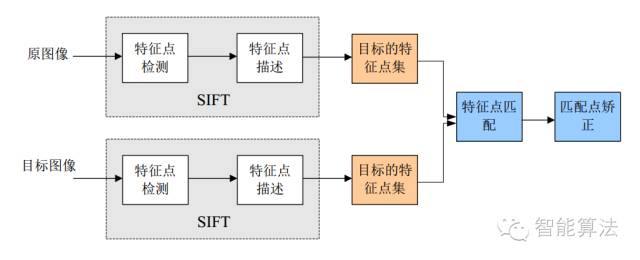
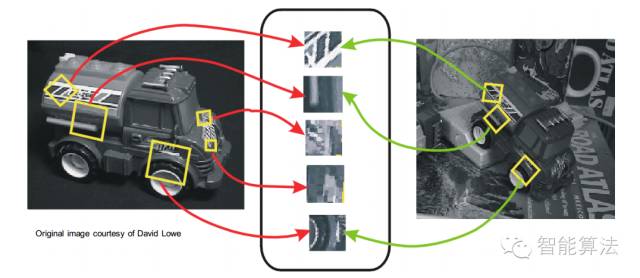
1.3 SIFT算法實現(xiàn)物體識別主要有三大工序:
1、提取關鍵點;?
2、對關鍵點附加詳細的信息(局部特征)也就是所謂的描述器;
3、通過兩方特征點(附帶上特征向量的關鍵點)的兩兩比較找出相互匹配的若干對特征點,也就建立了景物間的對應關系。
二. SIFT算法實現(xiàn)細節(jié)
2.1. 構(gòu)建尺度空間
尺度空間理論基礎:
這是一個初始化操作,尺度空間理論目的是模擬圖像數(shù)據(jù)的多尺度特征。高斯核是唯一可以產(chǎn)生多尺度空間的核,一個圖像的尺度空間, L( x,y,σ) ,定義為原始圖像I(x,y)與一個可變尺度的2維高斯函數(shù)G(x,y,σ) 卷積運算。尺度是自然存在的,不是人為創(chuàng)造的!高斯卷積只是表現(xiàn)尺度空間的一種形式…
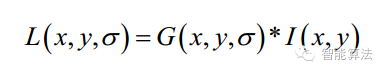
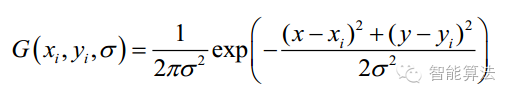
其中 G(x,y,σ) 是尺度可變高斯函數(shù)(x,y)是空間坐標,是尺度坐標。σ大小決定圖像的平滑程度,大尺度對應圖像的概貌特征,小尺度對應圖像的細節(jié)特征。大的σ值對應粗糙尺度(低分辨率),反之,對應精細尺度(高分辨率)。為了有效的在尺度空間檢測到穩(wěn)定的關鍵點,提出了高斯差分尺度空間(DOG scale-space)。利用不同尺度的高斯差分核與圖像卷積生成。
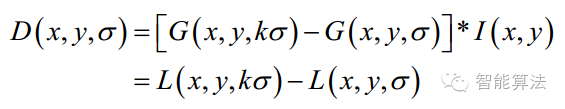
下圖所示不同σ下圖像尺度空間:
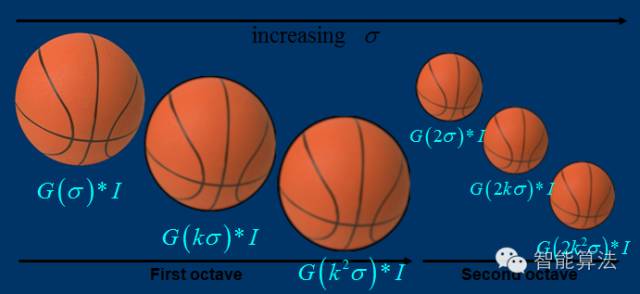
關于尺度空間的理解說明:
2kσ中的2是必須的,尺度空間是連續(xù)的。在 Lowe的論文中 ,將第0層的初始尺度定為1.6(最模糊),圖片的初始尺度定為0.5(最清晰). 在檢測極值點前對原始圖像的高斯平滑以致圖像丟失高頻信息,所以 Lowe 建議在建立尺度空間前首先對原始圖像長寬擴展一倍,以保留原始圖像信息,增加特征點數(shù)量。尺度越大圖像越模糊。
圖像金字塔的建立:
對于一幅圖像I,建立其在不同尺度(scale)的圖像,也成為子八度(octave),這是為了scale-invariant,也就是在任何尺度都能夠有對應的特征點,第一個子八度的scale為原圖大小,后面每個octave為上一個octave降采樣的結(jié)果,即原圖的1/4(長寬分別減半),構(gòu)成下一個子八度(高一層金字塔)。
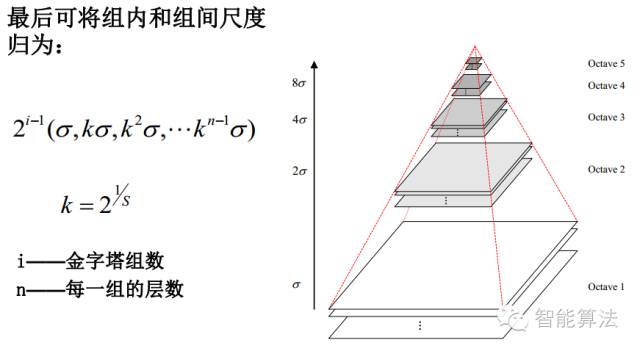
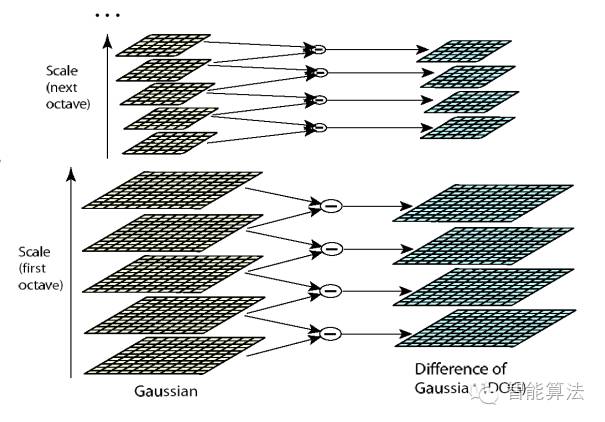
由圖片size決定建幾個塔,每塔幾層圖像(S一般為3-5層)。0塔的第0層是原始圖像(或你double后的圖像),往上每一層是對其下一層進行Laplacian變換(高斯卷積,其中σ值漸大,例如可以是σ, k*σ, k*k*σ…),直觀上看來越往上圖片越模糊。塔間的圖片是降采樣關系,例如1塔的第0層可以由0塔的第3層down sample得到,然后進行與0塔類似的高斯卷積操作。
2.2.?關鍵點檢測
為了尋找尺度空間的極值點,每一個采樣點要和它所有的相鄰點比較,看其是否比它的圖像域和尺度域的相鄰點大或者小。如圖所示,中間的檢測點和它同尺度的8個相鄰點和上下相鄰尺度對應的9×2個點共26個點比較,以確保在尺度空間和二維圖像空間都檢測到極值點。一個點如果在DOG尺度空間本層以及上下兩層的26個領域中是最大或最小值時,就認為該點是圖像在該尺度下的一個特征點,如圖所示。
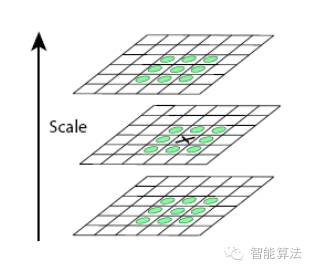
同一組中的相鄰尺度(由于k的取值關系,肯定是上下層)之間進行尋找,在極值比較的過程中,每一組圖像的首末兩層是無法進行極值比較的,為了滿足尺度變化的連續(xù)性,我們在每一組圖像的頂層繼續(xù)用高斯模糊生成了3幅圖像,高斯金字塔有每組S+3層圖像。DOG金字塔每組有S+2層圖像。下圖中s=3
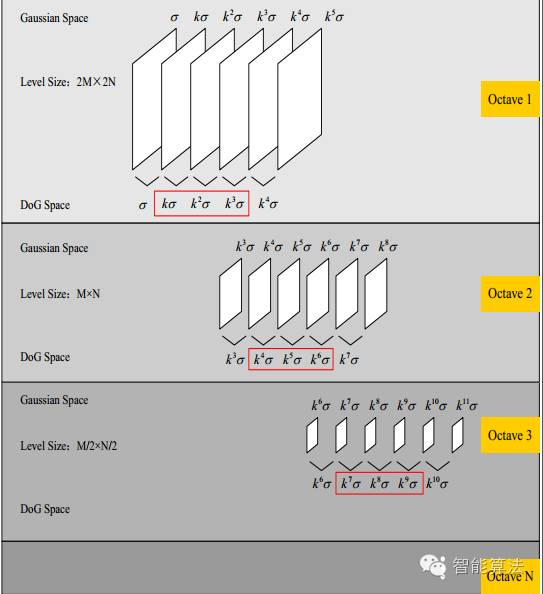
這里解釋下尺度變化的連續(xù)性:
假設s=3,也就是每個塔里有3層,則k=21/s=21/3,那么按照上圖可得Gauss Space和DoG space 分別有3個(s個)和2個(s-1個)分量,在DoG space中,1st-octave兩項分別是σ,kσ; 2nd-octave兩項分別是2σ,2kσ;由于無法比較極值,我們必須在高斯空間繼續(xù)添加高斯模糊項,使得形成σ,kσ,k2σ,k3σ,k4σ這樣就可以選擇DoG space中的中間三項kσ,k2σ,k3σ(只有左右都有才能有極值),那么下一octave中(由上一層降采樣獲得)所得三項即為2kσ,2k2σ,2k3σ,其首項2kσ=24/3。剛好與上一octave末項k3σ=23/3尺度變化連續(xù)起來,所以每次要在Gaussian space添加3項,每組(塔)共S+3層圖像,相應的DoG金字塔有S+2層圖像。
2.3.?消除錯配點
由于DoG值對噪聲和邊緣較敏感,因此,在上面DoG尺度空間中檢測到局部極值點還要經(jīng)過進一步的檢驗才能精確定位為特征點。為了提高關鍵點的穩(wěn)定性,需要對尺度空間DoG函數(shù)進行曲線擬合。利用DoG函數(shù)在尺度空間的Taylor展開式:
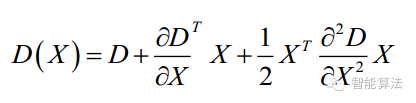
對上式求導,并令其為0,得到精確的位置, 得
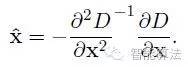
在已經(jīng)檢測到的特征點中,要去掉低對比度的特征點和不穩(wěn)定的邊緣響應點。去除低對比度的點:把上式代入其中,即在DoG Space的極值點處D(x)取值,只取前兩項可得:
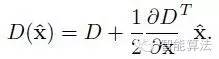
若 ?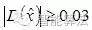 ,該特征點就保留下來,否則丟棄。
,該特征點就保留下來,否則丟棄。
邊緣響應的去除
一個定義不好的高斯差分算子的極值在橫跨邊緣的地方有較大的主曲率,而在垂直邊緣的方向有較小的主曲率。主曲率通過一個2×2 的Hessian矩陣H求出:
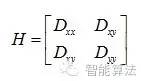
導數(shù)由采樣點相鄰差估計得到。D的主曲率和H的特征值成正比,令α為較大特征值,β為較小的特征值,則
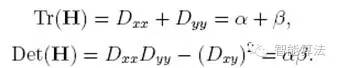
令α=γβ,則
(r + 1)2/r的值在兩個特征值相等的時候最小,隨著r的增大而增大,因此,為了檢測主曲率是否在某域值r下,只需檢測
if (α+β)/ αβ> (r+1)2/r, throw it out. ? 在Lowe的文章中,取r=10。
2.4.?關鍵點描述
上一步中確定了每幅圖中的特征點,為每個特征點計算一個方向,依照這個方向做進一步的計算,?利用關鍵點鄰域像素的梯度方向分布特性為每個關鍵點指定方向參數(shù),使算子具備旋轉(zhuǎn)不變性。
為(x,y)處梯度的模值和方向公式。其中L所用的尺度為每個關鍵點各自所在的尺度。至此,圖像的關鍵點已經(jīng)檢測完畢,每個關鍵點有三個信息:位置,所處尺度、方向,由此可以確定一個SIFT特征區(qū)域。
梯度直方圖的范圍是0~360度,其中每10度一個柱,總共36個柱。隨著距中心點越遠的領域其對直方圖的貢獻也響應減小.Lowe論文中還提到要使用高斯函數(shù)對直方圖進行平滑,減少突變的影響。
在實際計算時,我們在以關鍵點為中心的鄰域窗口內(nèi)采樣,并用直方圖統(tǒng)計鄰域像素的梯度方向。梯度直方圖的范圍是0~360度,其中每45度一個柱,總共8個柱, 或者每10度一個柱,總共36個柱。Lowe論文中還提到要使用高斯函數(shù)對直方圖進行平滑,減少突變的影響。直方圖的峰值則代表了該關鍵點處鄰域梯度的主方向,即作為該關鍵點的方向。
直方圖中的峰值就是主方向,其他的達到最大值80%的方向可作為輔助方向,通過對關鍵點周圍圖像區(qū)域分塊,計算塊內(nèi)梯度直方圖,生成具有獨特性的向量,這個向量是該區(qū)域圖像信息的一種抽象,具有唯一性。首先將坐標軸旋轉(zhuǎn)為關鍵點的方向,以確保旋轉(zhuǎn)不變性。以關鍵點為中心取8×8的窗口。
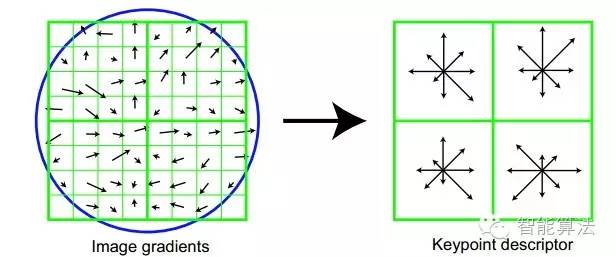
16*16的圖中其中1/4的特征點梯度方向及scale,右圖為其加權(quán)到8個主方向后的效果。圖左部分的中央為當前關鍵點的位置,每個小格代表關鍵點鄰域所在尺度空間的一個像素,利用公式求得每個像素的梯度幅值與梯度方向,箭頭方向代表該像素的梯度方向,箭頭長度代表梯度模值,然后用高斯窗口對其進行加權(quán)運算。
圖中藍色的圈代表高斯加權(quán)的范圍(越靠近關鍵點的像素梯度方向信息貢獻越大)。然后在每4×4的小塊上計算8個方向的梯度方向直方圖,繪制每個梯度方向的累加值,即可形成一個種子點,如圖右部分示。此圖中一個關鍵點由2×2共4個種子點組成,每個種子點有8個方向向量信息。這種鄰域方向性信息聯(lián)合的思想增強了算法抗噪聲的能力,同時對于含有定位誤差的特征匹配也提供了較好的容錯性。
計算keypoint周圍的16*16的window中每一個像素的梯度,而且使用高斯下降函數(shù)降低遠離中心的權(quán)重。
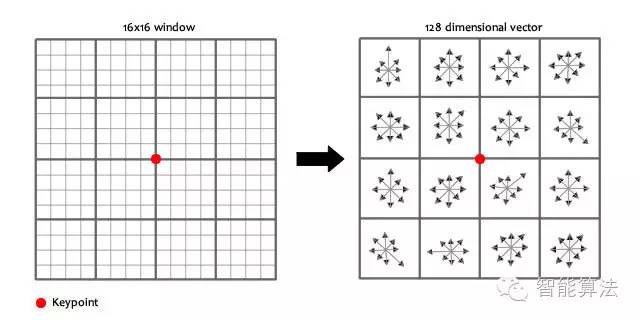
在每個4*4的1/16象限中,通過加權(quán)梯度值加到直方圖8個方向區(qū)間中的一個,計算出一個梯度方向直方圖。這樣就可以對每個feature形成一個4*4*8=128維的描述子,每一維都可以表示4*4個格子中一個的scale/orientation. 將這個向量歸一化之后,就進一步去除了光照的影響。
2.5.?關鍵點匹配
生成了A、B兩幅圖的描述子,(分別是k1*128維和k2*128維),就將兩圖中各個scale(所有scale)的描述子進行匹配,匹配上128維即可表示兩個特征點match上了。
實際計算過程中,為了增強匹配的穩(wěn)健性,Lowe建議對每個關鍵點使用4×4共16個種子點來描述,這樣對于一個關鍵點就可以產(chǎn)生128個數(shù)據(jù),即最終形成128維的SIFT特征向量。此時SIFT特征向量已經(jīng)去除了尺度變化、旋轉(zhuǎn)等幾何變形因素的影響,再繼續(xù)將特征向量的長度歸一化,則可以進一步去除光照變化的影響。當兩幅圖像的SIFT特征向量生成后,下一步我們采用關鍵點特征向量的歐式距離來作為兩幅圖像中關鍵點的相似性判定度量。取圖像1中的某個關鍵點,并找出其與圖像2中歐式距離最近的前兩個關鍵點,在這兩個關鍵點中,如果最近的距離除以次近的距離少于某個比例閾值,則接受這一對匹配點。降低這個比例閾值,SIFT匹配點數(shù)目會減少,但更加穩(wěn)定。
為了排除因為圖像遮擋和背景混亂而產(chǎn)生的無匹配關系的關鍵點,Lowe提出了比較最近鄰距離與次近鄰距離的方法,距離比率ratio小于某個閾值的認為是正確匹配。因為對于錯誤匹配,由于特征空間的高維性,相似的距離可能有大量其他的錯誤匹配,從而它的ratio值比較高。Lowe推薦ratio的閾值為0.8。但作者對大量任意存在尺度、旋轉(zhuǎn)和亮度變化的兩幅圖片進行匹配,結(jié)果表明ratio取值在0. 4~0. 6之間最佳,小于0. 4的很少有匹配點,大于0. 6的則存在大量錯誤匹配點。(如果這個地方你要改進,最好給出一個匹配率和ration之間的關系圖,這樣才有說服力)作者建議ratio的取值原則如下:
ratio=0. 4 對于準確度要求高的匹配;
ratio=0. 6 對于匹配點數(shù)目要求比較多的匹配;
ratio=0. 5 一般情況下。
也可按如下原則:當最近鄰距離<200時ratio=0. 6,反之ratio=0. 4。ratio的取值策略能排分錯誤匹配點。
當兩幅圖像的SIFT特征向量生成后,下一步我們采用關鍵點特征向量的歐式距離來作為兩幅圖像中關鍵點的相似性判定度量。取圖像1中的某個關鍵點,并找出其與圖像2中歐式距離最近的前兩個關鍵點,在這兩個關鍵點中,如果最近的距離除以次近的距離少于某個比例閾值,則接受這一對匹配點。降低這個比例閾值,SIFT匹配點數(shù)目會減少,但更加穩(wěn)定。
編輯:黃飛
?
 電子發(fā)燒友App
電子發(fā)燒友App









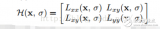

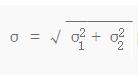











評論