我們現在有了很多非常厲害的深度學習框架,比如Tensorflow,CNTK,PaddlePaddle,Caffe2等等。然而,這些為了解決實際的應用問題而生的,而不是用來學習“深度學習”知識和思想的。所以微軟Xiaowuhu根據自己親身經歷的學習軌跡,歸納出了以下教程,可以幫助小白做到真正的從入門到精通。通過以下循序漸進地學習與動手實踐,一方面可以幫助讀者深刻理解“深度學習”的基礎知識,更好地理解并使用現有框架,另一方面可以助力讀者快速學習最新出現的各種神經網絡的擴展或者變型,跟上快速發展的AI浪潮。
寫在前面,為什么要出這個系列的教程呢?
總的說來,我們現在有了很多非常厲害的深度學習框架,比如Tensorflow,CNTK,PaddlePaddle,Caffe2等等。然而,我們用這些框架在搭建我們自己的深度學習模型的時候,到底做了一些什么樣的操作呢?我們試圖去閱讀框架的源碼來理解框架到底幫助我們做了些什么,但是……很難!很難!很難!因為深度學習是需要加速啦,分布式計算啦,框架做了很多很多的優化,也讓像我們這樣的小白難以理解這些框架的源碼。
這取決于你是想真正地掌握“深度學習”的思想,還是只想成為一個調參師?在我們看來,如TensorFlow,CNTK這些偉大的深度學習工具,是為了解決實際的應用問題而生的,而不是用來學習“深度學習”知識和思想的。所以我們根據自己親身經歷的學習軌跡,歸納出了以下教程,可以幫助小白做到真正的從入門到精通。
通過以下循序漸進地學習與動手實踐,一方面可以幫助讀者深刻理解“深度學習”的基礎知識,更好地理解并使用現有框架,另一方面可以助力讀者快速學習最新出現的各種神經網絡的擴展或者變型,跟上快速發展的AI浪潮。
對于這份教程的內容,如果沒有額外的說明,我們通常使用如下表格的命名約定:
?
| 符號 | 含義 |
|---|---|
| X | 輸入樣本 |
| Y | 輸入樣本的標簽 |
| Z | 線性運算的結果 |
| A | 激活函數/結果 |
| W | 權重矩陣 |
| B | 偏移矩陣 |
| J | 損失函數 |
| 大寫字母 | 矩陣或矢量,如A,W,B |
| 小寫字母 | 變量,標量,如a,w,b |
| x1,2 | 第1個樣本的第2個特征值 |
| wL2,3 | 第L層第2個神經元對第L-1層第3個神經元的權重值 |
| 矩陣的行 | 一批樣本的某一個特征值的集合 |
| 矩陣的列 | 一批樣本的某一個樣本的所有特征值 |
?
適用范圍
沒有各種基礎想學習卻無從下手哀聲嘆氣的玩家,請按時跟蹤最新博客,推導數學公式,跑通代碼,并及時提出問題,以求最高療效;
深度學習小白,有直觀的人工智能的認識,強烈的學習欲望和需求,請在博客的基礎上配合代碼食用,效果更佳;
調參師,訓練過模型,調過參數,想了解框架內各層運算過程,給玄學的調參之路添加一點心理保障;
超級高手,提出您寶貴的意見,給廣大初學者指出一條明路!
前期準備
環境:
Windows 10 version 1809
Visual Studio 2017 Community or above
Python 3.6.6
Jupyter Notebook (可選)
自己:
清醒的頭腦(困了的同學請自覺泡茶),紙和筆(如果想跟著推公式的話),鬧鐘(防止久坐按時起來轉轉),厚厚的衣服(有暖氣的同學請忽略)
網絡結構概覽
| 網絡結構名稱 | 網絡結構圖 | 應用領域 |
|---|---|---|
|
單入 單出 一層 |
? |
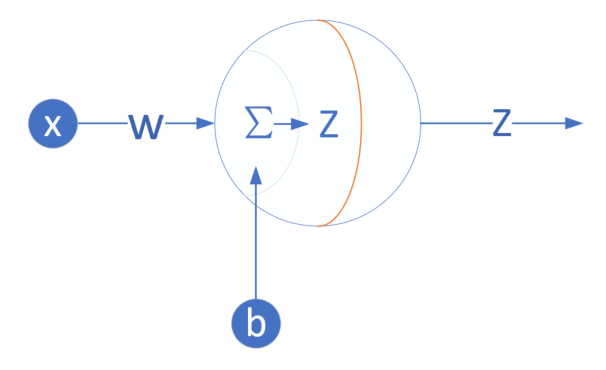
| ? | 一元線性回歸 |
|
多入 單出 一層 |
? |
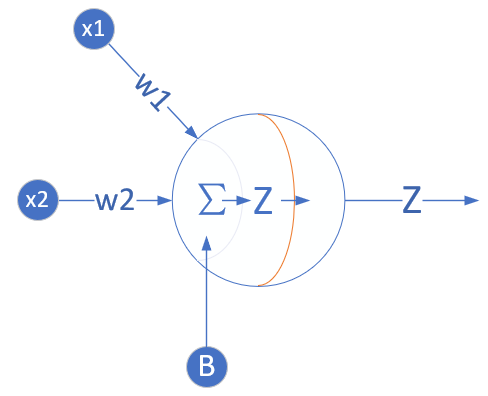
| ? | 多元線性回歸 |
|
多入 單出 一層 |
? |
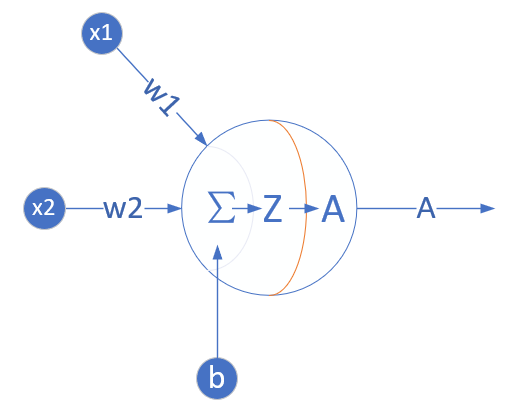
| ? | 線性二分類 |
|
多入 多出 一層 |
? |
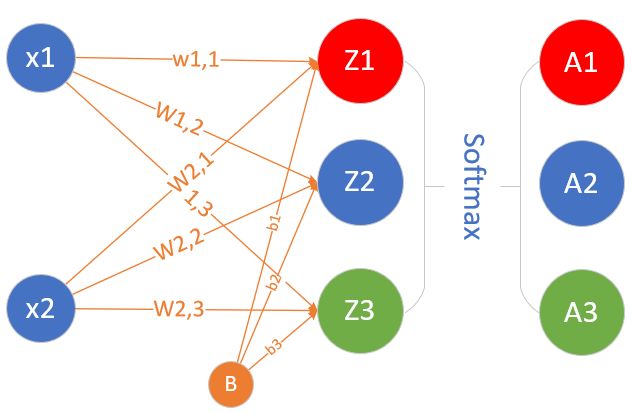
| ? | 線性多分類 |
|
單入 單出 兩層 |
? |
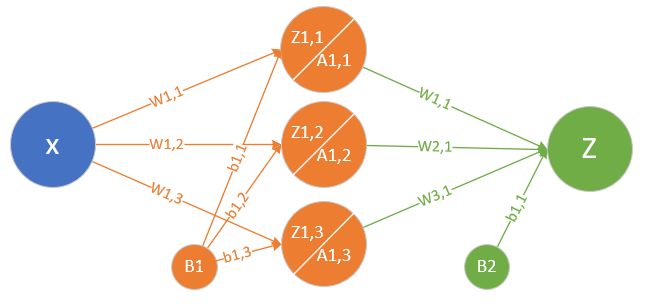
| ? |
一元非線性回歸/擬合 可以擬合任意復雜函數 |
|
多入 單出 兩層 |
? |
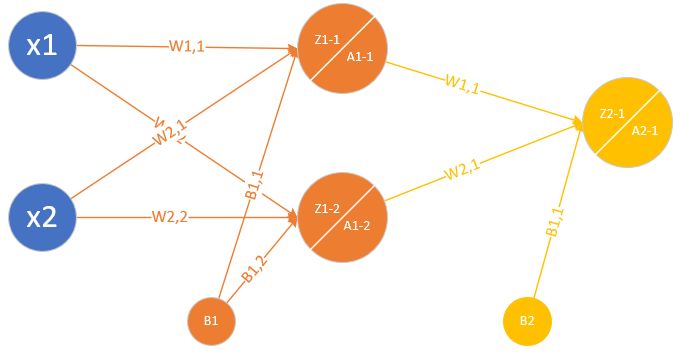
| ? | 非線性二分類 |
|
多入 多出 兩層 |
? |
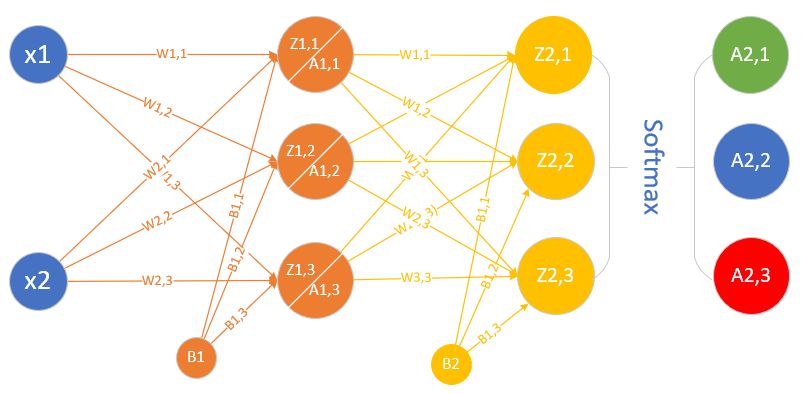
| ? | 非線性多分類 |
|
多入 多出 三層 |
? |

| ? | 非線性多分類 |
?
目錄
1. 基本概念
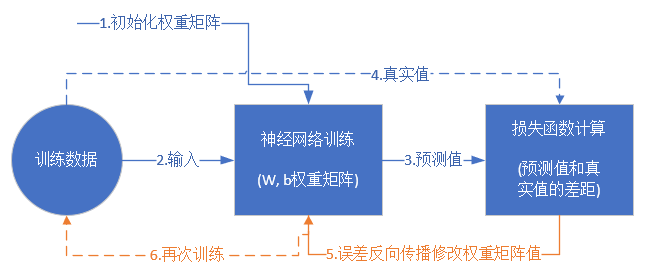
首先會講解一下神經網絡基本的訓練和工作原理,因為基本上各種教程里都沒有提到這一點,以至于筆者在剛開始學習神經網絡時一頭霧水,不得要領,不知從何處開始下手。
后面接的是導數公式和反向傳播公式,包括矩陣求導,這一部分可以大概瀏覽一下,主要的目的是備查,在自己推導反向公式時可以參考。
然后是反向傳播和梯度下降,我們先從簡單的線性方式說起(只有加法和乘法),而且用代入數值的方式來消除對公式的恐懼心理。然后會說到分層的復雜(非線性)函數的反向傳播,同樣用數值代入方式手推反向過程。
梯度下降是神經網絡的基本學習方法,我們會用單變量和雙變量兩種方式說明,配以可視化的圖解。再多的變量就無法用可視化方式來解釋了,所以我們力求用簡單的方式理解復雜的事物。
本部分最后是損失函數的講解,著重說明了神經網絡中目前最常用的均方差損失函數(用于回歸)和交叉熵損失函數(用于分類)。
2. 線性回歸
用線性回歸作為學習神經網絡的起點,是一個非常好的選擇,因為線性回歸問題本身比較容易理解,在它的基礎上,逐步的增加一些新的知識點,會形成一條比較平緩的學習曲線,或者說是邁向神經網絡的第一個小臺階。
單層的神經網絡,其實就是一個神經元,可以完成一些線性的工作,比如擬合一條直線,這用一個神經元就可以實現。當這個神經元只接收一個輸入時,就是單變量線性回歸,可以在二維平面上用可視化方法理解。當接收多個變量輸入時,叫做多變量線性回歸,此時可視化方法理解就比較困難了,通常我們會用變量兩兩組對的方式來表現。
當變量多于一個時,兩個變量的量綱和數值有可能差別很大,這種情況下,我們通常需要對樣本特征數據做歸一化,然后把數據喂給神經網絡進行訓練,否則會出現“消化不良”的情況。
3. 線性分類
分類問題在很多資料中都稱之為邏輯回歸,Logistic Regression,其原因是使用了線性回歸中的線性模型,加上一個Logistic二分類函數,共同構造了一個分類器。我們在本書中統稱之為分類。
神經網絡的一個重要功能就是分類,現實世界中的分類任務復雜多樣,但萬變不離其宗,我們都可以用同一種模式的神經網絡來處理。
本部分中,我們從最簡單的線性二分類開始學習,包括其原理,實現,訓練過程,推理過程等等,并且以可視化的方式來幫助大家更好地理解這些過程。
在第二步中,我們學習了實現邏輯非門,在本部分中,我們將利用學到的二分類知識,實現邏輯與門、與非門,或門,或非門。
做二分類時,我們一般用Sigmoid函數做分類函數,那么和Sigmoid函數長得特別像的雙曲正切函數能不能做分類函數呢?我們將會探索這件事情,從而對分類函數、損失函數、樣本標簽有更深的理解。
然后我們將進入線性多分類的學習。多分類時,可以一對一、一對多、多對多,那么神經網絡使用的是哪種方式呢?
Softmax函數是多分類問題的分類函數,通過對它的分析,我們學習多分類的原理、實現、以及可視化結果,從而理解神經網絡的工作方式。

4. 非線性回歸
從這一步開始,我們進入了兩層神經網絡的學習,從而解決非線性問題。
在兩層神經網絡之間,必須有激活函數連接,從而加入非線性因素,提高神經網絡的能力。所以,我們先從激活函數學起,一類是擠壓型的激活函數,常用于簡單網絡的學習;另一類是半線性的激活函數,常用于深度網絡的學習。
接下來我們將驗證著名的萬能近似定理,建立一個雙層的神經網絡,來擬合一個比較復雜的函數。
在上面的雙層神經網絡中,已經出現了很多的超參,都會影響到神經網絡的訓練結果。所以在完成了基本的擬合任務之后,我們將會嘗試著調試這些參數,得到更好的訓練效果(又快又好),從而得到超參調試的第一手經驗。
。

5. 非線性分類
我們在第三步中學習了線性分類,在本部分中,我們將學習更復雜的分類問題,比如,在很多年前,兩位著名的學者證明了感知機無法解決邏輯中的異或問題,從而使感知機這個研究領域陷入了長期的停滯。我們將會在使用雙層網絡解決異或問題。
異或問題是個簡單的二分類問題,因為畢竟只有4個樣本數據,我們會用更復雜的數據樣本來學習非線性多分類問題,并理解其工作原理。
然后我們將會用一個稍微復雜些的二分類例子,來說明在二維平面上,神經網絡是通過怎樣的神奇的線性變換加激活函數預算,把線性不可分的問題轉化為線性可分問題的。
解決完二分類問題,我們將學習如何解決更復雜的三分類問題,由于樣本的復雜性,必須在隱層使用多個神經元才能完成分類任務。
最后我們將搭建一個三層神經網絡,來解決MNIST手寫數字識別問題,并學習使用梯度檢查來幫助我們測試反向傳播代碼的正確性。
數據集的使用,是深度學習的一個基本技能,開發集、驗證集、測試集,合理地使用才能得到理想的泛化能力強的模型。
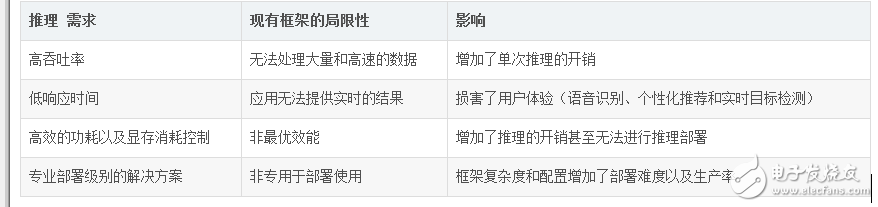
6. 模型推理與部署
我們已經用神經網絡訓練出來了一套權重矩陣,但是這個模型如何使用呢?我們總不能在實際生產環境中使用python代碼來做推理吧?更何況在手機中也是不能運行Python代碼的。
這就引出了模型的概念。一個模型會記錄神經網絡的計算圖,并加載權重矩陣,而這些模型會用C++等代碼來實現,以保證部署的便利。
我們將會學習到在Windows上使用ONNX模型的方法,然后是在Android上的模型部署方法。而在iOS設備上的模型,與Android的原理相同,有需要的話可以自己找資料學習。我們也許會考慮以后增加這部分內容。
7. 深度神經網絡
在前面的幾步中,我們用簡單的案例,逐步學習了眾多的知識,使得我們可以更輕松地接觸深度學習。
從這一部分開始,探討深度學習的一些細節,如權重矩陣初始化、梯度下降優化算法、批量歸一化等高級知識。
由于深度網絡的學習能力強的特點,會造成網絡對樣本數據過分擬合,從而造成泛化能力不足,因為我們需要一些手段來改善網絡的泛化能力。
8. 卷積神經網絡
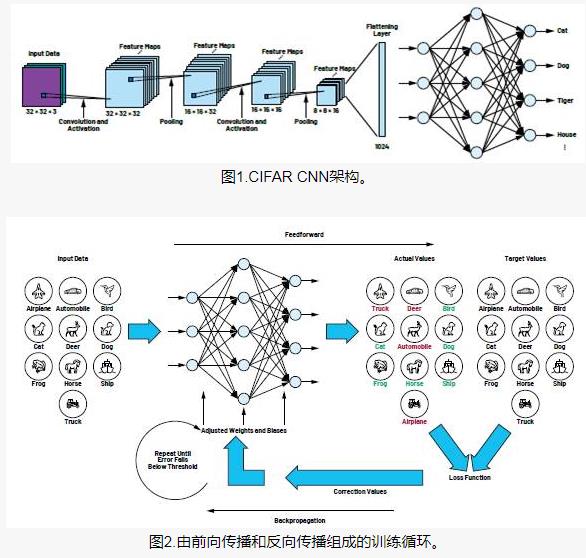
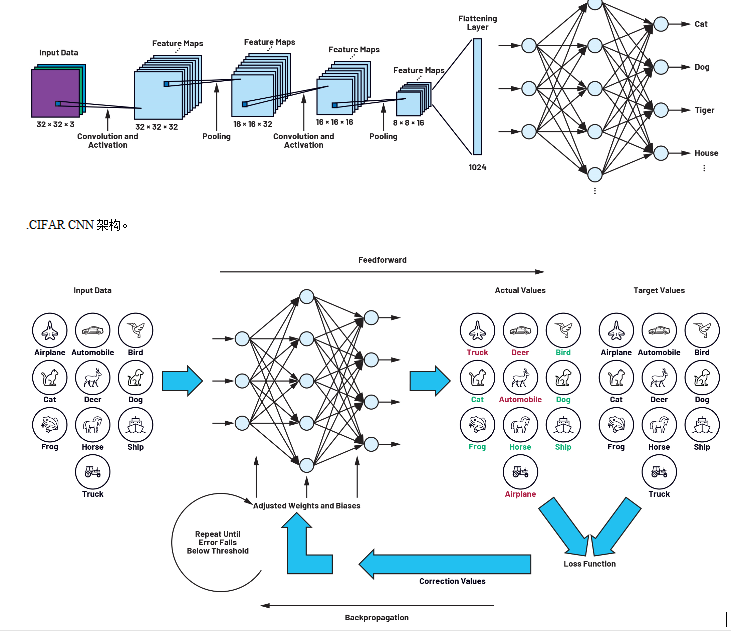
卷積神經網絡是深度學習中的一個里程碑式的技術,有了這個技術,才會讓計算機有能力理解圖片和視頻信息,才會有計算機視覺的眾多應用。
在本部分的學習中,我們將會逐步介紹卷積的前向計算、卷積的反向傳播、池化的前向計算與反向傳播,然后用代碼實現一個卷積網絡并訓練一些實際數據。
在后面我們還會介紹一些經典的卷積模型,向大師們學習一些解決問題的方法論問題。
編輯:黃飛
?
 電子發燒友App
電子發燒友App
























評論